混合周期维护平行机调度问题
2018-12-26程贞敏陈先康
程贞敏, 陈先康
(贵州大学 数学与统计学院, 贵阳 550025)
0 引 言
早在1974年, Baker[1]将调度问题定义为“完成若干项任务而对资源按时间进行分配的问题”,换句话说“调度问题是将资源分配给一定时间内不同任务,本质上是对任务合理地安排以达到某种条件下的最优结果的一个决策过程”[2]。
调度问题的研究在过去很长一段时间内都集中于经典调度问题的研究,也就是说通常考虑机器在加工的过程中不需要进行周期维护,但在现实生活中的情况往往比较复杂,有时就要求考虑机器维护的问题。关于机器维护的问题过去也有很多学者研究过。2007年, Ji[3]等讨论了带周期性维护且目标函数为最小化时间表长的单机排序问题,并证明了经典LPT算法的最坏情况界为2,且该问题不存在最坏情况界小于2的多项式时间算法。同年,宣竞[4]讨论了带周期性维护时间的平行机排序问题,并证明了P1|periodic-maintenance|Cmax在线情况的最优算法,算法竞争比为2。2012年,乔钰[5]讨论了机器具有不可用区间的平行机排序问题,其中第1台机器上有一段不可用区间,而第2台机器可以连续使用,工件在加工过程中不可以中断,目标函数为极小化时间表长。 乔钰在文中给出了精确算法和FPTAS算法来解决这个问题,并证明FPTAS算法的时间复杂性是o(n4/ε3)。2014年,Yu等[6]考虑了具有周期维护和不可中断的单机调度问题,目标函数是最小化时间表长,结果表明经典的列表算法(LS)、最长时间表长优先算法(LPT)和改进的最长时间优先算法(MLPT)算法对于所考虑的问题都具有相同的最坏情况比和相同的计算复杂度。2015年,王婷[7]研究了一个带有工具更换和固定周期维护的混合型平行机最小化时间表长调度问题,最后给出了一个基于经典的LPT算法的启发式算法LPTP和一个基于经典的LS算法的启发式算法LSP。2016年,Xu等[8]研究了具有固定维修周期或柔性维修周期的预防性维修的单机调度问题,生产计划中的2个共同目标最小化时间表长和总流程时间都被用来评估生产和维护计划的集成。根据装箱问题,给出了2种方案和2种目标的4种配方。
类似的研究[9-12]近几年也是愈来愈多,不过从上面可以看出,都只是基于机器有限的情况作出分析,甚至有的假设工件的数量小于机器的数量,或者是简单的给出了一个下界等。本研究主要考虑了部分机器需要维护,工件加工时间相同且不允许中断,同时工件数量严格大于机器数量,目标函数为最小化时间表长的调度问题。这对于一些车间甚至是企业在预先判断交货时间方面有着重要的理论意义。
1 问题描述
有m台机器,其中有m1台机器需要周期维护,而余下的m-m1台机器不需要周期维护,不失一般性,不妨设机器M1,M2,…,Mm1需要周期维护,各自的维护周期相同且记为T,维护时长也相同记为w,而机器Mm1+1,…,Mm不需要周期维护,现将n(n>m)个加工时长都为p的工件放在m台机器上加工,工件在加工的过程中不可以中断,目标函数是最小化时间表长。
上述调度问题用三元法[13]表示为Pm,Pm1PM|pj=p|Cmax,其中Pm1PM表示有m1台机器需要周期维护。工件加工需满足如下条件:
1)n>m,即工件的个数严格多于机器的台数;
2) 同一时刻,每个工件最多在一台机器上加工且一台机器最多加工一个工件;
3) 所有的工件在零时刻是随时准备加工的。

2 根据维护机器数量的不同将调度问题分3种情况讨论
2.1 设m台机器中没有机器需要维护
当m台机器中没有机器需要维护时,即m1=0,则调度问题Pm,Pm1PM|pj=p|Cmax就转化为经典的调度问题Pm|pj=p|Cmax[14],对于m1=0的情况有如下的算法:
算法1
步骤2 把n个任务按任意顺序排成一列,将这一列分为m部分,当1≤i≤n-zm时,第i部分为[(i-1)(z+1)p,i(z+1)p];当n-zm+1≤i≤m时,第i部分为[(i-1)zp+(n-zm)p,izp+(n-zm)p],转入步骤4。
步骤3 把n个任务按任意顺序排成一列,将这一列平均分为m部分,即第(1≤i≤m)部分为[(i-1)zp,izp],转入步骤4。
步骤4 把第i(其中i=1,…,m)部分放在处理机Pi上加工直至完成。


2.2 设m台机器中有部分机器需要进行周期维护
当m台机器中有部分机器需要周期维护时,有0 根据最优调度中最后一个工件的完工时刻是否在机器的维护时间段内,可以将问题分作2类,当最后一个工件的完工时刻在非维护段时记为类型Ⅰ,当最后一个工件的完工时刻在维护段时记为类型Ⅱ。 对于类型Ⅰ,k满足以下不等式: 化简有 最终得到对应类型Ⅰ关于k的不等式为 (1) 对于类型Ⅱ,k满足以下不等式: 化简有 最终得到对应类型Ⅱ关于k的不等式为 (2) 定理2 满足不等式(1)或者不等式(2)的正整数k如果存在,则k是唯一的。反之,给定一组加工时间相等的工件和一组部分需要维护的机器,则工件在机器上加工的最优时间表长Cmax一定满足类型Ⅰ和类型Ⅱ中的一种,并且对应于类型Ⅰ或者类型Ⅱ的正整数k是唯一的。 对于类型Ⅰ,根据最后的最优时间表长Cmax是否处于维护机器又可细分为2种情况,记最后一个工件在维护机器上加工时为情况一,最后一个工件在非维护机器上加工时为情况二。另外记k1为所有需周期维护的机器中在最后一个非维护时间段上加工工件数量最多的个数,k2为所有非维护机器中加工完所有工件时加工工件最多的个数。 对于类型Ⅰ中最后一个工件在维护机器上加工时有下面的不等式 化简有 即 (3) 另外对于类型Ⅰ中最后一个工件在维护机器上加工时还应满足 0 进一步化简得 -k(T+w) (4) 由式(3)和式(4)得到关于k1的不等式有 (5) 和k一样,如果这样的k1存在,则k1是唯一的,由于工件在加工过程中不可中断,则k1都只能取正整数,而且关于k1的不等式(5)右边与左边之差小于1,所以k1是唯一的。 对于k2由不等式(4)则有 (6) 同理k2也只能取正整数,并且如果这样的k2存在则由不等式(6)知k2是唯一的。 归纳上述推理,最终得到一个当最后一个工件在维护机器上加工时的算法,具体如下: 算法2 步骤1 根据不等式(1)、(5)、(6)以及k,k1,k2的唯一性计算k,k1,k2,如果k,k1,k2都存在,则继续步骤2,否则终止。 步骤2 验证不等式(3)、(4),如果不等式(3)、(4)都成立则继续步骤3,否则终止。 定理3 对于给定的工件和机器数量,如果满足不等式(5)、(6)的k1,k2存在,且不等式(3)、式(4)也成立,则由算法2得到的时间表长为最优时间表长且Cmax=k(T+w)+k1p。 证明 由不等式(3)~(6)的推导可知定理成立。 对于类型Ⅰ中最后一个工件在非维护机器上加工时有下面的不等式 化简有 (7) 除此之外,另外对于类型Ⅰ中最后一个工件在非维护机器上加工时还应满足 0 综合以上推断可得到下面的不等式 化简上述不等式(8),最后得到关于k2的不等式为 (9) 如果这样的k2存在,则k2是唯一的,由于工件在加工过程中不可中断,则k2只能取正整数,而且由不等式(9)知k2是唯一的。 对于k1则由不等式(8)可以得到 k2p-p-k(T+w) 化简有 (10) 由不等式(10)知k1也是存在唯一的。 归纳上述,最终得到一个当最后一个工件在非维护机器上加工时的算法,具体如下: 算法3 步骤1 根据不等式(1)、(9)、(10)以及k,k1,k2的唯一性计算k,k1,k2,如果k,k1,k2存在,则继续步骤2,否则终止。 步骤2 验证不等式(7)、(8),如果不等式(7)、(8)都成立则继续步骤3,否则终止。 定理4 对于给定的工件和机器数量,如果存在满足不等式(9)、(10)的k1,k2,且不等式(7)、(8)也成立,则由算法3得到的时间表长为最优时间表长,且Cmax=k2p。 证明 由不等式(7)~(10)的推导过程知定理成立。 算法4 步骤2 把n个任务按任意顺序排成一列,将这一列分为m部分,其中第i(1≤i≤n-zm)部分为[(i-1)(z+1)p,i(z+1)p],第i(n-zm+1≤i≤m)部分为[(i-1)zp+(n-zm)p,izp+(n-zm)p],转入步骤4。 步骤3 把n个任务按任意顺序排成一列,将这一列分为m部分,即第i(1≤i≤m)部分为[(i-1)zp,izp],转入步骤4。 文章主要研究了加工时长相等,且在加工过程中不可中断的n个工件被放在m台平行机上加工的调度问题,其中m台机器中部分机器需要周期维护,目标函数为最小化时间表长的平行机调度问题Pm,Pm1PM|pj=p|Cmax。本文根据周期维护的机器数量不同,提出了相应的求解的4个算法,并证明了通过相应的算法得到的时间表长为最优时间表长。后续将对工件具有不同加工时间的周期维护问题作进一步思考。



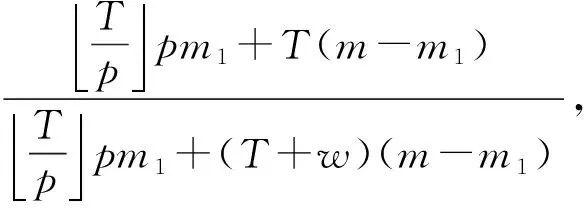











2.3 设m台机器中全部机器需要进行周期维护




3 结 语
