带有安装时间与维修活动的单机排序问题
2018-12-26赵玉芳葛秋利
赵玉芳, 葛秋利
(沈阳师范大学 数学与系统科学学院, 沈阳 110034)
0 引 言
生活中,带有维修和交货期窗口的问题受到了广泛的关注,具有重要的实际意义[1]。在某些情况下,在工件加工之前需要有安装时间,在加工过程中通过维修活动可以使机器的生产效率提高。Mor和Mosheiov[1]研究了带有交货期窗口和维修的单机排序问题;Wang等[2]研究了带有学习效应、退化效应和交货期窗口的单机排序问题;Cheng等[3]研究了维修时间与开始时间相关的带有退化效应和交货期窗口的单机排序问题;Janiak等[4]总结了关于交货期窗口的研究进展;王吉波等[5]讨论了同时具有学习和恶化效应的不同工期指派问题,并给出了多项式算法。
在带有安装时间的模型中,Koulamas和Kyparisis[6]提出了线性和非线性的安装时间模型,讨论了目标函数分别为最大完工时间、总完工时间及总完工时间的绝对差之和的单机排序问题,给出了计算复杂性都为O(nlogn)的多项式最优算法;Kuo和Yang[7]研究了带有安装时间和学习效应的单机排序问题;Wang等[8]研究了带有安装时间和学习效应与退化效应的单机排序问题;Huang等[9]讨论了带有安装时间、与位置有关的学习效应和退化效应的单机排序问题;Lee[10]讨论了带有安装时间与学习效应和退化效应的单机排序问题;关于带有交货期窗口和维修的问题,Mosheiov和Oron[11]研究了带有交货期窗口的单机排序问题,给出了计算复杂性为O(nlogn)多项式算法,对于加工时间与位置相关的带有交货期窗口的单机排序问题,给出了计算复杂性为O(n3)多项式算法;Wu和Ji[12]对于加工时间分别具有退化效应与学习效应的含有交货期窗口的单机排序问题进行了研究,给出了计算复杂性为O(n4)的多项式算法。
Zhao和Tang[13]研究了带有安装时间和交货期窗口与退化效应的单机排序问题,给出了计算复杂性都为O(nlogn)的多项式算法;Zhu等[14]研究了带有交货期窗口和维修的单机排序问题,其中维修存在资源且分为与位置相关和维修开始时间相关2种情况,给出了复杂性为O(n4)的多项式算法。在实际问题中,常常同时带有安装时间和交货期窗口与维修活动,本文同时考虑了带有上述情况的模型,并给出了在2种维修情况下的多项式最优算法。
1 问题描述
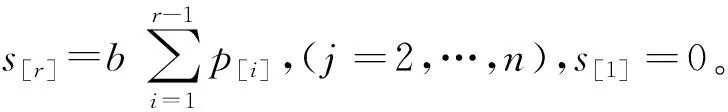
1=φ(0)≤φ(1)≤φ(2) ≤…≤φ(n-1)

用三参数表示法将2个问题分别表示如下:


其中tdcrm表示与时间相关的维修活动,pdcrm表示与位置相关的维修活动,Spsd表示安装时间。
2 对于带有固定长度维修活动的最优排序的性质
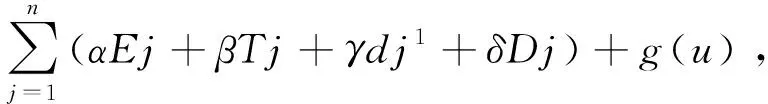



对于带有交货期窗口的单机排序问题,Mosheiov和Oron[10]证明了交货期窗口的开始时间和完工时间不能发生在工件加工过程中,且维修活动如果发生,必排在一个延误的工件之前。对于带有安装时间、维修活动和交货期窗口的单机排序问题也有同样结论。也就是:如果执行了维修活动,维修活动的开始时间一定被排在一个工件的完工时刻之后(或者在0时刻)。假设维修活动发生在第m个位置(l≤m),容易验证本文有类似的结论如下:
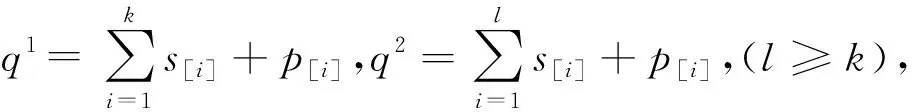
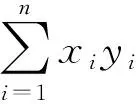
3 维修活动长度与时间相关的问题
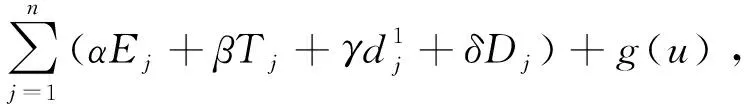
引理1 在最优排序中,若维修活动排在第m个位置,维修活动的位置只能属于下列3种情况之一:
情况1 维修并未发生,即m=n+1;
情况2 维修活动在开始处发生,即m=0;
情况3 维修活动排在交货期窗口之后,即l≤m 证明 假设排序为π=(J[1],…,J[n]),下面具体讨论这个问题: 1) 维修并未发生。 (3) 交货期窗口开始时间之和为 (4) 交货期窗口的长度之和为 因为未发生维修活动,所以g(u)=g(0)=0。 则目标函数为 其中Wj为j位置的权,有 为了得到目标函数Z的最小值,将工件的加工时间p[j]与j位置的权Wj按照相反的顺序排列。因此可以在O(nlogn)时间内得到最优排序。 2) 维修在机器开始加工时发生。 此时s=0,则维修活动的时间t(s,u)=t0+σs-τ(u)=t0-τ(u) (1)Ej=max(0,dj[1]-Cj),总提前量为 (3) 交货期窗口开始时间之和为 (4) 交货期窗口的长度之和为 则目标函数为 其中G(u)=γn(t0-τ(u))+g(u),Wj为j位置的权, 3) 维修在第m个位置发生,(l≤m (3) 交货期窗口开始时间之和为 (4) 交货期窗口的长度之和为 则目标函数为 其中G(u)=β(n-m)(t0-τ(u))+g(u),Wj为j位置的权。 家长要为孩子营造温馨、宽松、自由的阅读氛围。阅读时要安静,没有打扰,家长要带领孩子开展形式新颖、内容丰富的阅读活动。阅读时,家长要给予孩子想象的空间,鼓励孩子说出自己的想法,使孩子在愉悦的环境中快乐阅读。 假设j工件排在第i个位置上,那么xij=1,否则xij=0。为了得到目标函数Z的最小值,可以将其转化为指派问题: 其中: 对于资源分配的费用G(u)的最小值可以由u*=argmin{β(n-m)(t0-τ(u))+g(u)}得到,因为维修活动位置的不同,每一个位置需要求解一个相应的指派问题,因此可以在O(n4)时间内得到最优排序。 由以上讨论,得到定理1。 问题4与问题3的性质类似,下面分别在3种情况下分析: 情况1 维修并未发生,即m=n+1; 情况2 维修活动在开始处发生,即m=0; 情况3 维修活动排在交货期窗口之后,即l≤m 证明 假设排序为π=(J[1],…J[n]),维修活动的时间为t(m,u)=t0φ(m) -τ(u)。 维修并未发生与维修在开始时间发生的情况,与问题(1)和(2)一致,不再继续讨论,接下来讨论维修并未发生与维修在开始时间发生的情况,与问题(1)和(2)一致,不再继续讨论,接下来讨论维修在第m个位置发生的情况: 维修在第m个位置发生,(l≤m 3) 交货期窗口开始时间之和为 4) 交货期窗口的长度之和为 则目标函数为: 其中G(u)=β(n-m)(t0φ(m)-τ(u))+g(u),Wj为j位置的权, 假设j工件排在第i个位置上,那么xij=1,否则xij=0。为了得到目标函数Z的最小值,可以将其转化为指派问题: 其中: 对于资源分配的费用G(u)的最小值可以由u*=argmin{β(n-m)(t0φ(m)-τ(u))+g(u)}得到。因为维修活动位置的不同,每一个位置需要解一个相应的指派问题,因此可以在O(n4)时间内得到最优排序。 由以上讨论,可以得到下列定理: 本文研究了每个工件都有自己的交货期窗口、安装时间是加工时间的线性函数、维修带有资源的单机排序问题。其中维修活动使工件的加工时间缩短,可以通过资源分配使维修活动长度减少。目标是找到交货期窗口的大小和位置、维修的位置,使得提前惩罚、延误惩罚、交货期窗口的位置和长度、以及资源的总费用最小。在2种维修情况下,根据维修活动的位置不同分为3类,证明了问题是多项式可解的。另外,还可以在此基础上继续将模型推广,比如带有学习效应与退化效应的情况,也可以考虑工件的加工时间是带有资源分配的。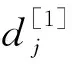

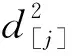

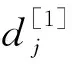

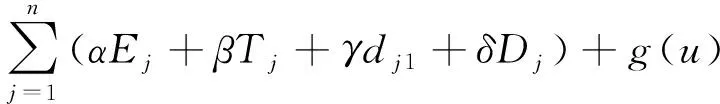
4 维修活动长度与位置相关的问题

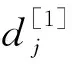

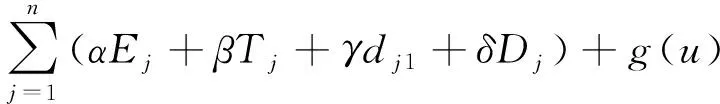
5 结 论
