上肢康复机器人动力学模型参数辨识

， ， ，

(南京工业大学机械与动力工程学院，江苏 南京 211816)

0 引言

传统的康复训练是由康复理疗师辅助患者进行肢体训练，整个康复过程需要进行大量、重复的康复运动，理疗师的劳动强度高并且无法满足国内众多偏瘫患者的训练要求。在这种情况下，使用机器人辅助理疗师对偏瘫患者进行肢体训练受到了广泛的关注，越来越多的康复机器人运用到康复治疗领域。由于康复机器人是一种非线性系统，很难建立精确的动力学模型，导致其运动控制精度不足[1-2]。因此建立精确的机器人动力学模型是提高机器人运动精度的关键因素。在机器人理论动力学模型的基础上，对动力学的参数进行系统辨识，可以得到更加精确的动力学模型[3-4]。

在此，设计了一款两自由度上肢康复机器人，使用拉格朗日法建立了该上肢康复机器人的动力学模型。针对该机器人特点，提出了用待定系数法将动力学模型转化为线性系统，得到了上肢康复机器人的动力学线性表达式。在ADAMS中使用PID控制算法控制其做圆周轨迹运动，将仿真中得到的转矩、关节转角、角速度和角加速度代入康复机器人的动力学线性表达式中，使用递归最小二乘法辨识动力学模型参数，得到精度更好的上肢康复机器人动力学模型。

1 上肢康复机器人运动学分析

上肢康复机器人采用双连杆机构，可以辅助患者进行平面运动。上肢康复机器人整体机构如图1所示。本文采用D-H表示法表述康复机器人的连杆坐标系，两自由度上肢康复机器人坐标简图如图2所示。

图1 上肢康复机器人三维模型

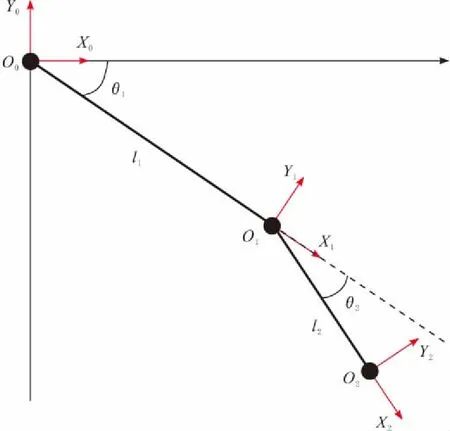
图2 两自由度康复机器人坐标简图

根据D-H表示法，连杆的齐次变换矩阵(D-H矩阵)通式为：

(1)

其中，C表示cos，S表示sin。

通过初等旋转变换和平移变换,将机器人的基坐标系变换为外框坐标系，得到的上肢康复机器人运动学关系式为：

(2)

其中，C12=cos(θ1+θ2)，S12=sin(θ1+θ2)。

2 上肢康复机器人动力学分析

上肢康复机器人动力学模型的标准形式为：

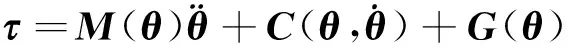
(3)

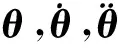
采用拉格朗日法计算两自由度上肢康复机器人动力学，得到如下方程：

(4)

为了简化参数辨识过程，可以将关节力矩进行线性化。将式(3)变换为惯性参数的线性形式：

(5)

3 动力学参数辨识方案

机器人动力学参数辨识一般包含激励轨迹设计、数据采样与处理、参数估计和模型验证4个步骤。上肢康复机器人动力学参数辨识过程可以描述为：给定康复机器人末端运动激励轨迹，采集康复机器人关节角度和关节力矩信息，数据经过处理后代入惯性参数表达式，求解康复机器人系统的惯性参数。整个操作的流程如图3所示[5]。

图3 机器人动力学参数辨识流程

3.1 参数估计方法

上肢康复机器人在PID控制策略下按照跟踪激励轨迹运动，运动过程中设计N个时间点对关节角度和电机力矩进行采样，获得N个采样点的数据。可以得到超静定线性方程：

(6)

式(6)是一个超静定线性方程，为了辨识得到两自由度上肢康复机器人动力学参数，文中采用递归最小二乘法求解该方程。惯性参数X的递归最小二乘法估计为：

(7)

根据最小二乘原理，康复机器人系统的最小二乘参数估计递推公式为[6]：

(8)

3.2 模型验证

为了验证辨识得到的动力学惯性参数的准确性，需要重新选取一条不同于激励轨迹的验证轨迹。将辨识得到的动力学模型预测关节力矩与实际输出的关节力矩进行对比，观察动力学模型是否可靠。实验验证过程如图4所示[7]。

图4 实验验证流程

4 辨识实验仿真

在ADAMS中建立上肢康复机器人的仿真模型，结合Simulink使该机器人在PID控制器下进行末端圆周运动，圆周轨迹的轨迹方程为：

(9)

4.1 参数估计

在该激励轨迹下，仿真实验的采样频率为200 Hz，在10 s的圆周运动过程中获得了2 004组关节输出转矩和关节位置的原始数据。

通过递归最小二乘法对获得的数据进行系统辨识，得到康复机器人的惯性参数。将得到的惯性参数代入康复机器人动力学公式中，求出机器人的预测力矩，该预测力矩与实际输出力矩如图5所示。将理想情况下理论计算的惯性参数代入康复机器人动力学公式，得到机器人的理论预测力矩，理论计算情况下的预测力矩与实际输出力矩如图6所示。

图5 激励轨迹下关节输出力矩和预测力矩比较

图6 理论计算的预测力矩和实际输出力矩比较

通过对比图5和图6可以看出，辨识后的预测力矩明显优于理想情况下的理论计算力矩，说明了采用递归最小二乘法进行动力学系统辨识的有效性。

4.2 模型验证

为了验证递归最小二乘法辨识得到的动力学参数的有效性，重新设计了1组不同于激励轨迹的验证轨迹，该验证轨迹的圆周半径为激励轨迹圆周半径的一半。将根据验证轨迹运动所得到的预测力矩和实际输出力矩进行比较，结果如图7所示。结果显示两者的拟合程度较高，说明最小二乘法辨识得到的上肢康复机器人动力学模型是有效的。

图7 验证轨迹下实际输出力矩与预测力矩比较

5 结束语

针对上肢康复机器人动力学模型不够精确问题，采用了递归最小二乘法辨识机器人动力学惯性参数。文中设计了圆周半径为100 mm的激励轨迹，根据递归最小二乘法辨识结果得到新的机器人动力学模型，使用圆周半径为50 mm的验证轨迹验证模型的有效性。结果表明，辨识得到的机器人动力学模型是有效的，为上肢康复机器人动力学控制系统开发打下了基础。