基于优化的元胞蚁群算法的无人飞行器 动态路径规划方法

,

(贵州民族大学数据科学与信息工程学院,贵州 贵阳 550025)

0 引言

路径规划是无人飞行器(UAV)研究的重要方向，已经引起了诸多学者的兴趣[1-2]。路径规划是依靠环境感知程度并在某些约束条件下，找出从出发点到目标节点的最佳飞行路线。

概率路线图法是一种常见的路径规划方法，采取随机抽样的方法选取无人飞行器的下一步的移动目标，并通过反复的随机抽样完成无人飞行器到目标节点的路径规划。目前有关概率路线图方法的研究已有许多文献，文献[1]针对未知环境中无人飞行器的路径规划问题，提出了一种适用于静态环境的路径规划方案，有效地改进了无人飞行器模拟路线的尖角问题和折返运动问题。文献[2-3]解决了传统概率路线图法在窄通道环境方面的不足，引入了人工势场方法，缩短了无人飞行器路径规划的时间。

蚁群算法是概率路线图方法的延伸。近些年来有关蚁群算法的无人飞行器的路径规划问题也引起了学者的注意。文献[4]为了克服路径搜索的盲目性，在蚁群算法的基础上引入了人工势场方法，将人工势场加入单蚁的信息素，有效降低了路径规划初期反馈不明显的影响。文献[5-6]用障碍物权重替代灰度矩阵，并引入一种新的启发因子影响路径抽样概率，既提高了无人飞行器的避障能力，又缩短了无人飞行器路径规划时间。

因此，在无人飞行器蚁群算法的基础上，提出了一种新的方案，每次采用多架次无人飞行器进行模拟，使用最优飞行路径进行信息素更新。同时，引入路径尖角优化策略对无人飞行器的飞行特征进行刻画。

1 传统PRM方法

传统的PRM算法依据飞行区域内的最小代价进行路径规划，并将其作为未知环境中路径移动的参考。遗憾的是，传统的PRM算法是借助随机抽样的原理，所规划出的路径并不一定符合无人飞行器的飞行特征。考虑图1中的无人飞行器路径规划问题，其中各节点的坐标如表1所示。进一步将地图离散化，节点之间可行区域用1表示，不可行区域用0表示，形成的矩阵被称为环境地图的灰度矩阵，如图2的映射被称为灰度映射。

图1 无人飞行器移动的环境地图

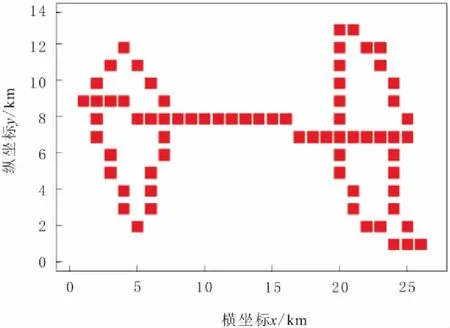
图2 环境地图的灰度映射

根据传统的PRM算法进行100架次的无人飞行器飞行模拟，模拟的最佳轨迹如图3所示。可以看出100架次无人飞行器的最佳模拟轨迹不仅存在折返跑的现象，而且其移动轨迹存在尖角，这些都不符合无人飞行器的飞行特征。

图3 基于传统PRM算法的无人飞行器移动轨迹

在实际飞行过程中，既不希望无人飞行器出现折返跑的现象，同时也不希望无人飞行器进行过大角度的转弯。基于此，利用无人飞行器的局部动态感知能力，对无人飞行器进行动态重规划，提出了一种基于元胞蚁群算法的局部动态PRM方法。

2 基于元胞蚁群算法和尖点优化的局部动态PRM方法

元胞蚁群算法是一种适用于并行计算的离散型算法。相比传统PRM算法，元胞蚁群算法不采用等概率进行路径选择，取而代之的是依据节点上的信息素浓度来确定抽样概率。

但是元胞蚁群算法在模拟初期容易出现搜索的盲目性和“蚂蚁迷失”现象。为此，本文全局上采用元胞蚁群算法和圈形轨迹优化相结合的方法进行路径规划，局部上采用尖点优化算法模拟无人飞行器的飞行特征，计算过程分为以下几个方面。

2.1 元胞蚁群算法构建

首先，对环境进行离散化建模，将地理环境进行网格化，依据无人飞行器的飞行特征(主要考察巡航高度)，确定出无人飞行器的可行飞行路线和可行区域，真实地理环境下的路线见图1，网格化以后的结果被称为灰度矩阵，矩阵上的每一点都和环境地图一一对应，可行用1表示，不可行用0表示，结果见图2。

其次，建立单蚁的元胞模型，其模型(用Model表示)简述为：

Model=(S,L,N,F)

(1)

S为元胞状态，Sn(i,j)=1表示经过n次移动单蚁处于节点(i,j)；L表示单蚁所有可能到达的位置节点即元胞空间；N为元胞邻居，通常用N(Sn)表示，它表示结合无人飞行器的飞行特征，筛选出的无人飞行器n+1次移动后可能到达的位置节点，如图4所示。N(Sn)={si|i=1,2,…,8}，i为方向序号，s3=1则表示在进行n+1移动时，单蚁选择3号方向，反之，若s3=0，则表示不选3号方向。

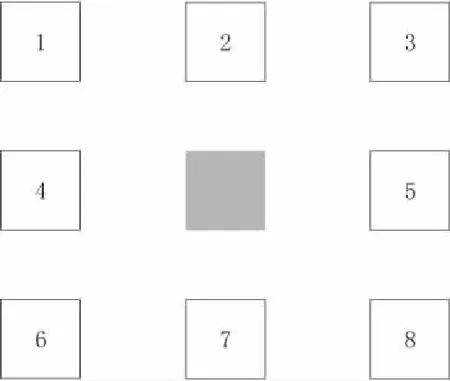
图4 Moore元胞邻居模型

为了方便论述，用Φ(n)表示经过n次移动后无人飞行器所处的位置(i,j)，通常记为Φ(n)=(i,j)。元胞蚁群算法就是确定一个转换函数F，依据转换函数F并结合尖角优化策略，在元胞邻居中选择下一个坐标Φ(n+1)，即

Φ(n+1)=F(Φ(n))

(2)

最后，利用优化后的最优路径进行无人飞行器的信息素更新，这样可以最大限度地使得蚁群算法在最优路径上富集更多的信息素。若无人飞行器在优化后的轨迹上按照概率pk选择了元胞邻居N0(Sn+1)的第k个节点，那么第k个节点的信息素采用的局部更新规则为：

τk←(1-r)τk+rΔτk

(3)

这里r为常数，表示信息的挥发系数。假定元胞邻居N0(Sn+1)的第k个节点为Φ(n+1)，则有：

(4)

d(Φ(n),Φ(n+1))为节点Φ(n)和节点Φ(n+1)之间的距离。

2.2 尖点优化以及圈型轨迹的消除

在式(2)中，引入尖点优化最大限度地消除蚁群算法引起的无人飞行器折返跑现象。在尖点优化规则下，确定状态转移规则F和信息素更新规则。假定已经经历n次转移处于节点Φ(n)，并假定下次转移处于节点Φ(n+1)，并假定Φ(n-1)、Φ(n)和Φ(n+1)之间的夹角为Angle(n)。则尖点优化规则如下所述。

a.对Moore元胞邻居中的任意节点Φ(n+1)∈N(Sn)，若

Angle(n)>100°

(5)

则认为Φ(n+1)∈N0(Sn)。

b.若不存在任何节点Φ(n+1)∈N(Sn)使得Angle(n)>100°，则认为：

N0(Sn)=N(Sn)

(6)

利用元胞蚁群算法，将在新的元胞邻居N0(Sn+1)中进行随机抽样作为下一次移动的目标节点，抽样的概率为：

(7)

τk为元胞邻居N0(Sn+1)中第k个节点的信息素。

接下来进行单轮无人飞行器模拟的最优路径的选择。选择的结果将用于信息素的更新。除路径最短方案之外,本文做了另一方面的改进：在更新之前进行圈形轨迹的识别和剔除，保证以后的飞行模拟最大限度地避免无人飞行器折返跑问题。在圈形轨迹的识别方法中，假定根据最短路径确定出来的移动路径为：

S0,S1,…,Si,Si+1,…,Sj,Sj+1,…,Sn

(8)

S0为起点,Sn为目标点。若检测发现Si=Sj,则将路径优化为：

S0,S1,…,Si,Sj+1,…,Sn

(9)

当确保最优路径没有重复节点之后,说明优化后的最优路径已不存在圈型轨迹。

2.3 实验算法设计

在不引起混淆的前提下，将圈形轨迹优化和尖点优化统称为路径优化。将路径优化策略融入元胞蚁群算法，那么基于路径优化的蚁群系统算法步骤如下：

a.建立灰度矩阵H，将地图离散化。

b.设置飞行模拟次数n和每次模拟的无人飞行器数量m。

c.设置信息素矩阵IM，维数和灰度矩阵H相同，所有元素取值为1。

d.飞行次数的循环开始for(i= 1:n)。

e.飞行器数量的循环开始for(j= 1:m)。

f.while循环(或者repeat)开始，直至寻找到目标节点停止。

g.假定第i次循环的第j个无人飞行器所处的位置为Poisition(i,j)，依据灰度矩阵确定其元胞邻居中的可行区域。

h.进行尖点优化，将可行区域内不符合飞行角度的节点剔除。

i.按照信息素确定的抽样概率，在可行区域内进行随机抽样确定下一节点。

j.while循环结束。

k.飞行器数量的循环结束，确定了m条路径，按照距离最短选择本次模拟的最优路径。

l.对最优路径进行圈形轨迹的识别，剔除圈形轨迹。

m.按照优化后的最优轨迹进行信息素更新，选择Q=m，r=0.05。

n.飞行次数的循环结束，综合n次飞行模拟的结果选取最优的路径。

在设计好实验算法之后，将尖点优化的蚁群系统算法进行数值模拟，与此同时也将尖点优化方案用于常规的PRM算法，并将2种方案所得结果进行比对。

3 仿真验证

为了验证本文所提出方法的正确性和有效性，采用30架无人飞行器进行运算(运算10次的结果如图5所示，运算20次的结果如图6所示)。在和图3相同的环境下，设置初始位置为(2,8)、目标节点为(24,11)，采用尖角优化的蚁群系统算法进行规划，并选取30架无人飞行器的最优路径进行信息素的更新，每次更新的信息浓度为30，模拟结果如图5和图6所示。

对比图6和图3可以看出，基于尖角优化的蚁群系统算法经过了最少的节点，路径距离也是最短。值得读者注意的是图5规划的路径没有直接经过节点F和节点G，这是因为在灰度映射中网格剖分不够细致所致，见图2。再对比图5和图6还可以看出随着运算次数的增多，结果更加精确。

图5 基于尖角优化的蚁群系统算法(运算10次)

图6 基于尖角优化的蚁群系统算法(运算20次)

4 结束语

引入尖点优化策略和圈型轨迹检索算法之后，模拟结果更加符合无人飞行器的动力特征,也有利于操控的稳定性。对比传统元胞蚁群算法，进行尖角优化策略和圈型轨迹算法优化之后，无人飞行器的最优路径更加平滑。