尖点突变理论在边坡抗震稳定分析中的应用
2020-09-25于勉
于 勉
(高邮市水利建筑安装工程总公司,江苏 高邮 225600 )
当使用强度折减法[1- 3]进行边坡动力稳定分析时,结果的准确性与所用失稳判据关系密切。塑性区贯通、迭代不收敛和关键点位移突变判据是目前常用的动力失稳判据。其中,塑性区贯通无明确客观指标;迭代不收敛在动力工况下的不收敛判定标准尚不明确和统一;关键点位移突变判据对突变点位置的判定受主观因素影响较大。为了使关键点位移突变判据结果更为客观,部分学者利用尖点突变理论来判定位移突变位置,如宋鑫华、包太等[4]运用尖点突变理论研究土质边坡的稳定性;史俊涛、孔思丽等[5]将尖点突变模型运用到非均质土坡稳定分析中,结果表明:尖点突变模型求解出的安全系数精度较高;戴妙林、李强伟等[6]将尖点突变理论分别应用于均质土坡和岩质边坡,结果表明:尖点突变模型计算出的安全系数与极限平衡法计算出的结果相近,其在均质土坡和岩质边坡中的应用是可行的。但目前尖点突变理论在边坡抗震稳定分析中的应用较少,文章将尖点突变理论应用于边坡动力分析中,通过建立坡顶关键点水平向震后残余位移与强度折减系数的尖点突变模型,进而定量给出边坡的动力安全系数,并将计算结果与塑性区贯通判据结果进行对比,以此说明尖点突变理论在边坡抗震稳定分析中的应用是可行的。
1 计算理论与方法
1.1 强度折减法
强度折减法固定地震荷载不变,把边坡现状抗剪强度参数(c,φ)等比例折减k倍,然后用折减之后的边坡抗剪强度参数(c1,φ1)进行动力时程分析,计算公式如下:
(1)
定义使边坡达到临界动力失稳状态时对边坡抗剪强度参数(c,φ)的折减程度k为动力安全系数。
1.2 失稳突变模型
为避免人为判断震后残余位移突变点位置产生误差,通过构造尖点突变模型[7]用数学判别式来定量搜寻突变点的位置。假设震后残余位移E是随边坡动力折减系数k变化的连续函数,并进行四次泰勒级数展开,则
E=f(k)=a4k4+a3k3+a2k2+a1k+a0
(2)

E=b4c4+b2c2+b1c+b0
(3)
式中,

(4)
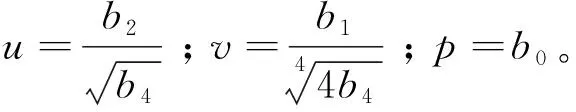
对式(4)求导,令导数等于0,即得平衡曲面方程
x3+ux+v=0
(5)
其分差集方程为
4u3+27v2=0
(6)
令
Δ=4u3+27v2
(7)
当Δ>0时,系统处于稳定状态;当Δ=0时,系统处于临界状态;当Δ<0时,系统失稳破坏。
2 算例分析
2.1 计算模型
边坡尺寸及有限元模型分别如图1、图2所示,强度准则选取Mohr-Coulomb准则,具体材料参数见表1。

图1 边坡模型尺寸

图2 有限元计算模型

表1 边坡材料物理力学参数表
文章基于规范反应谱[8]以阻尼比5%,动力放大系数βmax=2.5合成一组水平向峰值加速度为0.2g和竖向峰值加速度为0.133g人造地震波。人造波持时20s,计算步数为2000,步长0.01s,如图3所示。

图3 地震加速度时程曲线
文章采用黏弹性边界[9]来模拟远域地基辐射阻尼对地震波的影响,并将地震波转换成等效节点力[10]施加在边界上。
2.2 位移突变判据
提取关键点A的水平向震后残余位移并分绘制其与动力折减系数的关系曲线(图4),从图4中可以看出关键点A位移突变的位置处于k=1.35~1.4之间,具体突变位置需根据尖点突变理论来判定。
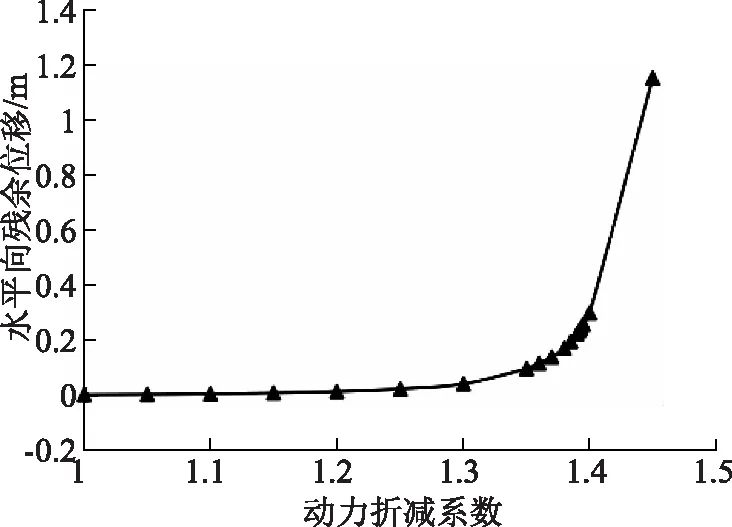
图4 关键点水平向残余位移与动力折减系数关系曲线
图5和图6分别为k=1.38和k=1.39时的关键点残余位移与动力折减系数的拟合曲线,可以看出两条拟合曲线的R2分别为0.9979和0.9946,都很接近1,说明拟合效果较好。

图5 k=1.38时关键点水平向残余位移与动力折减系数拟合曲线

图6 k=1.39时关键点水平向残余位移与动力折减系数拟合曲线
根据图5,当动力折减系数k=1.38时,根据式(2)~式(7)对前10个包括k=1.38共11个动力折减系数进行四次多项式拟合,得到下式:
E=54.385k4-248.1k3+423.66k2-
320.83k+90.895
(8)
简化后代入式(4)得突变模型标准式:
(9)
得到:Δ=4u3+27v2=4·(-0.10443)+27·0.03042=0.02。
根据图6,当动力折减系数k=1.39时,同上,对前12个包括k=1.39共13个动力折减系数进行四次多项式拟合,得到下式:
E=80.397k4-370.14k3+637.46k2-
486.62k+138.91
(10)
简化后代入式(4)得突变模型标准式:
(11)
得到:Δ=4u3+27v2=4·(-0.17553)+27·0.02352=-0.0067。
结果显示:当k=1.38时,Δ=0.02>0,此时边坡结构稳定;当k=1.39时,Δ=-0.0067<0,此时边坡失稳破坏。所以边坡动力安全系数处于1.38~1.39之间,为了安全考虑,动力安全系数定为1.38。
2.3 塑性区贯通判据
随着折减系数的增大,岩土材料在不断软化,塑性区从边坡最薄弱的地方慢慢开展直至贯通。如图7所示,当k=1时,塑性区只产生于坡脚一小块区域内,随着k的不断增大,塑性区慢慢向坡顶扩展;当k=1.32时,塑性区延伸到坡顶,边坡产生了贯通坡顶和坡脚的滑裂带。

图7 边坡塑性应变云图
由塑性区贯通判据计算出的边坡安全系数为1.32,小于位移突变判据给出的安全系数1.38,说明塑性区刚刚贯通时,边坡还具有一定的承载力,并未整体失稳,正好印证了塑性区贯通是边坡失稳的必要非充分条件这一观点[11]。
3 结论
(1)通过建立坡顶关键点水平向震后残余位移与折减系数的尖点突变模型,可以定量给出边坡的动力安全系数,所得结果稍大于塑性区贯通判据结果,证明了尖点突变模型在边坡动力稳定分析中的应用是可行的。
(2)由于边坡动力问题的复杂性,建议在确定边坡动力安全系数时综合运用位移突变判据和塑性区贯通判据。
