基于曲波变换的轮胎花纹特征提取及水印算法

刘 颖, 张 江, 燕皓阳, 张倩楠, 葛瑜祥, 朱婷鸽

(1.电子信息现场勘验应用技术公安部重点实验室, 陕西 西安 710121；2.西安邮电大学 图像与信息处理研究所，陕西 西安 710121； 3.陕西省公安厅 刑侦局技术处，陕西 西安 710018)

轮胎作为汽车特有部件，具有极好的辨识度和特异性，轮胎花纹的图像具有颜色单一，纹理复杂、曲线多和方向较为统一的特点。因此，基于纹理特征的轮胎花纹图像数据库查询是交通事故处理和刑侦破案中一项重要的工作，纹理特征提取的有效性决定了查询检索效率。

小波变换(discrete wavelet transform，DWT)[1-2]是一种常用的纹理特征多尺度分析方法，但这种方法不具有旋转不变形、解析方向少且对曲线不敏感[3]。脊波变换(ridgelet transform)是在小波变换的基础上提出的一种多方向的对尺度分析法，它在小波变换中加入了一个表征方向的参数，因此脊波变换具有更多的解析方向，但仅对直线纹理敏感。曲波变换利用积分思想把曲线近似为极小的直线段集合，对每段微小直线进行脊波变换，即可利用直线的方向特性来表示曲线[4]。虽然曲波变换(curvelet transform)[5-8]对曲线和复杂纹理具有良好的解析特性[9]，且解析方向也从小波变换的4个变为8个，但曲波变换仍不能克服旋转对检索效果的影响。

利用曲波变换的子带能量分布特性，结合轮胎的纹理特征方向性，本文提出一种基于能量分布的纹理特征提取算法。根据刑侦图像的特殊安全性，需在图像中加入数字水印[10-13]，为了最大程度地降低嵌入水印对原始纹理信息的影响，本文在提出纹理特征提取算法的基础上又给出一种基于曲波域能量分布的数字水印嵌入算法。

1 基于曲波变换的纹理特征提取

1.1 轮胎图像的曲波变换

选取一副轮胎花纹图像进行离散曲波变换，定义f[t1,t2]，0≤t1≤t2≤n，离散Curvelet变换为

(1)

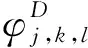
图1 轮胎花纹曲波变换与曲波变换频带划分

1.2 轮胎花纹的纹理方向和能量特征

通过对轮胎花纹图像曲波变换子带系数的分析，比较各子带系数的分布情况，可将轮胎花纹分为垂直导向型、水平导向型、对角导向型和不规则型，如图2所示。

分别对图2中4种不同方向类型的轮胎花纹进行2层曲波变换，再统计各子带能量所占整个高频子带能量的百分比，结果分别如表1和表2所示。

图2 轮胎花纹的分类

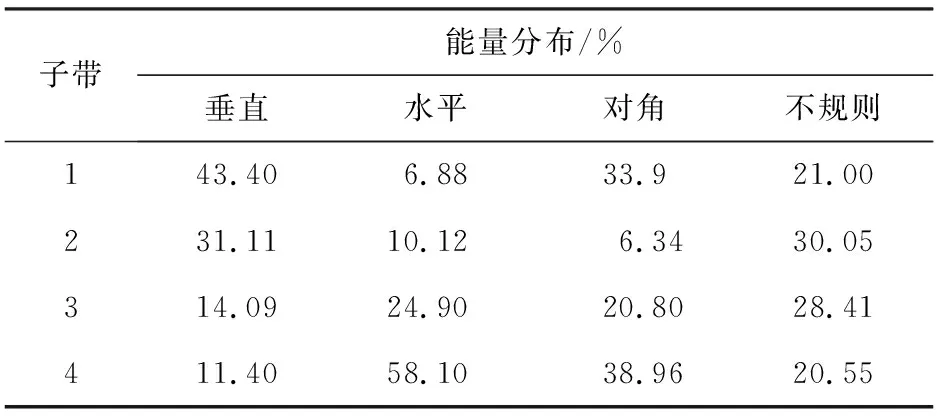
表1 第1层高频子带S2的能量分布

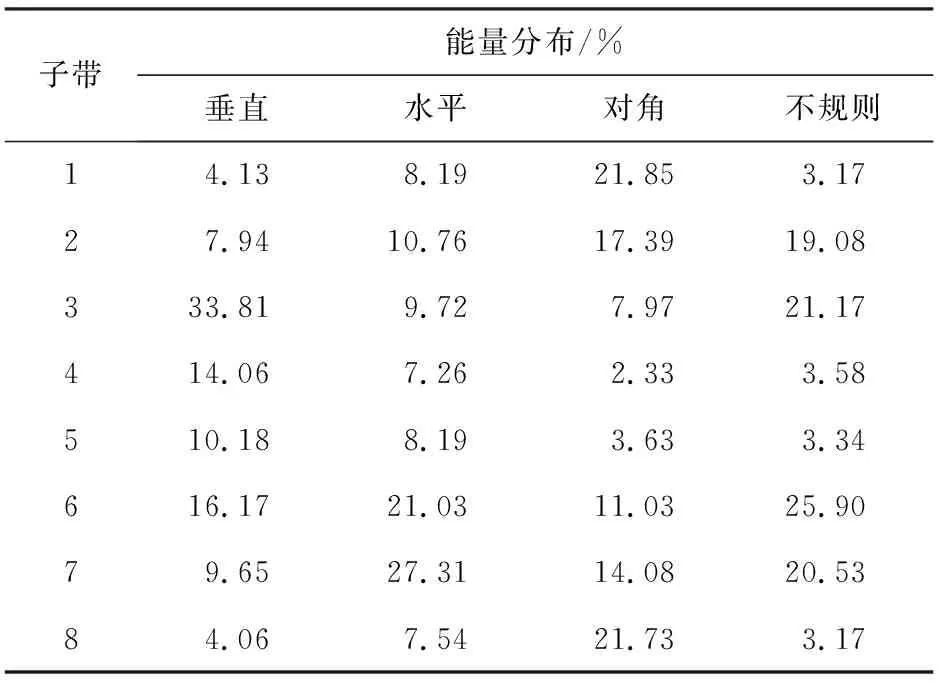
表2 第2层高频子带S3的能量分布

由表1和表2可以看出，垂直导向型的轮胎能量主要集中在S2的1、2子带和S3的2、3子带；水平导向型的轮胎能量主要集中在S2的3、4子带和S3的6、7子带；对角导向型的轮胎能量主要集中在S2的1、4子带和S3的1、8子带；不规则型的能量在各子带分配较为均等。

轮胎花纹各个方向的能量对应子带系数分配到相应方向的子带上，子带方向与轮胎花纹的主要纹理方向相同的子带所含能量最高，子带系数也最大[17]。

1.3 能量分布算法

曲波变换的能量分布和花纹方向关系非常密切，若轮胎花纹图像发生旋转，则曲波变换的系数也会随旋转而发生变化。将图2(a)的轮胎花纹顺时针旋转90°，即垂直导向型变为水平导向型的花纹图像，如图3所示。

图3 旋转后图像

分别对图2(a)和图3进行2层曲波变换，统计高频自带系数能量分布，结果如表3所示。

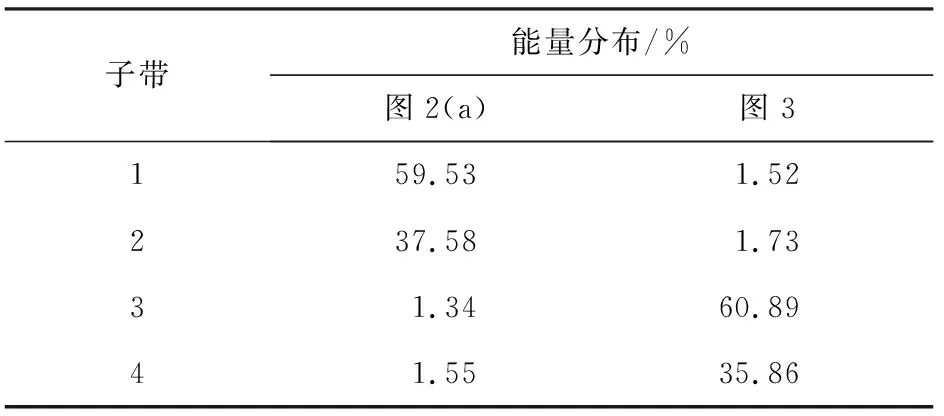
表3 旋转前后一层高频能量分布

由表3可知，旋转前后两图像的各子带系数数值变化不大，只是位置发生了变化，且这种变化正好对应了轮胎旋转后纹理导向的变化。由此,提出了具有旋转不变性的曲波能量分布算法。

为避免3层曲波变换带来的信息冗余和1层曲波变换解析方向少的问题，采用2层曲波变换。取2层曲波变换各子带系数的均值(M)和方差(σ)作为纹理特征，每幅轮胎花纹图像分解后的第1层高频部分的1～4子带，第2层高频部分的1～8子带，以及1个低频近似子带，共13个子带实部和虚部的均值和方差形成52维的特征向量。

(2)

(3)

特征向量可表示为

f=(M1,σ1,M2,σ2,…,M52,σ52)。

(4)

此时的纹理特征向量还不具有旋转不变性，需要对特征向量根据曲波变换能量分布进行排序和平移：分别计算13个子带的均值及方差，按第1层高频子带，第2层高频子带，低频近似子带的顺序排列成52维的原始特征向量；计算第1层和第2层高频部分各子带占本层总能量的百分比，并对高频能量分布进行排序，找出各层能量最高部分所在的子带，把能量最高部分所在的子带称为基准子带；对整个原始特征向量进行循环平移，直到基准子带被移动到特征向量的首部，即移动后每幅图像特征向量的前两个分量为基准子带的均值和方差。通过上述过程，无论图像经过怎样的旋转，其基准子带必然在特征向量的队首，并且各分量之间的排列关系不会被打乱，即保持了各特征向量的奇异性，这样就消除了旋转所带来的影响。算法流程如图4所示。

图4 算法流程

1.4 纹理特征提取算法实验结果

为了验证纹理特征提取算法是否能有效提取轮胎花纹的纹理特征及图像旋转所带来的查准率下降问题，通过Matlab2012b软件对含有200幅40组轮胎花纹图像的轮胎花纹数据库，分别进行小波变换算法、曲波变换算法和本文算法检索对比实验，实验以查准率P=N/k衡量检索性能，其中k表示检索结果前k幅图像，N为前k幅图像中与查询图像相似的图像数目。取k=6，实验结果如图5所示，多组查询的平均查准率曲线如图6所示。

由图6可见，小波变换算法的查准率为59.1%，曲波变换算法的查准率为68%，小波变换和曲波变换不具有旋转不变性，在图像发生旋转时其性能较差，而本文算法查准率达到79.5%，克服了因为图像旋转所带来的检索查准率下降问题。

2 基于曲波域能量分布的数字水印

2.1 水印嵌入

基于刑侦图像的特殊信息安全要求，通常需在图像中加入数字水印，而嵌入数字水印容易改变原始图像的信息。变换域数字水印对于图像纹理特征提取的影响主要在于[18]：当数字水印被嵌入与图像经过变换的变换域系数后，变换与系数发生了改变，图像的纹理特征值正是从这些变换域系数中计算得出，若变换域系数发生变化，图像的纹理特征值即会相应发生变化。

为了克服上述影响，给出一种与基于曲波能量分布的数字水印算法相结合的数字水印算法。

水印嵌入算法的主要步骤如下。

步骤1利用式(1)、式(2)和式(3)，对未嵌入水印的原始图像进行2层曲波变换，计算各层子带能量分布情况，标记第2层能量最大子带的编号。

步骤2将水印图像置乱后嵌入于能量最大的曲波子带。

采用Torus自同构映射对原始水印图像进行置乱，置乱公式为

(6)

其中(xi,yi)∈[0,n-1]×[0,N-1]，原始水印图像大小为N×N，k∈[0,N-1]为映射次数，W即为原始水印图像经过k次映射后的结果。

嵌入公式为

C′(i,j)(m,n)=C(i,j)(m,n)+αW(i,j),

(7)

其中C为被嵌入子带的系数，α为嵌入强度因子，α越大则嵌入水印信号越强，鲁棒性越好，但不可见性也随之降低，若α太小，则水印信号太弱，抵抗攻击能力较差。

步骤3对嵌入水印后的图像系数进行曲波逆变换，得到含有数字水印的水印载体图像。

由此，原本能量最大的子带会具有更大的能量，在提取特征值时，保证了能量最大子带部分仍具有较高能量，相对于其他算法，该水印嵌入算法可以较好地克服系数带来的变化，降低系数改变可能造成的能量分布变化，能够做到刑侦图像检索中安全性与检索效率的结合。

2.2 水印提取

载体图像经过信道传输或其它传输方式后，就需要从载体图像中提取水印。数字水印提取算法的主要步骤如下。

步骤1对载体图像进行与嵌入算法中原图像相同的曲波变换算法。

步骤2计算各子带能量分布，标记能量最大的子带编号。

步骤3对原始图像进行曲波变换，计算各子带能量分布，标记能量最大子带编号。

步骤4将载体图像能量最大子带的系数矩阵与原始图像能量最大子带的系数矩阵进行判决

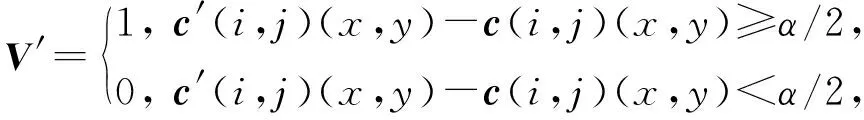
(8)

其中，c′为载体图像能量最大子带的系数矩阵，c为原始图像能量最大子带的系数矩阵，V′即经过判决后提取出的未经反置乱的数字水印。

步骤5在得到V′后，对V′进行反置乱，反置乱次数与嵌入算法中之乱次数k相同。

数字水印嵌入和提取算法的流程分别如图7和图8所示。

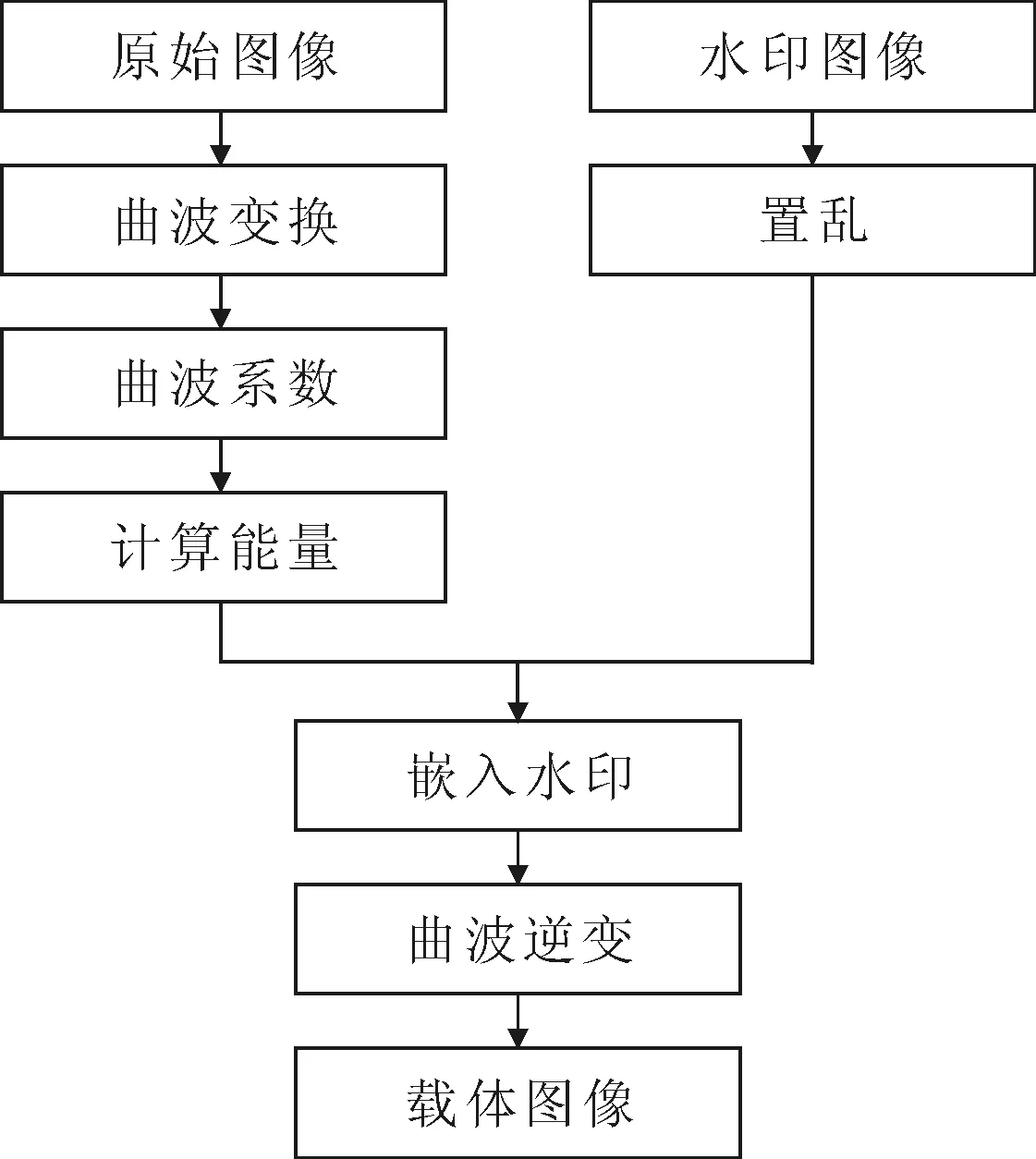
图7 数字水印嵌入算法流程

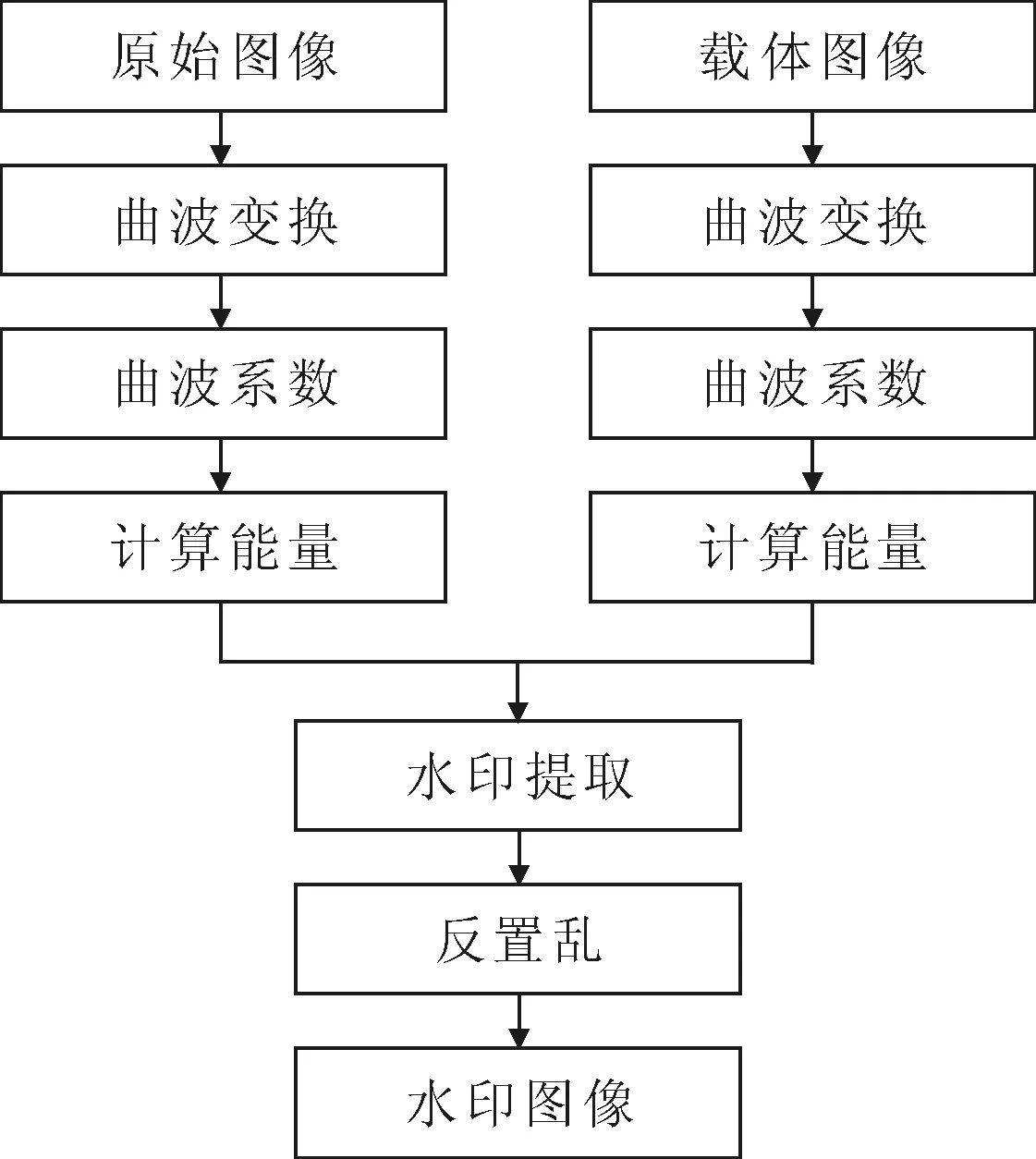
图8 数字水印提取算法流程

3 数字水印算法结果分析

为了从主观和客观两方面对基于曲波能量分布的数字水印算法进行评价，实验通过Matlab 2012b软件对50幅轮胎花纹图像测试本文算法的不可见性、鲁棒性和嵌入本水印后的检索效果[19-21]。选用1幅大小为128×128的含有“西安邮电大学”字样的灰度图像作为数字水印，水印图像及其置乱k=12次后的置乱图像如图9所示。

图9 数字水印及其之乱后图像

3.1 不可见性测试

将水印嵌入轮胎花纹图像，采用主观观察与计算峰值信噪比(PSNR)两种方法判断算法的不可见性。两组原始轮胎花纹图像及嵌入数字水印后的轮胎花纹图像如图10所示。

图10 原始图像及加水印后图像

由图10可以看出，轮胎1和轮胎2的原始图像与嵌入数字水印后的图像非常接近，该数字水印算法在主观上具有较好的不可见性。分别计算两幅图像的PSNR，轮胎1的PSNR结果为49.96，轮胎2的PSNR结果为50.53。当PSNR>30时，人眼就很难分辨出原始图像和加水印图像的差别，更加说明该数字水印算法具有较好的不可见性。

3.2 鲁棒性测试

以图10(a)轮胎1为例，对嵌入水印后的轮胎花纹图像分别进行攻击模拟[22-23]，攻击方式分别为椒盐噪声攻击(δ=0.1)，高斯噪声攻击(δ=0.08)，JPEG压缩，剪裁攻击和旋转攻击(顺时针5°)，鲁棒性测试结果如图11所示。

图11 5种攻击方式的鲁棒性测试结果

计算各攻击后提取水印结果的NC值，将计算结果与文献[24]方法进行对比，对比结果如表4所示。

由表4可以看出，本文算法的NC值在椒盐噪声攻击(δ=0.1)，高斯噪声攻击(δ=0.08)，JPEG压缩，剪裁攻击，旋转攻击(顺时针 )这5中不同的攻击方式下，均高于文献[24]的方法，即具有较好的鲁棒性。

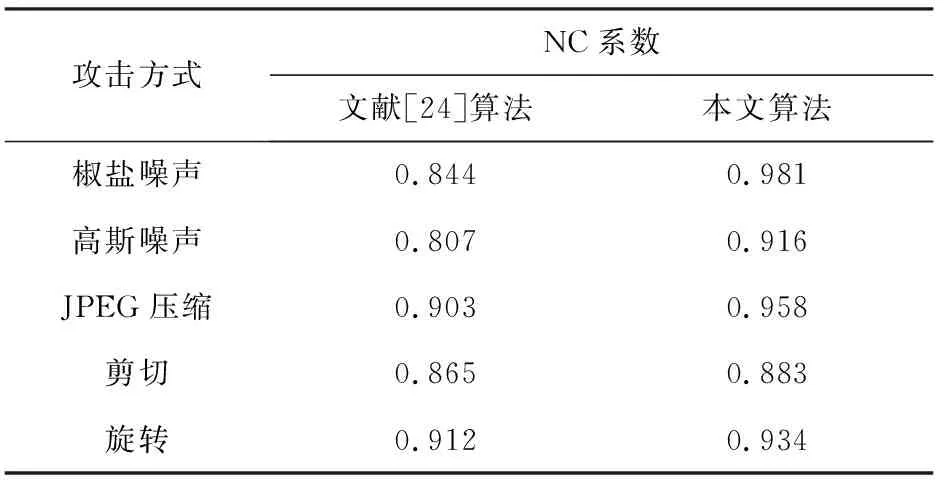
表4 水印算法鲁棒性实验结果

3.3 轮胎花纹检索测试

分别选取LSB算法和小波变换算法与本文算法对轮胎花纹数据库进行水印嵌入。用未嵌入数字水印的轮胎花纹图像在嵌入数字水印后的轮胎花纹数据库中进行纹理特征提取和检索实验，实验结果如图12所示。

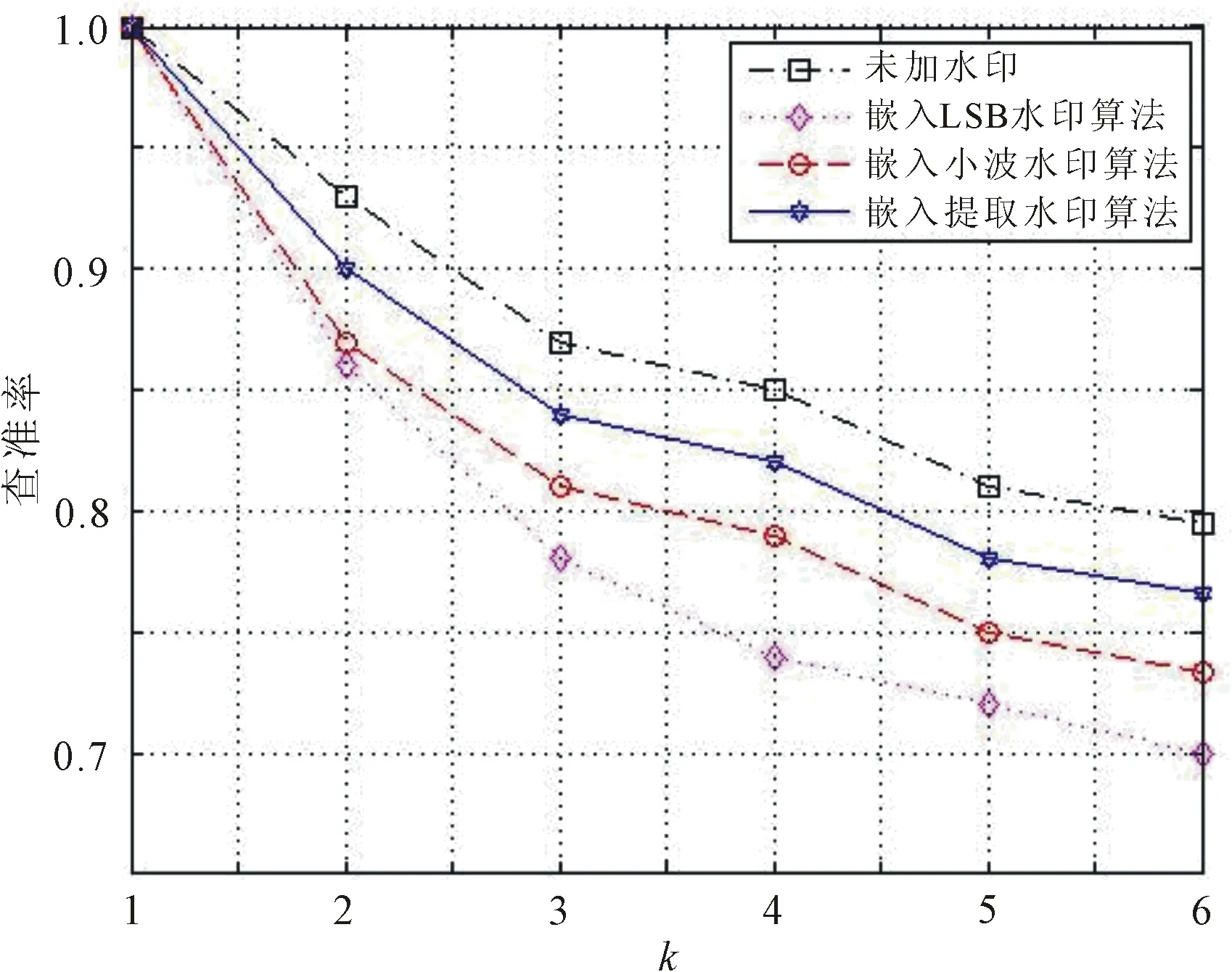
图12 嵌入水印检索实验结果

由图12可以看出，嵌入水印均对图像检索结果产生了影响，其中LSB算法的影响最大，当k=6时查准率为70%，查准率比不加水印时下降了9.5%，而使用小波变换水印嵌入算法时查准率为73.3%，其查准率比不加水印时下降了6.2%，使用本文算法的查准率为76.6%，比不加水印时下降了2.9%，即查准率影响较小。由此可以证明，所给数字水印嵌入算法具有较好的不可见性与鲁棒性，在经过各种攻击后仍能提取出较清晰的水印，且适应于基于曲波能量分布的纹理特征提取算法，对纹理特征的影响最小。

4 结语

基于曲波能量分布的纹理特征提取算法，利用曲波变换的子带能量分布特性，结合轮胎的纹理特征方向性，可有效提取轮胎花纹的纹理特征且具有良好的旋转不变性。与小波变换算法、曲波变换算法对比实验结果表明，该算法查准率可达79.5%，加入数字水印嵌入算法后的查准率为76.6%，具有较好的不可见性与鲁棒性，且对图像纹理特征的影响较小。