Feature selection in super-resolution onself-learning neighbor embedding
2018-12-26XUJianXINGJunFANJiulun
XU Jian,XING Jun,FAN Jiulun
(1. Key Laboratory of Electronic Information Application Technology for Scene Investigation,Ministry of Public Security, Xi’an 710121, China;2. International Joint Research Center for Wireless Communication and Information Processing, Xi’an 710121, China;3. School of Communication and Information Engineering, Xi’an University of Posts and Telecommunications, Xi’an 710121, China)
Abstract:Several feature extraction methods are proposed to extract patch features in low-resolution (LR) space, and their abilities in selecting high-resolution (HR) patches are tested. As neighbor embedding (NE) is highly related to the training sets, the self-learning method is employed to produce the training sets. It can be found that some LR features can obtain higher-quality HR patches which are very similar with the desired HR patches. Experimental results on self-learning show that the proposed methods provide different HR results, some of them have good effect and high efficiency. The obtained features can be used for NE based super resolution (SR) algorithm and can well remit one-to-many ill-posed problems.
Keywords:self-learning, feature extraction, super-resolution algorithm
Single image SR is an image processing technique that can convert a LR image into a HR image[1]. The learning-based SR algorithms are greatly developed in recent years[2-4]. These algorithms train machine learning models by a set of training samples containing HR-LR patch pairs[5]. In the training process, it is not popular to directly use pixel values, but features are always extracted from HR-LR patch pairs (such as gradient[6], midfrequency feature[7], et. al). From experimental results of these algorithms, we can observe that different image features lead to different outputs.
The requirement of feature extraction in single image SR is different from other image processing areas, such as image registration[8-10]. It needs to extract features in LR space and finds the candidates in HR space. Since LR patch has much less pixel numbers than its corresponding HR patch, the problem is under-determined. One LR image patch may correspond to many HR image patches (which is called one-to-many problem) , so the mis-selection is not avoidable. Different image features result in different mis-selection. Although most of the image features have no capability to find the real corresponding HR patches, some features can find HR patches that are similar with real corresponding HR patches.
We try to analyze the performance of different features in SR area. There are three factors that can effect the performance: (1) The topic of training set. The training set which belongs to the same topic with the test set will get a better HR result[11]. (2) The feature extraction methods which extract features from LR patches. (3) The model of machine learning. We only want to observe the effect of feature extraction. To avoid the effects of machine learning models, we find LR patches by using different features and then compare the corresponding HR patches with the desired HR patches. This process avoids choosing weights of overlapping patches and only assesses the quality of patch matching. To avoid an impact on the training sets, we use self-learning method to generate training sets[2,12-13].
Our contributions can be summarized as: (1) We propose several feature extraction methods which can be utilized as candidates in SR methods. (2) We test the features’ capabilities of selecting HR patches. These experimental results show different phenomena of one-to-many problems. (3) We utilize these features on the self-learning algorithm. Experimental results show that some features can improve effect and efficiency of self-learning algorithm.
The rest of this paper is organized as follows. Section 1 describes the process of building two pyramids and four data sets in detail. Section 2 presents different feature extraction methods. The experimental results are described in Section 3. Section 4 concludes this paper.
1 Data generation based on self-learning
1.1 Generating pyramids
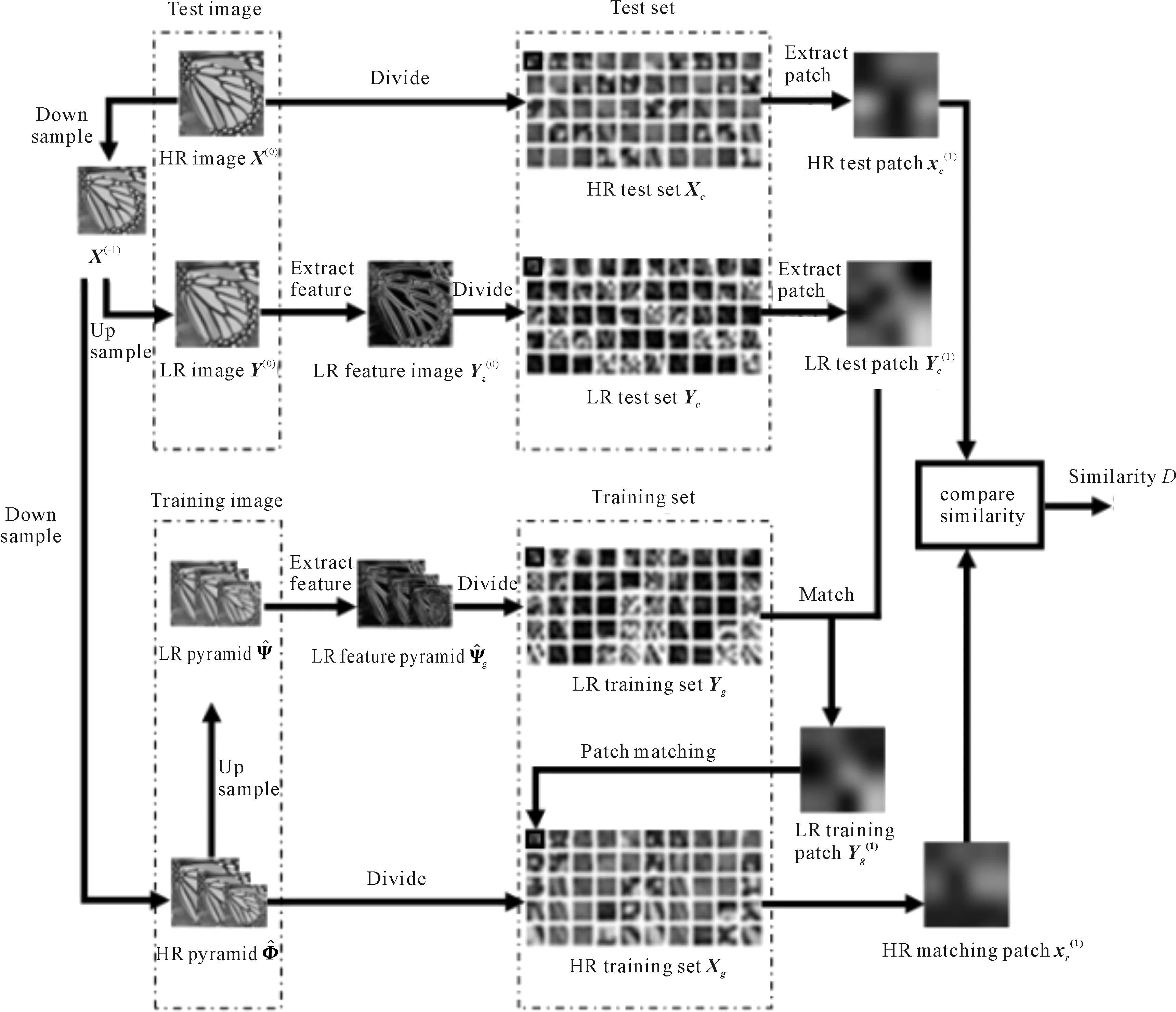
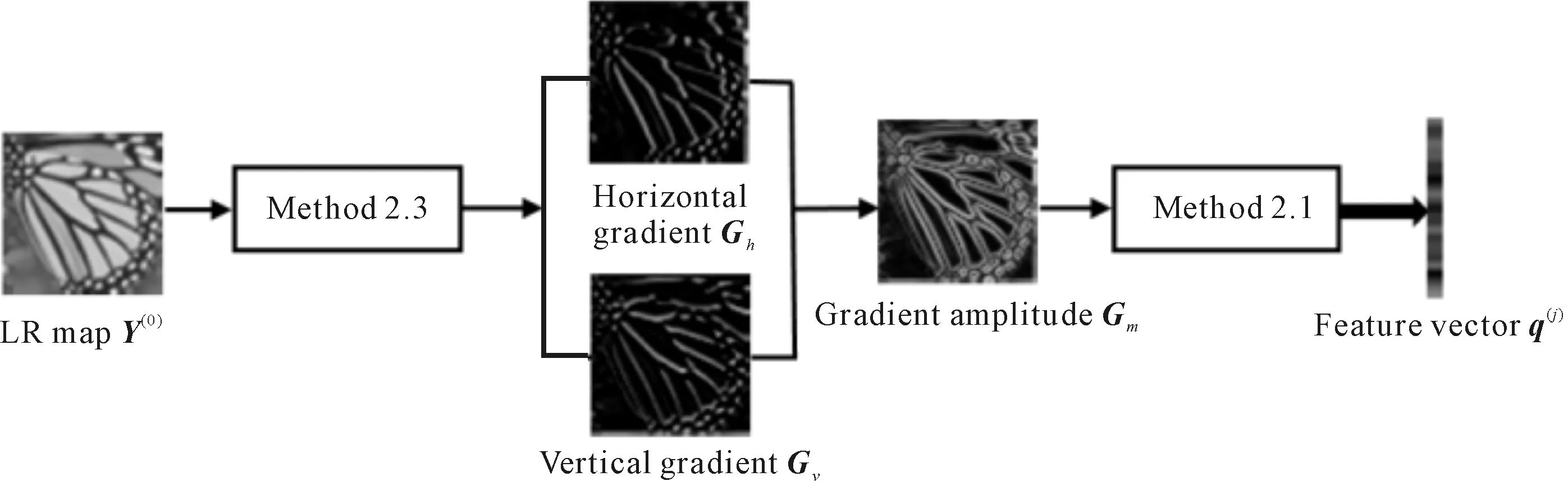
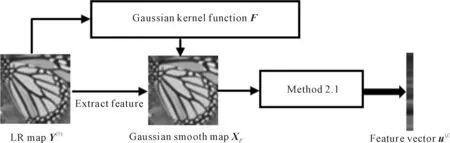
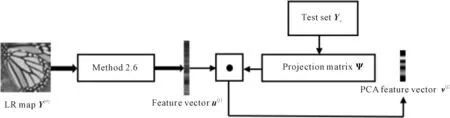
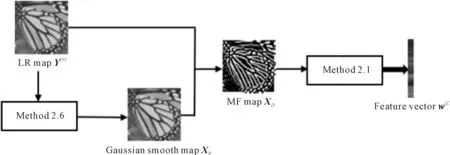
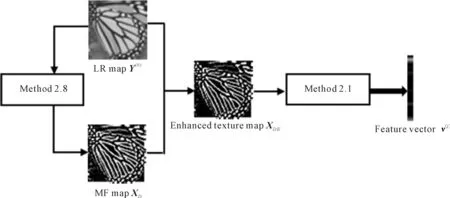
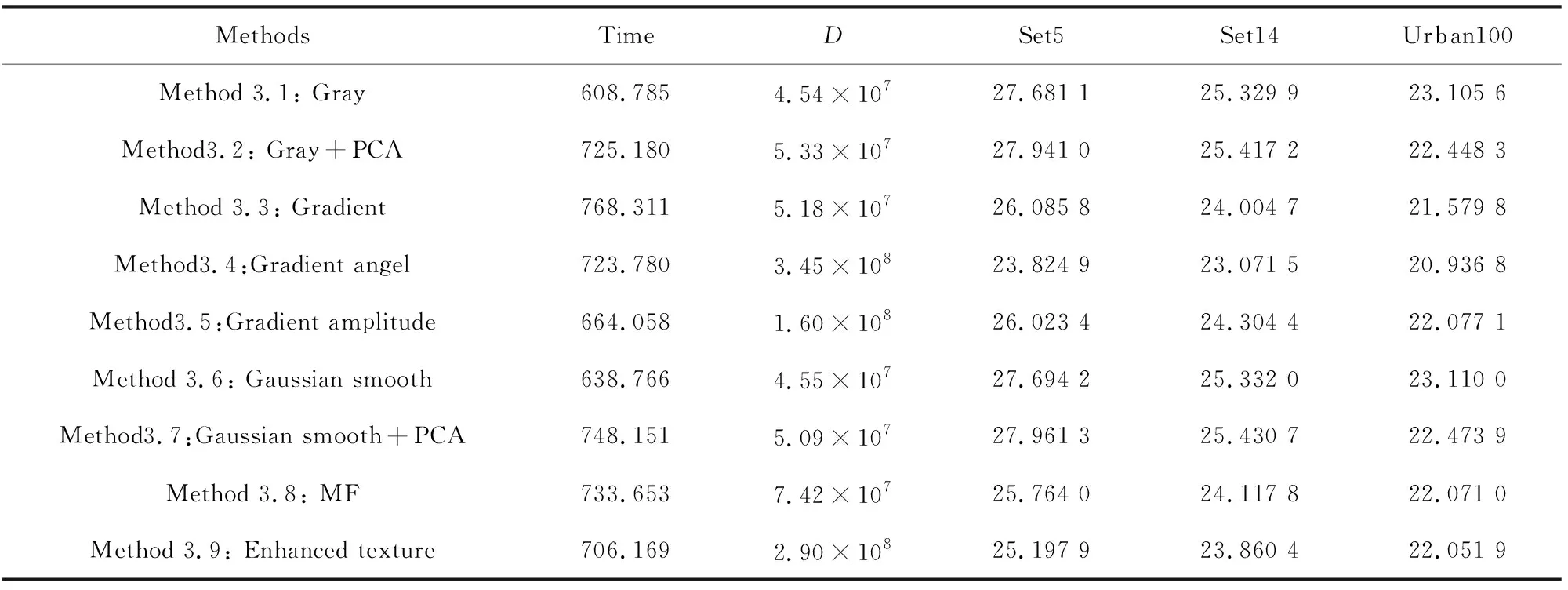
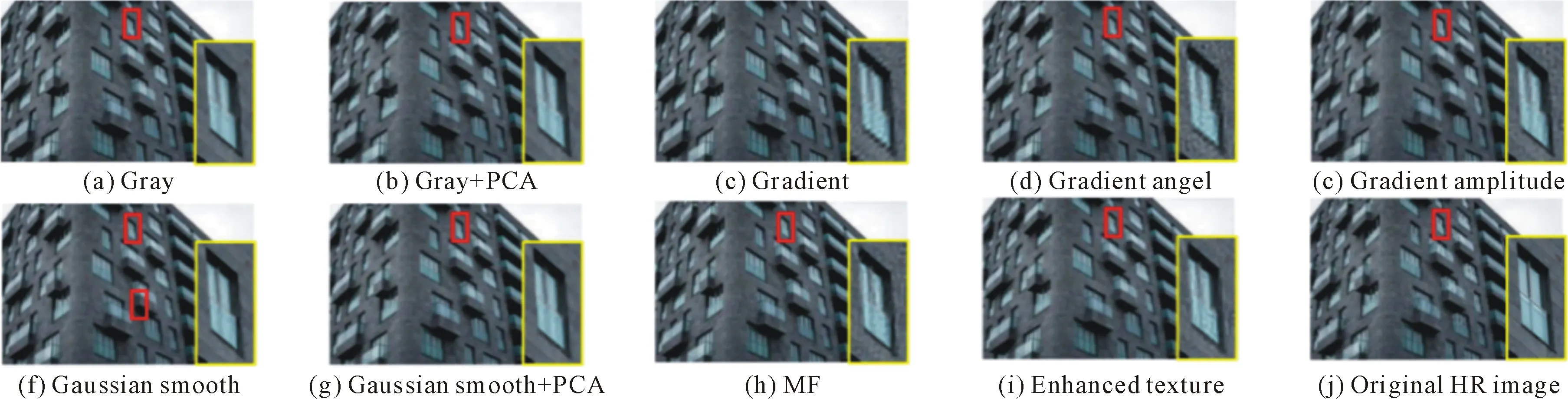
The data pyramid is generated by the method proposed by Zhang et. al[2](as Fig.1 shown). Denote the HR test image asX, and its size isM×N. Down sampleXto get imageX(-1), its scale issM×sN, where,s(0 Φ={X(0),X(-1),…,X(-(L-1))}. Then, a LR pyramidΨis generated byΦ. Up sampleX(-κ)to get imageY(-(κ-1))asκth level image ofΨ, where,κ=1,2,…,L. The up sampling factor is 1/s. Fig.1 The flowchart of feature extraction methods The gray pixel value which is easily extracted is widely used in image processing as intuitive image information. Though this feature is not innovation, we aim to describe the details of the feature matching process in this section. The first method uses gray pixel value to do the patch matching. Fig.2 shows the process of generating grayscale features. Fig.2 The gray pixel value extraction method Euclidean distance betweenα(j)andβ(i)is calculated by the following formula: (1) Finally, the mean square errorDbetween the selected HR training patches and the corresponding HR test patches should be calculated to assess selection quality. The mean square errorDis expressed as follows: (2) In the following, we only describe the feature extraction process in details. The method to assess selection quality is the same as the method described in this section. The PCA method is commonly used in dimensional reduction. It preserves the main data while reducing the dimension of data. In image processing, it can reduce the image feature redundancy and noise, and also is helpful to reduce time cost. Fig.3 shows the process of generating the PCA feature vectors. Fig.3 Gray feature + PCA method The gradient contains the pixel value variety information of an image. Many existing algorithms have used gradient to recover missing details in HR images[6,14]. Fig.4 shows the process of generating gradient features. Firstly, we produce the gradient maps (contain horizontal gradient maps and vertical gradient maps) of the LR pyramid by the following formulas: Gv=[-1, 0, 1]T*X, (3) Gh=[-1, 0, 1]*X, (4) where,Gvis the vertical gradient map of the imageX,Ghis the horizontal gradient map of the imageX, [-1, 0, 1]Tis the one-dimensional gradient operator in the vertical direction, [-1, 0, 1] is the one-dimensional gradient operator in the horizontal direction, and “*” is convolution. (5) Fig.4 The gradient feature extraction method The gradient angle represents the statistics of the gradient direction. The patches which have the similar gradient angle can be considered as the texture with the similar direction. Besides, compared with the method described in Section 2.3, the gradient angle has lower dimension. Fig.5 shows the process of generating gradient angle features. The gradient angleθexpression formula is as follows: (6) (7) The LR test set can be expressed as: H=[e(1),e(2), …,e(N)]. (8) Fig.5 The gradient angle feature extraction method Gradient amplitude shows whether the patch is a smooth patch or a texture patch. The gradient amplitudeGexpression formula is: (9) Fig.6 shows the process of generating gradient amplitude features. The horizontal and the vertical gradient map are obtained by the method described in Section 2.3. The gradient amplitude mapGmis obtained by using the formula (9). We useGmto get the LR test set by the method described in Section 2.1. Thejth feature vector of LR test set is regarded asq(j). TheNfeature vectors in the LR test set form matrixQ=[q(1),q(2), …,q(N)]. Fig.6 The gradient amplitude feature extraction method Some LR images contain noise which greatly disturbs the patch matching accuracy. Therefore, we use the Gaussian filter to reduce noise. The Gaussian smooth imageXFis obtained by the following formula: XF=F*X, (10) Firstly, the Gaussian smooth feature mapXFis produced by formula (10). We useXFto get feature vectors of the LR test set by the method described in Section 2.1. Thejth feature vector of LR test patch is regarded asu(j). The feature vectors in the LR test set form matrixU=[u(1),u(2), …,u(N)]. Fig.7 The Gaussian smooth feature extraction method We also use PCA to reduce dimension of the Gaussian smooth image, which can further avoid the effects of noise on image processing, and reduce computation time complexity. Fig.8 shows the process of generating PCA of Gaussian smooth feature vectors. The PCA project matrixψis produced by the method described in Section 2.2. Thejth Gaussian smooth patch of PCA feature vectorv(j)is produced by the following formula: v(j)=ψu(j). (11) The feature vectors in the LR test set form matrixV=[v(1),v(2), …,v(N)]. Fig.8 Gaussian smooth feature + PCA method The MF components contain basic edge structures of the image[7]. The MF feature mapXDis as feature map, which is obtained by the following formula: XD=X-XF. (12) Fig.9 shows the process of generating MF features. We obtain the Gaussian smooth mapXFby the method proposed in Section 2.6, and use formula (12) to get MF mapXD. Then, we useXDto get feature vectors of the LR test set by the method described in Section 2.1. Thejth feature vector of LR test set is regarded asw(j). TheNfeature vectors in the LR test set form matrixW=[w(1),w(2), …,w(N)]. Fig.9 MF feature extraction method We found that the LR image contains main step edges of the HR image, but they are not as sharp as HR image. We consider that if we can enhance the step edges before patch matching, the matching quality may be better. Since the absolute value of MF component can show step-edge positions[7], we utilize them to produce features. The enhanced imageXDEis obtained by the following formula: XDE=X·|XD| (13) where,XDis produced by the method described in Section 2.8. Fig.10 shows the process of generating enhanced texture features. Firstly, we obtain the MF feature mapXDand use formula (13) to get the enhanced texture map. Then, we use the map to get feature vectors of the LR test set by the method described in Section 2.1. Thejth feature vector of LR test set is regarded asν(j). TheNfeature vectors in the LR test set form matrixΝ=[ν(1),ν(2), …,ν(N)]. Fig.10 Enhanced texture feature extraction method We use Set5, Set14, and Urban100 as HR test images which are obtained from the code package of[15]. Since Urban100 only contains buildings, we only use the first 20 images in Urban100 for testing. The magnification factor is set as 4. Bicubic-interpolation method is employed to up sample or down sample in feature extraction process. The patch size is 5. The dimension of PCA feature vector is 10. We use the peak signal to noise ratio (PSNR) to measure the quality of output images. We did two types of experiments. The first one is to assess the quality of patch matching. The details of process are described in Section 2. The second one is to test these features on self-learning algorithm based on NE[16-17]. Tab.1 showsDvalues of the first experiment, the PSNR values and the time cost of the second experiment. From the table, we can see that PCA dimension reduction method can improve the accuracy of patch matching. However, since the dimension reduction process takes time, the operating speed is not improved. Tab.1 The cost(s) and average error values for matching of different features and the average PSNR(dB) of Set5, Set14, Urban100 Fig.11-Fig.14 show the visual quality. The topic of these images includes face, building, chips and license plate. From these figures, we see that method described in Section 2.6 and method described in Section 2.7 both use the Gaussian filter to remove noise, and employ the Gaussian smooth feature or its dimensional reduction version to reconstruct the HR image. The result images of two methods are clearer than others. We can see that method described in Section 2.3 and method described in Section 2.5 bring artifacts in smooth areas. This indicates that gradient is not a proper feature for patch matching, no matter using gradient or its amplitude. Although we consider that two images which have similar gradient angle may be similar, method described in Section 2.4 has more artifacts than method described in Section 2.3, which shows that the gradient angle is not suitable for patch matching. It is obvious that MF feature extracted by method described in Section 2.8 and its enhanced version calculated by method described in Section 2.9 are unsuitable for patch matching. Method described in Section 2.1 and method described in Section 2.2 both use gray value feature or its dimensional reduction version, the quality of the result images using these two methods are slightly worse than that obtained with Gaussian smooth features. We can see that the quality of outputs of the Set5 and Set14 data sets is not affected after using the PCA method to reduce the dimension, but in Urban100, the quality of images obtained by using PCA dimension reduction features is worse than that obtained by directly using features. This may be due to the fact that using the PCA method does not obtain better matching patches for the image with highly repetitive structure. Fig.11 The baby image results obtained by extracting different image features Fig.12 The building image building results obtained by extracting different image features Fig.13 The chip image results obtained by extracting different image features Fig.14 The plate number image results obtained by extracting different image features This paper proposes some feature extraction methods on self-learning SR based on NE. Some of methods aim at reducing noise, such as method described in Section 2.2 and method described in Section 2.7, some focus on enhancing step edges, such as method described in Section 2.3, method described in Section 2.4 and method described in 2.5, and some try to generate nonlinear feature by using linear feature. Experimental results show that different features can produce different SR outputs. According to comparison, PCA of Gaussian smooth feature has the best SR result in Set5 and Set14. In Urban100, Gaussian smooth feature obtains the best SR result. Although we have proposed several novel feature extraction methods, they still have limitation of solving one-to-many problems. With the development of SR research, we will propose more and more feature extraction methods to get better SR results.1.2 Building data sets
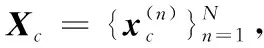
2 Feature extraction methods
2.1 Gray pixel value

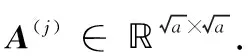
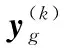
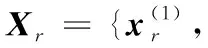
2.2 Principal component analysis (PCA) method
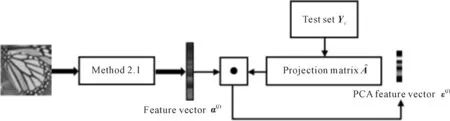
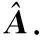
2.3 Gradient
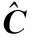

2.4 Gradient angle
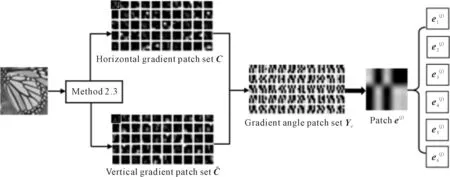
2.5 Gradient amplitude
2.6 Gaussian smooth
2.7 PCA of Gaussian smooth feature
2.8 Midfrequency (MF) feature
2.9 Enhanced texture
3 Experimental results



4 Conclusion
