数学排队论模型在通信网中的应用研究

2018-12-23尹皇皓

科技与创新 2018年1期

关键词：通信网排队现象

尹皇皓

（大连市第二十四中学，辽宁大连 116000）

数学排队论模型在通信网中的应用研究

尹皇皓

（大连市第二十四中学，辽宁大连 116000）

排队论是一种数学理论和方法，它是运筹学的一个分支，又称随机服务系统理论。排队是生活中的一种常见现象，渗透人们生活的方方面面。主要论述了排队论在通信电网中的应用。

排队论；通信网；平衡模型；电话损失率

排队论实际上是一种服务系统理论。人们在日常生活中会碰到大大小小的排队问题，比如排队选购商品、排队结账、排队等待电梯等。1909年，丹麦数学家A.K.埃尔朗在解决自动电话设计问题时，首先提出了排队论的理论体系。埃尔朗以热力学统计平衡理论为基础，开创性地建立了电话统计平衡模型，并提出了著名的埃尔朗电话损失率公式。埃尔朗的理论研究影响很大，不仅仅解决了电话系统的设计问题，他的理论还被应用于计算机网络、生产、服务管理、运输、军事等多个领域。计算机近几年的发展十分迅速，它的崛起不仅健全了通信系统，还促进了排队论的理论研究和应用。

1 通信网与排队论概述

以往，分隔两地的人通过信件通信交流，送信过程长且易丢失。随着通信网的建立，可以让分隔很远的两个用户迅速实现交流沟通。通信网就是分处异地的用户之间传递信息的系统，但只是点与点之间的沟流交通，不能称为通信网，这只是通信的基本形式。通信网是由许多的传输系统交换后，按照几何拓扑学组合在一起。排队论可以用来分析通信网中流量的使用情况。通信网内的流量数据十分庞大，用排队论分析时并不简单，但排队论可以精准地分析特点的节点、路径上的流量。因此，研究人员通常应用排队论指导通信网的流量设计。排队论又称随机服务系统理论，就是研究随机聚散现象、服务系统工作的数学方法。1909年，丹麦数学家A.K.埃尔朗在解决自动电话设计问题时，首先提出了排队论的理论体系，他提出的著名的埃尔朗电话损失率公式，不仅解决了电话系统的设计问题，对后世也有很深远的影响，后世数学家基本沿用他的公式研究排队论。20世纪50年代，堪道尔（D.G.Kendall）系统地研究了排队论，他受到了概率论中马尔可夫链的研究启发，进一步完善了排队论的理论研究，1951年，他提出用A表示顾客到达时间分布，B表示服务时间的分布，C表示服务机构中的服务台的个数的排队分类。堪道尔的研究扩大了排队论的应用范围，计算机网络、生产、服务管理、运输、军事等多个领域均有涉及，其中，通信领域应用最多。实际需求诞生了排队论，也会影响排队论的发展。以下将主要论述排队论如何提高通信领域的商业价值。

2 排队论在通信网中的商业运用

排队是生活中的一种常见现象，渗透了人们生活的方方面面。人们日常中会碰到大大小小的排队问题，比如排队选购商品、排队结账、排队等待电梯等。人们的生活需求孕育了排队论，也必然影响排队论的发展。在很多领域都可以看到排队论的应用。本文重点叙述排队论在通信网中的商业运用。通信网是一个非常庞大的系统，里面也充斥着不少类似排队的问题，比如电话占线问题，如果电话用户联系其他用户时，中断线都显示占用状态，则该用户就不能进行正常的通信，必须等待。排队论是一种分析通信网的数学方法，但通信网内的信息数据过于庞大，综合分析的难度很大。数据由存储到转发的过程也是一个类似排队的过程。数据并不能直接传播，到达节点时也需等待处理。像这种需要等待处理的现象都是类似排队的现象，不同的是，我们的肉眼不能直接观察到这些问题。这种现象不止存在于通信领域，科学研究的很多领域都存在排队现象。如图1为多队多服务台系统。

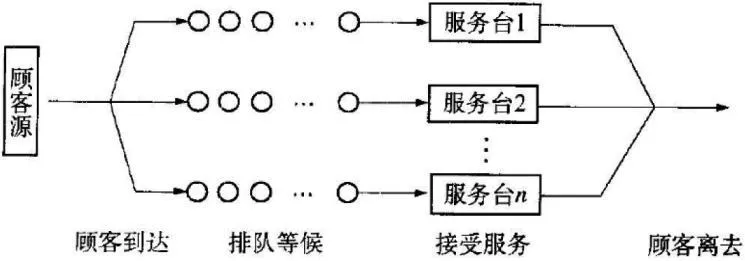
图1 多队多服务台系统

排队论实际上是一种服务系统理论，因此，都存在被服务者和提高服务者。我们可以把通信网中要求服务的人称为客户，接受服务要求并提供服务的一方称为服务机构（机器设备、信息网等），中继线、信道等类似接收、传达服务信息的设备可以形象地比喻为服务窗口。通信网运行时，客户提供要求的时间、数目都是不确定的，因此，提供服务的时间也是不确定的。客户数目、要求未知，但是提供服务的设备有限，当客户要求超出服务设备所能承受的范围时，客户就必须等待，这就是排队现象产生的原因。服务设备的数量与客户需求之间的关系在一定程度上可以决定服务的质量。如果客户要求超出服务设备所能承受的范围，客户就需要排队等候，排队时间越长，不满意的程度越高；如果客户要求未超出服务设备所能承受的范围，排队现象就会减少，客户会比较容易得到满足感。排队的规则可以分为三类，按照服务设备的数量和客户使用服务设备的时间长短等划分为：①等待制。所有服务窗口、服务员都不能提供服务，客户只能按到达的先后顺序排队等待，有时会有插队现象。②损失制。客户排队等待时，失去耐心、有其他事情待进行等离去现象。③混合制。混合制即以上两种现象都存在。