多车型多车辆货车装载算法及应用

文/陈宏程 贾江鸣 崔志军

随着物流业发展，货车装箱的优化问题得到越来越多的重视。一般情况下，一批货物订单生成后，形成一个货物清单，货物装运需按清单顺序直接装车，货物大小不一，导致车辆空间不能有效使用。装箱问题是一个著名的多项式复杂程度非确定性（NP-hard）难题，直接求解有相当高的时间复杂度和空间复杂度。启发式算法是通过特定的搜索规则和搜索策略，在搜索空间中搜索最优解，被大量运用在解决复杂问题优化中。针对装箱问题的研究，目前大部分将装箱问题简化为单车型装载问题，有些简化为单车型单车辆装载问题，因此尽管这些模型取得了较好的理论研究进展，但仍难以适应实际问题中的多车型多车辆装载环境。

本文在启发式算法的选择上，模拟退火算法在解决复杂多目标问题上具有通用性、高效性，但其所得解的好坏受初始状态、温度函数等影响较大，降温快易陷入局部最优，降温慢则求解过程极其缓慢；蚁群算法缺点同模拟退火算法，求解过程受初始参数影响较大；遗传算法所得解的好坏，主要依赖于遗传代数和解组规模，若所得解不能让人满意，只需增加解组规模和遗传代数，与模拟退火算法与蚁群算法相比具有一定优势。本文选取遗传算法并对其进行改进，降低了解的不稳定性，利用遗传算法高效地在解空间中搜索优解序列，通过三空间装箱原则确定序列可行解，运用python语言实现了多车型多车辆装箱问题的优化算法。

随着物流业的发展，货车装箱的优化问题得到越来越多的重视

一、 问题描述

1.装载问题描述

区域物流配送中心的装载问题可以被描述为：各订单需求的货物被装入一定规格的瓦楞纸箱中，将这些具有不同规格的纸箱按照一定的规则装入到不同型号且分别具有不同载重和容积限制的货车内，在满足车辆运力限制的情况下，选取最优车型装载货物，在满足货车容积约束的条件下，确定各货物在车厢内的摆放位置和放置状态，以使运输总成本最低。模型具体参数如下：已知有n件纸箱（规格：长li、宽wi、高hi、质量gi，其中i = 1,2, ... ,n）要装到m辆车内（已知有四种车型，各型号车辆长Lj、宽Wj、高Hj、最高载重Gj、出车费用Sj等为固定值，每种型号的车辆数不限，其中j= 1,2,3,4）。

2.目标函数和约束条件

（1）目标函数

装载问题的常见目标函数如下：①载重量利用率最大；②空间利用率最大；③面积利用率最大；④运输总成本最低。

本文目标为多车型多车辆的最优装载规划，以上单一目标无法比较不同解的优劣，故以车厢的综合运输总成本最低作为目标函数。模型的目标函数为：

式(1)中Sj为j车型出车费用，numj为j车型出车数量。

（2）约束条件

装载问题常见的约束条件：方向约束、装配优先级约束、底面积约束、长宽高约束、体积约束、载重约束、承载能力约束和稳定性约束。本例中多为轻小件货物，故载重、承重能力约束性较弱，因此本文主要考虑约束长、宽、高约束和体积约束等。模型的约束条件为：

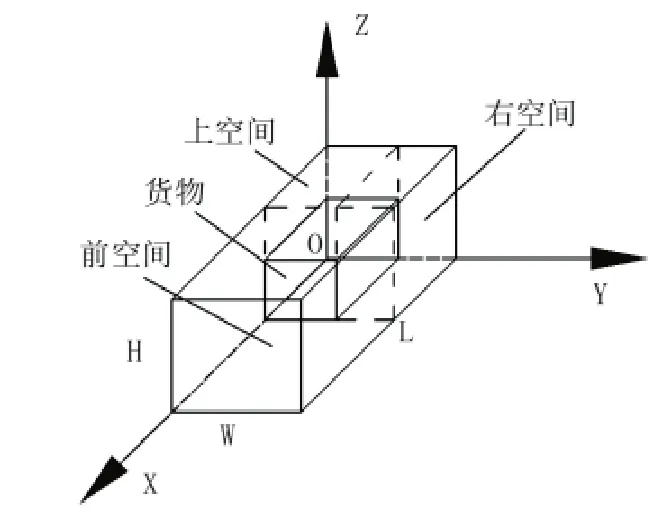
图1：笛卡尔坐标系

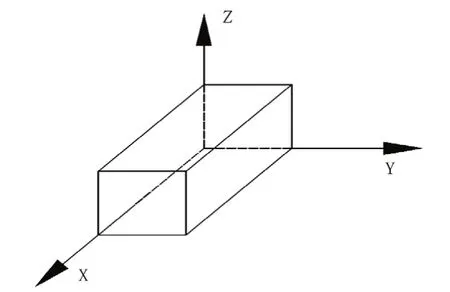
图2：子空间划分示意图

式（2）、（3）、（4）表示装入j车型车厢货物的长、宽、高均不超过货车车厢的长、宽、高，式（5）表示装入j车型车厢的货物总体积不超过货车车厢体积。

（3）模型假设

结合本例实际情况给出以下假设：

①车厢与货物外形均视为规则矩形；

②货物向上放置，可水平旋转；

③货物挤压不变形；

④货物无优先级；

⑤忽略货物对车厢稳定性影响。

二、模型求解及算法分析

在装箱顺序上，许多知名学者进行了深入研究。本文利用改进算子的遗传算法结合三空间装箱原则，在装箱顺序和车辆分配维度下求解最优装载方案。

1.装箱规则

本文采用笛卡尔坐标系，如图1。为使装载率尽可能高，本文考虑定位原则、空间分割与空间合并等几个启发式原则。

（1）定位原则

定位原则是货物采用“金角银边草肚皮”的占角策略，货物以左前下角坐标为基准向坐标原点聚集摆放。

（2）空间分割原则

为了保证货物在装载过程中不存在“悬空”现象，本文对空间采用三空间分割法。George和Robinson最先提出了三空间划分原则，当货物放入车厢后，该车厢被分割成前、右、上三个子空间。每个子空间在继续装填货物过程中，放入货物后同样被分割为三个子空间，如此循环往复直至无法装下。子空间划分，如图2。

（3）空间合并原则

子空间划分过程中会不断地出现小空间，过多的小空间不利于货物的继续装载，可通过空间合并形成新的较大空间。合并过程，如图3 (a)-(c)。

2.多车型装载算法

图3：左右/前后/上下空间合并

装载算法可分为在线和离线两种：在线算法是先到的箱子先装箱，而离线算法是在所有物品就绪的情况下再进行装箱。结合发货情况，本文采用了离线装箱中的FFD装载算法。为使算法适应多车型多车辆装载模型，本文在FFD装载算法的基础上添加了车型的选择，装载示意图，如图4。

图4为多车型选择—装载过程示意图。

本文在装载算法中添加参数“最优性价比”，流程通过“最优性价比”对车型进行定量筛选。“最优性价比”公式如下：

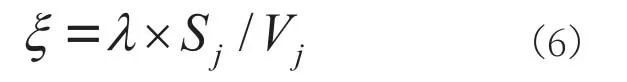
式中ξ为“最优性价比”，λ为车辆装载率，Sj为j车型的固定出车费用，Vj为j车型的车厢体积。

3.遗传算法

遗传算法GA是模拟生物进化汰弱留强过程的一种搜索最优解的进化算法。编码P对应货车装载问题中的一种装载方案，群体M为装载方案的集合。适应度函数对应装载问题中的优化目标，个体适应值越高，其编码的装载方案越优秀，被保留下来的几率越大。

（1） 编码/解码

待装货物的装载顺序是由启发式原则确定的，直接采用装箱顺序作为个体P的编码。初始编码顺序由程序随机得到。

（2）适应度函数

适应度函数为目标函数运输总成本的倒数。为了更好地表达解的优劣，添加最后一辆车的空间装载率最低（折算成车辆使用费用）来辅助表示适应度函数。首先，在装载结果中，方案显示车型与车辆数目都相同时，仅车型费用乘以车辆数目无法准确表达装箱排序的优劣，增加将最后一辆车的空间装载率最低作为指标以辅助判别最优方案，可以加快算法的收敛；其次，最后一辆车空间利用率最低可以为临时/紧急订单货物的装载提供便利，该类货物可不通过计算直接置于最后一辆车，节省计算时间。

适应度函数定义如下：

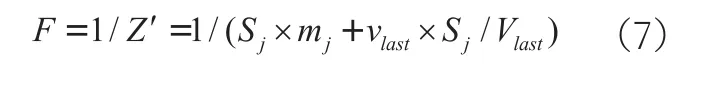
图4：多车型选择—装载过程示意图

图5：交叉操作

表1：车辆数据表

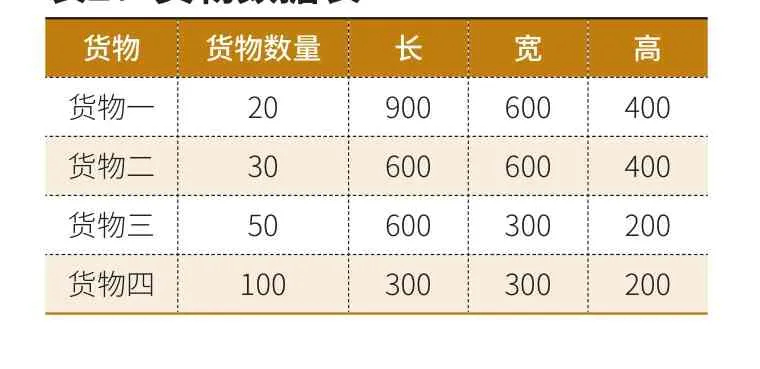
表2：货物数据表

式中Vlast为最后一辆车装载货物总体积，Vlast为最后一辆车装载体积。

（3）选择操作

本文采用轮盘赌作为选择方法。群体M中父代群体为{P1，P2，P3，…，PM}。选择操作步骤如下：

①计算个体被选择的概率，并计算出个体的累积概率；

②生成一个0～1随机数，若随机数在个体累积概率区间之间，则该个体被选中；

③重复第a、b步，得到M个个体组成新群体{P’1，P’2，P’3，…，P’M}。

（4）交叉操作

交叉概率为Pc，交叉群体为{P’1，P’2，P’3，…，P’M}。交叉步骤如下：

①选择相邻父代P’1、P’2进行交叉，生成一个0～1随机数，若随机数大于Pc，则不交叉；若随机数小于等于Pc，则对P’1、P’2进行交叉操作；

②在[1，n]之间生成2个随机整数a和b（a＜b）作为交叉点，交换P’1、P’2位于a和b之间的基因段，如图5。

③重复a、b步骤直至个体交叉结束，得到新群体{P’’1，P’’2，P’’3，…，P’’M}。

（5）变异操作

变异概率为Pm，变异群体为变异步骤如下：

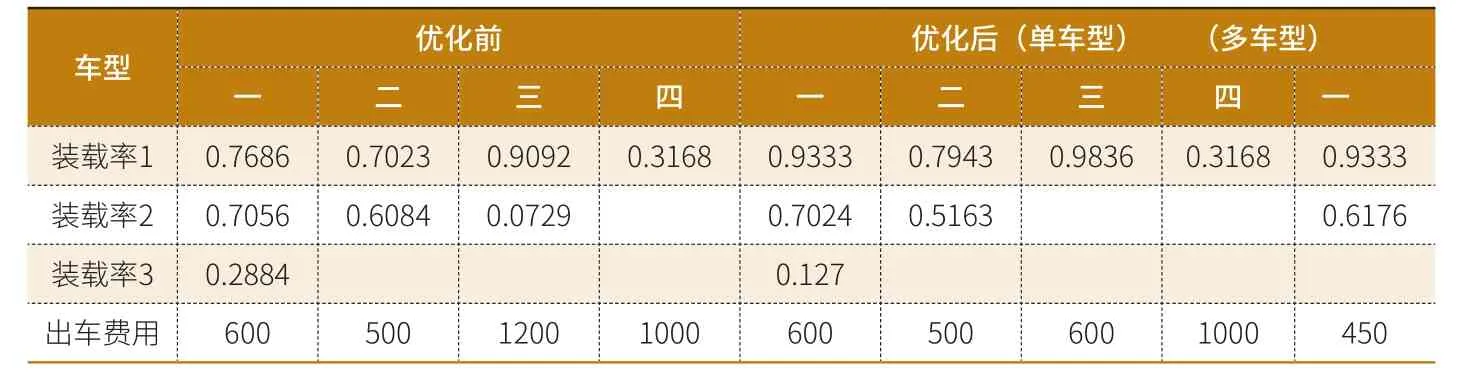
表3：优化结果对比分析表

图6：多车型优化分布表

①选择父代P’’1进行变异，生成一个0～1随机数，若随机数大于Pm，则不变异。若随机数小于等于Pm，则对P(2)1进行变异操作；

②在[1，n]之间生成2个随机整数a和b（a＜b）作为交叉点，交换P’’1位于a和b上的基因；

（6）逆序操作

逆序概率为1，即所有个体都进行逆序操作。逆序操作会对比逆序前后适应度函数，若逆序后适应度比逆序前适应度更优，则保存该逆序操作结果，否则仍保存原先序列。具体操作步骤如下：

①在[1，n]之间生成2个随机整数a和b（a＜b）作为逆序点，将P(4)1位于a和b上的基因逆转排序；

（7）择优保存策略

择优保存策略是为了避免父代中的优秀个体在遗传迭代的过程中消失。其步骤为：

①计算父代群体{P1，P2，P3，…，PM}中所有个体的适应值，找出父代中适应值最高的那个个体，即最优父代（其适应度值为Fmax）；计算子代群体中所有的个体适应值，找出子代中适应值最小的那个个体，即最劣子代（其适应度值为F(4)min）；

三、算例分析

1.案例数据

为更好地对比算法优劣，本文选用行业内的一些基础数据，在保证数据量基本相等的前提下，把货物尺寸进行改动，以适应实际装载问题；其中，第一辆车的大小与原对比数据中的车型大小一致。具体数据如下：见表1、表2。

表中出车费用单位为元/辆，长、宽、高单位为mm，货物数量单位为件。

2.测试结果

算法的各项参数如下：

群体规模M 80

遗传代数GEN 500

交叉概率Pc 0.9

变异概率Pm 0.05

对上述案例数据以及各项参数进行算法求解，得到结果，如下表3。

运用多车型多车辆算法优化模型得到12组解，结果分布，如图6。

如图6试验数据表明，本算法的空间利用率平均分布在88.53%～93.33%之间，空间装载率可到93.33%。

3.优化结果分析

本文算法主要优势：

（1）本文提出的多车型、多车辆装载算法更适合应用于实际场景；

（2）本文的算法空间利用率可达到93.33%，与同类研究文献比较，本文的算法在空间利用率上存在一定优势；

（3）装载率只是评价装载方案优劣的一种指标，本文给出的综合运输成本指标更适合用于评价实际装载方案的优劣。

综上所述，本文装箱算法在空间利用率以及综合成本上均具有一定优势。

四、结语

本文对某区域物流配送中心运输问题的货车装箱方案进行了优化，给出了装箱优化算法，并进行了实例研究，通过实例数据对比结果可知，本文的装箱算法具有一定的成本和装载率优势。本文研究模型不足之处在于：该模型主要针对区域物流配送中心，运用范围较为局限，后期将对该模型进行改进，使其能够适应更多领域。