不同抚育强度对兴安落叶松林空间结构的影响1)
2018-12-21姜廷山王鹤智董灵波陈莹刘兆刚
姜廷山 王鹤智 董灵波 陈莹 刘兆刚
(东北林业大学,哈尔滨,150040) (国家林业局调查规划设计院) (东北林业大学)
在森林经营过程中,可以通过抚育间伐改善森林空间结构[1-6]。较为常用的森林空间结构指标,主要包括树种混交和树木竞争指数、树木空间分布格局。混交度由Gadow在1992年提出,汤孟平等[7]综合考虑空间结构单元中的树种隔离程度并引入树种多样性指数,提出了全混交度的概念。树木竞争分析中应用最为广泛的是Hegyi竞争指数、大小比数等。用于描述林木分布格局的指标,主要有聚集指数、角尺度等。惠刚盈等[8]对Ripley’L、双相关函数与角尺度方法进行了对比分析,发现角尺度在有效性和可行性方面比Ripley’L函数和双相关函数更强;Corral-Rivas et al.[9]比较分析了Clark & Evans指数、平均方位角指数、Ripley’L检验、角尺度等几种方法的性能,认为角尺度方法的分析灵敏度与Ripley’L检验相当。
森林空间结构分析比较是现代森林经理学的研究热点之一。森林空间结构的模拟研究是对森林结构分析描述的进一步扩展。由于树木生长周期长,导致经营措施短期内难以看出实践效果,模拟即成为预测森林空间结构与动态的重要手段。现阶段,森林规划模型求解方法主要有精确式算法和启发式算法两大类[10-12]。关于森林空间结构的研究,主要集中在空间结构指标选取与量化、空间结构分析、空间结构优化模型的建立等方面[13-19],但将样地模拟采伐与空间结构优化评价结合的研究较少。本文以大兴安岭天然落叶松林为研究对象,综合考虑非空间结构指数与空间结构指数,结合优化算法,模拟不同抚育强度对大兴安岭天然落叶松林林分结构的影响,进一步实现空间结构的优化,旨在为大兴安岭地区森林经营活动提供参考。
1 研究区概况
研究区域位于黑龙江省大兴安岭地区塔河县城西北部加漠公路线上的盘古林场。该场始建于1969年,隶属于塔河林业局,经纬度坐标为52°41′57.1″N、123°51′56.5″E,海拔230~1 397 m,属低山丘陵地貌。林场的营林面积为15.2万hm2,森林覆盖率高达88.9%。气候属寒温带大陆性季风气候,气候变化显著。地势西高东低,年降水量300~450 mm,相对湿度70%~75%。研究区植被类型丰富,分布不同土壤,以棕色针叶林土和草甸土为主。主要树种有兴安落叶松(Larixgmelinii)、樟子松(Pinussylvestrisvar.mongolica)、白桦(Betulaplatyphylla)、山杨(Populusdavidiana)、红皮云杉(Piceakoraiensis)、鱼鳞云杉(Piceajezoensis)等;灌木树种有兴安杜鹃(Rhodendrondauricum)、胡枝子(Lespedezabicolor)、红瑞木(Cornusalba)、杜香(Ledumpalustre)等。
2 研究方法
2.1 数据来源与处理
2013年在塔河林业局盘古林场分别设置1块100 m×100 m、2块50 m×50 m的天然落叶松林样地,3块样地均属于幼、中龄林。对样地内树木胸径≥5 cm的所有林木进行标号和检尺;树高使用超声波测高器进行测量,坐标采用相邻格网(10 m×10 m)进行调查。3块样地树种组成分别为7落3白-樟-云(L01,100 m×100 m);7落2樟1白-杨(L02,50 m×50 m);8落2白+云-樟(L03,50 m×50 m)。3块样地基本统计特征见表1。

表1 样地基本统计特征
2.2 指标的选取
评价林分结构可以分为用非空间结构和空间结构的指标。非空间结构可以考虑到林木直径大小的多样性,天然异龄林直径分布为倒“J”型,比正态分布的林分具有更高的林木直径大小多样性。异龄林株数按径阶分布可用(1)式负指数分布表示。
N=ke-ad。
(1)
式中:N为株数;e为自然对数的底;d为胸径;a为负指数分布结构常数;k为常数。
对(1)式进行回归分析,可得常数a和k值,并将a值与径阶距带入(2)式求得样地q值。
q=eah。
(2)
有研究表明,若q值在1.2~1.7范围内,则属于正常范围[20],而且q值在此区间内时越小,表明该林分的林分大小多样性越丰富。因此,在林分抚育间伐后,应使林分径阶分布的q值在该区间内。
本文中水平空间结构指标的选取,主要从林分竞争、空间分布格局、树种混交分布等角度考虑,这里直接选取大小比(U)、角尺度(W)、混交度(M)[21]、竞争指数(IC)[22]4个指数判断林分空间分布格局的合理性。从林分角度看,优化的目标是林分整体的大小比减小、角尺度趋近于[0.475,0.517]之间[23]、混交度增大、竞争指数减小,这样才能使林内竞争减小,单木分布趋近于随机分布,林分稳定性增加。考虑到单木生长空间林木未来发展趋势的重要作用,本研究继续引入开敞度指标:
(3)
式中:Ki为参照树i的开敞度;n为最近邻木株数;Dij为参照树i与最近邻木j的水平距离;Hij为最近邻木树高。开敞度可以划分为5个区间:(0,0.2]、(0.2,0.3]、(0.3,0.4]、(0.4,0.5]、(0.5,+∞),其对应的林木生长空间充足程度分别为严重不足、不足、基本充足、充足、很充足。相邻木距样木距离越远,相邻木树高越低,K值越大。这说明,开敞度不仅反映了光照的接收能力,同时也反映了营养空间的大小,经营目标使开敞度增加。
采用林层指数描述林分的垂直空间结构。根据国际林联(IUFRO)的林分垂直分层标准,以林分的优势高为依据把森林划分为3个垂直层,上层林木为树高≥2/3优势高、中层林木为介于1/3~2/3优势高之间的林木、下层林木为≤1/3优势高的林木。本次将调查地的森林分为3个垂直层,树高≥12.0 m为上层、6.0 m≤树高<12.0 m为中层、树高<6.0 m为下层。
(4)

计算上述空间结构指数时,采用缓冲区方法对样地进行边缘校正,即由固定样地的每条边向固定样地内部水平距离5 m范围作为缓冲区。除缓冲区以外的部分称为校正样地,计算各项指标时,校正样地的树木是对象木。3块样地皆为幼、中龄林,故采用株数强度作为模拟采伐强度,设置了4个不同采伐强度,即轻度(10%)、中度(20%)、强度(30%)、极强度(40%)。
2.3 目标函数的构建与约束
鉴于上述各指标范围、单位及方向均显著不同,因此采用乘除法构建林分优化目标函数;同时,根据林分生长、优化目标等设置必要约束条件。具体如下:
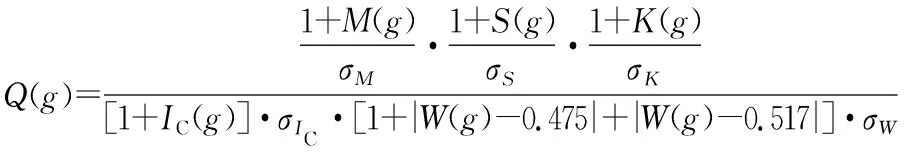
(5)
满足:
q(x)≥q1;
(6)
q(x)≤q2;
(7)
N=Ng(10%、20%、30%、40%);
(8)
S(g)>S0;
(9)
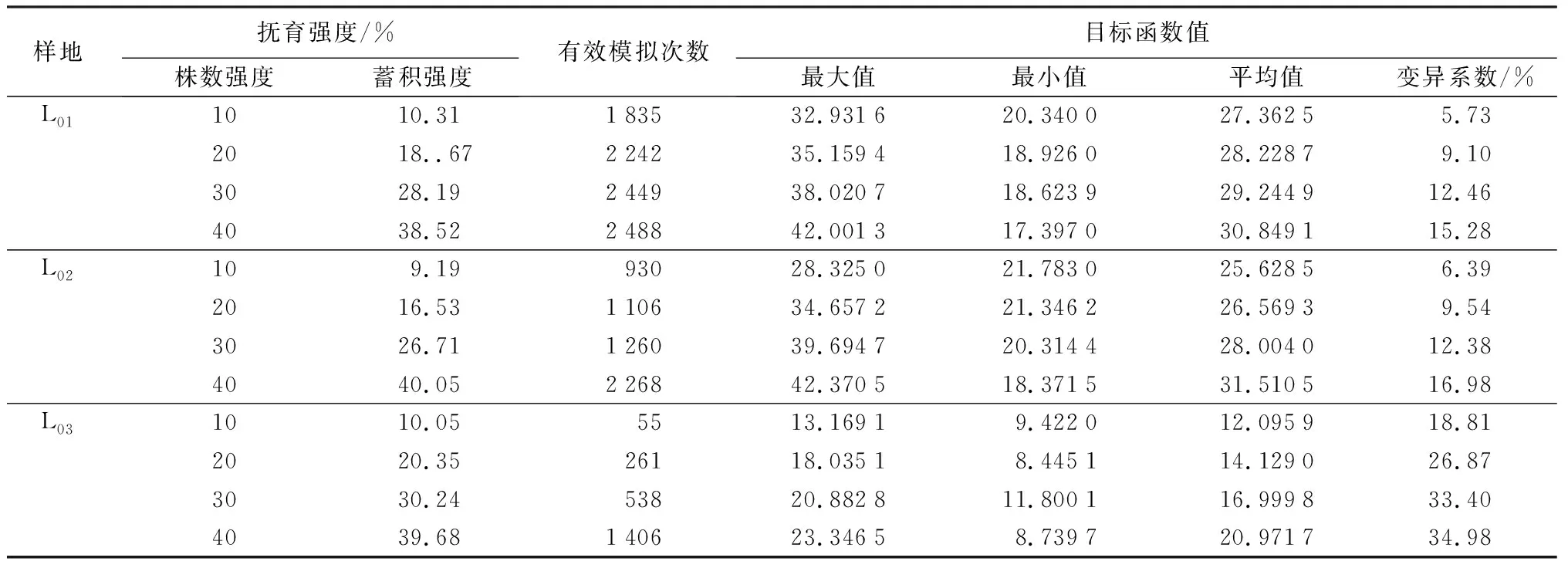
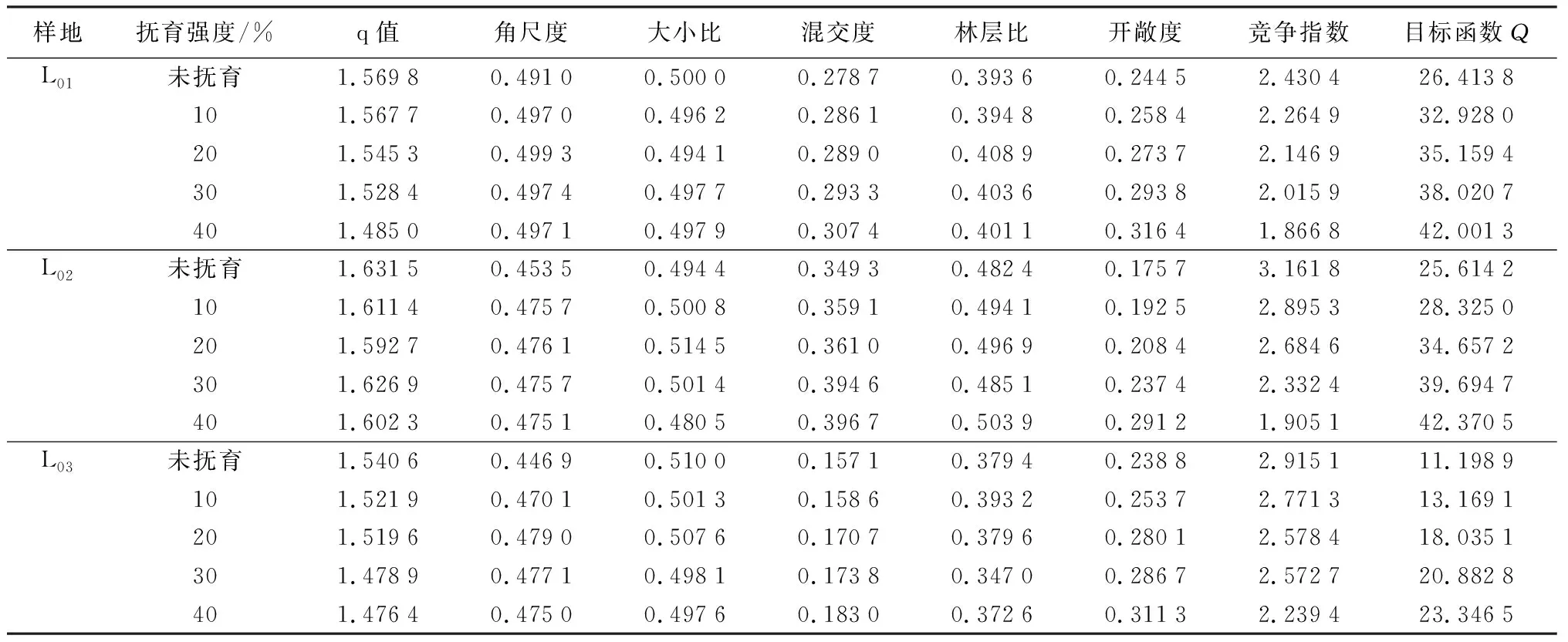
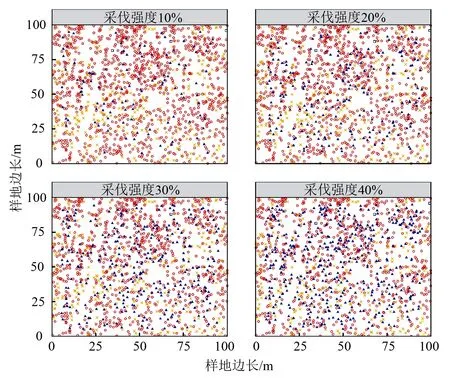
IC(g) (10) D(x)=D0; (11) M(g)>M0; (12) K(g)>K0; (13) 0.475 (14) 式中:M0、S0、K0、IC0分别为林分采伐前的混交度、林层度、开敞度、竞争指数;M(g)、S(g)、K(g)、IC(g)、W(g)分别为林分采伐后的混交度、林层度、开敞度、竞争指数、角尺度;σM、σS、σK、σIC、σW分别为以上5个指标的标准差;q(x)为伐后q值;N为人为设置的4种采伐强度;D为林分径阶数。公式(6)、(7)是林木大小多样性约束,林木大小多样性可用径阶多样性和株数按径阶的倒“J”型分布描述,q值一般在1.2~1.7之间;公式(8)用于控制株数采伐强度,按照国家抚育间伐规程,本研究模拟4种不同的株数强度,即轻度(10%)、中度(20%)、强度(30%)、极强度(40%);公式(9)为林层指数约束,该值越大,说明林分垂直结构多样性越高;公式(10)为竞争指数约束,经营的目标是减轻林内竞争情况;公式(11)为径阶约束,表示采伐前后径阶数不变;公式(12)是混交度约束,经营方向应使林分混交度增大;公式(13)为开敞度约束,保证林分内树木生长空间开阔;公式(14)为角尺度约束,保证林木分布为随机分布。 模拟采伐时采用蒙特卡罗模拟的方法。蒙特卡罗方法属于启发式算法的一种,主要用来预测复杂趋势和事件的数字模型,而这种模拟主要取决于可靠的无穷尽的随机数目来源。蒙特卡罗模拟的意义在于简化高维积分运算,降低涉及高维积分算法的时间复杂性。 以样地L01为例,将样地林木按2 cm径级进行分组统计,径阶D0=18 cm,样地内林木多数为中小径阶林木。林分株数对数(lnN)与径阶(D)的关系见图1。拟合得出式(1)中的参数a=0.225 5、径阶宽度h=2 cm。把a和h带入式(1)中计算得样地q=1.569 8,介于1.2~1.7,采伐时注意约束q值处于合理范围内。 图1 株数对数与径阶的关系 由表2可见:L01样地呈明显的随机分布,而L02、L03样地则更接近于均匀分布。3块样地大小比数,由大到小依次为L03、L01、L02,但其值差异较小,且大小分化程度均处于中庸状态。从样地平均竞争指数看,各样地竞争状况则出现明显差异,竞争指数由大到小依次为L02、L03、L01,表明林分单木营养空间L02样地最小、L01样地最大,且大小比数和竞争指数2指标在反映林分竞争状况时表现出一定程度的差异,这是由于在林分尺度下,平均竞争指数相对平均大小比数指标更为灵敏,即更能反映林分整体的竞争情况,这一结论在后文有更详细的说明。样地混交情况,混交度由大到小依次为L02、L01、L03,但总体看,林分混交程度偏低,这主要是由于研究对象均为落叶松林,树种组成结构比混交林相对简单。林层比反映样地垂直分层情况,L02样地垂直分层最好,L01样地比L03样地稍好,即L02样地乔木垂直多样性最高,但整体看,各样地乔木垂直多样性均偏低。从各样地初始空间结构指标值看,L03样地空间结构情况处于相对劣势状态。L02样地的q值相对偏高,但总体看,3块样地直径分布q值均处在合理区间[1.2,1.7],说明各样地林木径级结构处于合理状态,后期进行模拟调整结构时需考虑保持该结构的合理性。 表2 各样地采伐前林分结构参数 编制R程序,计算样地各项空间结构指标,并代入目标函数;采取蒙特卡罗启发式算法进行模拟,对样地树木随机采伐,分别以10%、20%、30%、40%模拟采伐强度模拟5 000次。模拟次数对于结果的准确性非常重要,模拟次数越多,模拟结果越能接近实际结果;但实际上次数过多,会浪费大量的人力物力,本研究经过前期的多次模拟测试,选择5 000次模拟次数,能够达到较好的模拟效果。其中,在选取到最优采伐方案时,随着模拟采伐强度的增加,目标函数输出值以及有效输出次数均有逐渐递增的趋势,且在模拟采伐强度为40%时,目标函数均值达到最大(见表3),即该强度下,林分结构平均状态最佳。而函数输出值的变异系数也随着采伐强度的增大呈现递增趋势,表明采伐强度增大时,目标函数输出值波动会随之增加,因此,在较高强度采伐时,应该考虑更为谨慎的采伐方案。同时,L03样地的模拟有效输出次数(1 406)以及优化函数均值(20.971 7)均比其他2块样地低,这是由于L03样地初始条件比另外2块样地较差的原因。 表3 各抚育强度模拟结果 由表4可见:3块样地在选取最优采伐方案过程中,其角尺度值具有不同程度的优化,且均在20%采伐强度时达到最大值;随后,随着强度的继续增加有一定的减小趋势;但总体看,在各采伐强度梯度内筛选的最优采伐方案中,各样地角尺度值仍处于随机分布范围内。李建等[24]认为,当采伐强度过大时,林分内林木的分布将接近于均匀分布,这与本研究中角尺度值出现减小趋势一致。 大小比数总体趋势降低,但变化幅度较小,处于0.480~0.515范围内浮动。这是由于大小比是空间结构单元内对象木的竞争关系指标,对于林分整体的竞争关系描述并不理想,竞争指数能更好的反映林地内竞争状况。这与周梦丽等[25]、陈科屹等[26]研究结果一致。 样地混交度逐渐增加,3块样地的混交度值均在采伐强度为40%的最优采伐方案时达到最大(0.307 4、0.396 7、0.183 0)。这主要是由于样地内采伐木以落叶松为主,原始林分落叶松树种比例较大,采伐后落叶松占比相对减少,增加了林分内树种组成结构的混交程度。说明在最优采伐方案时,随着采伐强度的增加,林分水平方向多样性有增加趋势。 开敞度与竞争指数受到采伐强度的影响最大。随着采伐株数强度的增加,开敞度得到大幅提升,且在采伐强度为40%的最优采伐方案时得到最大开敞度;随着采伐株数强度的增加,竞争指数也随之减小,在采伐强度为40%的最优采伐方案时,各样地竞争指数最小(1.866 8、1.905 1、2.239 4),表明林分内竞争状况得到改善。 林层比并未随强度增加而呈现出明显的递增变化趋势,表明林分内垂直多样性随采伐强度增大变化规律不明显。 总体看,各样地的最终优化函数Q值在采伐强度40%时筛选出的采伐方案取得最大值(42.001 3、42.370 5、23.346 5),达到了林分结构优化的目的。 表4 3块样地各抚育强度时结构指标及其变化幅度 由图2可见:以L01样地为例,模拟过程中最终筛选出各个采伐强度时的最优采伐木均集中于样地内树木分布密集的位置,表明各采伐强度梯度筛选出的最优采伐方案均从不同程度上释放了林木生长空间,并减弱林木间竞争压力的作用,从而达到调整林分空间结构的效果,与最初构建函数的目标一致。 由表5可见:天然落叶松林L01样地采伐前6 cm径阶林木偏少,但总体看,该林分径阶分布趋近于倒“J”型分布。对比各采伐强度时采伐木各径阶分布,趋势基本一致,这说明各采伐强度时最优方案对径级结构的调整波动较小。采伐木集中分布在6~12 cm径阶,在40%采伐强度时,最优方案共计采伐444株落叶松、107株白桦、1株樟子松。结合林分q值变化(见表4)与采伐前径级结构对比,采伐前6~12 cm径阶林木偏多,q值为1.569 8,在约束范围内稍高;而在40%采伐强度的最优采伐方案中,q值为1.485 0,q值降低,使得林分径级结构得到一定的改善。 ×为白桦;▲为采伐木;○为落叶松;△为云杉;□为樟子松。 采伐强度/%各径阶采伐木数量/株胸径6cm胸径8cm胸径10cm胸径12cm胸径14cm胸径16cm胸径18cm胸径20cm胸径22cm胸径24cm胸径26cm原样地238342251219143924628130310214309228196132774325110320184273202180110793622110230166234177157996135219024013720915113288522519902 原始林分直径分布q值基本分布在1.5~1.7之间,直径结构趋近于倒“J”型分布,林分内各单木竞争激烈;但林木大小分化程度则处于典型中庸状态,树种空间隔离程度较低,林分水平空间格局呈现随机分布状态,垂直结构分化与单木营养空间情况较为一般。 在设置的4个采伐强度梯度中,采伐株数强度为40%时,能够使得林分目标函数的平均值最大,分别为30.849 1、31.510 5、20.971 7,表明林分空间结构得到显著提升。 在40%株数采伐强度时,能够进一步筛选出最优采伐方案,使得林分目标函数达到最大值,分别为42.001 3(L01)、42.370 5(L02)、23.346 5(L03),优化幅度分别为59.01%(L01)、65.42%(L02)、108.47%(L03);此时,L01样地共计采伐580株、L02样地共计采伐228株、L03样地共计采伐148株。最优采伐方案使得林分内竞争状况、光照环境得到改善,树种混交程度增加,林分空间分布格局维持在随机分布状态,而林分垂直结构更趋于多样性,q值处于1.2~1.7范围内。 采用4种不同采伐模拟强度进行模拟时,林分整体目标值随着采伐强度的增大而增大,但各空间和非空间结构指标的变化情况不一致。随着采伐强度的继续增加,角尺度有一定降低趋势,大小比受到采伐强度的大小影响不大,而竞争指数则随采伐强度的增加而降低,混交度随着采伐强度的增加而增大。林层比受采伐强度影响相对较小,而单木营养空间则随着采伐强度的增大而增大。 本研究通过抚育采伐模拟实现对林分结构优化调整,采用随机抽样原则筛选出最优采伐木空间位置主要处于林木较为拥挤部分,且采伐后各目标值均有不同程度的改善。由于所考虑优化参数不止一个,但林分结构代表的是林分整体状态,因此全面考虑各个指标优化情况达到最佳状态才具备合理性。 本研究结果与张曼[27]、李婷婷等[28]研究结果相似,但与朱玉杰等[29]研究结果出现一定差异。其原因是本研究主要考虑的是抚育间伐强度对林分空间结构指标的影响,其受空间距离影响较大,当抚育间伐强度增加时能够使单木生长空间得到释放,林分内竞争环境大幅改良,改善林木分布格局,调节林内树种混交;但需要考虑的是,高强度的采伐将会导致林内生物量蓄积量的大幅降低,且此时,虽然林分内竞争指标及开敞度明显得到优化,但这2个指标的大小主要取决于最近相邻木距离的远近,并没有考虑冠层、林分多样性等方面的影响,同时采伐强度较大时,林分综合指标变化幅度增大,导致指标输出结果变得不稳定,因此,在确定采伐强度时,选取指标构建目标函数需要综合考虑多方面影响因素。 本文涉及到的采伐强度模拟主要考虑的是株数模拟强度,而采伐蓄积模拟强度的确定对森林经营同样具备较高实际意义,因此,如何控制蓄积模拟强度寻找最佳采伐木是一个重要问题。随着采伐强度的增加,模拟结果的变异系数逐渐增大,即结果的稳定性逐渐减小,模拟结果的变异程度和最优采伐强度之间的关系需要进一步研究。一些非空间结构指标,如生物量、蓄积量,本文并未做过多考虑,同时对林下植被的问题也并未涉及。下一步研究将采用物种更加丰富的天然林数据进行模拟及分析,为大兴安岭地区森林可持续经营提供参考。3 结果与分析
3.1 样地基本特征
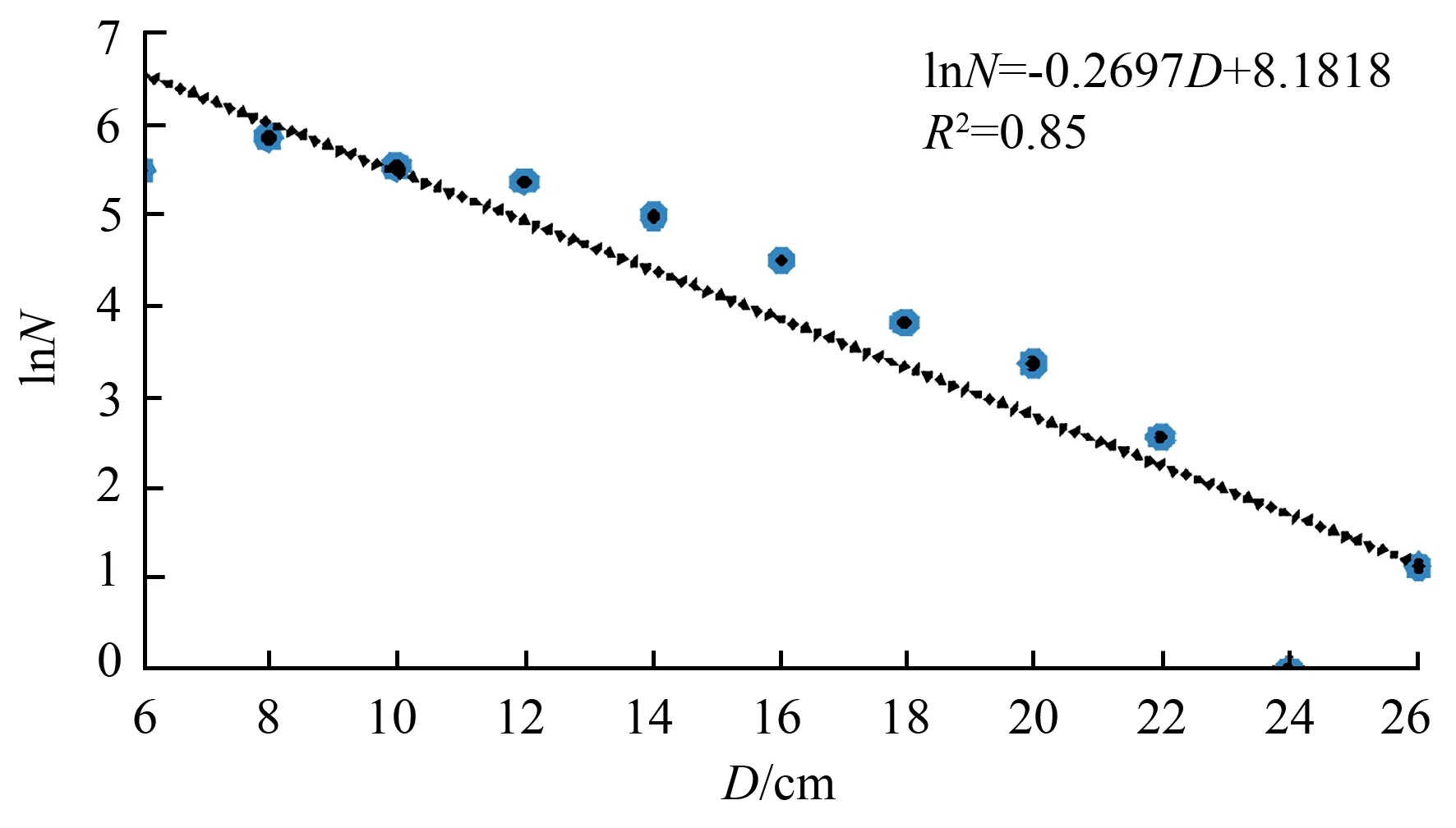

3.2 最优方案的分析与评价

4 结论
5 讨论
