大跨度三塔悬索桥弹塑性软钢阻尼器减震控制
2018-12-21张玉平邹仲钦陶天友郑文智
张玉平, 王 浩, 邹仲钦, 陶天友, 郑文智
(东南大学 混凝土及预应力混凝土结构教育部重点实验室,南京 210096)
大跨度悬索桥以其卓越的跨越能力受到桥梁工程界越来越多的重视,其结构类型从传统的独塔和双塔发展到了多塔悬索桥体系,常采用缆索支承体系,但该体系在强震作用下会因结构纵桥向刚度较小而引起过大的塔梁相对位移,从而引起支座严重损伤甚至破坏,进而引发主梁与引桥发生碰撞。因此,采取有效的减震措施以控制强震作用下结构关键部位的位移和内力,已成为大跨度悬索桥抗震领域的重点研究内容[1-2]。
国内外学者对传统的大跨度悬索桥的抗震性能[3]已经开展了不少研究。但大跨度三塔悬索桥作为一种新桥型,抗震性能的研究工作相对较少,其抗震性能备受关注。加之大跨度三塔悬索桥的跨度较大,其地震响应受行波效应的影响不可忽视[4-7]。例如,焦常科等研究认为,行波输入下大跨度三塔悬索桥地震响应具有一定的波动性;闫聚考等采用缩尺模型实验和有限元模拟对比的方法,发现大跨度三塔悬索桥中塔顶位移和北塔梁相对位移均明显增大,仅考虑一致激励不能保证大跨度多塔悬索桥的安全。
黏滞阻尼器与弹性拉索是用于大跨度桥梁减震控制的两种主要措施。如江阴长江大桥、美国金门大桥均采用黏滞阻尼器来控制主梁位移;泰州大桥在中塔与主梁间设置弹性拉索实现地震作用下塔梁相对位移的控制。焦常科等[8]分析了弹性拉索、黏滞阻尼器及二者组合使用对大跨度三塔悬索桥的减震控制效果,发现该类减震措施能够有效控制塔梁相对位移,但会显著增大中塔底内力响应。王浩等研究发现考虑行波效应时,在任意视波速下,黏滞阻尼器和弹性拉索对塔梁相对位移的控制效果较好,但中塔底剪力仍被显著放大。故采用新型阻尼器,开展大跨度三塔悬索桥的减震控制研究具有重要应用价值。
软钢是一种具有稳定滞回性能、较好的抗疲劳性能和温度变化低敏感性的金属材料[9-11],弹塑性软钢阻尼器由多片钢阻尼元件并联而成,该阻尼器利用软钢较强的塑性变形能力,通过钢板受力屈服来吸收和耗散能量,常安装在主梁和支撑点之间,在桥梁工程的减震控制中具有重要的潜在应用价值。国内众多学者对软钢阻尼器的相关形状参数及其力学性能进行了详细研究,并指出,灵活的截面设计使软钢阻尼器具有较大的使用空间和范围,可改善各种抗震等级下结构的抗震性能。软钢阻尼器在建筑结构抗震加固中得到了较多应用[12-13],在桥梁工程领域,南京夹江自锚式悬索桥已采用弹塑性软钢阻尼器作为减震措施,就目前而言应用效果良好[14]。国内外诸多学者针对软钢阻尼器对大跨桥梁抗震性能的改善已开展了一些研究工作[15-17]。如王浩等以江心洲大桥为例,研究了软钢阻尼器对独塔自锚式悬索桥减震控制效果,发现该桥的抗震性能有效提升。
大跨度三塔悬索桥作为一种新式桥型,其结构特性更趋复杂,强震作用下的地震响应控制面临更大挑战,为寻求更有效的减震措施以更好的控制其地震响应,本文尝试采用软钢阻尼器进行大跨三塔悬索桥减震控制研究,首先,对软钢阻尼器参数进行敏感性分析,获得最优控制参数,据此分别研究一致激励和行波激励下软钢阻尼器的减震效果,并重点分析视波速对减震效果的影响,以期探明软钢阻尼器是否能够更加有效地对大跨度三塔悬索桥的地震响应进行减震控制,从而为大跨度三塔悬索桥的减震设计提供可靠参考。
1 工程背景及有限元建模
本文以泰州大桥为工程背景,主桥布置为(390+1 080+1 080+390)m,如图1所示。主梁采用封闭式流线型扁平钢箱梁,梁宽39.1 m,中心线处梁高3.5 m;主缆矢跨比为1/9,主缆横向间距为35.8 m,采用预制平行钢丝索股;主塔为门式框架结构,两边塔为174 m高的混凝土结构,在横桥向均呈单柱形,中塔为倒Y形钢结构桥塔,高194 m。边跨与主跨主梁分离,在边塔下横梁处设置伸缩缝,主梁在中塔处呈漂浮状态,横向抗风支座设置在边、中塔与主梁之间,两边塔加劲梁处均布置竖向支座。

图1 泰州大桥结构布置图(m)
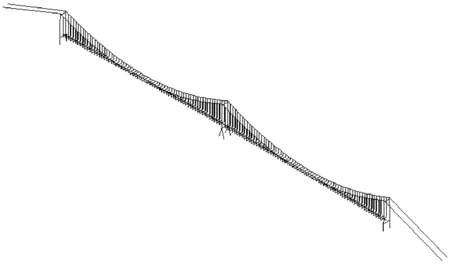
图2 三维有限元模型
图2为基于ANSYS建立的有限元模型,该模型采用空间梁单元Beam4模拟主梁与主塔,空间杆单元Link10模拟主缆与吊杆,并通过设置Link10的初应变同时采用应力刚化以考虑成桥状态下主缆与吊杆在重力荷载下的几何刚度[18]。主塔与主梁间纵桥向设置软钢阻尼器,采用Combin40单元模拟。主梁和吊杆间进行刚臂连接。
软钢阻尼器的恢复力模型可通过Ramberg-Osgood模型进行描述,并用于模拟软钢阻尼器刚度退化及其力-位移关系。在非线性分析中,为便于计算,该模型可简化为理想的双线性模型,如图3(a)所示。其中,Δy为屈服位移,Fy为屈服荷载,Δu为极限位移,Fu为极限荷载,K0为弹性刚度,K1为屈服后刚度;Combin40单元构造图,如图3(b)所示。用以模拟软钢阻尼器的力学性能,k1=K0-k2,k2=K1,FSLIDE=Fy,C为阻尼系数,GAP为间隙,本文中,C和GAP取为0。
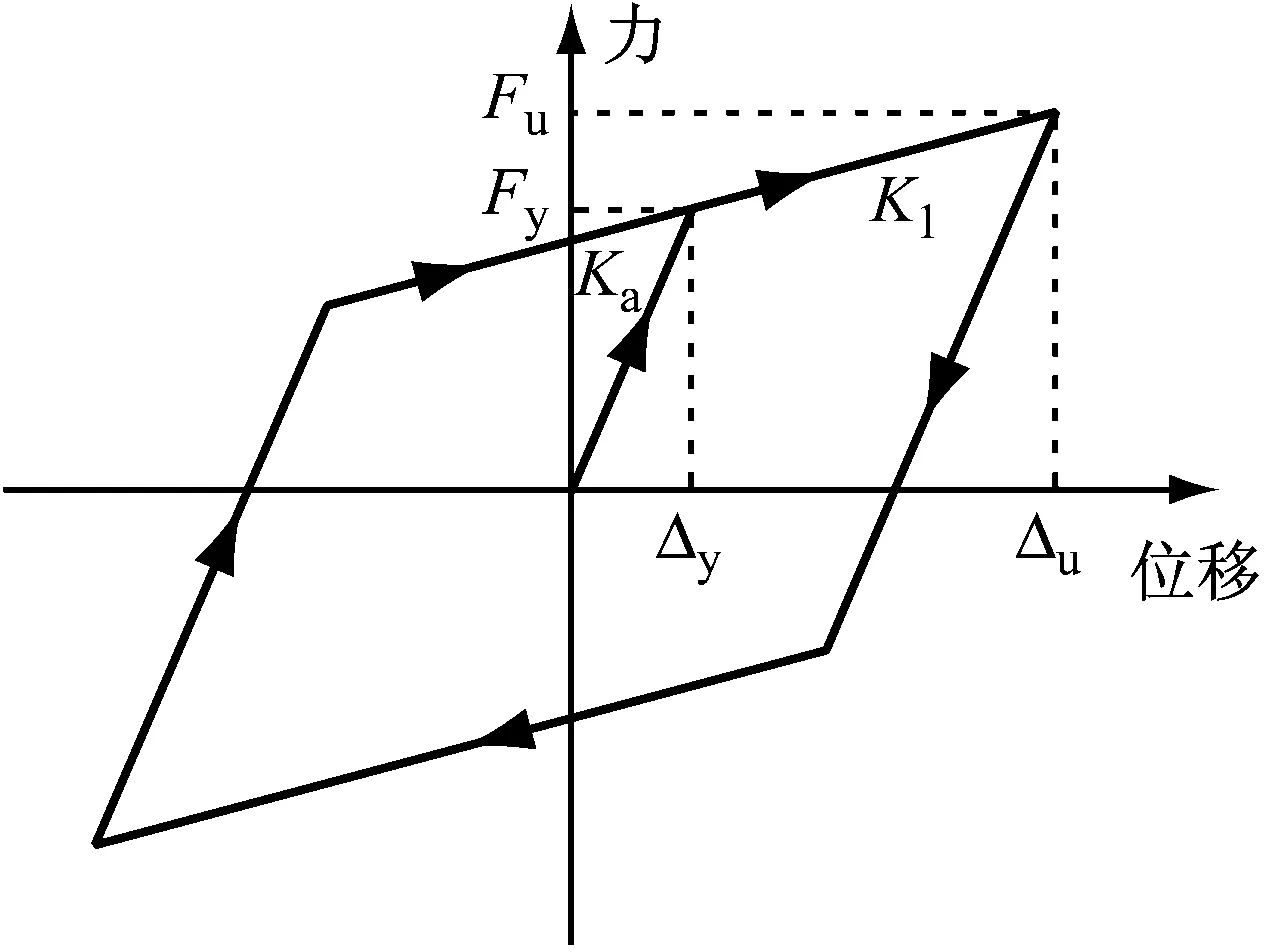
(a) 软钢阻尼器滞回模型
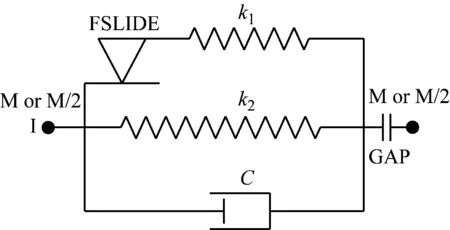
(b) Combin40单元
2 三塔悬索桥动力特性分析
本文采用子空间迭代法计算了结构前200阶模态频率与振型,涵盖了该三塔悬索桥的主要侧弯、竖弯和扭转振型,本文选取前26阶模态(见表1)进行分析。
由表1可知,该桥基频为0.071 63 Hz,属于长周期柔性结构,对应主梁1阶反对称侧弯振型;2阶频率为0.072 34 Hz,对应主梁反对称竖弯振型;1阶扭转振型出现在第14阶模态,为主梁1阶反对称扭转加主塔扭转,对应频率为0.272 90 Hz。可见,该三塔悬索桥的动力特性与传统大跨度的两塔悬索桥相比,存在很多相似之处,也有明显的差异。
3 软钢阻尼器的参数敏感性分析
3.1 屈服荷载
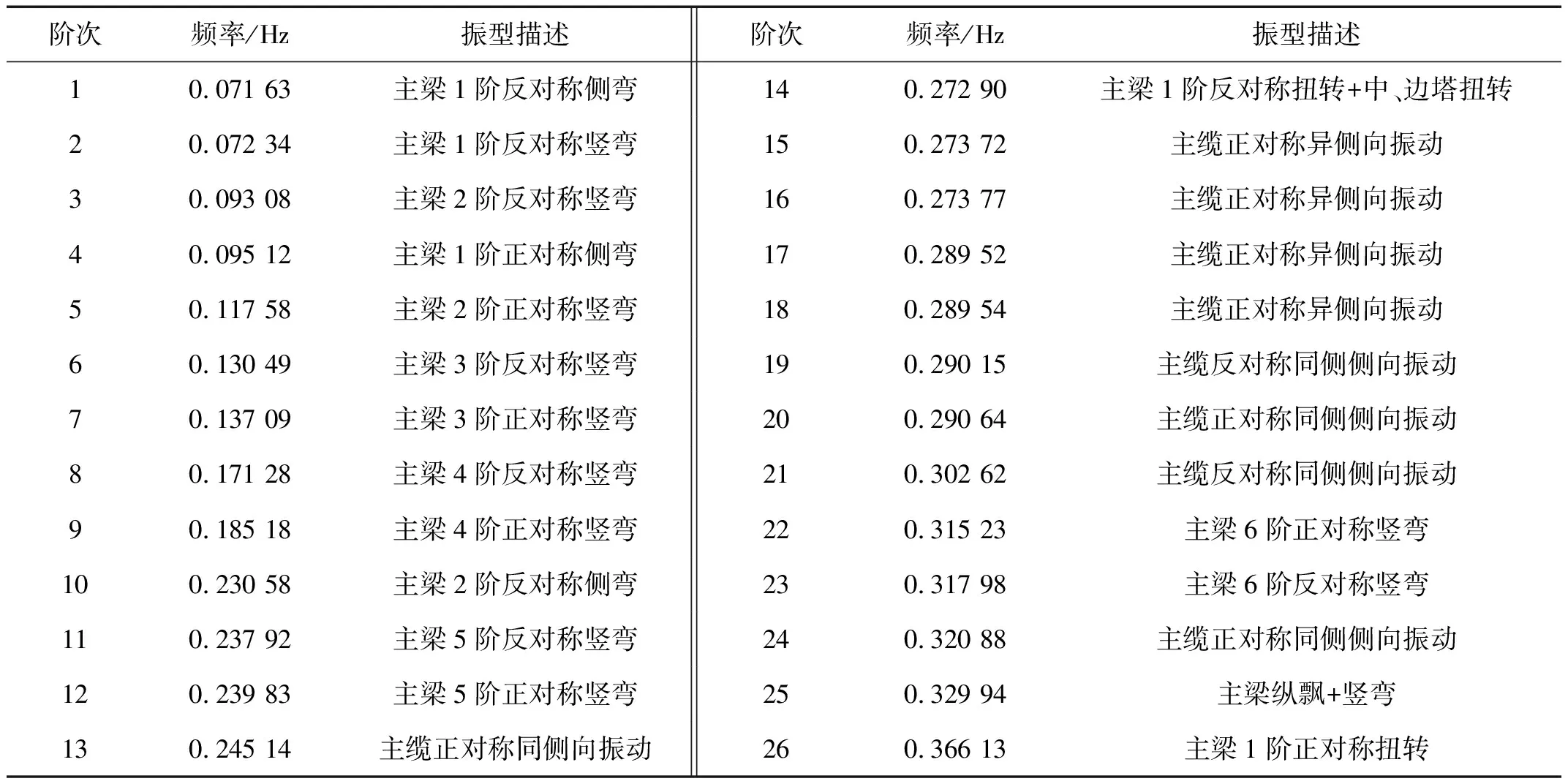
表1 前26阶模态
本文参照南京过江通道右汊夹江大桥E型软钢阻尼器的参数展开研究,在泰州大桥的塔梁连接处均设置相同参数的软钢阻尼器,阻尼器的屈服位移Δy为10 mm,极限位移Δu为屈服位移的15倍,极限荷载Fu为屈服荷载Fu的1.15倍,屈服荷载初设为6×106N。由于缺乏该桥桥址区拟合人工地震波,现选取El Centro、Taft和Tianjin三条地震波进行了初步分析,分析过程中地震波峰值根据该桥桥址区地震危险性分析结果(见表2)进行了调整。本文后续分析中取三条地震波中响应最大的Tianjin波进行地震波输入,暂未考虑行波效应。
当屈服荷载为6×106N时,所有桥塔处软钢阻尼器的最大位移均超过极限位移,表明软钢阻尼器已失效。为此,本文假设软钢阻尼器的屈服位移保持不变,通过提高其屈服荷载增强软钢阻尼器的耗能能力,使得软钢阻尼器的位移满足要求。在此基础上,进一步对软钢阻尼器屈服荷载进行参数敏感性分析。不同屈服荷载条件下结构典型位置的地震响应峰值,如表3所示。
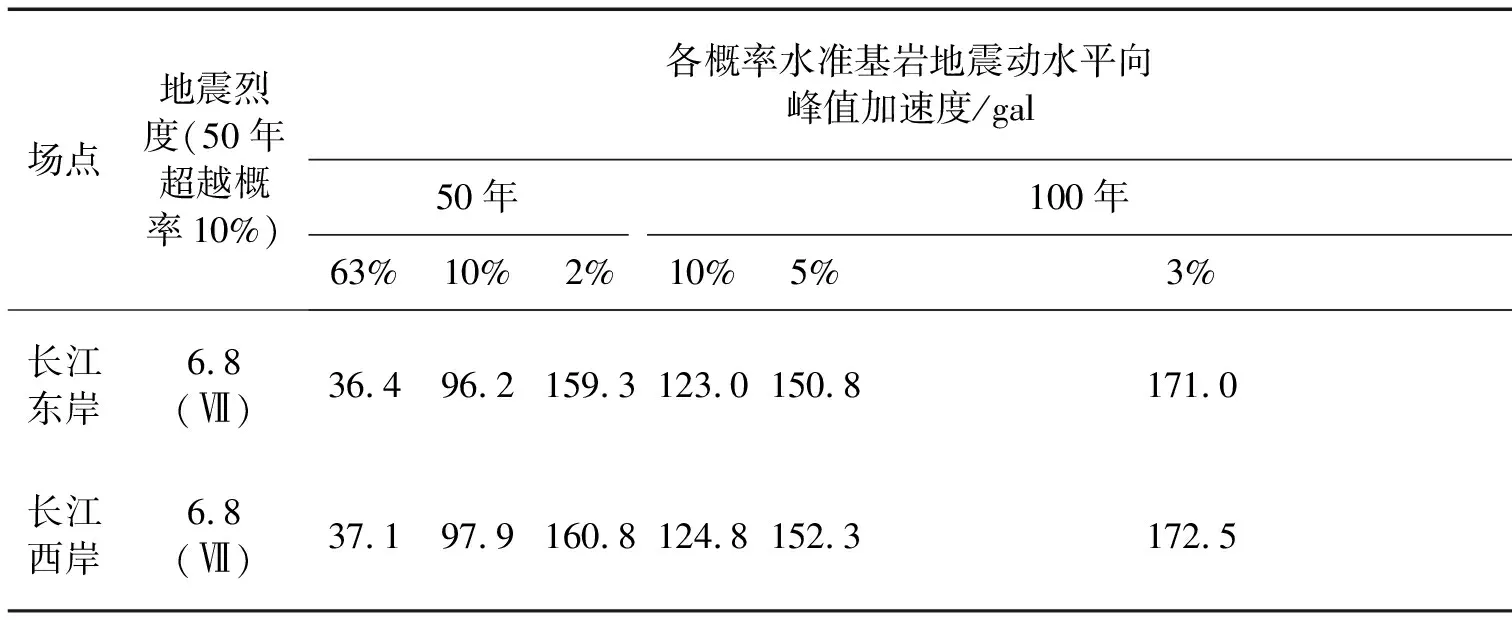
表2 桥址区地震危险性分析结果
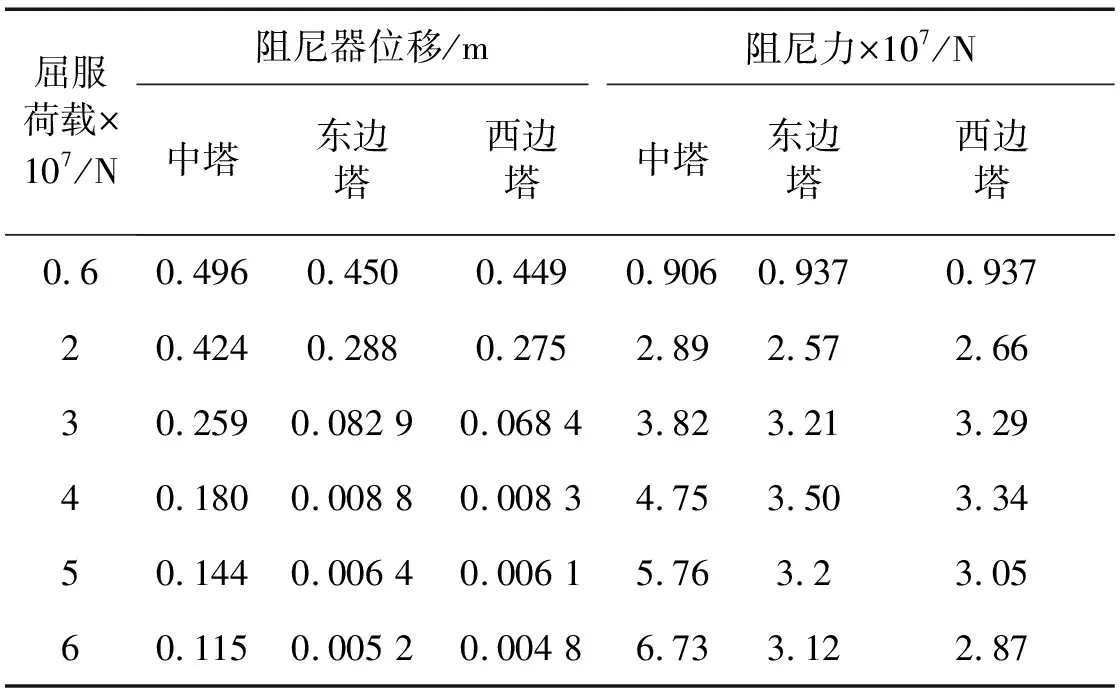
表3 Tianjin波输入下软钢阻尼器的响应峰值
由表3可知,Tianjin波输入下,屈服荷载大于0.6×107N时,随着屈服荷载的增大,软钢阻尼器的耗能能力得以提升,阻尼器的阻尼力不断增大而阻尼器的位移不断减小。当屈服荷载达到5×107N时,阻尼器位移峰值小于极限位移,此时为满足位移使用要求的最小值,因此,后续分析中屈服荷载取为5×107N。
3.2 弹性刚度
屈服位移是体现软钢阻尼器屈服性能的另一个重要参数。当屈服荷载确定时,屈服位移和弹性刚度成反比。为此,基于上述屈服荷载,进一步分析软钢阻尼器减震效果对弹性刚度的参数敏感性。软钢阻尼器弹性刚度的变化区间取为1×108~3×109N/m。结构关键部位地震响应峰值,如图4所示。
由图4可知:①当弹性刚度大于1×108N/m时,塔梁相对位移迅速减小,软钢阻尼器控制效果较为明显;当大于1×109N/m时,塔梁相对位移趋于稳定;②软钢阻尼器会使得塔顶位移、塔底剪力和塔底弯矩等均有所增大,在进行抗震设计时应予以关注,并且当弹性刚度大于1×109N/m时,各内力峰值趋于稳定,此时,软钢阻尼器弹性刚度的增加对内力峰值影响可忽略;③综合考虑塔梁相对位移、塔底内力和塔顶位移等因素,软钢阻尼器弹性刚度选为1×109N/m。
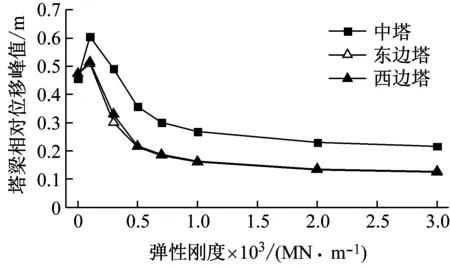
(a) 塔梁相对位移
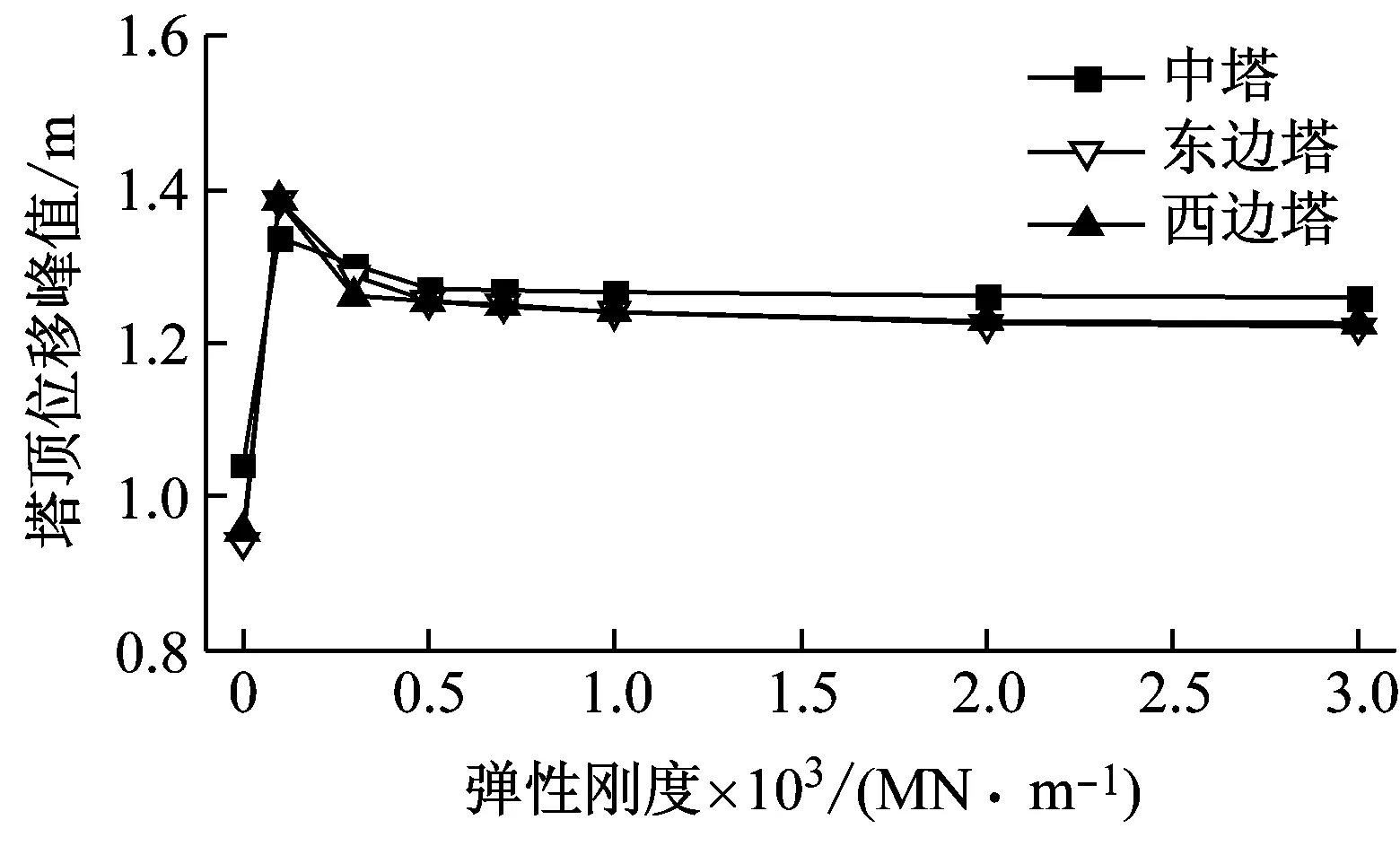
(b) 塔顶位移
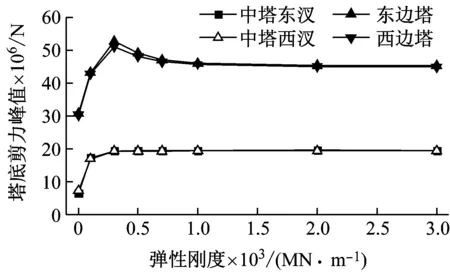
(c) 塔底剪力
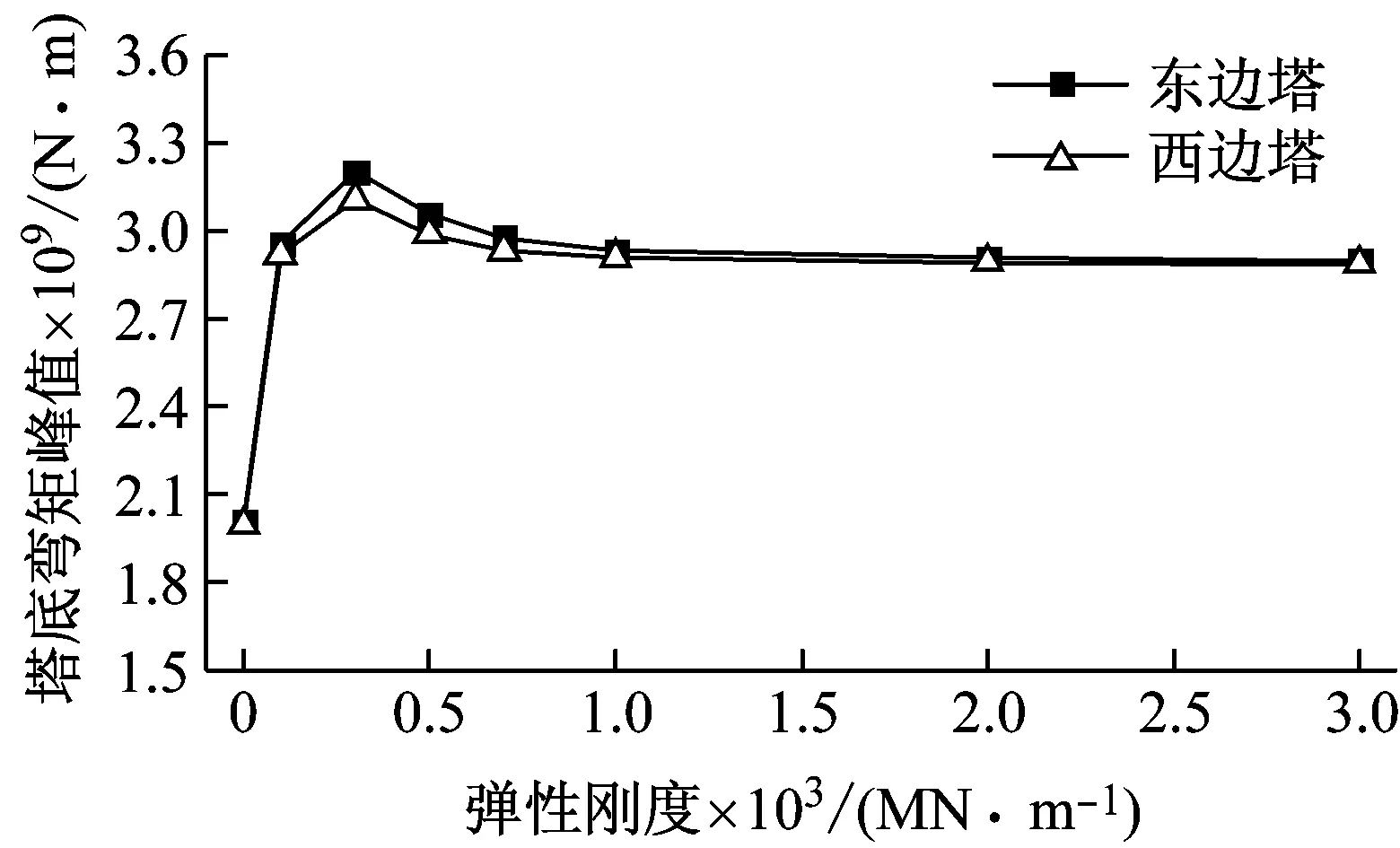
(d) 塔底弯矩
Fig.4 Relationships between the seismic peak responses on key parts and elastic stiffness(Tianjin)
4 大跨度三塔悬索桥软钢阻尼器的减震分析
4.1 一致激励下的软钢阻尼器减震分析
基于软钢阻尼器参数敏感性分析的结果,选取屈服荷载5×107N,弹性刚度1×109N/m开展大跨度三塔悬索桥软钢阻尼器的减震控制效果研究。首先,在一致激励下对比了设置软钢阻尼器前后各桥塔的位移与内力响应峰值,结果如表4所示(表中的响应峰值均减去了初始响应值,下同)。考虑到结构的对称性,本文地震响应仅以东边塔和东边缆为例。
表4结构关键部位地震响应峰值及减震率
Tab.4Seismicpeakresponsesandthevibrationdecreasingratiosofkeypartsofthestructure
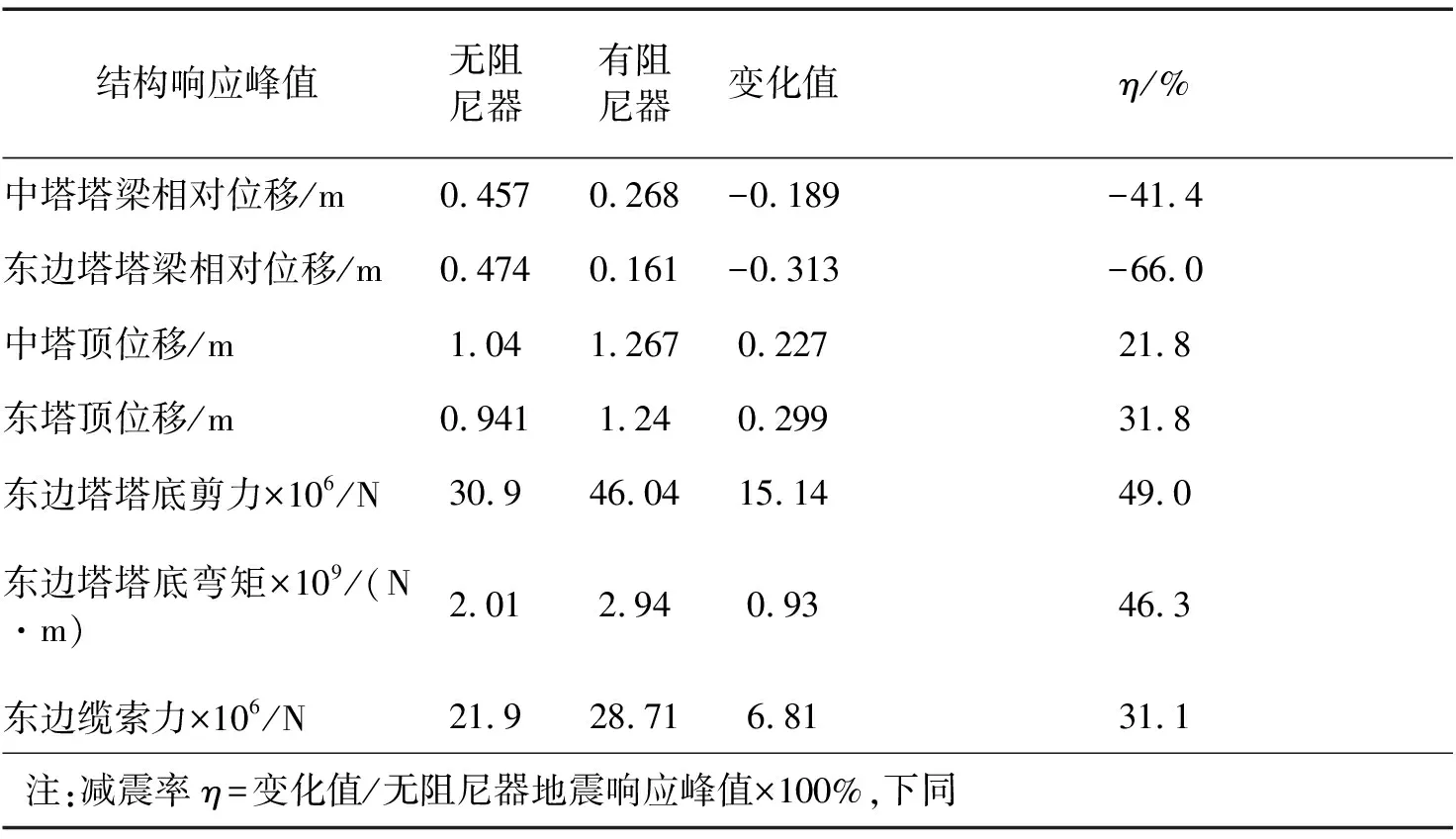
结构响应峰值无阻尼器有阻尼器变化值η/%中塔塔梁相对位移/m0.4570.268-0.189-41.4东边塔塔梁相对位移/m0.4740.161-0.313-66.0中塔顶位移/m1.041.2670.22721.8东塔顶位移/m0.9411.240.29931.8东边塔塔底剪力×106/N30.946.0415.1449.0东边塔塔底弯矩×109/(N·m)2.012.940.9346.3东边缆索力×106/N21.928.716.8131.1注:减震率η=变化值/无阻尼器地震响应峰值×100%,下同
由表4可知,在设置软钢阻尼器后,塔梁相对位移均显著减小,相较于中塔,边塔减震效果更佳,变化值增大0.124 m。然而,软钢阻尼器的设置会使主塔塔顶位移有一定程度的增大,并对边塔的影响相对较大,同时,还引起了结构内力的重分配,使得塔底剪力与弯矩发生显著变化。其中,边塔塔底剪力与弯矩变化最大,增长幅值接近50%;边缆索力相对变化较小,仅为31.1%。因此,采用软钢阻尼器作为减震控制措施时,在考虑塔梁相对位移减震效果的前提下,需考虑软钢阻尼器的设置对主塔内力的不利影响。
4.2 考虑行波效应时软钢阻尼器减震分析
为研究行波效应的影响,进一步重点分析了不同视波速下软钢阻尼器的减震效果。地震波沿纵桥向输入,传播方向假定为从东到西,输入点包括东锚碇、东边塔塔底、中塔塔底、西边塔塔底和西锚碇。为便于和一致激励下的结果进行对比,软钢阻尼器的参数取值与一致激励下保持一致,且视波速最大取值为8 000 m/s来验证行波分析的可靠性。图5为不同视波速下三塔悬索桥的地震位移响应峰值,并提取了典型视波速下的地震响应位移时程,结果见图6。
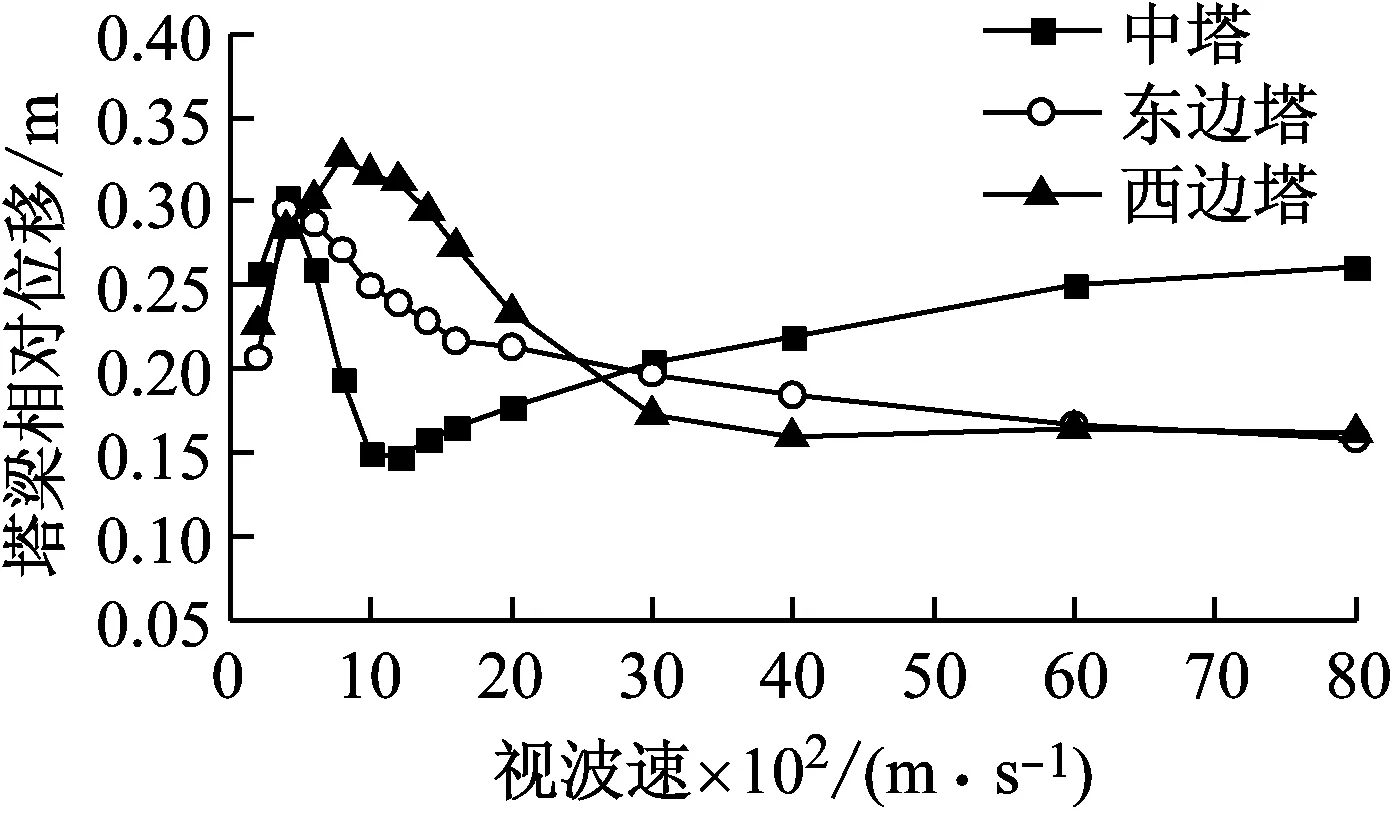
(a) 塔梁相对位移峰值
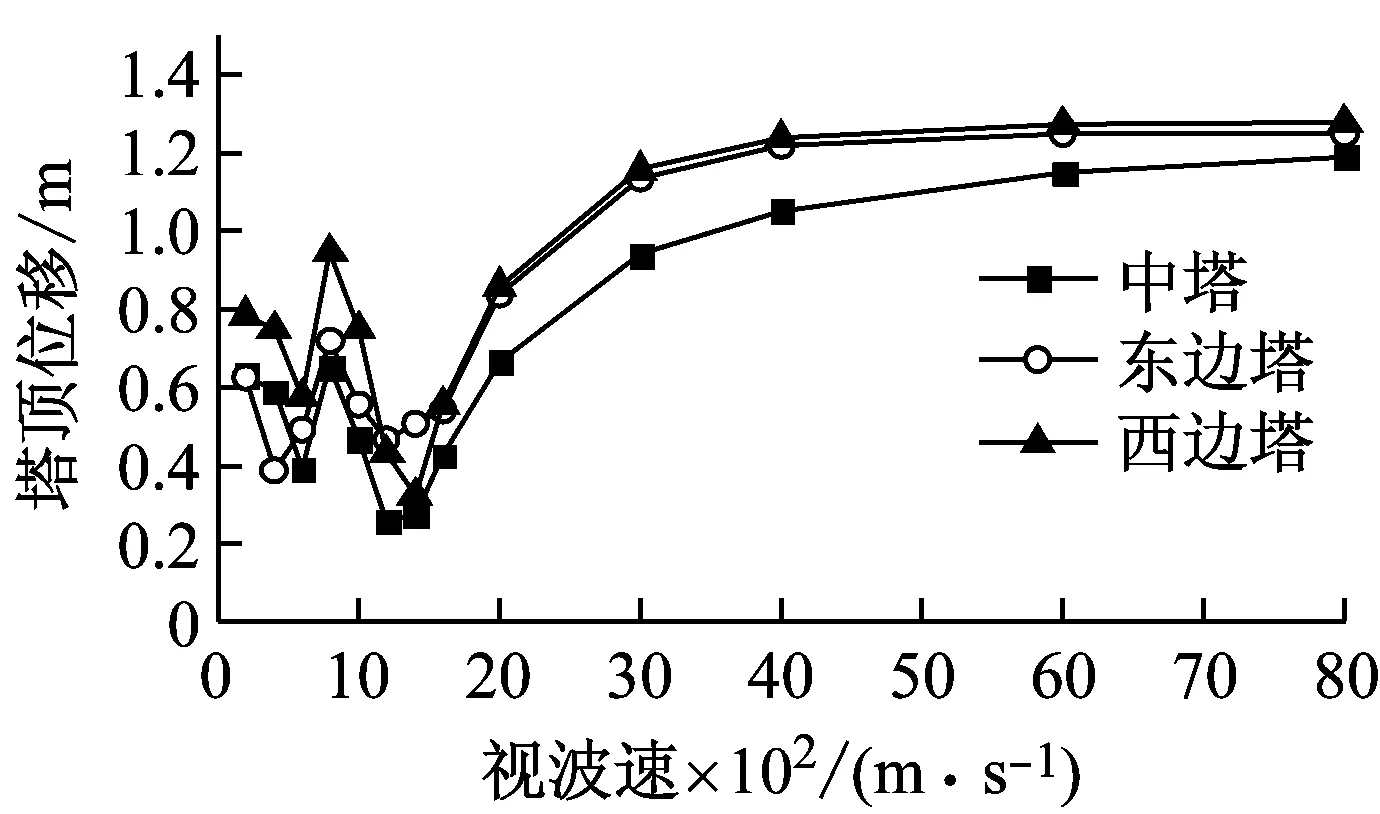
(b) 塔顶位移峰值
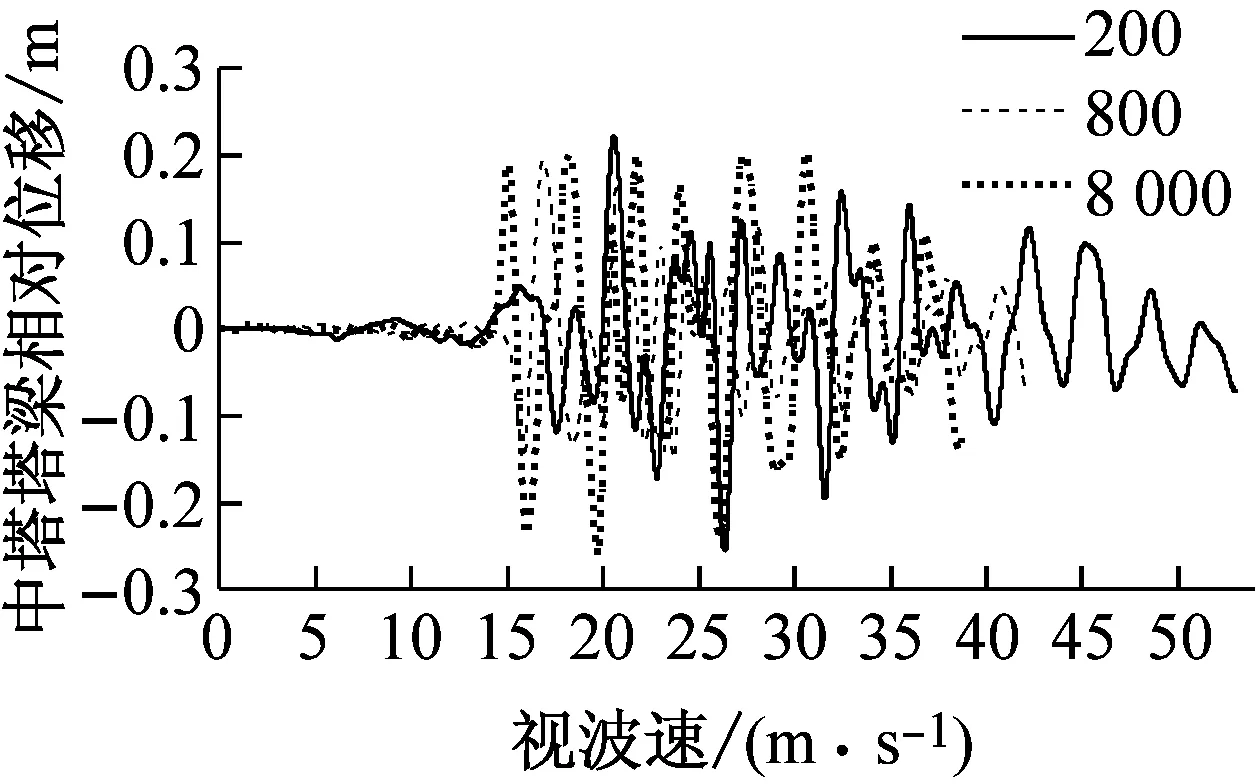
(a) 中塔塔梁相对位移时程
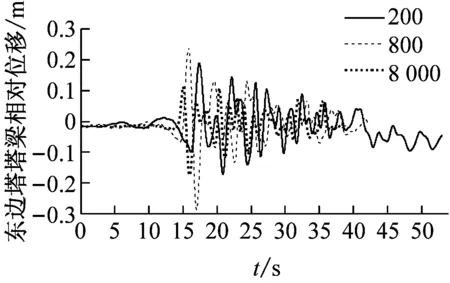
(b) 东边塔塔梁相对位移时程
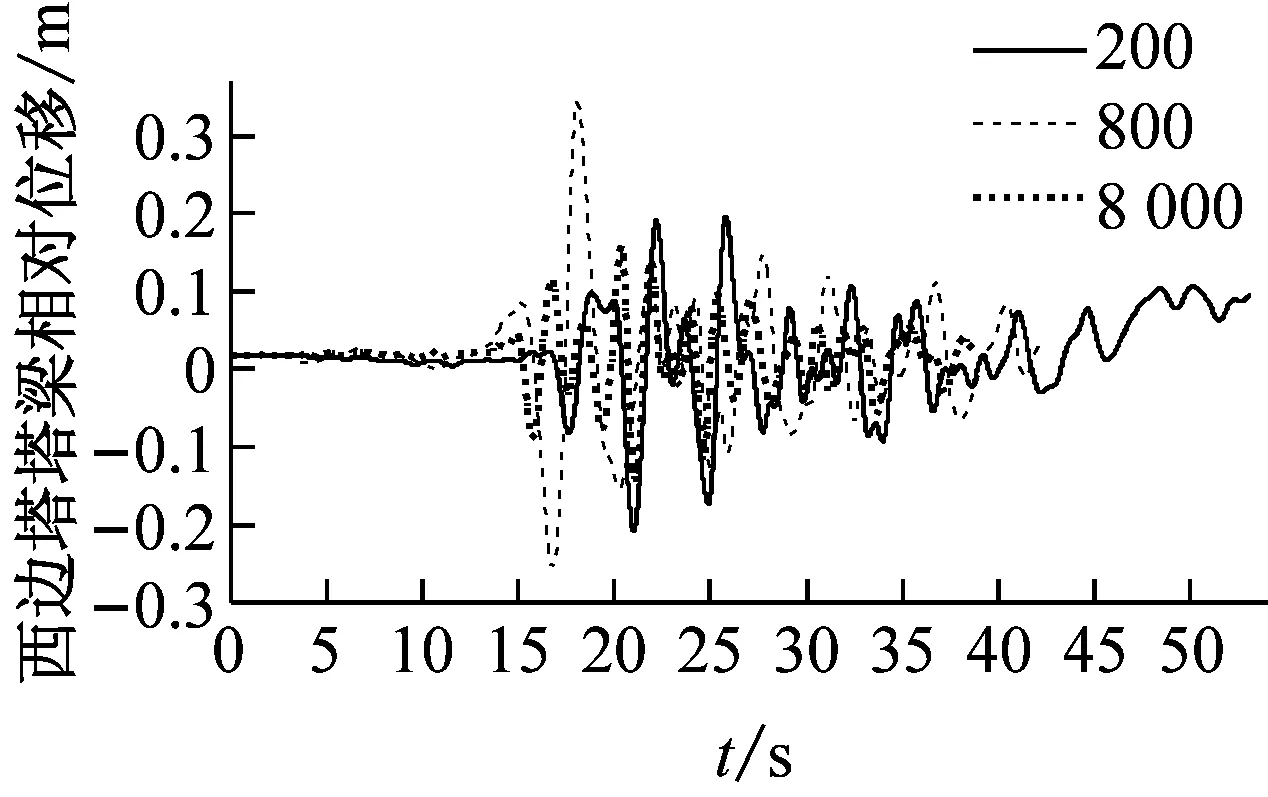
(c) 西边塔塔梁相对位移时程
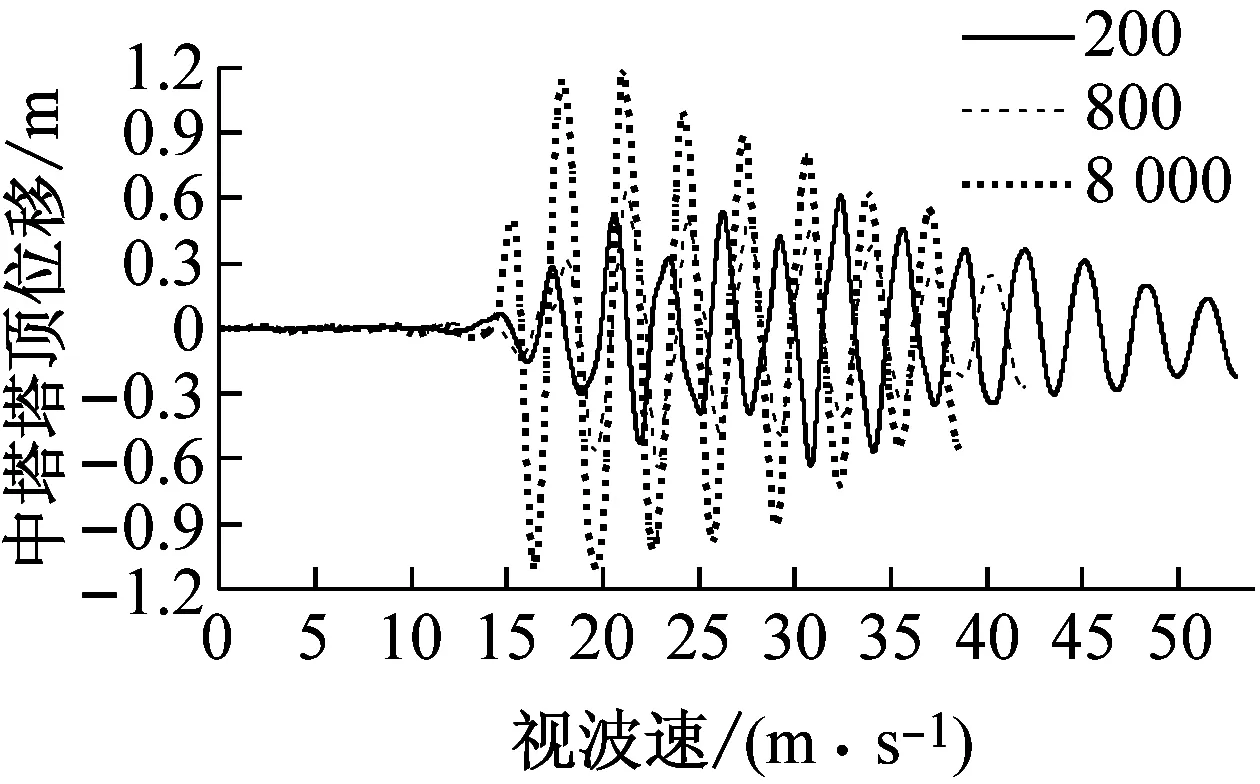
(d) 中塔塔顶位移时程
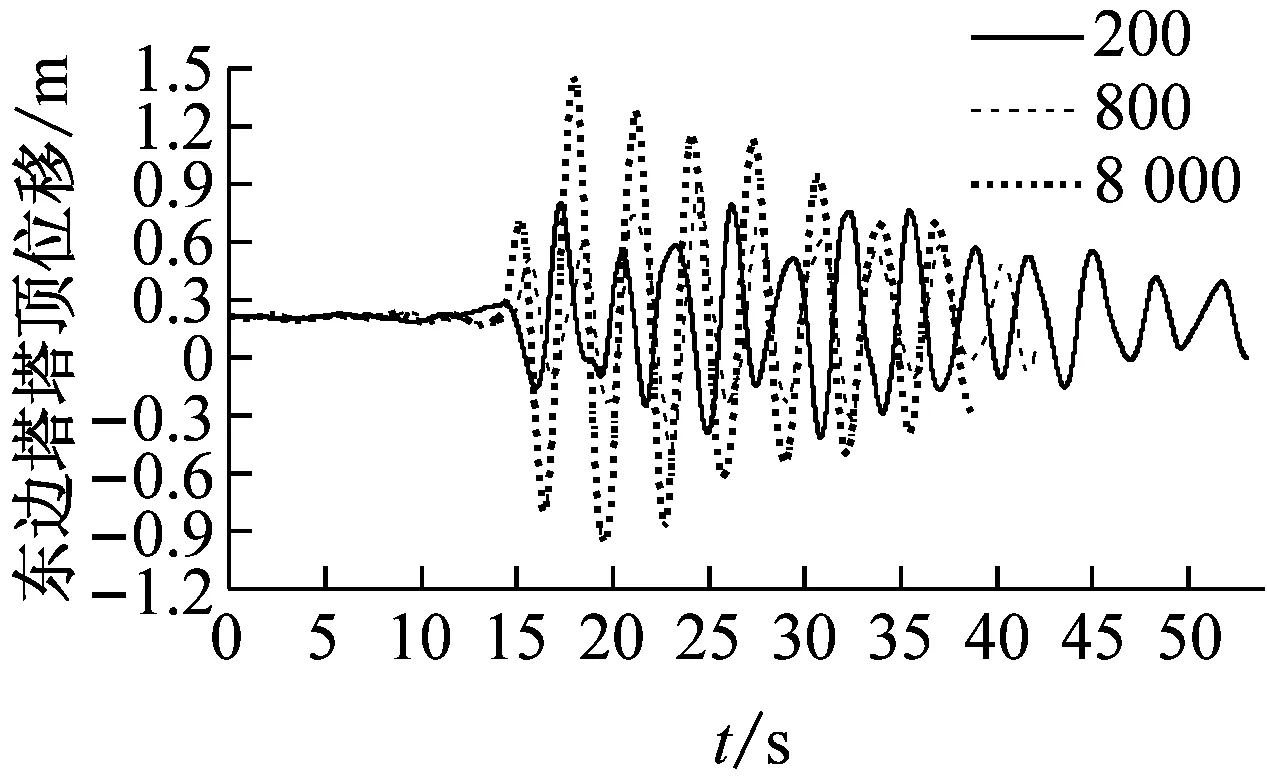
(e) 东边塔塔顶位移时程
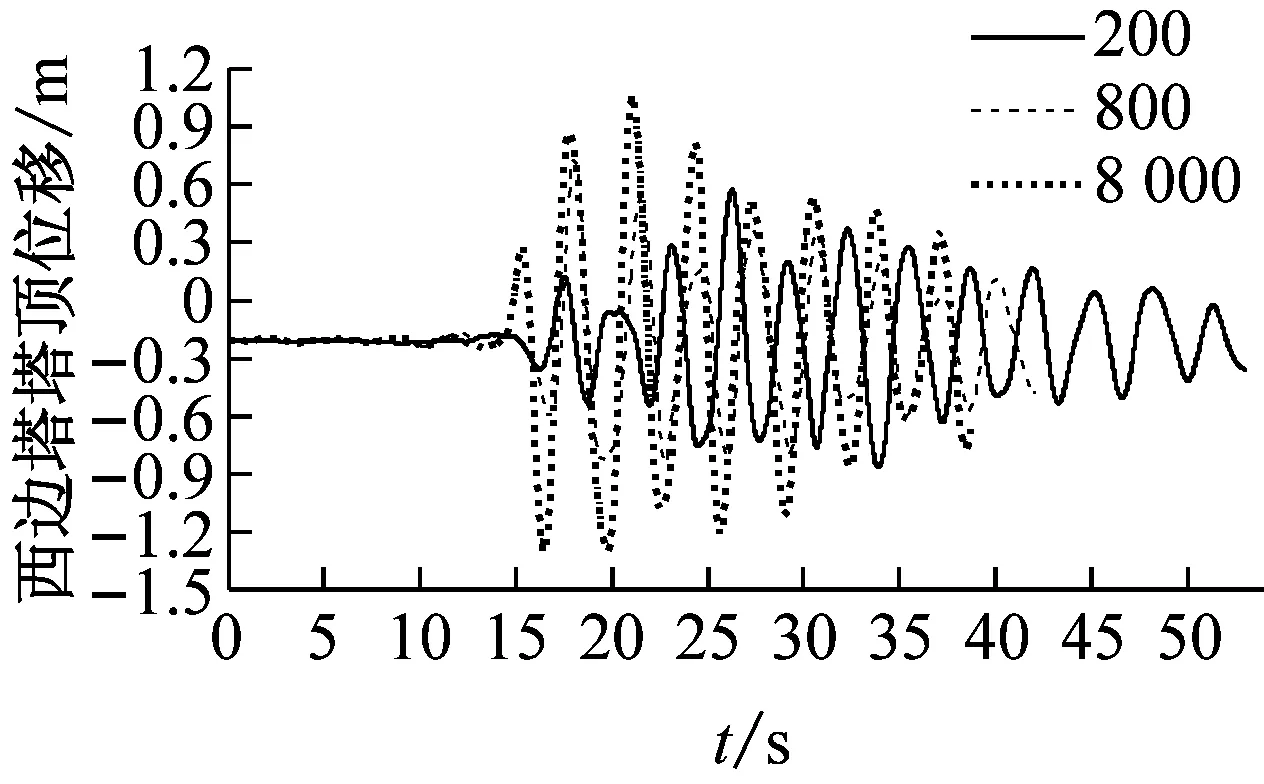
(f) 西边塔塔顶位移时程
由图5和图6可知:①设置软钢阻尼器后,随着视波速的增大,塔梁相对位移总体上先增后减,且大于6 000 m/s时趋于稳定;两边塔幅值差异明显,且低视波速下峰值均远大于稳定值,而中塔在大于1 000 m/s时又逐渐增加而后趋于稳定。由此可见,仅考虑一致激励下的位移响应为控制目标进行抗震设计是不合理的。②各主塔塔顶位移在低视波速区间振荡而后逐渐增加,并在大于3 000 m/s后趋于稳定。③综合来看,低视波速下,大跨度三塔悬索桥塔梁相对位移所受影响较为显著,这主要与结构本身、地震波特性、视波速有关;大于3 000 m/s时,均接近一致激励下的结构位移响应。
图7和图8表明:①视波速在400~1 200 m/s时,各塔底剪力随视波速的增加先增后减;大于1 200 m/s时,各塔塔底剪力随着视波速的增加而增加,并在大于3 000 m/s后趋于稳定;②与主塔塔顶位移响应类似,边塔塔底弯矩和边缆索力均表现为低视波速区间振荡,且不同步,高视波速区间趋于平稳;当大于3 000 m/s时,接近一致激励下的结构内力;③总体而言,近震源端塔底内力与远震源端在低视波速下有所差别,但在高视波速下趋于一致激励。
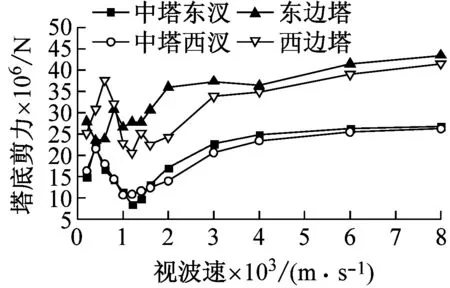
(a) 塔底剪力峰值
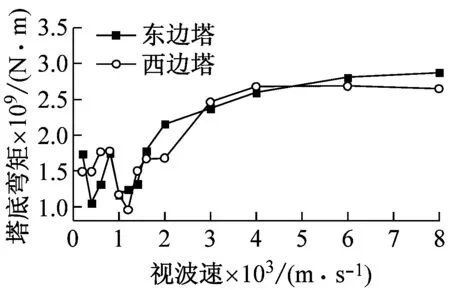
(b) 塔底弯矩峰值
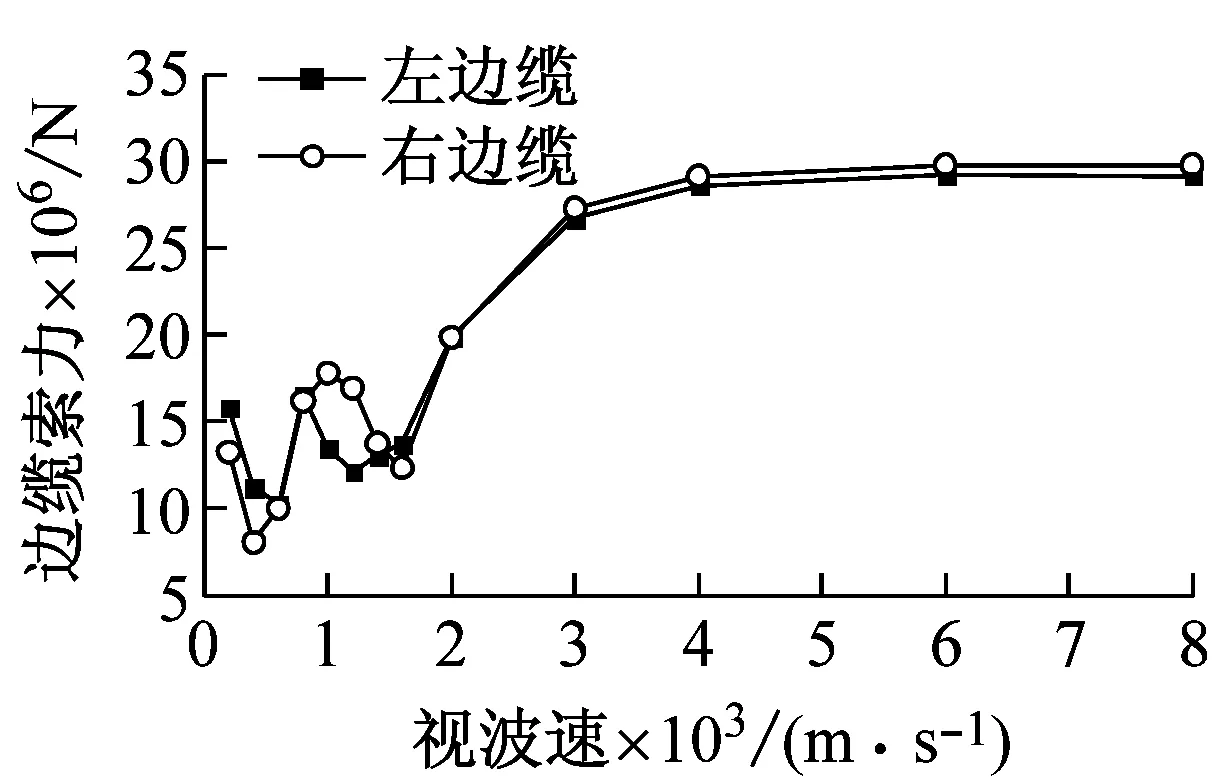
(c) 边缆索力峰值
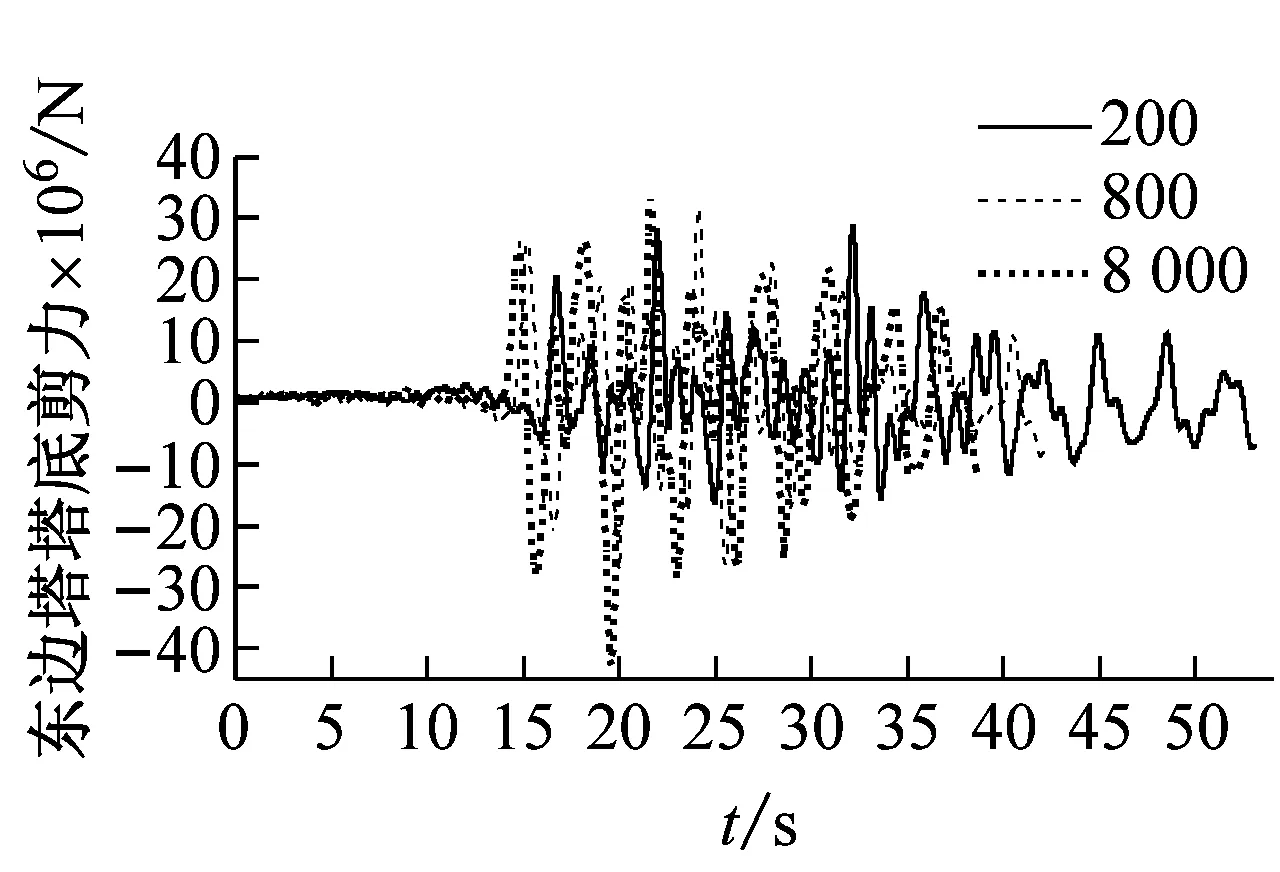
(a) 东边塔塔底剪力时程
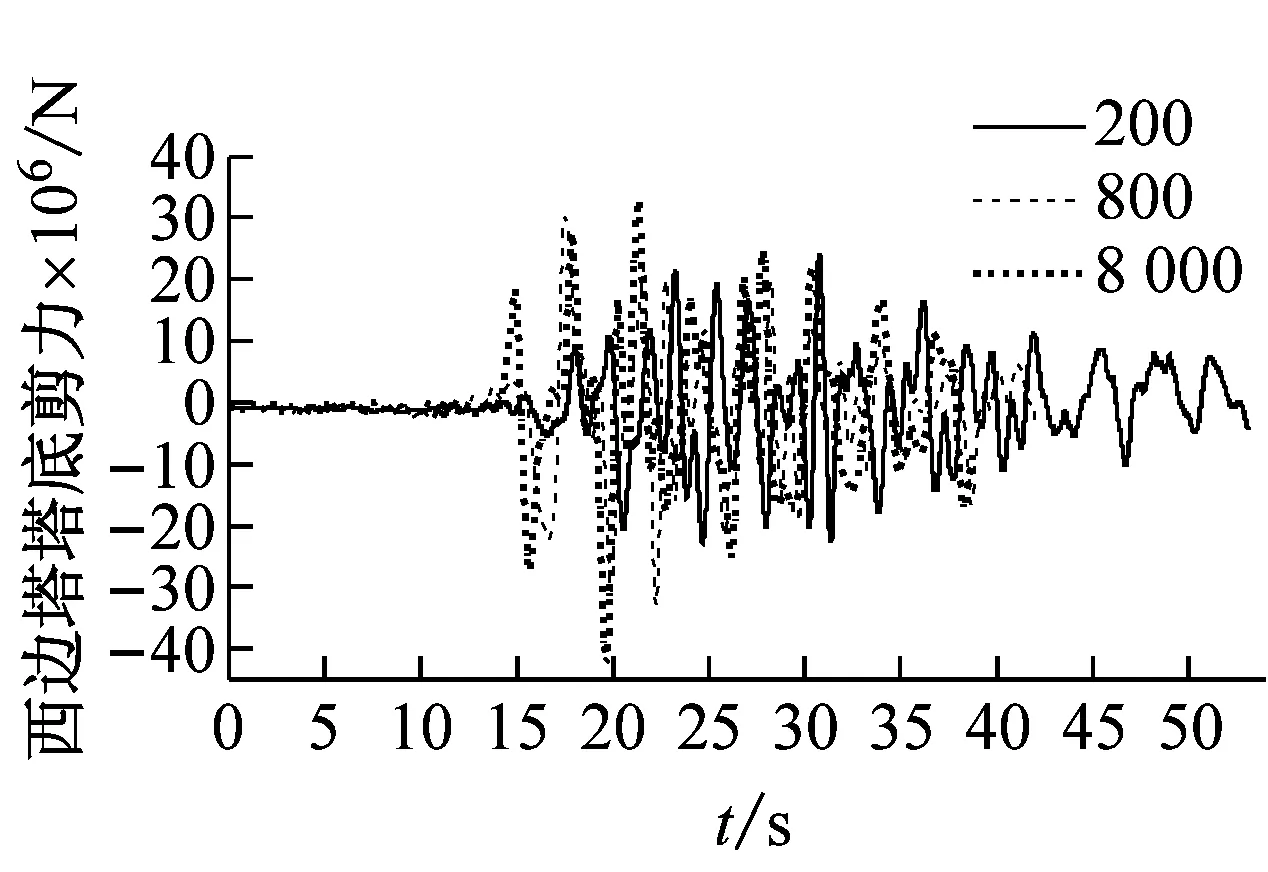
(b) 西边塔塔底剪力时程
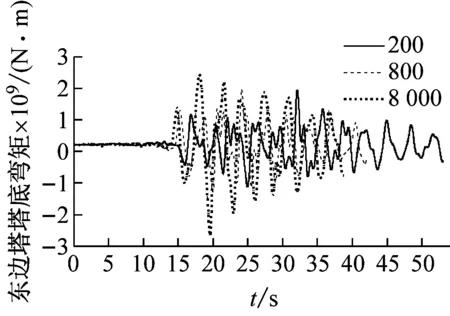
(c) 东边塔塔底弯矩时程
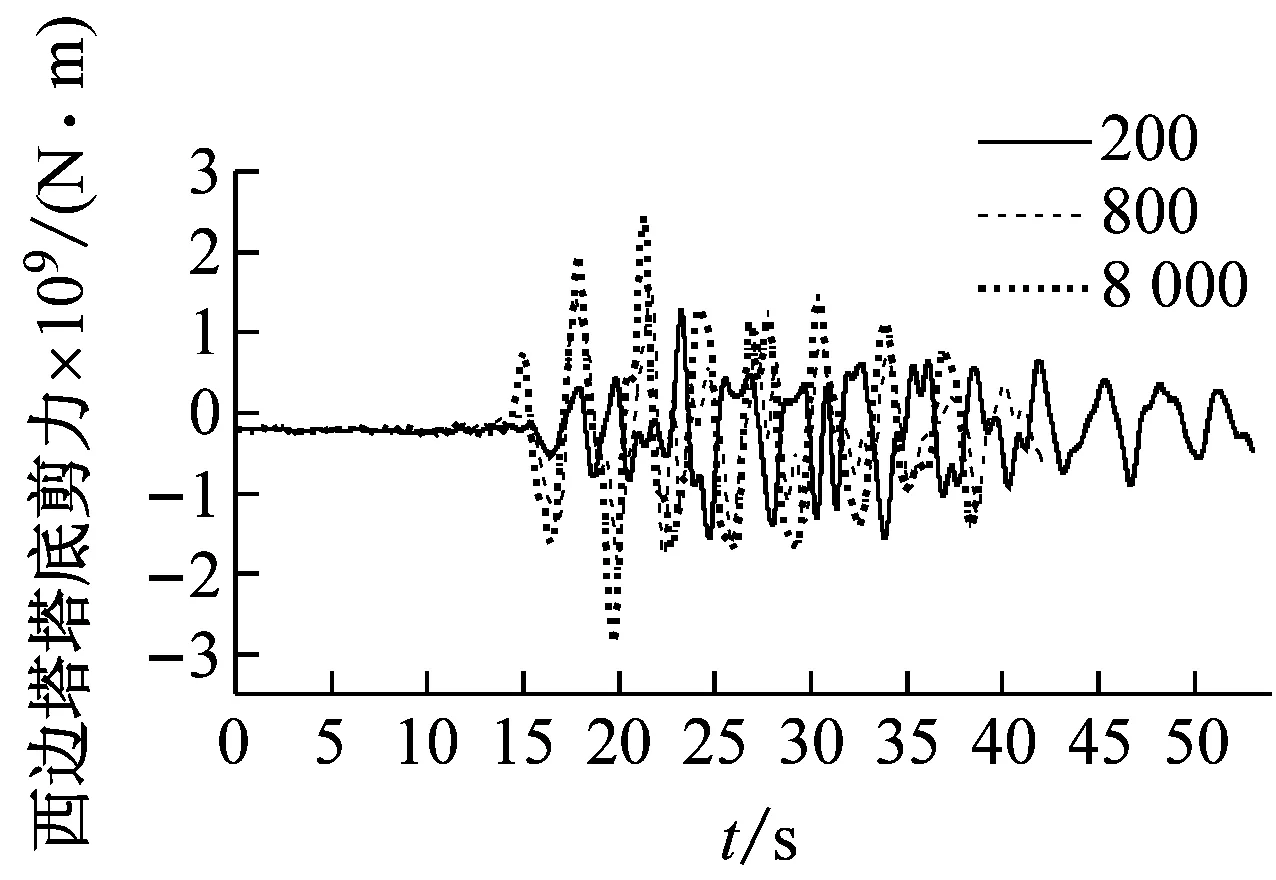
(d) 西边塔塔底弯矩时程
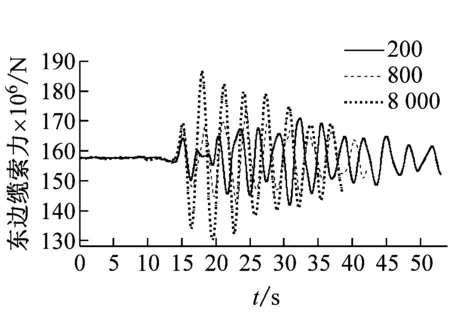
(e) 东边缆索力时程
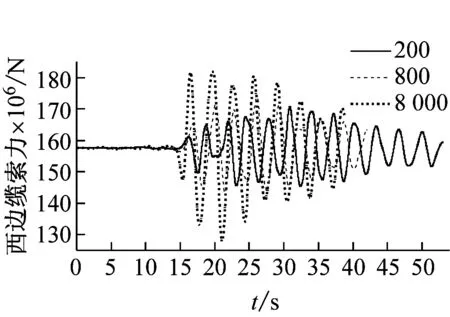
(f) 西边缆索力时程
4.3 结果分析
在不同视波速下,软钢阻尼器对结构典型部位地震响应的减震效果见表5。
由表5可知:在不同视波速下,软钢阻尼器对大跨度三塔悬索桥塔梁相对位移的控制效果均较好。对中塔的减震率大都维持在-40%以上,且在1 400 m/s时,达到最值-63.7%;对东边塔的减震率随着视波速的增大而缓慢增大,在-29.8%~-66%范围内变化;当视波速大于800 m/s时,对西边塔的减震率持续稳定上升,并在高视波速下维持在-70%以上。
然而,阻尼器的设置会使中塔塔底剪力显著增大,减震率最大至300%。阻尼器对边塔内力控制效果呈波动趋势,且东西两边塔有一定差别。具体表现为,视波速小于1 200 m/s时,软钢阻尼器对东边塔底剪力、弯矩起减震作用,减震率最大分别可达-21.3%、-34.3%,而远震源端西边塔存在波动;随着视波速继续增大,软钢阻尼器的设置会使近震源端东边塔的内力增大,而对远震源端西边塔的塔底剪力和弯矩减震效果良好,并且在视波速1 200~2 000 m/s范围内,达到相对较优;在视波速大于3 000 m/s时,软钢阻尼器使两边塔塔底内力不断增大并趋于一致激励。
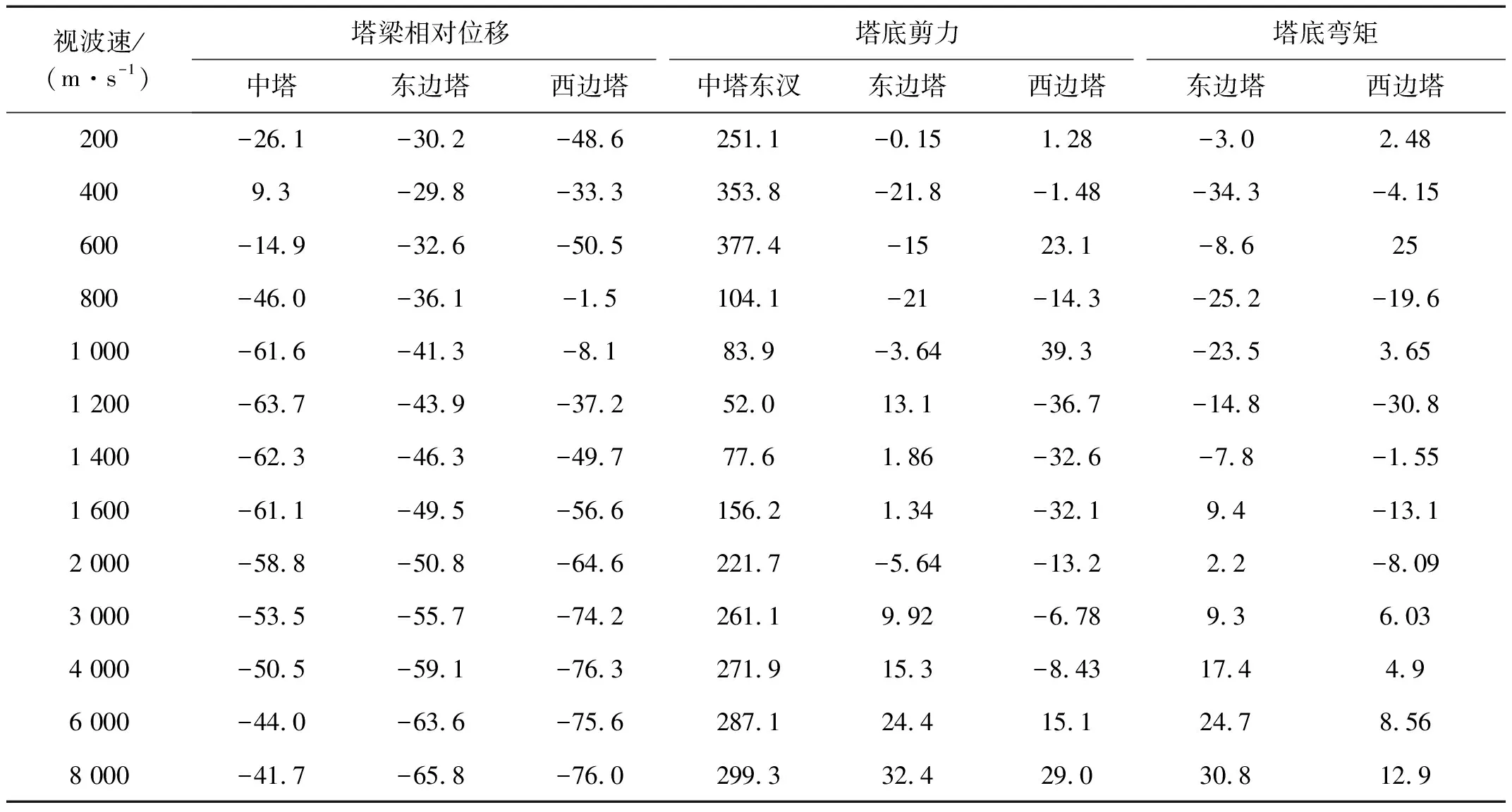
表5 行波激励下结构关键部位地震响应的减震率η
由以上分析可知,不同视波速下,软钢阻尼器的减震效果差异较大。由于视波速的不同,地震波对结构不同部位的激励存在着相位差,致使结构内力在地震作用下的波动明显,软钢阻尼器的减震效果不一,在视波速低于1 200 m/s时,软钢阻尼器对近震源的主塔内力地震响应的控制效果较好,而视波速高于1 200 m/s后远震源端地震响应控制效果明显提高并超越近震源端,同时,软钢阻尼器的设置仍会使中塔底剪力有所增大。总体而言,在行波激励下,相较于弹性拉索和黏滞阻尼器,软钢阻尼器对塔梁相对位移的减震效果最佳;三种减震装置均会使中塔塔底剪力明显增大,且弹性拉索增幅最大,其次为软钢阻尼器,黏滞阻尼器增幅最小。由此可见,软钢阻尼器可在不显著增大中塔塔底内力的前提下,有效控制塔梁相对位移。
5 结 论
本文以泰州大桥为研究背景,开展基于软钢阻尼器的大跨度三塔悬索桥减震控制研究,所得结论主要包括:
(1) 一致激励和行波激励下,软钢阻尼器可显著减小塔梁相对位移,减震率大多能达30%以上,但阻尼器的设置会增大塔顶位移、塔底剪力和弯矩,其中塔底剪力相对较为明显,应予以重点关注。
(2) 行波激励下,大跨度三塔悬索桥内力表现出明显的振荡特征,软钢阻尼器减震效果受低视波速的影响显著;当视波速大于3 000 m/s时,塔底内力逐渐稳定并接近于一致激励,减震效果受视波速的影响逐渐减小;在800~2 000 m/s时范围内,软钢阻尼器减震效果相对较优。
(3) 不同视波速下,软钢阻尼器对两边塔地震响应减震效果差异明显。在视波速低于1 200 m/s时,软钢阻尼器对近震源端结构地震响应控制效果优于远震源端;视波速高于1 200 m/s后远震源端明显提高并超越近震源端。
(4) 相较于黏滞阻尼器和弹性拉素,软钢阻尼器可在不显著增大塔底内力的前提下,实现塔梁相对位移的有效控制,其减震效果明显更优。
值得说明的是,本文仅针对泰州大桥这一特定大跨度三塔悬索桥进行了分析,故研究结论的通用性尚需在其他类型大跨度三塔悬索桥中进一步验证,以期为大跨度三塔悬索桥的减震分析与设计提供参考。
