基于包络谱带通峭度的改进谱峭度方法及在轴承诊断中的应用
2018-12-21毛志德杨世锡李兴林
张 龙, 毛志德, 杨世锡, 李兴林
(1. 浙江大学 机械工程学院, 杭州 330027; 2. 华东交通大学 机电与车辆工程学院, 南昌 330013;3. 杭州轴承试验研究中心 博士后工作站, 杭州 310022)
滚动轴承运行过程中,元件局部缺陷将与其它元件工作表面相接触,从而产生冲击。该冲击作用时间短、频域跨度大,从而可能激发轴承、轴承座和传感器系统的固有振动。该固有振动受阻尼作用,通常在下一个冲击到来之前几乎完全衰减,从而形成一个冲击响应链。冲击响应的发生频率由轴承转速及其尺寸参数确定,也称为故障特征频率。滚动轴承振动故障检测的目的就是从采集到的受噪声和其它机器部件干扰的振动信号中确定冲击的有无、强弱和发生频率,以此判断是否存在故障、故障程度及故障部位。共振解调方法是滚动轴承故障检测中常用的方法之一,利用带通滤波器在故障冲击引起的固有频率附近进行滤波,通过对滤波信号的包络信号进行频谱分析确定轴承健康状态。但带通滤波器中心频率和带宽参数的选择往往需要丰富的先验知识和历史数据,易造成较大的分析误差[1]。
谱峭度(Spectral Kurtosis, SK)最早由Dwyer提出并用于检测信号中非高斯分量的出现及所在谱线[2]。Antoni进一步完善了SK的理论基础且推广了其应用范围[3],并将SK方法中获得的最大峭度值作为状态监测指标值,以最大峭度值所在SK曲线为依据设计带通滤波器进行滚动轴承故障检测[4]。为提高SK的执行效率以适合工业现场使用,Antoni提出了基于FIR滤波器的快速谱峭度方法(Fast Spectral Kurtosis, FSK)[5]。此后,SK方法在故障诊断领域中广受关注,包括轴承[6-7]和齿轮[8-9]等的故障检测。理论上,带通滤波器中心频率和带宽参数的组合(f,Δf)有无限多种可能,但FSK以1/3-二进滤波器组方式对信号整个频带进行划分,减少了搜索空间和计算工作量,因此称为快速算法。
为进一步完善FSK的理论和实际应用效果,研究人员做了许多有益的改进工作。如Lei等以小波包分解替代FSK中的FIR滤波器,以获得更为精确的滤波结果[10]。考虑到FSK中用于度量滤波信号冲击特征提取效果的时域峭度指标容易受非高斯噪声和偶然性外界冲击的影响,从而导致频带选择错误的问题,Barszcz等提出了Protrugram方法,以滤波信号包络谱的峭度值作为评价指标[11]。Wang等结合小波包分解和包络谱峭度,提出了一种改进的谱峭度方法,以小波包节点信号的包络谱峭度最大来选择最优解调频带[12];同时Tse等还提出以包络谱的稀疏度作为评价指标[13]。事实上,FSK中的1/3-二进滤波器组能提供比小波包分解更为丰富的候选频带,而小波包分解容易遗漏位于两个子带接壤处的共振谱峰。同时当诊断对象包括轴承、齿轮和转子等部件时,根据包络谱峭度和稀疏度指标选择的频带包含的可能是齿轮或转子故障信息,而非轴承故障特征。针对上述问题,Zhang等保留FSK中的1/3-二进滤波器,但以最大相关峭度替代时域峭度和包络谱峭度,取得了较好的效果[14]。然而最大相关峭度受滤波器长度参数和解卷积周期参数影响严重[15]。
基于上述分析,本文提出一种基于包络谱带通峭度的改进谱峭度方法。该方同样保留了原始FSK方法中的1/3-二进滤波器方式,以便更全面地搜索频域空间。为了避免齿轮和转子等转频类故障带来的影响,同时考虑到包络信号的低频特性,对滤波信号的包络谱进行加窗处理,只计算包络谱中间段的峭度值。这种操作类似带通滤波,因此称为包络谱带通峭度,区别于文献[11-12]中的包络谱峭度。以一个包含轴承和齿轮局部故障特征的仿真信号和实验台信号验证本文方法的有效性。
1 方法介绍
1.1 谱峭度
峭度是描述波形尖峰度的一个指标,对冲击信号非常敏感,可以对信号非平稳强弱进行评判。但早期故障中信噪比很低,峭度作为一个全局指标不能正确地反应出故障类型,不适用于强噪声干扰环境下的故障检测。Dwyer提出的SK方法实际上是计算每一条谱线上信号的非平稳特性来确定非平稳特征所在的频率。前人研究表明该方法能够很好地提取出被噪声淹没的故障信号,同时还能表示故障相应频率的峭度值。假设信号y(t)如下

(1)
式中:H(t,f)为被分析信号x(t)的时频复包络;可采用短时傅里叶变换计算或Antoni提出的基于带通滤波的谱峭度快速计算方法得到。根据谱的阶矩定义,谱峭度表示如下
(2)
式中:C4y(f)为信号y(t)的四阶谱累积量;S(f)为谱瞬时矩。假设实测振动信号为z(t)
z(t)=x(t)+N(t)
(3)
式中:x(t)为故障信号;N(t)为噪声信号。运行过程中,滚动轴承元件与局部缺陷接触时会产生冲击,引起整个系统的共振,所得故障信号x(t)的通用模型如下
(4)
式中:h(t)为单个脉冲的脉冲响应;Ak和τk分别为各个脉冲的幅值和发生时间。
为了体现谱峭度方法在诊断过程中滤波效果,将其解释为理想滤波器组输出结果在频率f处的峭度值,如式(5)所示
(5)
式中:KZ(f)与Kx(f)分别为实测信号和故障信号的谱峭度;ρ(f)为信噪比的倒数。因此,某一频率处信噪比高,则表示该处实测信号的谱峭度近似等于故障信号的谱峭度,从而可以找出最优滤波频带。
1.2 包络谱带通峭度
设原始信号为x(t),经过1/3-二进滤波器中某一滤波器滤波后的信号为xfiltered(t),则滤波信号的解析信号如下式所示
(6)

(7)
设滤波信号包络Env(t)的离散形式为Env(n),n=1, 2, …,N(N为信号长度,偶数),相应的包络谱为
m=0,1,…,N-1
(8)
设轴的旋转频率为fr,信号采样频率为fs。为了准确找出滚动轴承故障特征,需要排除转频类故障(转子碰摩、齿轮局部缺陷等)的影响,在计算包络谱峭度时必须将小于a×fr部分排除在外,a为考虑的转频谐波倍数。由采样频率和信号长度可知频谱分辨率Δf为
(9)
因此,a×fr对应的谱线为

NUM1=afrΔf=2afrNfs
(10)
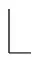
当轴承存在局部缺陷时,希望除了找到故障特征频率外,还能找到二阶、三阶或者更高阶的谐波分量[16]。因而可以将包络谱加窗截取的上限设置为4倍最大故障特征频率。通常情况下轴承外圈固定在轴承座内,而内圈随轴一起转动,此时最大故障特征频率为内圈故障特征频率(Ball Passing Frequency Inner Race, BPFI),因此可以固定包络谱峭度计算范围的上限为4×BPFI,对应的谱线为NUMu。

NUMu=4BPFIΔf=8N×BPFIfs
(11)

如式(12)所示,包络谱带通峭度(Kurtosis of both-ends truncated envelop spectrum, Kurt_btes)即在[NUMl,NUMu]范围内计算包络谱V(m)的峭度。
(12)
1.3 基于包络谱带通峭度的改进谱峭度方法
本文对快速谱峭度方法的改进主要体现在以式(12)的包络谱带通峭度替代原始方法中的时域峭度,同时考虑到带通滤波器宽度太窄时,将不能包含轴承故障引起的调制边带。带通滤波器宽度至少应该包含3倍的轴承最大故障特征频率(通常为BPFI),因此对快速谱峭度分解的最大层数Nlevel进行限制,层数取值范围[0, 1, 1.6, 2, 2.6, 3, …]。

Nlevel=log2fs6BPFI()
(13)
本文提出的基于包络谱带通峭度的改进谱峭度方法流程,如图1所示。首先根据轴承参数和转速得到内圈故障特征频率BPFI,进一步结合采样频率由式(13)确定轴承分解层数。采用1/3-二进滤波方式,按照确定的分解层数对信号进行滤波,根据式(12)计算各滤波信号的包络谱带通滤波峭度值Kurt_btes,并生成直观的改进谱峭度图。最后选择最大包络谱带通峭度值(Kurt_btes)对应频带的滤波信号进行包络谱分析,确定轴承有无故障或故障类型。

图1 本方法流程图
2 仿真信号分析
齿轮箱是工业现场应用非常广泛的一种机械传动装置,因工作负荷大、长时间连续运转以及工作环境恶劣等因素而易发生齿轮和轴承故障。本节利用仿真信号模拟一个一级减速齿轮箱同时发生齿轮断齿故障和滚动轴承外圈局部故障的情况,检验本文提出的基于包络谱带通峭度的改进谱峭度方法能否在齿轮故障干扰下准确检测到滚动轴承故障。
齿轮减速箱内大小齿轮的齿数分别为33和22,在小齿轮的某个齿上设置断齿故障,以使得混合信号中齿轮故障占绝对优势。电机驱动小齿轮以600 r/min的转速旋转,建立如文献[17]所示的5-DOF齿轮动力学模型。采样频率设置为Fs=5 000 Hz,得到齿轮箱体上的振动加速度信号,如图2所示。从图2可知,2 s内共有20个冲击存在,与小齿轮旋转频率一致,符合断齿故障特征。

图2 轮齿断齿故障仿真信号
根据文献[18]对滚动轴承外圈故障信号进行仿真,外圈轴承故障特征频率40 Hz,故障冲击激起的固有频率为2 000 Hz,冲击响应按指数函数规律衰减,衰减系数600。设置采样频率为5 000 Hz,得到仿真信号,如图3(a)所示。为了模拟早期故障,加入幅值为0.2的随机噪声后得到信号,如图3(b)所示。考虑到本文目的在于检验所提出的改进谱峭度方法的优越性,因此不过多讨论齿轮箱动力学建模问题,仅将图2的齿轮振动信号与图3(b)的轴承外圈早期故障信号进行相加合成,以模拟齿轮箱整体振动情况。所得最终合成信号,如图4所示。由于齿轮断齿属于严重故障而轴承处于早期故障阶段,合成信号中齿轮缺陷导致的冲击占明显优势。
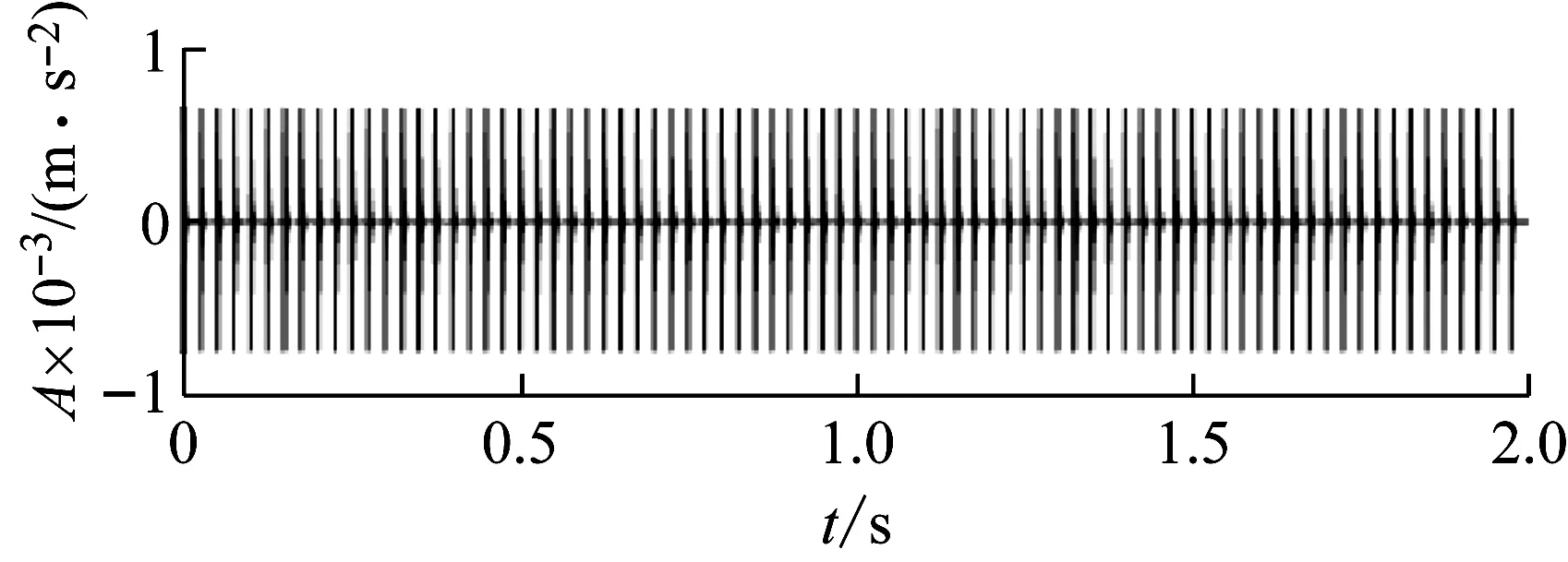
(a) 未加噪声的外圈仿真信号

(b) 加噪后的外圈仿真信号

图4 轴承齿轮混合信号
利用原始谱峭度方法和本文提出的改进谱峭度方法对图4的合成信号进行分析,所得的谱峭度图和最优包络谱,分别如图5和图6所示。由图5(a)可知,原始谱峭度方法得到的最优解调频带为[0,1 250]Hz,图5(b)的包络谱显示该方法能检测到齿轮故障,但未能反映轴承故障特征信息。分析其原因如下:① 齿轮局部故障如齿面剥落、齿根裂纹和断齿等通常表现为以啮合频率及其谐波为载波频率,故障冲击对应调制频率的调频调幅信号。而齿轮啮合频率为22×600 r/min=220 Hz,因此[0,1 250]Hz包含了啮合频率及其二次、三次直至五次谐波在内的载波频率;② 齿轮故障导致的脉冲比轴承故障脉冲更稀疏且幅值更大,因此峭度值更大。上述便是以滤波信号时域峭度最大为目标的原始谱峭度方法选择[0,1 250]Hz作为滤波解调频带并检测出齿轮故障而不能诊断出轴承故障的原因。
本文的改进谱峭度方法计算滤波信号包络谱在[2×fr,4×BPFI]范围内的峭度值,因此与转频相关的齿轮和转子局部故障不会影响轴承故障检测。如图6(a)所示,改进后的谱峭度图中最优滤波频带为[1 666,2 500]Hz,该范围包含了轴承故障模拟信号中的2 000 Hz共振频率,同时带宽834 Hz能够包含足够多的故障边频带。从图6(b)的最优频带包络谱中可见轴承外圈故障特征频率及其多阶谐波分量,说明改进的谱峭度方法能在齿轮强故障干扰下检测出轴承早期故障。同时也说明将本文改进方法与原始谱峭度方法联合使用,能诊断出轴承和齿轮复合故障。

(a) 混合信号原始谱峭度图

(b) 混合信号原始谱峭度图
3 实验数据分析
3.1 含偶然性冲击的故障信号分析

(a) 混合信号改进谱峭度图

(b) 包络谱
本节分析偶然性冲击对谱峭度检测方法的影响,实验信号来自图7所示的自制转子-轴承故障实验台。实验台包括伺服电机及其控制器、支撑轴承、圆盘与轴、故障轴承以及振动加速度信号采集系统。左端故障轴承型号为N205,通过线切割技术在其外圈滚道加工一条宽0.5 mm的凹槽来模拟外圈局部故障。转速为1 000 r/min时,以12 000 Hz的采样频率采集1 s数据,如图8(a)所示。此时轴承外圈故障特征频率BPFO=87.51 Hz。由于实验测试干扰小,图8(a)中故障冲击非常明显。为模拟工程实际中的外界干扰,首先在信号中加入幅值为4的高斯噪声,得到含噪信号,如图8(b)所示。进一步在信号2 281到2 360点范围内叠加幅值为60的随机噪声,模拟外界偶然性干扰冲击,最终加入噪声和冲击的信号,如图8(c)所示。从图8(c)可知,偶然性冲击占绝对优势,周期性故障冲击已不明显。

图7 滚动轴承故障实验台

(a) 采集的原始加速度信号

(b) 加入噪声和干扰冲击后的加速度信号

(c) 加入噪声和干扰冲击后的加速度信号

(a) 加入噪声和脉冲干扰后的原始谱峭度图

(b) 包络信号

(c) 包络谱
首先利用原始谱峭度方法对图8(c)的信号进行分析,由于其没有自动确定分解层数的功能,此处人为设置分解层数为4。所得谱峭度图如图9(a)所示。所选择的最佳滤波频带为[4 500, 6 000]Hz,滤波所得信号的包络如图9(b)所示。其中偶然性冲击突出,未见明显轴承周期性故障冲击。对包络信号进行频谱分析,得到图9(c)的包络谱中没有显著的频率成分,无法检测到轴承故障。说明偶然性冲击会误导原始谱峭度方法,从而选择不恰当的频带进行滤波解调。原因在于对时域峭度而言,冲击越稀疏、冲击幅值越大,则峭度值越大,峭度在原理上没有考虑冲击的周期性。
实验轴承内圈故障特征频率BPFI=129.15 Hz,根据式(13)可知分解层数Nlevel=3。本文方法所得改进谱峭度图如图10(a)所示,可知所选择的最优滤波频带为[3 000, 4 000]Hz。偶然性冲击因为持续时间短(仅6.7 ms)、幅值大,几乎存在于整个分析频段。因此无论选择哪个频段进行滤波,其中都存在偶然性冲击的影响,关键在于同时要能得到故障引起的周期性冲击。[3 000, 4 000]Hz频段滤波后信号的包络,如图10(b)所示。不仅存在偶然性冲击,而且也存在明显的轴承故障周期性冲击成分。所得包络谱,如图10(c)所示。其中频率成分87.09 Hz与轴承外圈故障特征频率BPFO=87.51 Hz接近,说明本文方法在偶然性冲击干扰下仍能检测出轴承故障。

(b) 包络信号
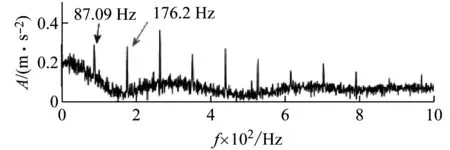
(c) 包络谱
3.2 轴承疲劳实验数据分析
本节对轴承从完好状态一直运行到发生故障直至使机器停机的疲劳过程实验数据进行分析,以验证本文提出的改进谱峭度方法在轴承全寿命周期过程中及时发现早期故障的能力。相比于上节所述的人工植入故障,疲劳实验数据更能模拟轴承实际应用中的故障发生和发展。
数据来自辛辛那提大学智能维护系统中心[19]。实验台结构,如图11所示。电机以皮带传动方式驱动主轴以2 000 r/min的转速旋转,主轴上装有四个型号为Rexnord ZA-2115的双列滚子轴承。为了缩短轴承失效时间,在主轴中间轴承座2和3上施加2 721.6 kg的径向载荷。由轴承参数和转速可知轴承内圈故障特征频率BPFI=297.9 Hz,外圈故障特征频率BPFO=236.4 Hz。疲劳实验时间为2004-02-12T10:32/2004-02-19T06:22。实验结束时发现轴承1外圈损伤严重。实验过程中利用NI DAQ Card 6062E采集卡每隔10 min以采样频率20 kHz采集一次长为20 480点的振动信号,整个实验过程共采集到984个实验数据文件,每个文件包含4列数据,本文分别对数据文件的第一列和第二列进行分析,该两列数据分别由安装在轴承1和轴承2上的传感器采集。

图11 疲劳寿命试验台结构示意图
振动加速度信号有效值(RMS)能够反应轴承振动的剧烈程度,常用于表征轴承故障程度。轴承全寿命周期内数据文件第一列和第二列的RMS变化趋势,分别如图12(a)和图12(b)所示。从图可知,第一列数据的RMS在第534个文件处发生突变,第二列数据则在703个文件处发生突变。第一列数据由安装在最终发生故障的轴承1上的传感器采集,因此可以认为轴承1发生早期故障的文件序号为534。在轴承2上采集的第二列数据由于距离故障轴承较远,振动衰减导致其RMS只能在文件序号为703时发现故障。由于工程实际中难于在每个轴承的轴承座上安装传感器,因此对故障轴承附近的传感器信号进行分析也是必要的。第534个文件第一列数据波形和第703个文件第二列数据波形分别如图12(c)和图12(d)所示。从图中均无法搜索到明显的轴承故障冲击,因此需要采取合适的信号处理方法进行分析。

(a) 疲劳试验全寿命周期RMS演化-第一列数据

(b) 疲劳试验全寿命周期RMS演化-第二列数据

(c) 第534个文件的第一列数据时域波形

(d) 第703个文件的第二列数据时域波形
已知轴承内圈故障特征频率和采样频率,根据式(13)可知分解层数Nlevel=3。首先利用原始谱峭度方法对第534个文件的第一列数据进行分析,得到图13(a)所示的谱峭度图。可知所选择的最佳滤波频带为[6 667, 8 333]Hz。所得滤波后的信号包络,如图13(b)所示。从图13(b)可知,一个类似偶然性冲击成分显得非常突出。如表1所示,该冲击对应包络线最大值0.057 6,而包络线的均值为0.009 8,且仅有此一处大幅值异常冲击,由此导致基于时域包络峭度的原始谱峭度方法将该频段作为最优滤波段。对包络做频谱,得到包络谱,如图13(c)所示。从图13(c)可知,与外圈故障特征频率BPFO=236.4 Hz接近的频率成分230.2 Hz,可以初步断定轴承发生外圈故障,但缺少倍频成分作为辅证。230.2 Hz与BPFO之间的差异主要是由于轴承打滑、间隙和转速波动等原因造成。
利用本文提出的改进谱峭度方法对上述信号进行分析,所得谱峭度图如图14(a)所示。所选最佳滤波频段为[5 000, 10 000]Hz。所得滤波信号包络,如图14(b)所示。没有明显突出的冲击成分,因此其时域包络峭度值4.372 7<图13(b)包络的峭度值6.656 9。得到包络谱,如图14(c)。其中存在与BPFO接近的230.6 Hz频率成分及其二倍频和三倍频。相比图13(c),轴承外圈故障特征更为明显。
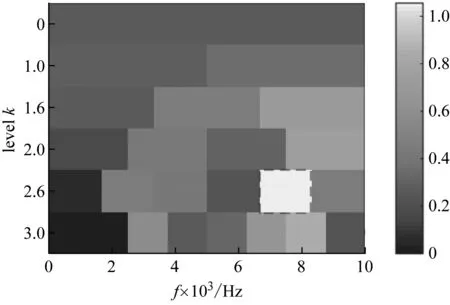
(a) 第534个文件第一列数据的原始谱峭度图

(b) 滤波后的信号包络

(c) 包络谱

滤波频段/Hz[6 667, 8 333][5 000, 10 000]时域包络峭度6.656 94.372 7包络谱带通峭度14.751 745.463 7包络信号最大值0.057 60.134 6包络信号均值0.009 80.032 7

(a) 第534个文件第一列数据的原始谱峭度图
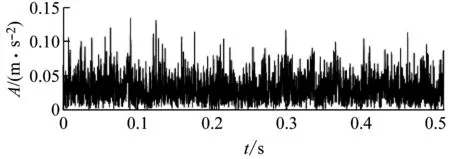
(b) 滤波后的信号包络
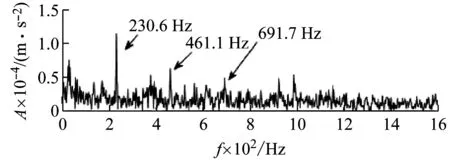
(c) 包络谱
第二列数据由安装在与故障轴承1相邻的轴承2上的传感器采集,因信号传递衰减,其RMS显示其能最早发现轴承故障的时刻为第703个文件处。利用原始谱峭度方法和本文提出的改进谱峭度方法对第703个文件的第二列数据进行分析,两者所得结果,分别如图15和图16所示。从所得包络谱可知,原始谱峭度方法的包络谱中不存在任何轴承故障特征频率相关成分,而图16(c)的改进谱峭度方法的包络谱中存在与外圈故障特征频率BPFO接近的频率成分及其倍频,可确诊外圈故障。原始谱峭度方法以滤波信号的时域包络峭度作为滤波频带选择准则,图15(b)的包络信号中存在稀疏大幅值冲击。如表2所示,包络信号最大值为0.139 7、均值为0.024 8。与图16(b)相比,两者均值几乎一样,但前者最大值大于后者,从而导致图15(b)包络信号峭度值>图16(b)的包络信号峭度值。

表2 第703个文件第二列数据的不同滤波频段结果

(a) 第703个数据文件的原始谱峭度图
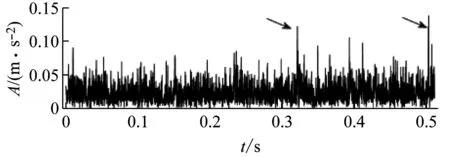
(b) 滤波信号的包络

(c) 包络谱
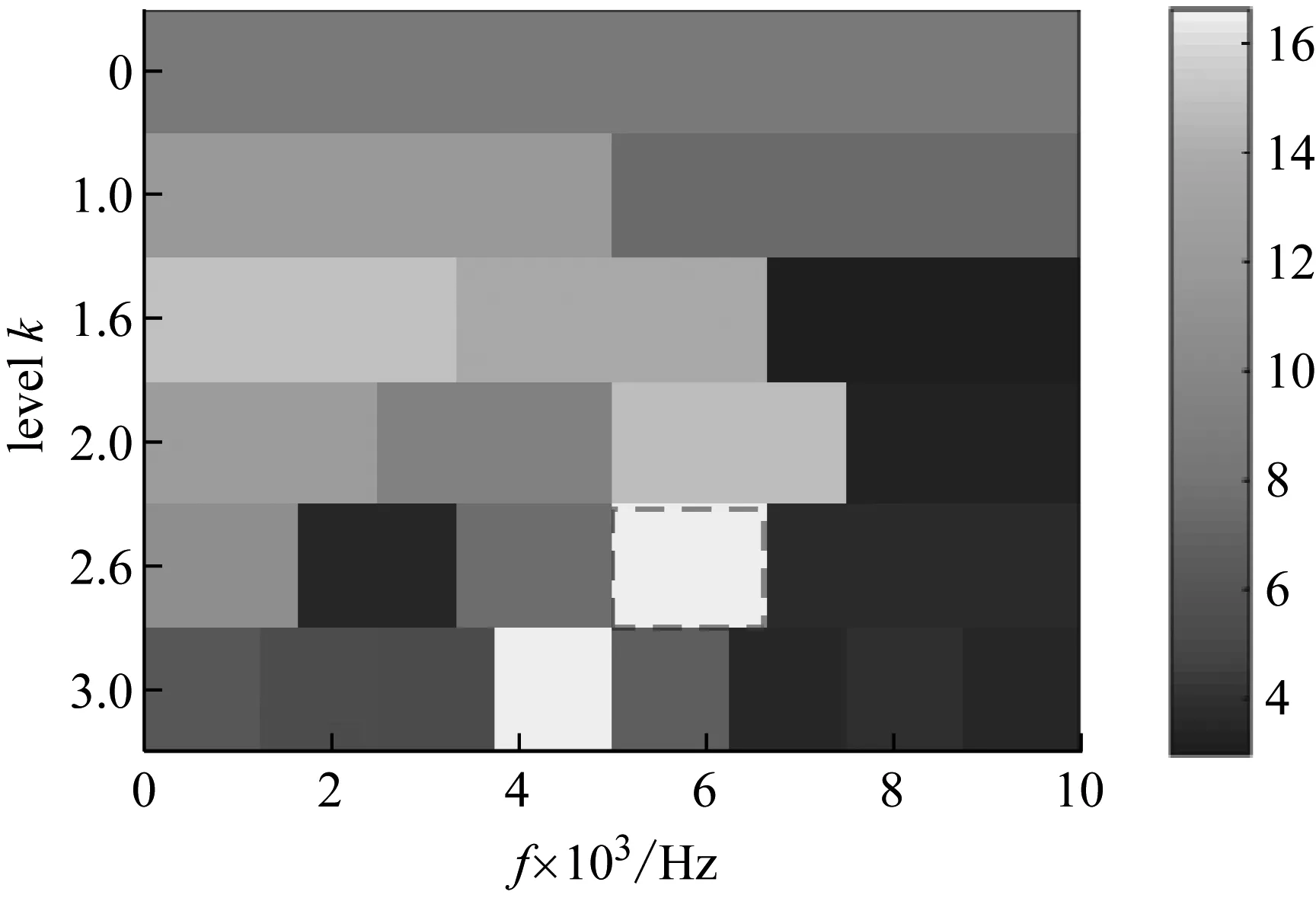
(a) 第703个数据文件的改进谱峭度图

(b) 滤波后的信号包络
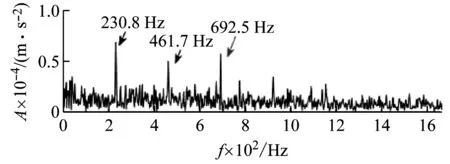
(c) 包络谱
原始谱峭度方法不能找到故障特征的根本原因在于时域包络峭度仅考虑了冲击性强弱,但没有考虑到冲击发生的周期性特征,这正是本文研究的出发点。
4 结 论
针对原始谱峭度方法中采用的时域包络峭度易受外界偶然性冲击干扰以及齿轮和转子冲击故障影响,而无法有效检测轴承局部故障的问题,提出利用滤波信号包络谱带通峭度衡量带通滤波器效果。包络谱带通峭度指截去包络谱低频段(齿轮和转子冲击故障特征位于此频段)和高频段(高频噪声所在频段)后,只计算包络谱中间段的峭度值。仿真信号、人工植入故障信号以及疲劳试验数据分析表明:
(1) 基于包络谱带通峭度的改进谱峭度方法能够有效排除齿轮故障冲击和外界偶然性冲击干扰的影响,从而有效检测轴承局部故障;
(2) 在存在齿轮、转子和轴承复合故障时,原始谱峭度方法能够有效提取齿轮和转子局部故障导致的低频冲击特征,而本文的改进谱峭度方法能有效检测轴承局部故障导致的高频冲击特征,因此两者结合有望能诊断出复合故障;
(3) 疲劳实验数据分析说明本文方法较原始谱峭度方法在监测轴承早期故障方面更具优势。
