基于整车分析的磁流变减振器优化研究
2018-12-21韩佐悦余春贤
李 静, 韩佐悦, 周 瑜, 余春贤
(吉林大学 汽车仿真与控制国家重点实验室, 吉林 长春 130022)
半主动悬架可以有效抑制车身振动,提高车辆平顺性,并以其低成本低能耗的特点得到了广泛的研究和应用。在各种类型半主动悬架执行器中,磁流变减振器(Magneto-Rheological Damper, MRD)因其响应快速、控制灵活等特点,近年来成为重要的研究方向。国内外学者对MRD的设计及优化进行了大量研究。
Guglielmino等[1]在其专著中系统的分析了MRD设计流程,将其拆分为流体参数设计与线圈参数设计,以动态系数最大为目标确定结构尺寸,进而根据磁场需求计算线圈参数。 Sung等国内外学者则基于有限元仿真方式,分别以最大阻尼力[2-3]、最小控制能量[4]、最大动态系数[5]、最小活塞体积[6]、最大磁感应强度[7-8]为目标,对MRD活塞设计参数进行了优化分析。
MRD设计过程中存在流体、磁场、电气特性参数相互耦合的现象,而以上研究中单一目标优化无法获得全局最优解。针对此问题,国内外学者进行了多目标优化研究。Hadadian等[9-10]以最大阻尼力、动态系数及感应时间常数的加权值最小为优化目标,优化活塞参数。郑玲等将响应时间常数与功率加权为目标函数,以铁芯磁感应强度为约束条件,优化活塞参数[11]。董小闵等以最大阻尼力、可调系数、温度评价系数加权为目标,优化活塞参数[12]。
以上研究的设计过程用于车用MRD设计均存在不足:MRD的最大阻尼力、最小阻尼力、动态系数、响应时间等指标均通过设计参数高度耦合,单独选取或简单线性加权均难以全面且准确地描述磁流变减振器特性,也无法与车辆半主动悬架性能进行匹配;现有的MRD优化往往将设计参数作为独立变量来进行设计域中的自由搜索,忽略了磁场及几何约束,优化范围过大,不够高效。
针对以上问题,对车用双线圈单筒纯流动模式MRD进行设计优化,全面分析了MRD动力学特性,并梳理了几何、磁场、电路中各设计参数间的约束关系,筛选出核心设计参数。针对磁场环境中的重要参数基于磁场特性设计其动态约束条件,基于有限元仿真及神经网络拟合参数边界模型,缩小优化范围。设计并优化了基于天棚阻尼控制的多参数反馈整车控制算法。创建包含整车模型、控制器模型、减振器模型、执行器响应模型的联合仿真平台,使用遗传算法对减振器设计参数进行优化。
1 MRD设计参数约束分析
1.1 MRD动力学模型
设计的某自主中级轿车MRD结构,如图1所示。
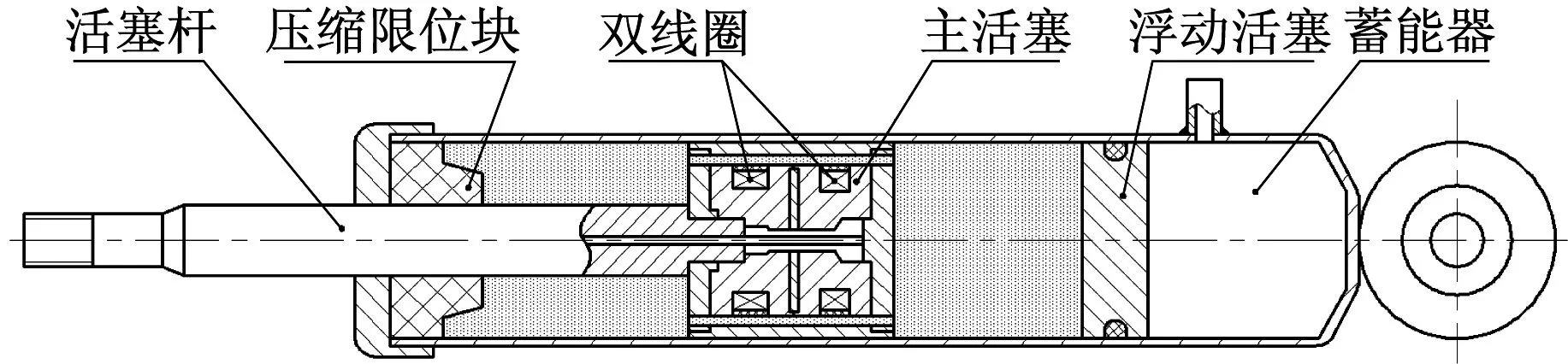
图1 双线圈单筒磁流变减振器结构
在车辆悬架系统中,悬架作用于车身的力为
Fsus=Fspr+Fη+Fτ+Fg+Fbump
(1)
式中:Fsus为悬架总作用力;Fspr为悬架弹簧作用力;Fη为MRD黏性阻尼力;Fτ为MRD磁致阻尼力;Fg为蓄能器作用力;Fbump为悬架行程限位块作用力。
选用MR140CG型磁流变液,基于其黏度特性,将磁流变液简化为Bingham模型,并将磁流变液流动近似为牛顿层流,则Fτ与Fη可以表示为
(2)
(3)
式中:c为MRD磁致阻尼系数,取2.07;A1为减振器有杆侧活塞面积;g为活塞油液通道宽度;τy为磁流变液剪切屈服应力;Lmp为活塞内有效磁极长度;μ0为磁流变液无磁场黏度;Lpt为活塞总长度;r1为油液通道中心圆半径;vp为活塞运动速度。
将蓄能器内气体近似为理想气体,且忽略缸筒变形,则Fg可以表示为
(4)
式中:Pg0为初始状态蓄能器中气体压力;Ar为活塞杆截面积;sp为减振器活塞位移;Vg0为初始状态蓄能器体积;Vg0=Lgc(A1+Ar);Lgc为蓄能器长度。
MRD的稳态输出范围,如图2中灰色区域所示。
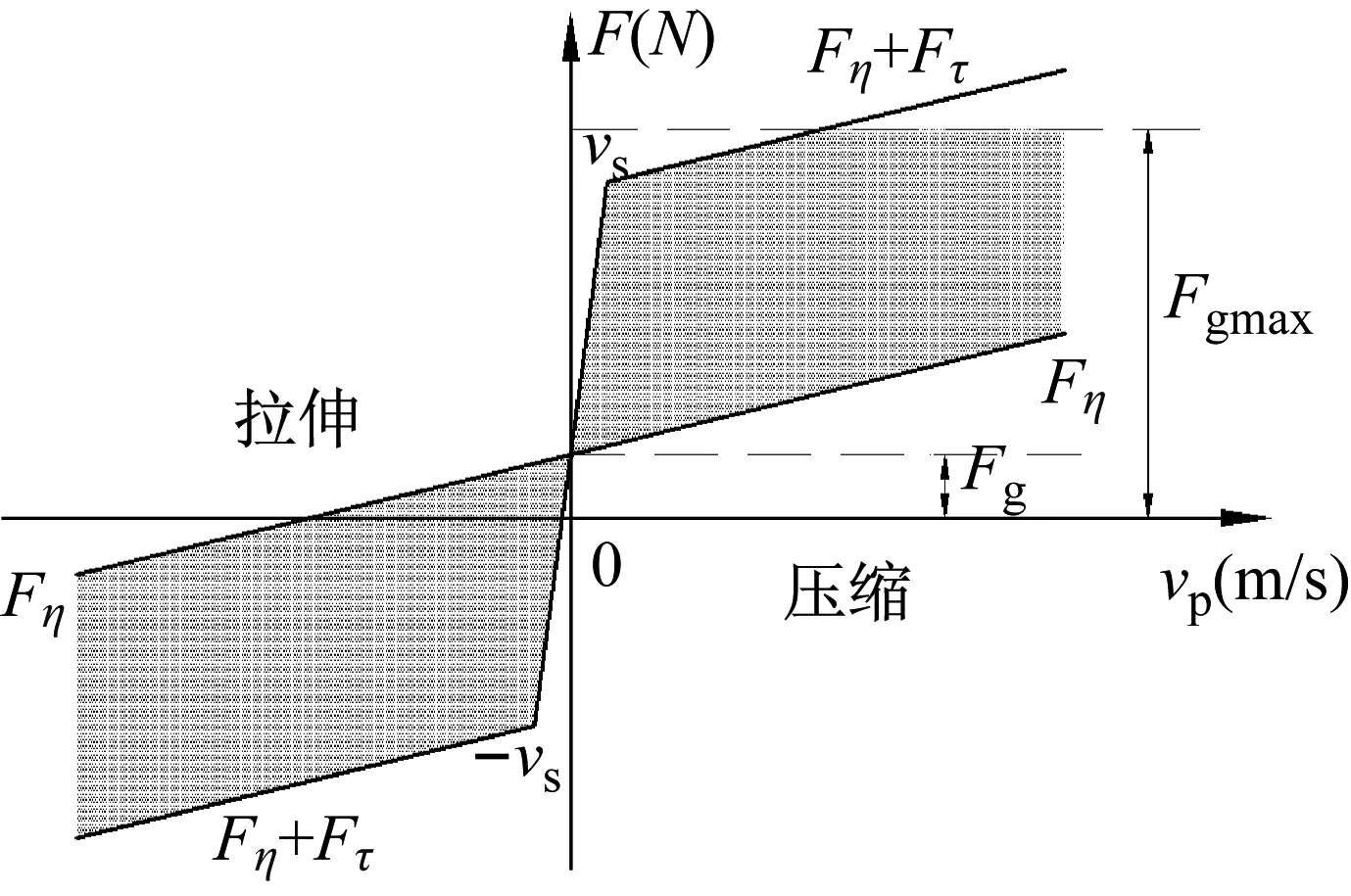
图2 MRD输出力范围
1.2 MRD设计参数约束条件分析
MRD设计参数的约束条件分为几何约束、磁场约束、响应约束及功率约束。
几何约束方面,设计参数的长度方向约束条件为
Ld=Lfix+Lgpt+Lpt+Lgc+Lre+Lbu
(5)
式中:Ld为MRD筒体长度;Lfix为包括安装长度及密封件厚度在内的固定长度;Lgpt为浮动活塞长度;Lre为MRD拉伸行程长度;Lbu为MRD压缩行程长度。
减振器主活塞内结构及设计参数,如图3所示。
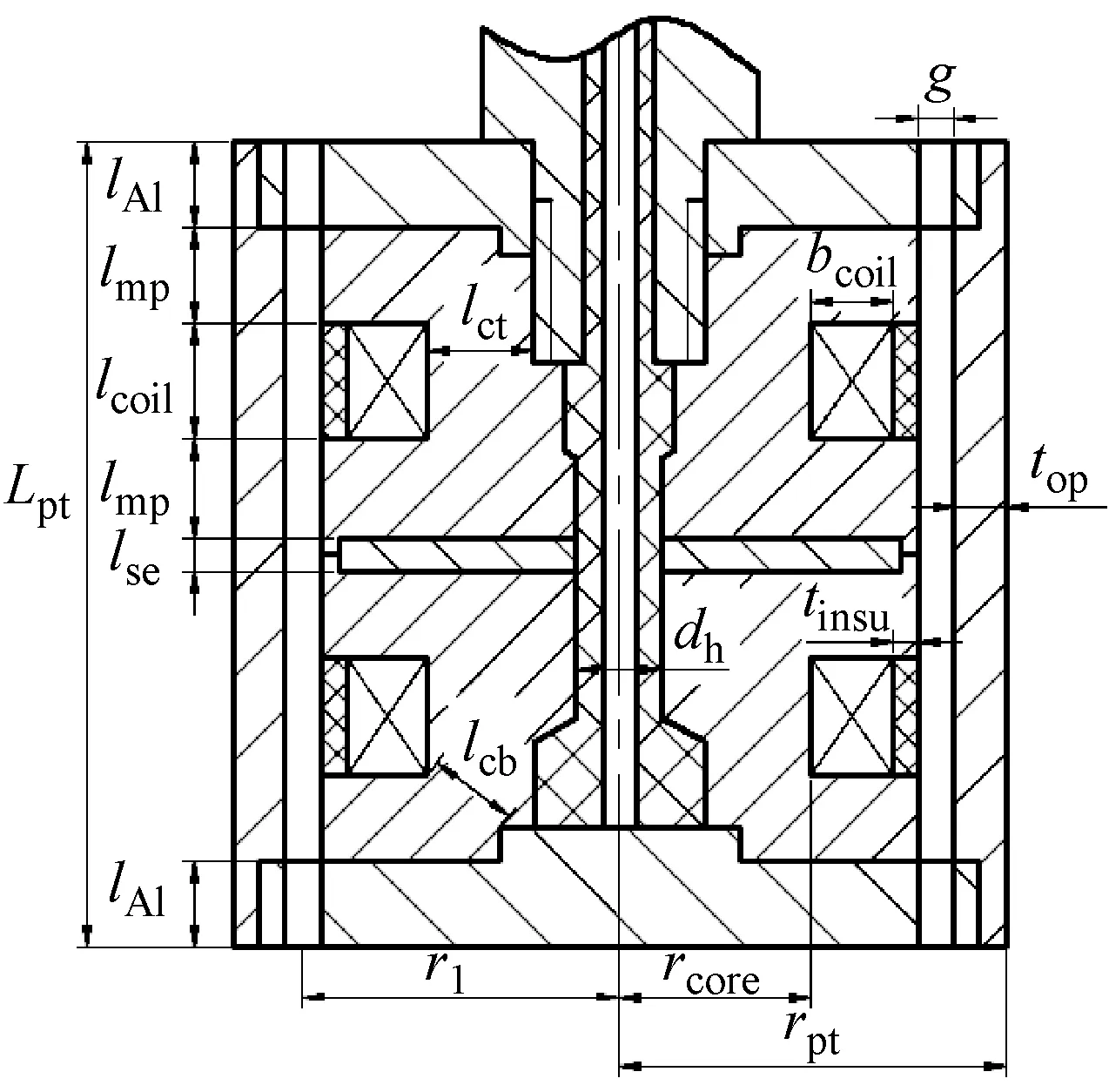
图3 主活塞内部结构与设计参数
活塞内长度约束条件
Lpt=4lmp+2lcoil+2lAl+lse
(6)
式中:lmp为单磁极长度;lcoil为单线圈轴向长度;lAl为活塞两端挡板厚度;lse为活塞内隔离板厚度。
车辆悬架由传统减振器更换MRD时,由于活塞及蓄能器轴向尺寸增加导致可用行程降低,为满足相同悬架缓冲能力,需对压缩行程限位块进行调整,满足
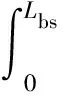
(7)
式中:Fspr为弹簧力;Fb为限位块作用力;Lbs传统减振器压缩行程。
设计参数径向约束条件为
rpt=dh/2+(rcore-rh)+bcoil+tinsu+g+top
(8)
式中:rpt为MRD活塞外径;dh为铁芯中心孔直径;rcore为励磁铁芯线圈处半径;bcoil为线圈径向厚度;tinsu为线圈外部绝缘层厚度;g为油液通道间隙;top为活塞外筒厚度。
线圈部分几何约束条件为
(9)
式中:ηcoil为线圈绕制填充率,ncoil为单个线圈匝数,ηcop为漆包线铜芯面积占比,Jmax为线圈最大许用载流密度,icoil线圈工作电流。
式(9)代入线圈电阻计算公式及欧姆定律,得到漆包线截面约束条件
Awire=2πbcoilrcoilJwireηcoilρcoprcoil(ncoil)/Ucoil
(10)
式中:ρcop为漆包线电阻率,rcoil为线圈等效中心圆半径,Jwire为线圈使用时的载流密度,Ucoil为稳态情况下的单线圈上的压降,Awire为漆包线截面积。
磁场约束方面,为避免材料磁场饱和,活塞外筒几何尺寸应满足
(11)
式中:Bmp为磁极处平均磁感应强度;Bsat为活塞外筒材料饱和磁感应强度。
同理,rcore应满足
(12)
基于基尔霍夫第二定律,线圈的励磁能力应满足
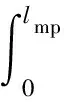
(13)
式中:Rm为磁路各部分的总磁阻。
响应约束方面,MRD电气特性可以近似简化成等效电感串联电阻模型[13],其中线圈等效电感Lcoil为
(14)
式中:φ为单磁极上的磁通量;μdmp为活塞等效磁导率,lcore为单个线圈磁场回路的等效磁路长度。
减振器电气特性传递函数可表示为
(15)
式中:Udmp为MRD两端电压;Rcoil为线圈电阻,Rcable为与线圈串联导体部分电阻。
功率约束方面,在MRD线性区内,可调阻尼力与安匝数成正比,得到产生相同可调阻尼力所需功率
(16)
式中:kdmp为可调阻尼力生成系数。
整理上述约束条件及动力学关系,得到磁流变减振器设计参数约束关系,如图4所示。
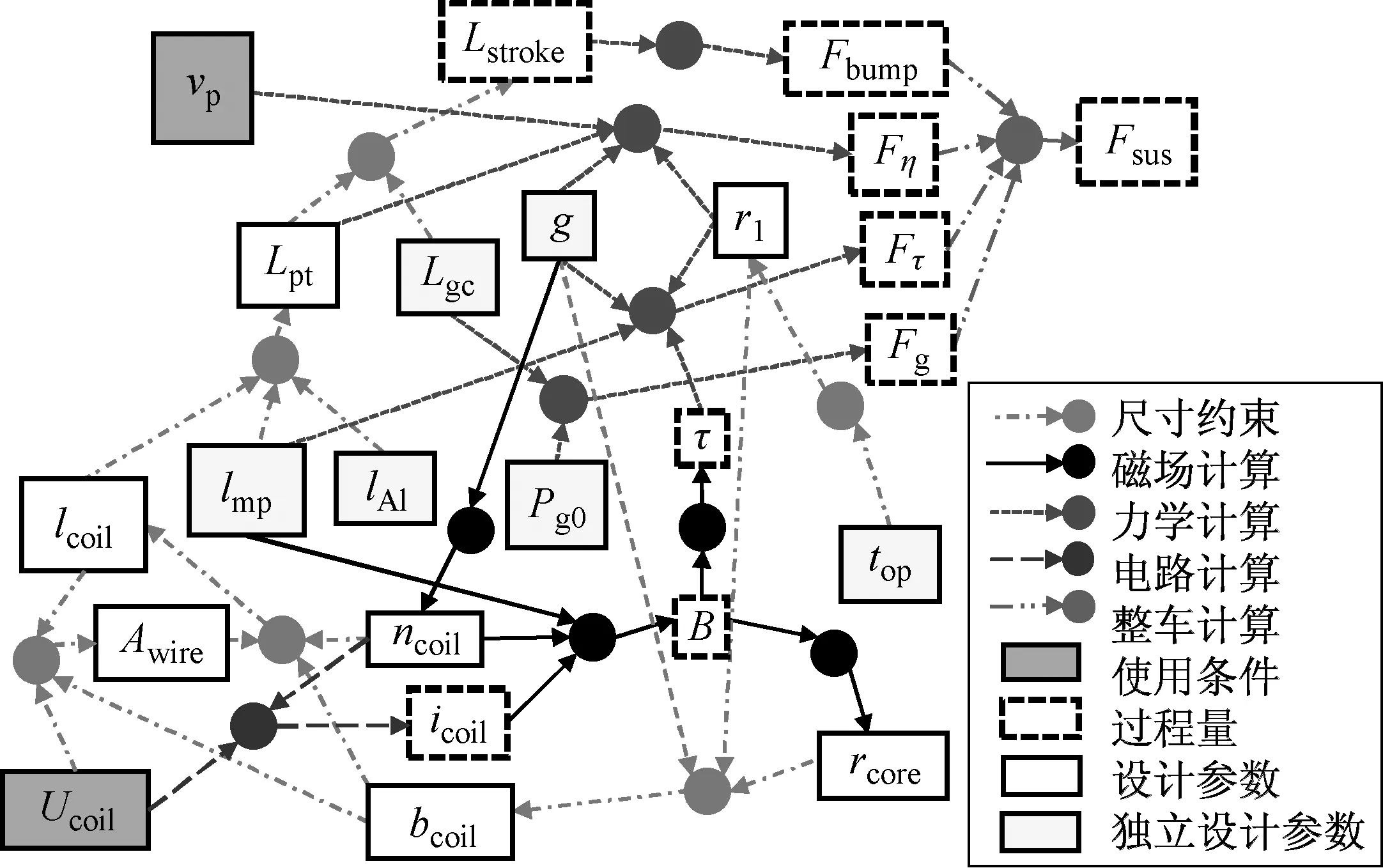
图4 MRD设计参数约束关系
各参数中Lmp、LAl、Lgc、g、Pg0、top为可独立取值的输入设计参数,其他参数取值范围均存在相互耦合关系。参数ncoil、Lmp、r1、g、Lgc、rcore涉及多个环节设计计算,且大部分取值与整车性能并非单调关系,如相同安匝数下,减小ncoil可有效提高减振器响应速度并减小活塞尺寸,但导致减振器功率Pdmp增加;g减小可以有效降低对线圈安匝数的需求,改善MRD响应特性,但会造成MRD黏性阻尼力与磁致阻尼力同时增大,偏离使用范围,恶化控制性能。现有研究均没有将约束关系完全解耦并得到全局最优组合。
因此本文在整车仿真环境下进行MRD参数优化,选取独立设计参数Lmp、Lgc、g、Pg0、top以及涉及多环节计算的ncoil、rcore作为MRD核心设计参数,通过几何约束条件计算其他参数,并通过动力学模型、执行器响应模型将参数耦合关系引入仿真模型,加入整车控制算法后进行整车仿真,以整车平顺性为指标进行MRD参数优化。
2 磁场设计参数的动态约束拟合
核心设计参数中除rcore外的其他参数均涉及动力学模型及整车仿真环节,需通过整车仿真进行优化。
rcore对主活塞内的磁场生成具有重要影响,其值较小则极易在铁芯中心处产生磁场饱和限制励磁效果,若较大则导致线圈厚度不足活塞过长,限制悬架行程。而rcore取值范围受其他设计参数影响,如能基于磁场分布特性拟合rcore的动态约束条件,可显著减小整车仿真环节设计参数寻优范围。
由于磁场的不均匀分布导致式(12)计算出的rcore很难代表实际铁芯磁场情况,因此基于有限元仿真,采用神经网络模型对rcore取值范围进行拟合。
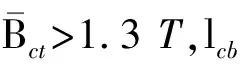
首先基于有限元仿真创建磁场分布参数拟合模型
Lb1=f(rcore,ncoil,g,Lmp,top,4A)
Lb2=f(rcore,ncoil,g,Lmp,top,4A)
(17)
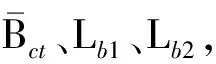
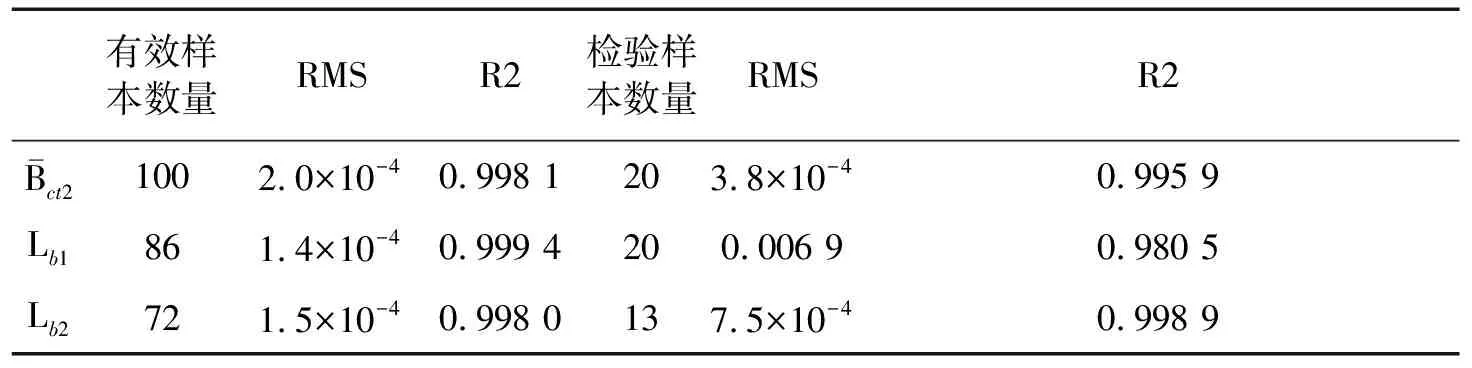
表1 磁场分布参数拟合结果
将获得的rcmax、rcmin与100组拟合样本中其他参数分别组合成新的拟合参数样本,采用神经网络拟合rcmax、rcmin的计算模型
(18)
最终rcmax的拟合优度为0.996 4,rcmin的拟合优度为0.996 1。
由于进行了两步神经网络拟合,为验证拟合精度,采用拉丁超立方重新生成20组参数样本,通过神经网络生成rcmax、rcmin,并通过有限元仿真进行验证和修正,得到的验证结果,如图5所示。

(a) rcmin拟合结果(b) rcmax拟合结果
图5rcore边界值神经网络模型拟合精度
Fig.5 Neural fitting precision ofrcorelimit
神经网络模型可以较好的模拟rcore取值范围,拟合误差可以控制在<0.2 mm。对100组样本计算结果进行±0.2 mm修正后,如图6所示,拟合模型将参数rcore的取值范围平均缩小了79.7%。
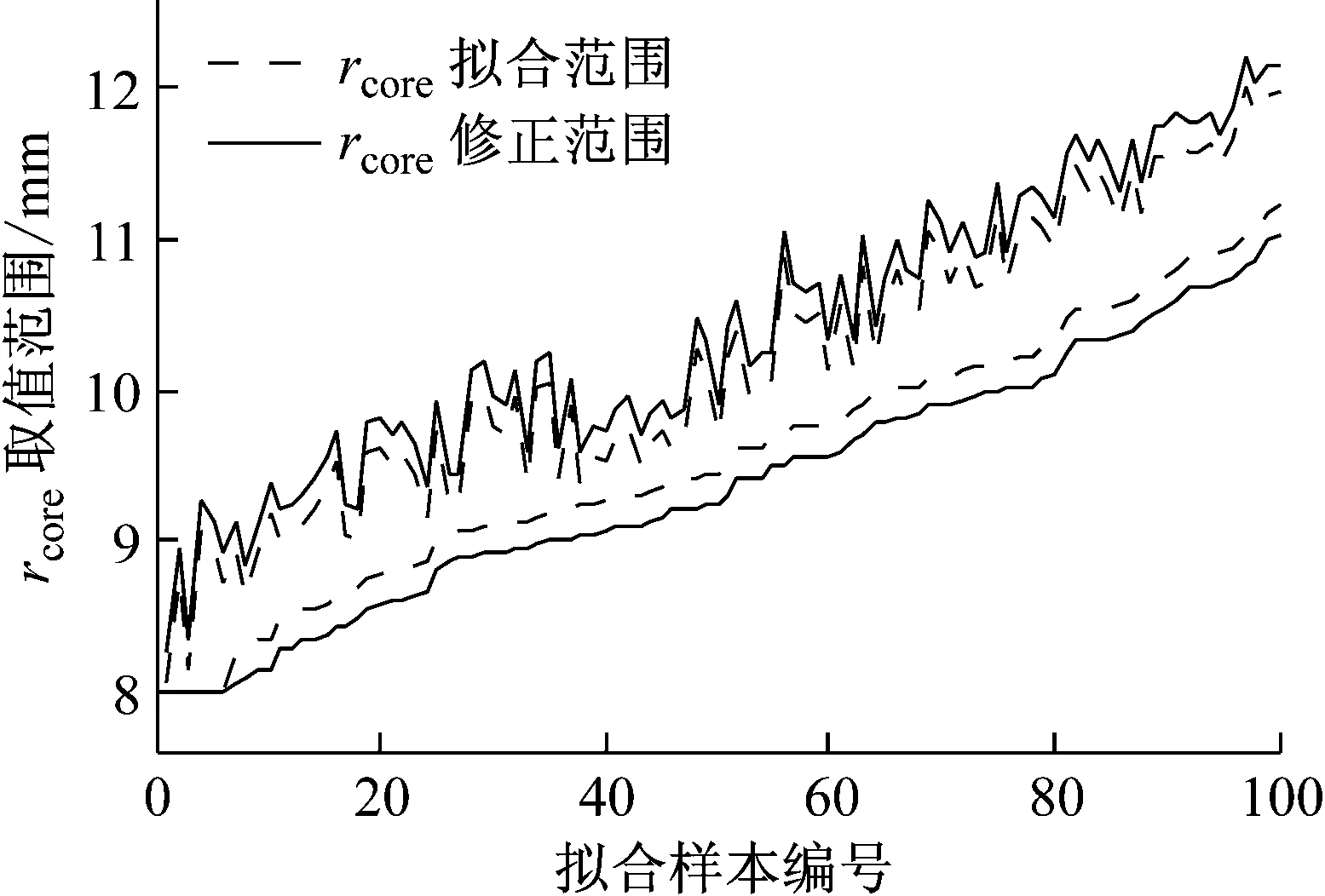
图6 rcore取值范围修正结果
图7所示为某样本剪切应力积分与rcore的关系,可见优化后的rcore设计区间有效避免了左侧区间磁场饱和问题以及右侧非敏感区间,有效缩小了参数优化寻优区间。
3 多参数反馈整车控制算法设计
天棚算法因其简单高效,是目前应用最广泛的半主动悬架控制算法。但传统天棚原理只针对车身运动的部分时段进行阻尼控制,会降低悬架对振动能量的耗散,虽降低了车身加速度,但振动时间和速度加大。
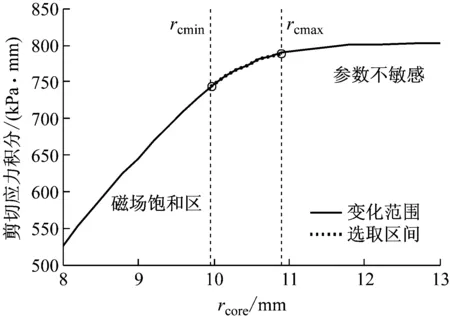
图7 某样本rcore影响效果及约束范围
因此设计基于车身运动状态进行阻尼力分配的整车线性天棚控制算法,并加入基于整车振动能量和弹簧压缩量的反馈修正环节,组成多参数反馈控制算法。算法框图,如图8所示。
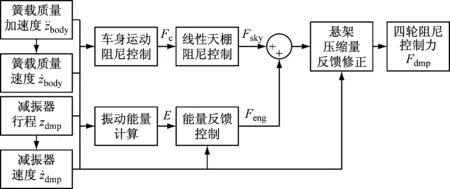
图8 多参数反馈控制算法框图
四轮悬架阻尼控制力Fdmp
Fdam(i)=αz(j)(Fsky(i)+Feng(i))
(19)
式中αzf、αzr为悬架行程修正系数,以降低大行程时车身瞬时加速度;Fsky为线性天棚阻尼力,Feng为能量反馈控制力;i=fl,fr,rl,rr,j=f,r,下同。
αz(j)=
(20)
式中:k1,k2,z1,z2为控制参数;目标车型弹簧与减振器同轴安装,zspr=zdmp,为弹簧压缩量。
线性天棚阻尼力Fsky
Fsky(i)=
(21)
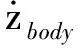
其中Fc为根据车身运动生成的阻尼力
(22)
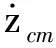
能量反馈控制力Feng
(23)
各悬架振动能量E定义为
(24)
式中:k为各悬架簧载质量占比。
车身振动能量Ebody表示为
(25)
式中:Jp为车身俯仰转动惯量;Jr为车身侧倾转动惯量。
所设计的多参数反馈控制算法通过整车仿真进行参数优化。减振器设计目标车型为某自主品牌B级轿车,前置前驱,整备质量1 435 kg,轴距2 740 mm,前后悬架均为独立悬架,前/后悬架弹簧刚度为52 N/mm、33 N/mm,非簧载质量50 kg。
使用Carsim与Simulink搭建控制器在环整车仿真平台,仿真工况为B级路面,70 km/h匀速行驶,以质心位置总加权加速度作为评价指标[14],采用遗传算法优化80代,参数优化结果,如表2所示。
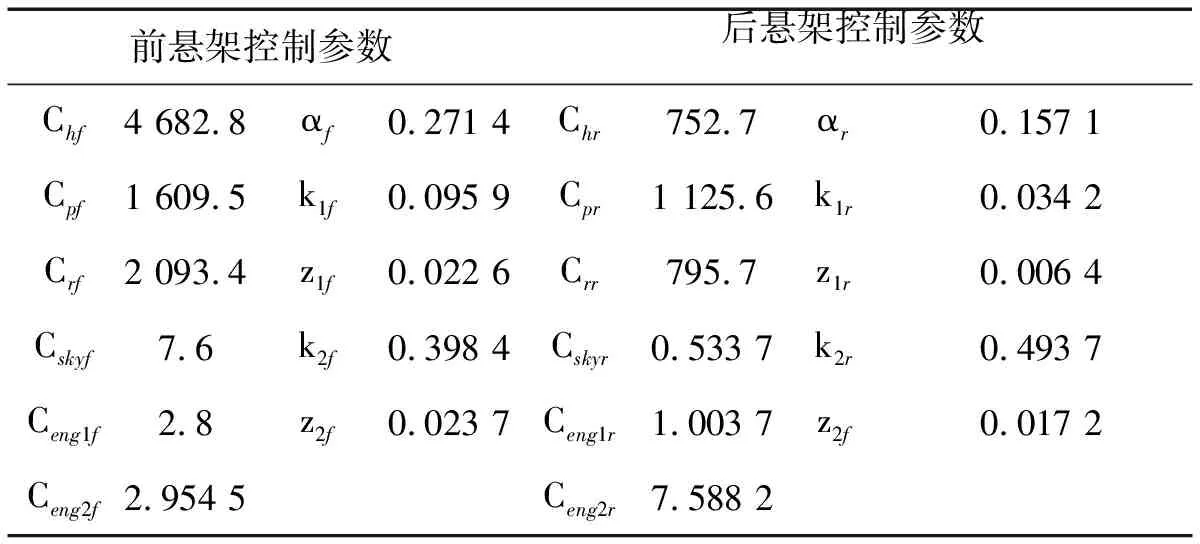
表2 多参数反馈控制参数优化结果
多参数反馈控制与被动悬架、天棚控制算法的性能对比,如表3所示。部分车身振动参数,如图9所示。
结果表明多参数反馈控制下的车身各加权加速度明显低于被动悬架,且较天棚控制算法有一定优势。相比天棚阻尼控制可有效降低车身振动速度与俯仰角。
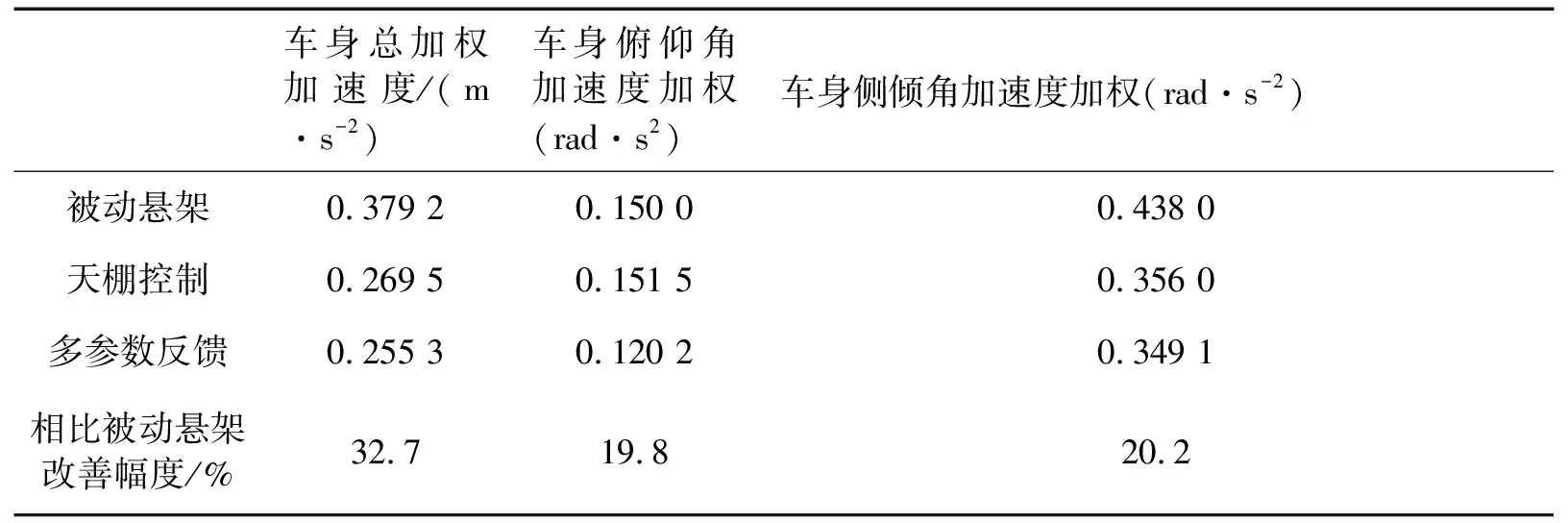
表3 多参数反馈算法控制效果对比

(a) 车身垂直加速度对比(b) 车身垂直速度对比

(c) 俯仰角加速度对比(d) 俯仰角对比
图9 车身振动控制对比
Fig.9 Control effect of body vibration
4 基于整车仿真的减振器参数优化
根据半主动悬架工作机理,搭建包含执行器特性的整车优化仿真平台对前后减振器进行设计参数优化,结构如图10所示。
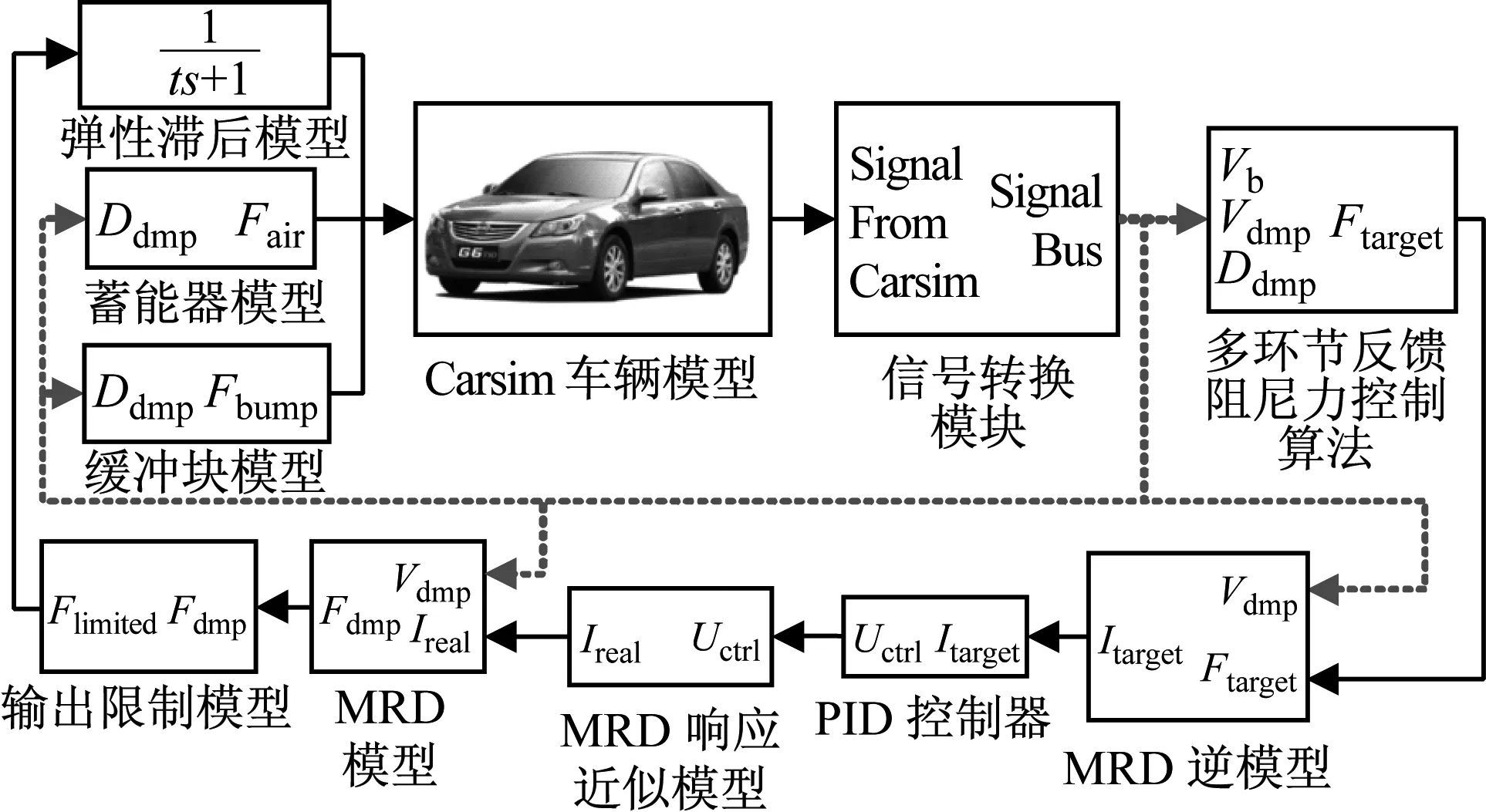
图10 包含执行器特性整车优化仿真平台
仿真平台中采用近似分段直线模型及其逆模型作为MRD模型模拟阻尼力生成及电流控制量计算过程,由式(15)及PID控制算法模拟MRD响应过程,通过式(2)、式(3)计算输出限制范围模拟设计参数下的MRD性能,忽略剪切应力变化对减振器弹性的影响,使用一阶惯性参数模拟MRD结构产生的弹性滞后。
MRD响应模型及弹性滞后模型中的μdmp及时间常数t,通过同缸径MRD试验数据拟合获得,拟合效果,如图11所示。
拟合得到μdmp=0.001 16 H/m,t=0.007。

(a) 电流响应模型拟合效果(b) 弹性滞后拟合效果
图11 减振器响应特性拟合效果
Fig.11 Fitting effect of MRD response features
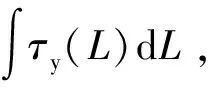
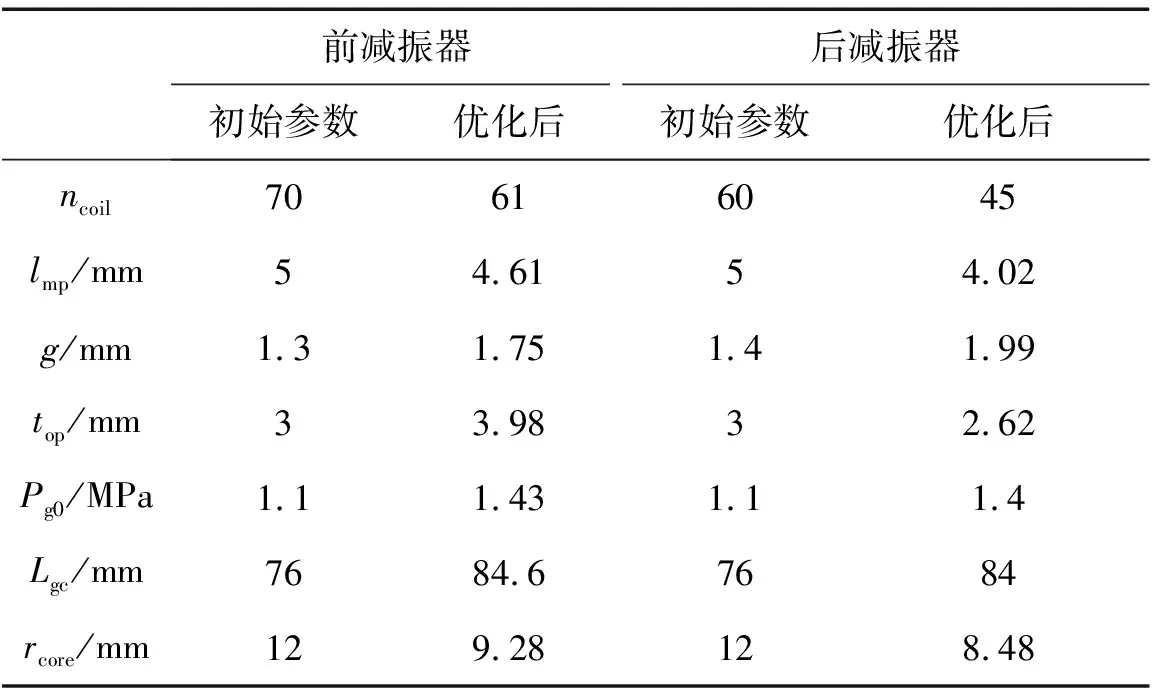
表4 减振器设计参数优化结果
相比初选参数,优化后车身总加权加速度降低了13.1%。前后悬架活塞长度分别缩短了7.62 mm和10.36 mm,有效增大了减振器行程。各减振器工作范围,如图13所示。通过对比可知,优化后的减振器能更好的符合控制算法所需阻尼力范围,从而达到更好的控制效果。
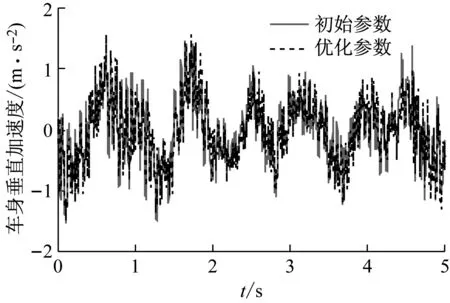
图12 优化前后车身垂直加速度对比

(a) 初始参数前减振器(b) 初始参数后减振器

(c) 优化参数前减振器(d) 优化参数后减振器
图13 优化前后减振器工作范围对比
Fig.13 Working range of MRD before and after optimization
5 结 论
本文通过对车用MRD进行动力学、几何、响应特性等多个方面建模及约束分析,筛选出核心设计参数。创建磁场重要参数rcore动态约束条件并使用神经网络对参数边界进行拟合。设计多参数反馈整车控制算法并使用遗传算法进行参数优化,搭建整车及执行器响应模型联合仿真平台,以车身总加权加速度为指标进行了减振器参数全局优化。
仿真结果表明:通过神经网络模型计算并修正后的设计区间有效缩小了rcore的优化范围,有效避免了磁场饱和问题并避开了不灵敏区间;设计的多参数反馈控制算法有效改善了平顺性,相比天棚控制算法有效降低了车身垂直速度和俯仰角;基于整车在环仿真遗传优化获得的减振器相比初选设计更好的满足了阻尼力控制需求,改善了车辆平顺性。
