基于变分模态分解与流形学习的滚动轴承故障特征提取方法

戚晓利， 叶绪丹， 蔡江林, 郑近德， 潘紫微， 张兴权

(安徽工业大学 机械工程学院， 安徽 马鞍山 243032)

由于机械设备振动信号大部分是非平稳、非线性信号，因此机械设备故障诊断的关键是如何从非平稳、非线性信号中提取故障特征信息[1]。近年来，许多非线性动力学理论如经验模态分解(Empirical Mode Decomposition, EMD)和局部均值分解(Local Mean Decomposition, LMD)方法已被广泛应用于机械设备故障诊断中，并在研究领域取得了丰硕的成果。如Zhu等[2]根据计算EMD分解所得到的故障高频分量与正常状态信号的频域相关系数，通过观察绘制的相关系数曲线的走势，来检测轴承的早期故障。张淑清等[3]将EMD和Duffing振子相结合应用于小电流系统故障中，对故障零序电流进行EMD分解处理后，输入到Duffing振子中，通过观察系统相图变化来确定当前线路是否发生故障。虽然EMD方法受到机械故障诊断领域相关学者的关注，并成功应用于滚动轴承故障特征提取中，但其分解存在端点效应、易出现模态混叠以及分解误差大等问题。

针对这些问题，有些学者做了进一步的研究，如陈亚农[4]等应用LMD方法对滚动轴承损伤类故障振动信号进行分解，并对冲击特征明显的PF分量的瞬时幅值进行频谱分析，结果表明该方法不但能够有效判断故障有无，而且能够更大程度上避免误判。Wang[5-6]等对LMD方法和EMD方法进行了比较，研究结果表明，在端点效应、迭代次数、获取信号的瞬时频率准确性等方面，LMD方法均要优于EMD方法。需要指出的是，虽然LMD和EMD这两种方法目前已经成功应用于故障特征提取中，但两者均属于递归模式分解，还是存在端点效应、分解误差大以及对相近频率的信号无法正确分离等问题[7]。

而近几年提出的变分模态分解[8](Variational Mode Decomposition，VMD)是一种新的信号分解估计方法，它摆脱了EMD等方法的递归模态分解框架，根据预设模态分量个数对信号进行分解。与EMD相比具有采样效应小、噪声鲁棒性好，并能将两个频率相近的纯谐波信号成功分离等特点。如An等[9]提出了一种基于能量分布变分模态分解的滚动轴承故障诊断方法，首先用VMD将原始振动信号分解成有限个分量；然后根据最近邻算法从每个分量中提取能量特征参数作为分类器的输入参数值，从而识别出风力发电机中的滚动轴承发生故障的类型。Wang等[10]提出了一种基于VMD的摩擦故障诊断方法，利用VMD通过数值模拟响应信号和实际振动信号，检测转子故障诊断中多次摩擦引起的特征，通过对比分析经验小波变换(Experience Wavelet Transform, EWT)，EEMD和EMD方法，得出其诊断效果更好。刘长良等提出了基于VMD和奇异值分解的特征提取方法，并采用标准模糊C均值聚类进行故障识别，通过对同一负荷以及变负荷下的故障信号进行分析处理，得出该方法能精确、稳定的提取故障特征，为滚动轴承智能故障诊断提供了参考。马增强等[11]提出了基于VMD和能量算子的滚动轴承故障特征提取方法，该方法提高了信号的分解效率，降低了噪声的影响，能够实现滚动轴承故障的精确诊断。目前，VMD方法已被应用于机械设备故障领域，丰富了机械设备故障诊断的技术和手段。

由于在实际采集信号时，通常需要通过各种监测传感器获取大量的状态信息数据，这使得轴承状态数据维数大幅度提高，导致维数灾难出现，不利于分类识别。而数据降维方法具有良好的维数约简能力。该方法是从复杂、高维的观测数据中，高效快速的挖掘出隐藏在运行数据中有效的低维结构，其目的是实现特征提取和故障诊断。目前已有的数据降维可分为两类：① 线性数据降维方法; ② 非线性数据降维方法。主成分分析(Principal Component Analysis，PCA)是典型的线性数据降维方法，具有许多优点，如计算简单、对具有线性结构的高维数据能取得较好的低维映射结果。但在实际中，获取的高维观测数据多数具有非线性特征，采用上述的线性数据降维方法很难真实、准确反映高维数据的内在本质结构以及数据之间的相关性。针对高维数据的非线性特点，近年来发展了非线性降维方法。应用最多的是基于流形的方法，主要包括局部保留投影算(Locality Preserving Projection，LPP)、局部线性嵌入方法(Locally Linear Embedding，LLE)、等距映射方法(Isometric Mapping，ISOMAP)、拉普拉斯特征映射法(Laplacian Eigenmap，LE)和局部切空间排列方法(Local Tangent Space Alignment，LTSA)等。目前，有不少学者将流形学习法应用于高维非线性故障样本的学习，可有效发现数据的内在本质特征，为故障诊断提供了新的途径[12]。如王斐等[13]将局部特征尺度分解和流形学习算法局部切空间排列相结合，应用于滚动轴承故障诊断中，发现所提出的方法能够准确提取滚动轴承内圈和外圈故障信号的特征频率。向丹等[14]提出了将EMD、样本熵和LLTSA(Linear LTSA)相结合的轴承故障诊断方法，实验分析证明该方法在降低特征数据复杂度的同时，增强了故障模式识别的分类性能。苏祖强等[15]提出特征选择与流形学习相结合的故障诊断方法，在提取特征向量后，利用线性局部切空间排列算法进行降维，最后进行模式识别，结果表明，该方法的分类效果良好。

基于VMD算法和流形学习的优点及其在机械设备故障诊断领域的成功应用，本文针对圆柱滚子轴承振动信号具有调幅调频特征、反应状态信息的能量特征较为微弱，特征提取困难以及特征量数值区分不明显等特点，提出了一种VMD与LTSA相结合的滚动轴承故障诊断方法，首先将采集的原始信号经VMD分解后，通过求取瞬时频率的均值来确定各阶模态的有效分量，并得到相应的时频域参数特征叠加构造故障样本特征集，再利用LTSA对故障样本特征集进行数据降维处理，提取出其敏感特征，最后将敏感特征输入给K-means分类器中实现滚动轴承的智能故障诊断。

1 基于VMD与LTSA相结合的特征提取

1.1 VMD原理

VMD是一种自适应信号处理新方法，其分解是基于经典维纳滤波、希尔伯特变换和混频的变分问题求解过程。该算法可分为变分问题的构造和求解。下面对VMD算法变分问题分别进行介绍。

1.1.1 变分问题的构造

假设每个模态是具有中心频率的有限带宽，中心频率和带宽在分解过程中不断更新，VMD分解是寻求K个估计带宽之和最小的模态函数，使得每个模态的估计带宽之和最小，约束条件为各模态之和等于输入信号f，详细构造步骤如下。

步骤1通过Hilbert变换计算得出每个模态的解析信号，其目的是得出单边频谱

(1)

式中：uk(t)为k个模态函数；δ(t)为脉冲函数。

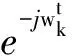
(2)

步骤3求解调信号梯度的二范数并估计每个模态带宽，约束变分问题表达式为

(3)

1.1.2 变分问题的求解

步骤1引入二次惩罚因子α和拉格朗日乘法算子λ(t)，将约束性变分问题转变为非约束性变分问题，其中二次惩罚因子可在高斯噪声情况下保证信号的重构精度，拉格朗日算子使得约束条件保持严格性，增广的Lagrange表达式如下

L({uk},{wk},λ):=

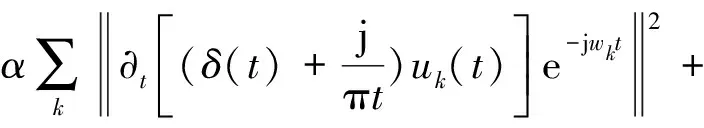
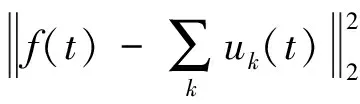
(4)

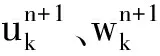
1.2 VMD算法

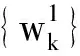
步骤2更新uk和wk；

(5)

(6)

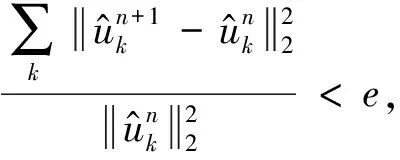
VMD算法可以概括为：① 各模态在频域中不断更新，然后通过FFT逆变换到时域；② 作为各模态的功率谱重心，中心频率被重新估计，并以此循环更新。

1.3 基于LTSA高维特征获取及数据降维

选取轴承振动信号VMD分解的每阶模态的8 个时域统计参数作为时域特征向量，来反映轴承振动信号时域的微弱变化，另外，对采集到的轴承振动信号各阶模态进行 3 层小波包分解，分别求出每个分量的能量值，为了避免元素之间的数值或者数量级存在较大差距时，较小数据被淹没的可能，需对特征量进行归一化处理；表1列出了表征样本的16个时、频域统计参数指标，将上述求得的各模态时域及频域特征向量组合叠加即可构造出滚动轴承振动信号的原始高维特征向量，因本文K值取4，所以得出每段数据长度共提取64个时频域指标。

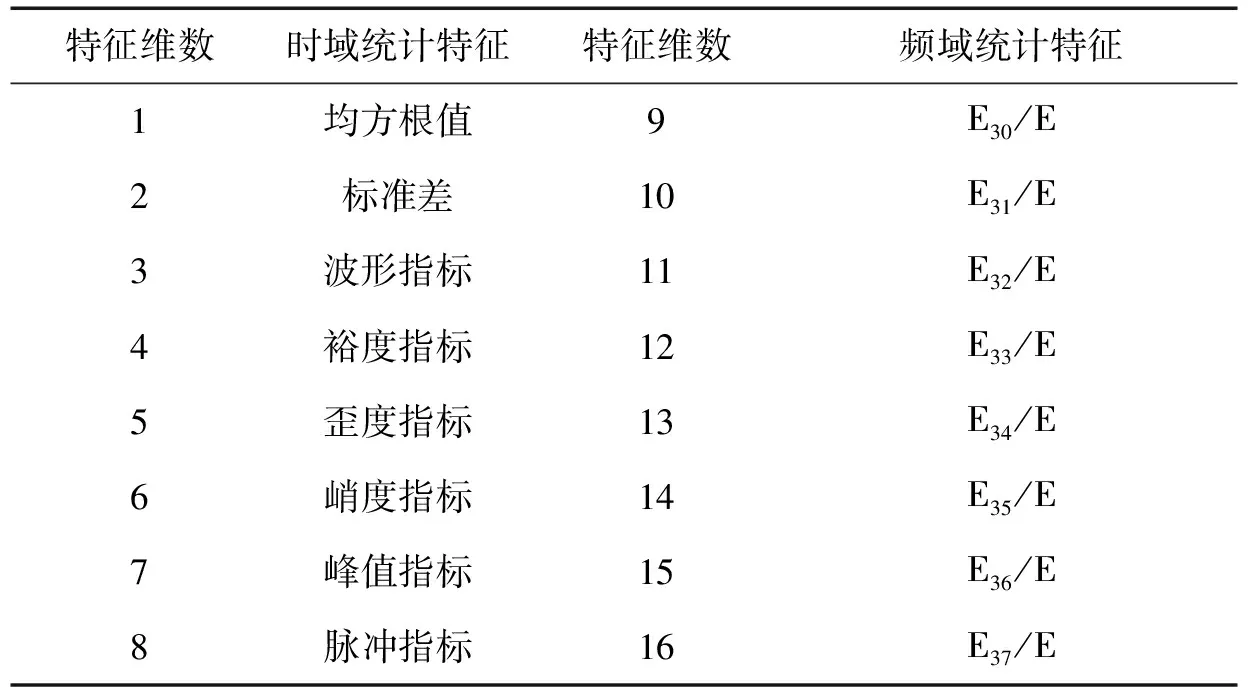
表1 滚动轴承振动信号原始特征向量

然后利用LTSA对敏感特征进行数据降维。LTSA是一种基于切空间的流形学习方法，通过逼近每一个样本点的切空间来构建低维流形的局部几何；然后利用局部切空间排列求出整体低维嵌入坐标。其算法步骤如下。

步骤1选取样本点领域。对每个样本点，按照k-Nearest Neighbor标准，选取样本点xi包括在内的k个最小距离近邻点作为邻域点。将样本点的近邻点组成一个邻域矩阵。

步骤2局部线性投影。计算各样本处d维切空间的正交基和每一个点(j=1,2,…，k)在切空间上的正交投影。

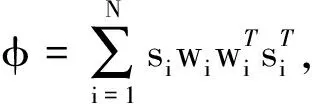
2 K-means聚类算法

K-means聚类算法的概念是Macqueen在1967年提出来的，它是一种最简单地无监督学习方法之一，它可以在没有任何标号的情况下自动发觉簇与簇的中心点。通过不断地对数据对象进行迭代计算聚类中心点，该算法具有简单、高效并且收敛速度很快等特点。算法步骤描述如下。

步骤1设有n个样本X={x1,x2,…,xn}∈Rd构成待聚类数据集，将其划分到K个类别中。随机选取K个样本数据，每个样本数据代表一个初始聚类中心，从而得到初始聚类中心集合C={c1,c2,…,ck}T；

步骤2对剩下的n-K个样本数据，分别计算它们到“步骤1”中每个聚类中心的欧氏距离，然后根据欧氏距离的大小对这n-K个样本数据进行划分，得到具有最小距离的K个类别，用d(xj,ci)表示样本数据xj与聚类中心ci之间的欧氏距离，计算公式如下

(7)

步骤3重新计算K个聚类中心的值，计算公式如下

(8)

式中：i=1,2,…,k；ni是类ci中样本数据的个数；xj代表属于ci类中的样本数据。

步骤4检验聚类操作是否结束，若满足使目标函数式(9)最小或保持不变，则迭代结束，否则重复步骤2、步骤3、步骤4。最小化目标函数公式如下

(9)

式中：Si代表第i个类别中样本的集合。

3 应用实例

3.1 应用对象

为了证明上述方法的有效性，在本文中将该方法运用到实验数据中进行验证，实验选用圆柱滚子轴承(型号4210)为研究对象，其轴承结构参数，如表2所示。

表2 轴承结构参数

表2中：n为滚动体数目；d为滚动体直径；D为轴承节径；α为轴承压力角。

实验采用 SG 双色金属刻字机对圆柱滚子轴承进行加工，来模拟轴承滚动体故障 、内圈故障、以及滚动体与内圈复合的早期点蚀故障。如图1～图3所示。

图1 滚动体和内圈混合故障

图2 滚动体故障

图3 内圈故障

根据轴承参数选用BVT -5系列的轴承振动测量仪进行故障实验，实验现场图，如图4所示。在实验过程中，分别对圆柱滚子轴承进行径向与轴向加载，采用加速度传感器测振动信号，采样频率fs设置为5 120 Hz，传感器位置布置，如图5所示。

在主轴转速为1 800 r/min时，利用加速度传感器分别对轴承正常、滚动体故障、内圈故障以及滚动体与内圈复合故障等4种运行状态进行振动信号采集，4种运行状态下的振动信号时域波形，如图6所示。

从图6可知，圆柱滚子轴承4种运行状态均出现了明显的冲击分量，因为时域分析法对轴承局部故障比较敏感，并且该方法易受噪声影响，所以通过振动波形很难识别滚动轴承的运行状态。本文以圆柱滚子轴承内圈故障振动信号为例，对其先进行VMD分解，得到相应的时频域参数特征叠加构造故障样本特征集，再利用LTSA对故障样本特征集进行数据降维处理，提取出其敏感特征，最后将敏感特征输入给K-means分类器中实现滚动轴承的智能故障诊断。

图4 实验现场图

图5 传感器位置布置图

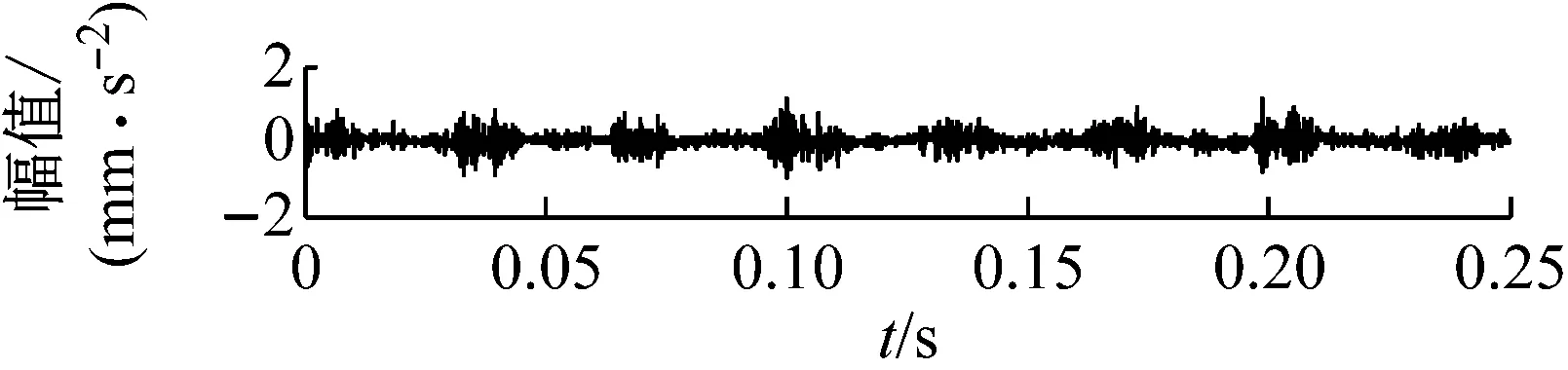
(a) 滚动体故障

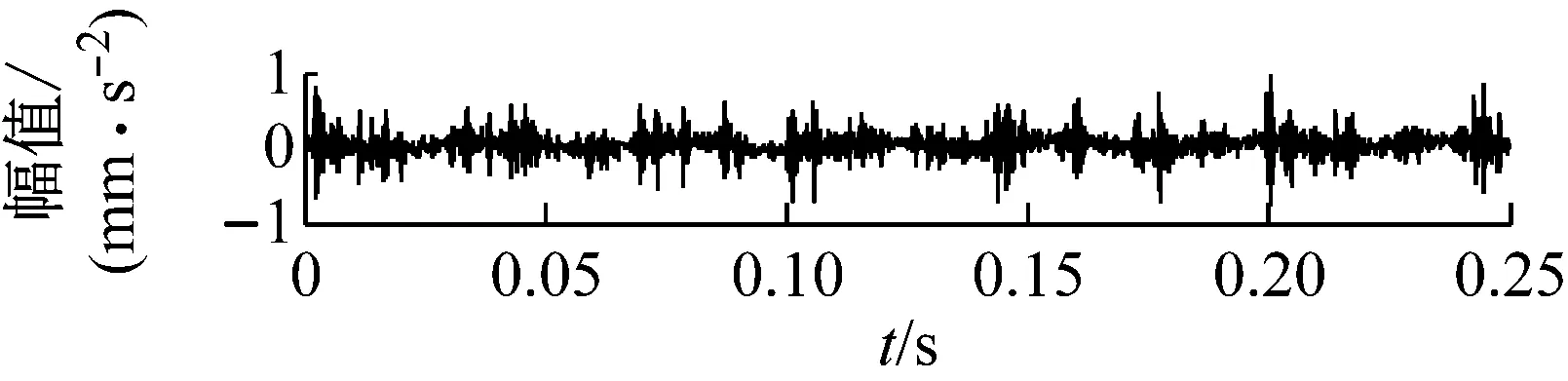
(b) 复合故障

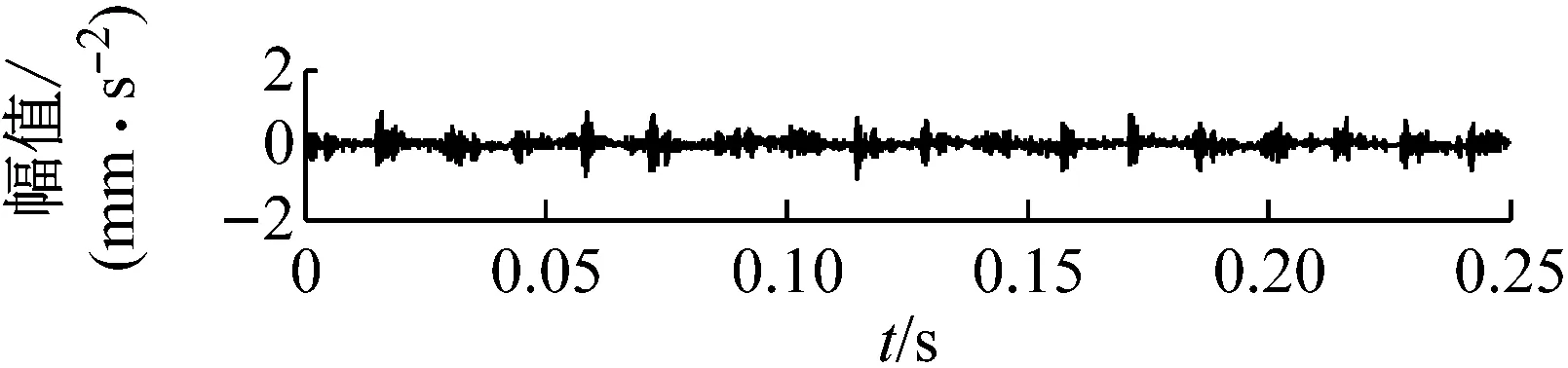
(c) 内圈故障

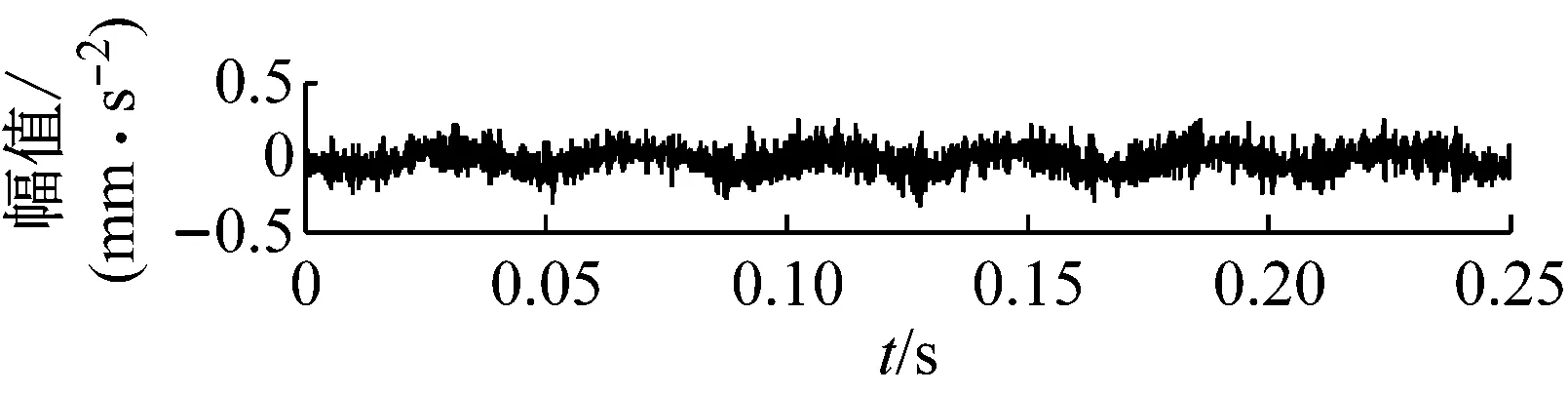
(d) 正常信号

需要注意的是，在运用VMD算法时，模态数K的准确预估决定了VMD能否从原始振动信号中精确分解出较高的分量，本文是通过分析VMD分量K取值从1～9情况下求取瞬时频率的均值并绘制特征曲线来预判K值的。如图7可知，模态数前4个无明显断续现象，而当K=5时，分量会出现断续、下弯现象，因此本文选择前四个分量作为下一步分析的基础，然后对每个分量进行希尔伯特-黄变换，得出VMD分解图和希尔伯特谱，如图8、图9所示。

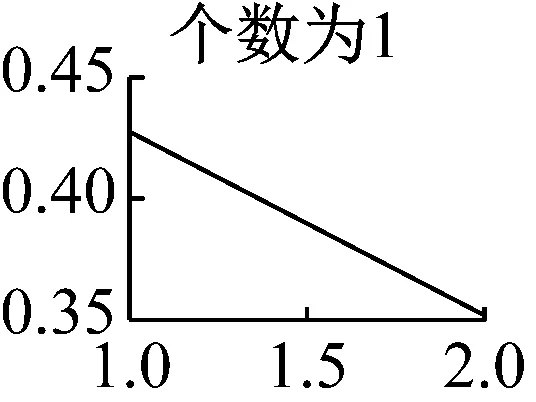
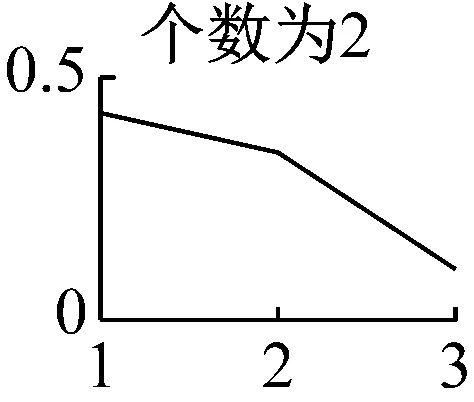
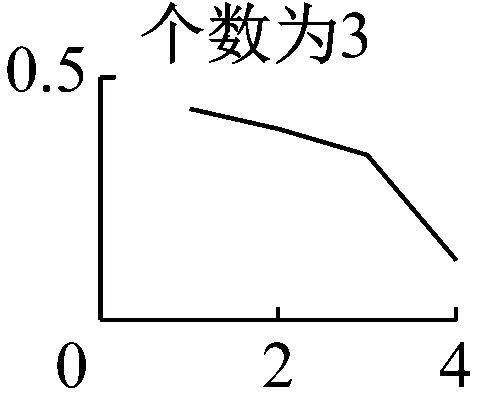
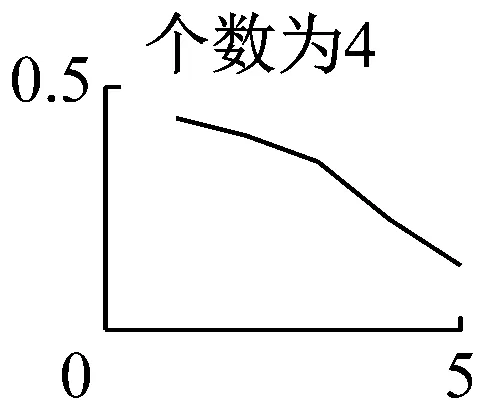
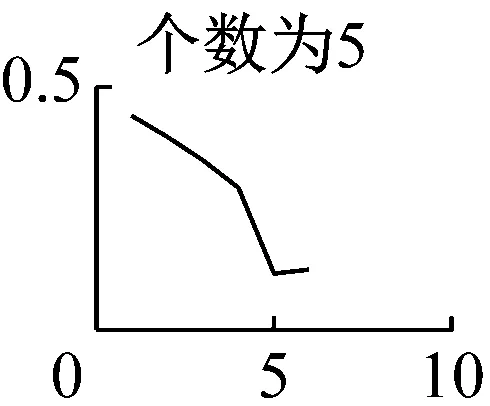
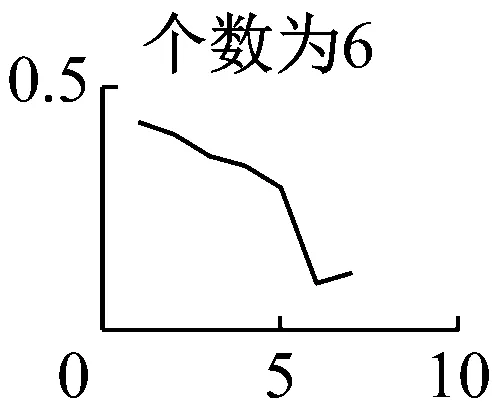
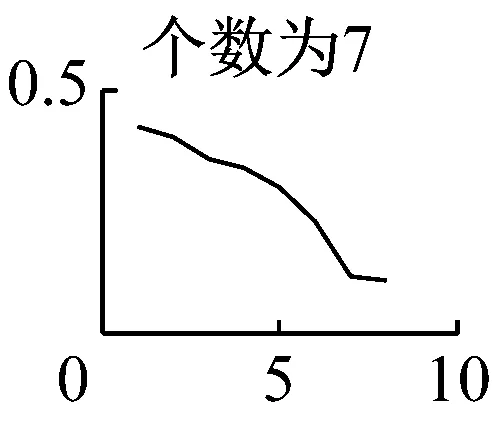
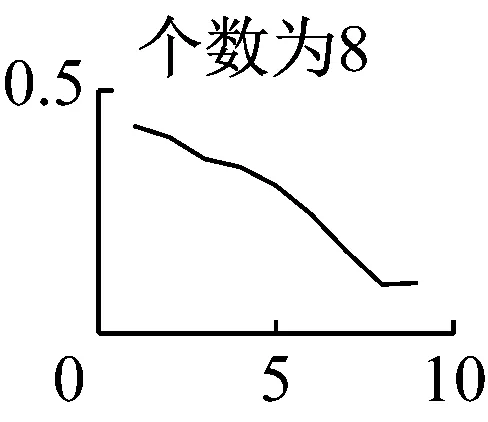
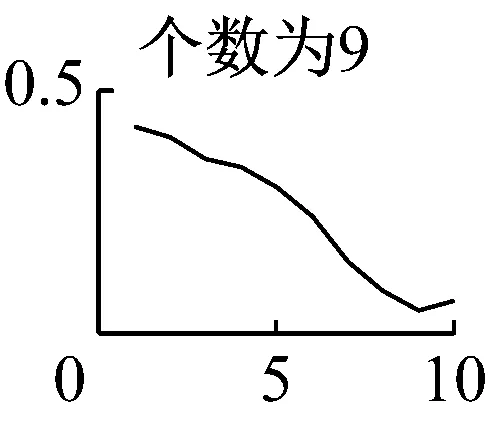
图7 K值1～9时的平均瞬时频率特征曲线

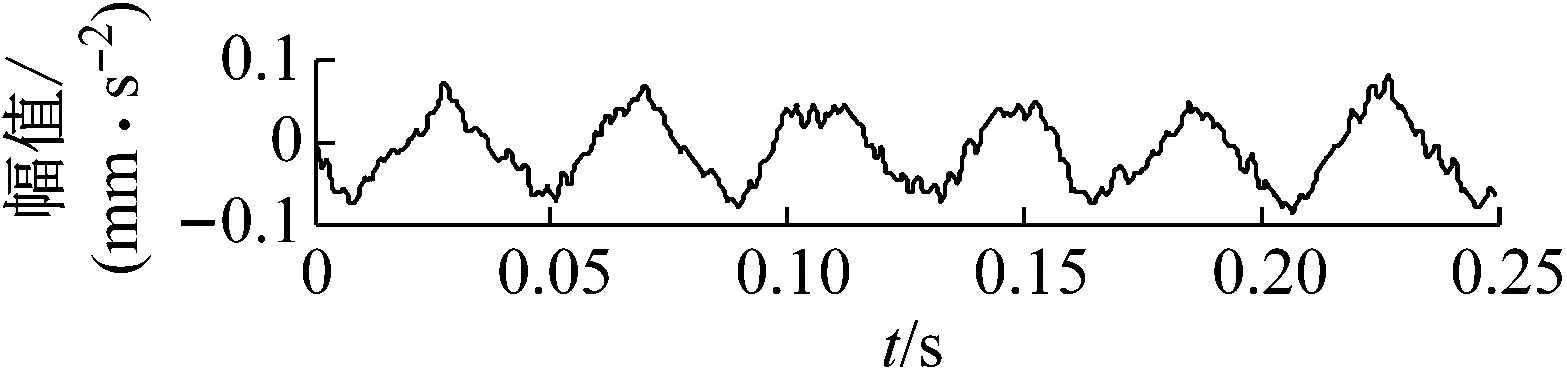
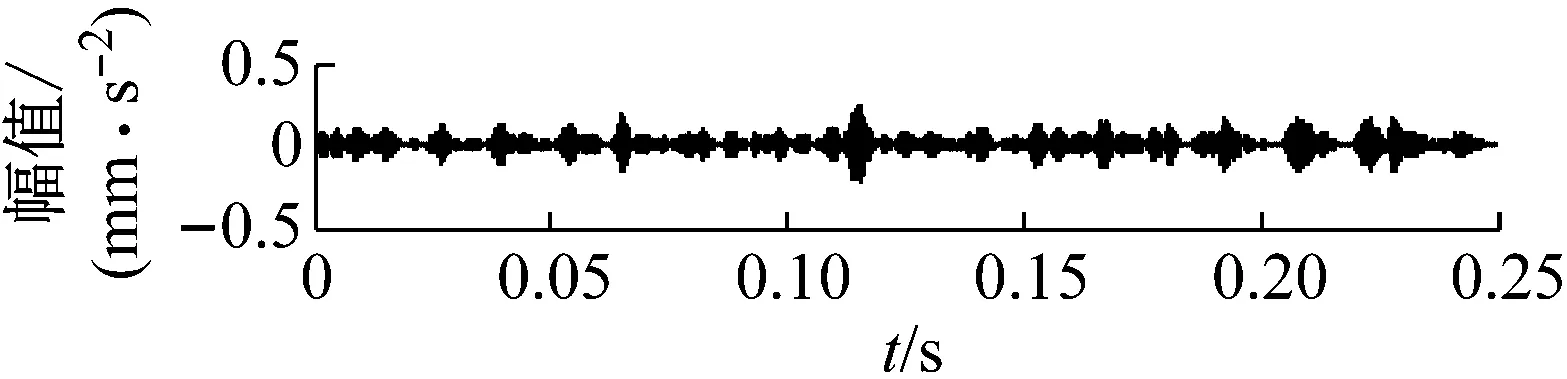
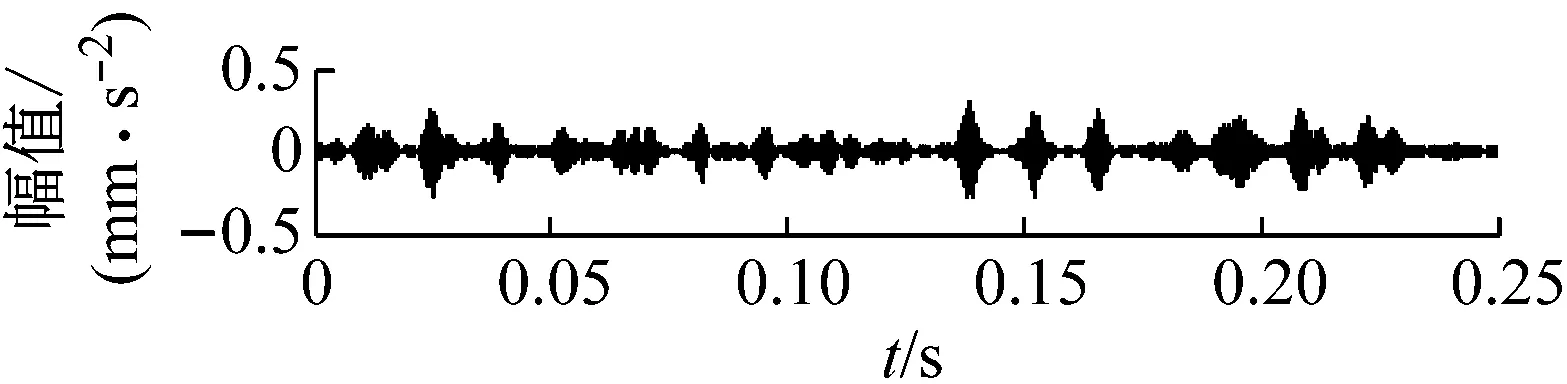
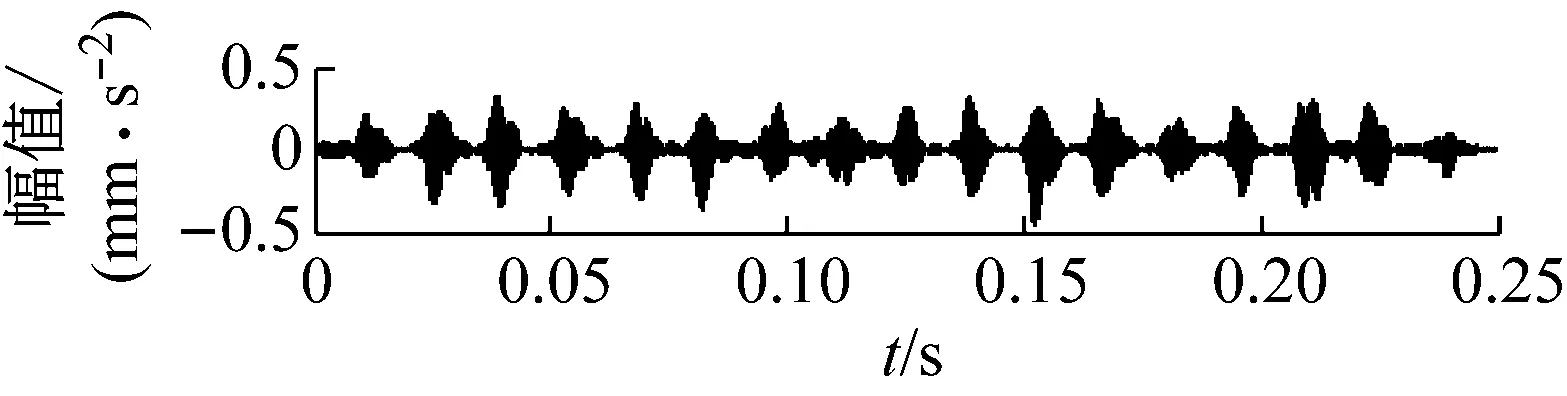
图8 圆柱滚子轴承内圈故障VMD分解结果图

根据圆柱滚子轴承的结构参数，可以计算出内圈故障特征频率为408 Hz，从图9可知，在内圈故障信号的希尔伯特谱图中模态分量2没有明确的谱峰，第1模态分量中533 Hz、812 Hz和第4模态分量808 Hz附近有较为明显的谱峰，其中812 Hz与内圈故障频率(816 Hz)二倍频相近，但仍不准确。第三个分量谱中谱峰423 Hz与内圈故障特征频率408 Hz虽然相近，但谱峰不明显且没有相应的倍频出现。因此无法判断出圆柱滚子轴承出现了内圈故障。综合以上分析，本文对圆柱滚子轴承振动数据进行进一步特征提取是很有必要的。

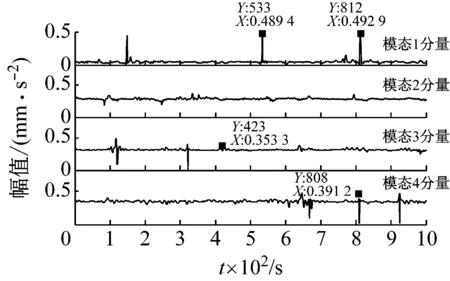
图9 圆柱滚子轴承内圈故障希尔伯特频谱图

3.2 特征提取与识别分析

从采集到的圆柱滚子轴承振动信号中提取正常、滚动体故障、内圈故障、混合故障这4种运行状态各30组样本，数据采样点数均为3 000个，共计120组样本实验数据，用本文方法对该120组样本振动信号进行处理。首先根据求取瞬时频率均值特征曲线预先设置模态数K=4，α采用VMD默认值2 000；τ选为0.3确保实际信号不出现失真现象。接着，选择经VMD分解的前四个分量进一步求得时域指标和小波包频带分解能量所构成的频域指标组成原始特征空间，初步提取高维数据，得到特征空间为R120×64。然后利用流形学习中典型的LTSA算法对高维数据进行二次特征提取得到特征空间为R120×3，将降维后的特征向量输入K-means分类器中识别出故障。为了验证本文所提方法的有效性，将120组样本数据不经任何预处理直接求取时频域特征得到特征空间为R120×16，以及对样本数据分别进行EMD和VMD分解后对各IMF求其时频域特征得高维特征空间为R120×64，再将这三种方法得出的高维特征空间同样进行LTSA降维，得到特征空间为R120×3，并采用相同K-means分类器进行分类，对比效果图，如图10、图11、图12所示。

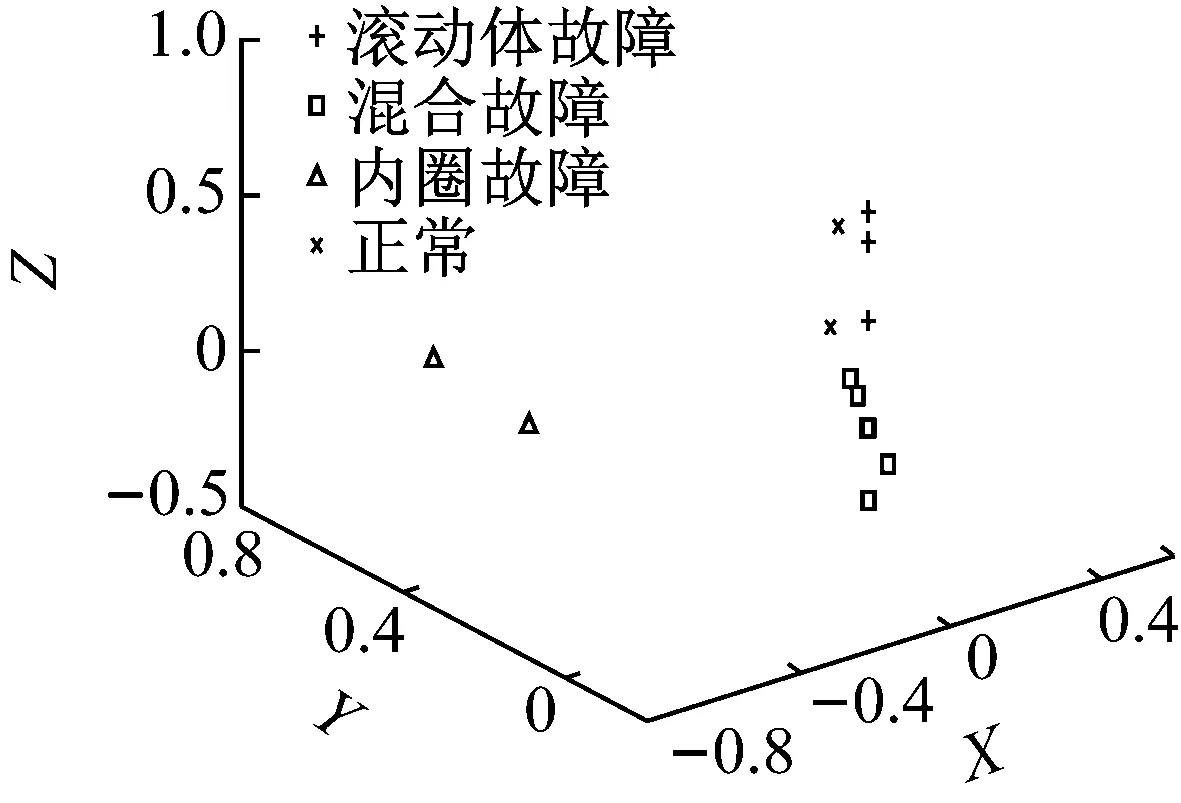
图10 原始特征量+LTSA方法分类图

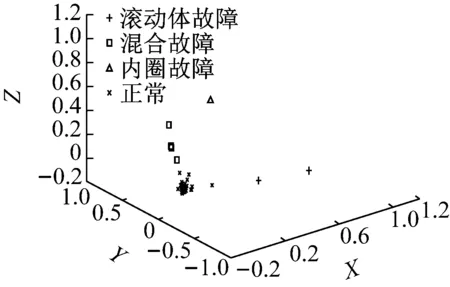
图11 EMD+LTSA方法分类图

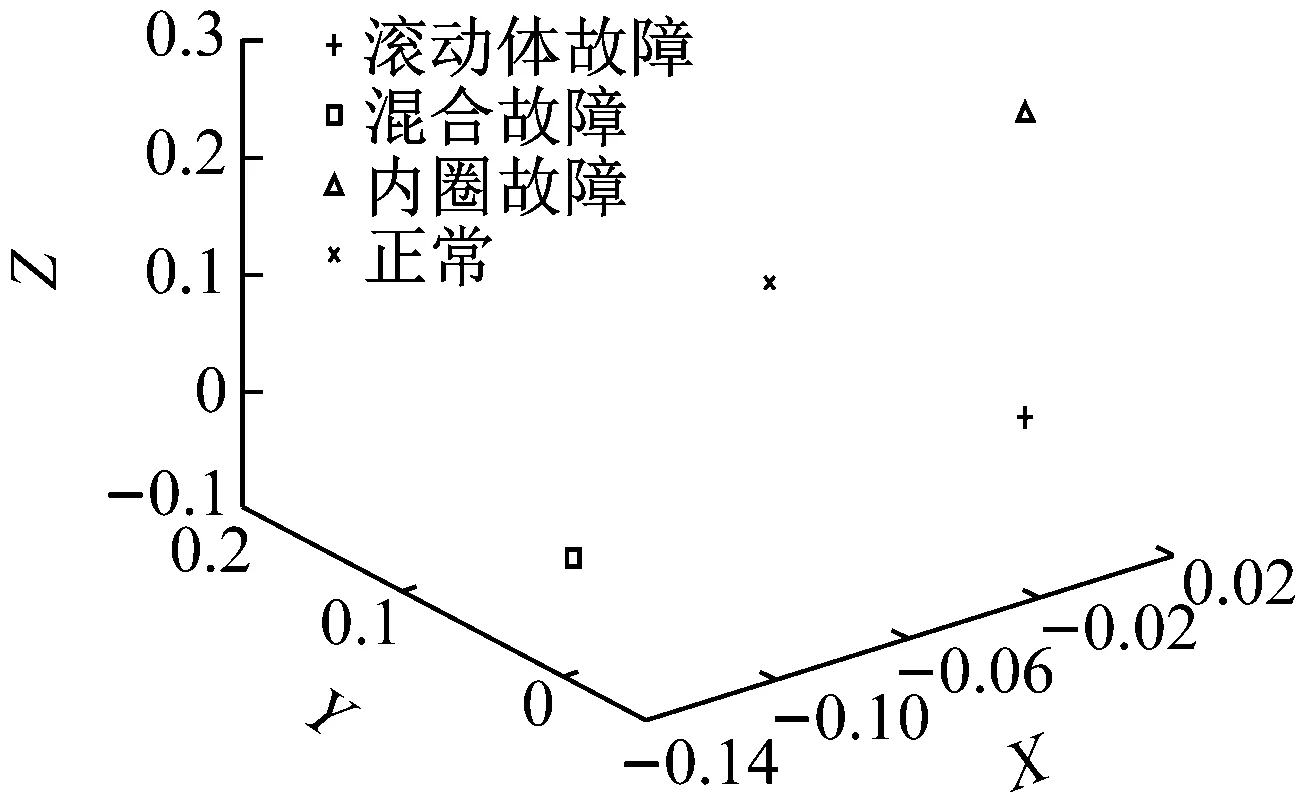
图12 VMD+LTSA方法分类图

从图10(不经过任何预处理,而直接求取时频域特征振动信号得到的分类图)可知，除了内圈故障外，轴承正常、滚动体故障及混合故障这三种情况均出现了类间距较小的情况，故障易混叠，容易发生误判。

从图11可知，基于经验模态分解(EMD)与局部切空间算法(LTSA)相结合的故障诊断方法能够将圆柱滚子轴承正常、滚动体故障、内圈故障及混合故障这四种状态基本分离出来，其中内圈以及滚动体故障在特征空间有较好的聚集度，但混合故障和正常状态时分离效果并不是很好，在一定的数据范围内有一部分样本十分接近，容易发生混叠，从而影响轴承故障的判断。

从图12可知，相比较前两种方法，基于VMD与LTSA相结合的故障诊断方法能够将圆柱滚子轴承正常、滚动体故障、内圈故障及混合故障这四种状态完全分离出来，在故障分类结果图中表现为同种状态30个样本的低维嵌入近似为一点，并且类内散度与类间距均达到最佳效果。

以上定性地对比分析了时频统计量LTSA方法、EMD+LTSA方法和VMD+LTSA方法的故障聚类效果，为了更好地定量对比3种方法的分类效果，本文分别计算了不同运行状态轴承样本在三维子空间的类内距，如表3所示。

表3 不同方法提取的样本类内距统计结果

由表3可知，在3种方法中，时频统计量LTSA方法的聚类效果最差， EMD+LTSA方法次之，其中内圈、滚动体故障和正常状态的类内距比LTSA方法均有明显的下降。VMD+LTSA方法的聚类效果最好，样本类内距明显小于其他2种方法。这表明基于VMD+LTSA的轴承故障诊断方所提取的故障特征最优、聚类质量最好。

3.3 多种数据降维方法对比

由于不同的数据降维方法针对不同数据的特征提取效果不一样，作为比较，本文应用典型的非线性流形学习方法LTSA与线性降维方法PCA，以非线性流形学习方法LPP、LE、ISOMAP、LLE等对初步提取的故障样本高维数据进行降维，其中LTSA算法取数据集样本点的邻域k=6和特征维数d=3；与LTSA流形学习方法形成对比，设定LPP、LE、ISOMAP、LLE算法的投影维数d=3，近邻点数设置为默认值k=12；然后将其分别输入到K-means分类器中进行分类，聚类效果如图13所示。

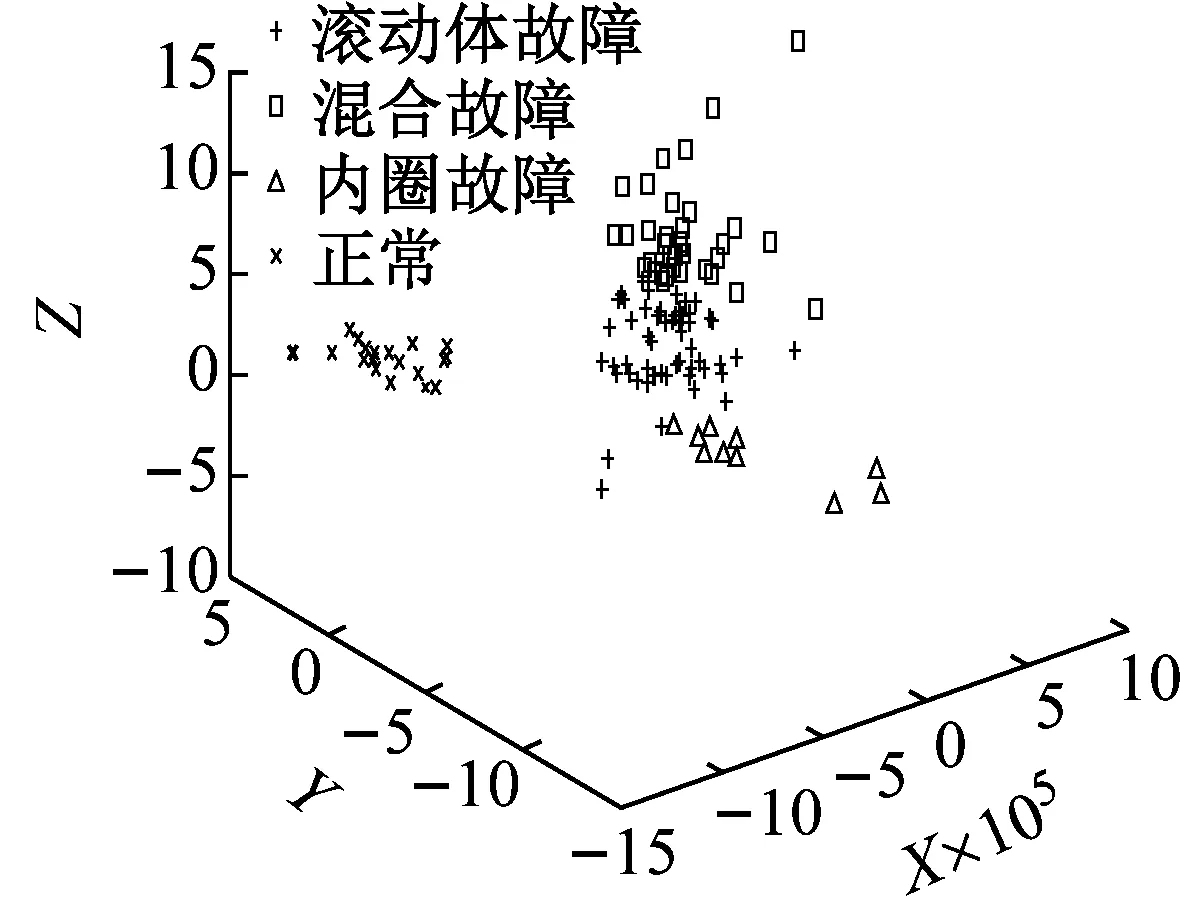
(a) 主成分分析法PCA

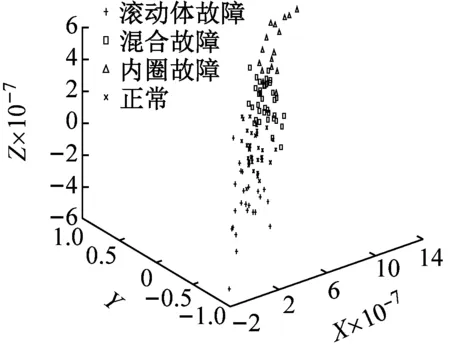
(b) 局部保留投影算法LPP

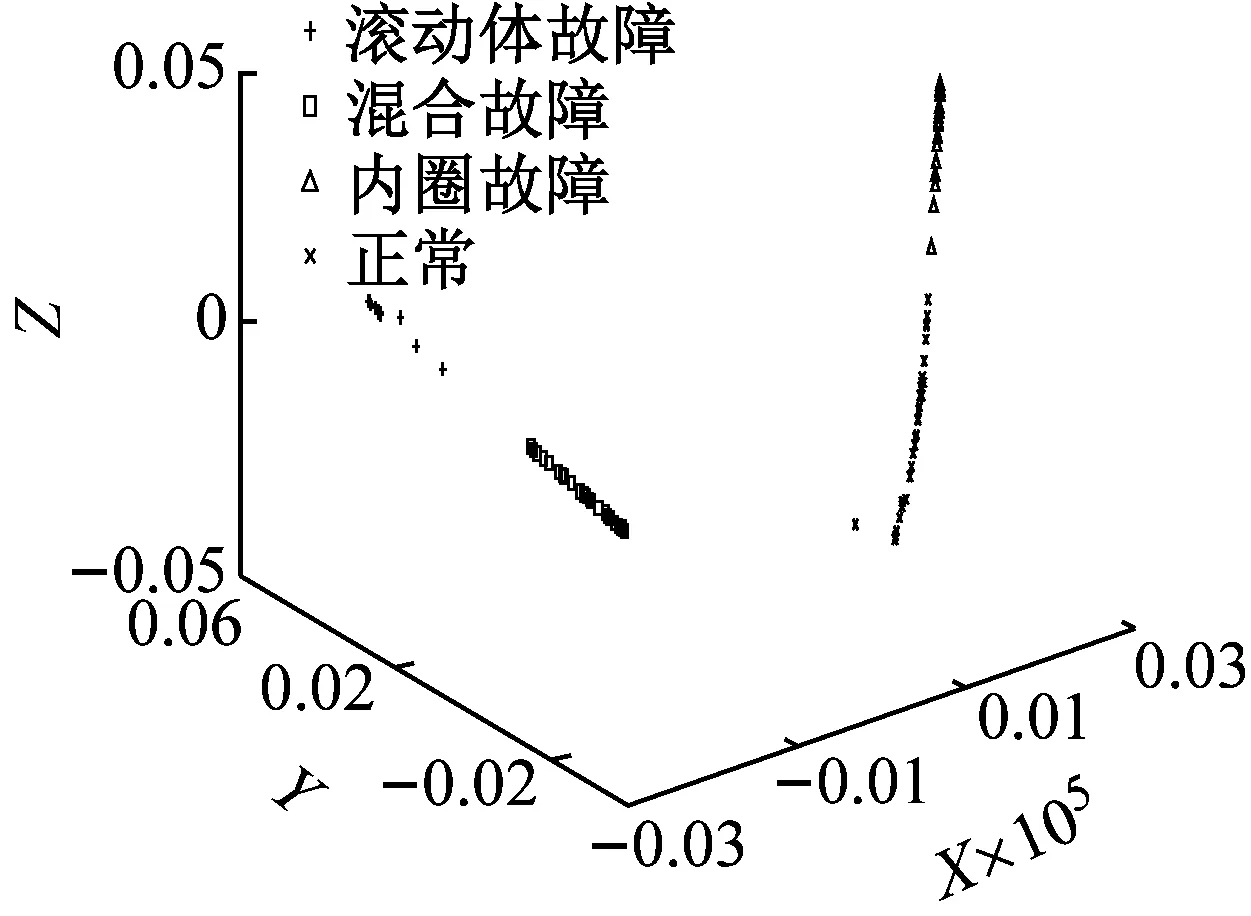
(c) 拉普拉斯特征映射法LE

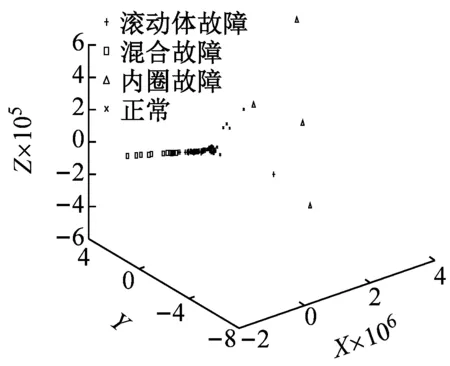
(d) 等距映射方法 ISOMAP

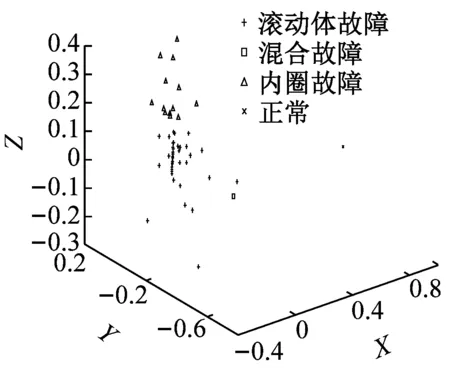
(e) 局部线性嵌入方法LLE

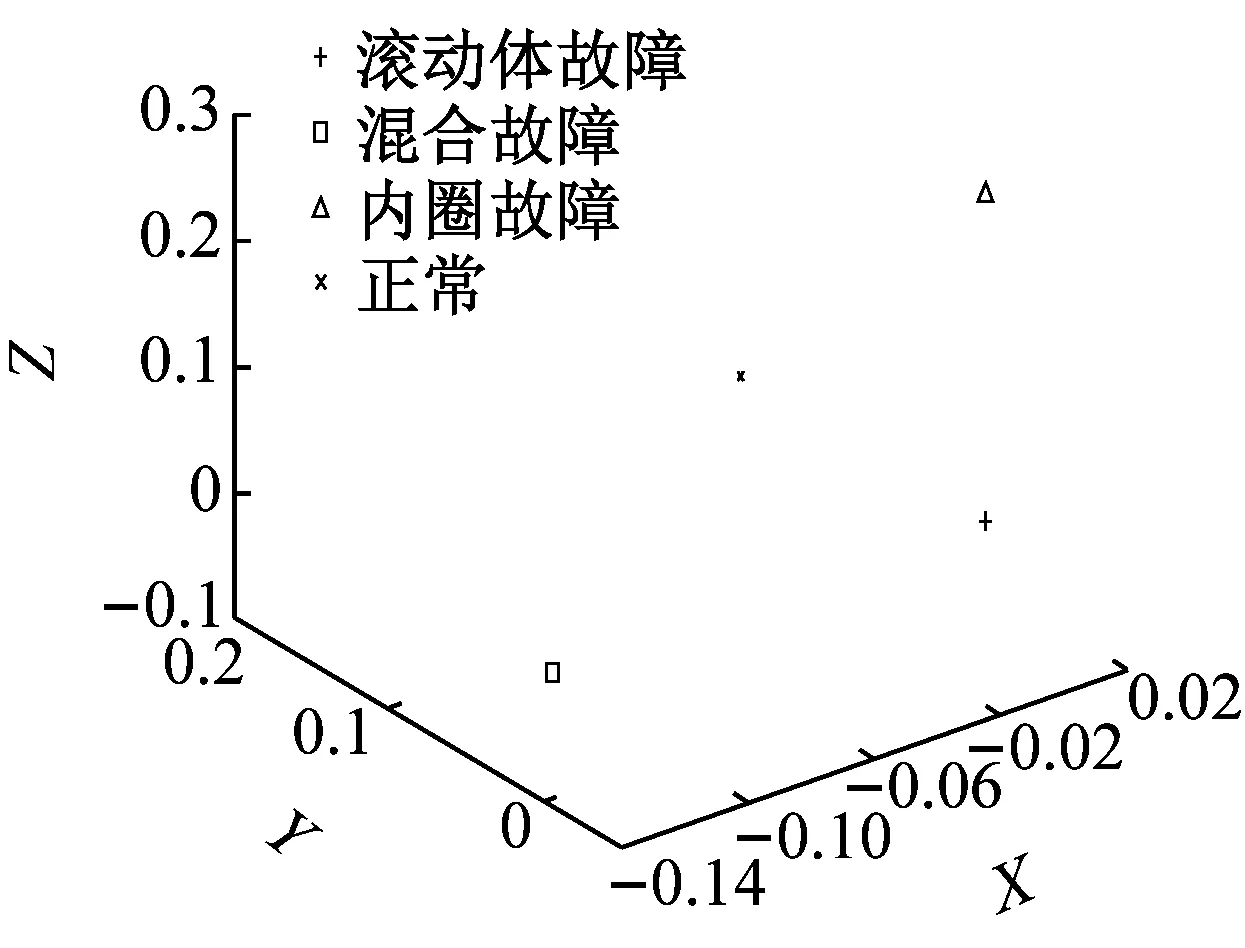
(f) 局部切空间排列方法LTSA

从图13(a)PCA方法和图13(b)LPP方法效果对比图可知，将这两种方法应用于故障样本高维特征数据降维后，都发生了严重混叠现象，但理论上，LPP算法优于PCA算法，在数据处理过程中能够保持数据样本局部流形结构不变。

图13(c)采用了LE方法进行数据降维，四种轴承状态的样本点数据分布较为分散，但能够基本分离，需要注意的是，正常和内圈故障中有一部分样本数据相隔较近，容易发生混叠现象。

图13(d)中采用ISOMAP方法进行降维，除了内圈故障聚类性较好，其余故障均混叠明显，聚类效果不佳。

图13(e)为应用LLE方法降维后的聚类效果图，从图中可以看出，正常和混合故障的样本聚类性较好，易于识别，而其他两种故障发生了混叠，特别是滚动体故障分布离散，识别率低。

图13(f)利用非线性数据降维方法中基于流形的典型方法LTSA对提取的高维数据进行了降维，对于四种轴承运行状态，均呈现了良好的聚类性，便于区分各类故障。

综上所示，流形学习作为一种非线性数据降维方法，其降维效果优于传统的线性降维方法PCA。而在多种流形学习算法中，LTSA与其他4种方法相比更加适用于圆柱滚子轴承故障诊断。

4 结 论

针对圆柱滚子轴承振动信号具有调幅调频特征、反应状态信息的能量特征较为微弱，特征提取困难以及特征量数值区分不明显等特点，提出了一种基于变分模态分解(VMD)和局部切空间排列算法(LTSA)相结合的滚动轴承故障诊断方法。首先将采集的原始信号经VMD分解后，通过求取各阶模态的有效分量，并得到相应的时频域参数特征叠加构造故障样本特征集，再利用LTSA对故障样本特征集进行数据降维处理，提取出其敏感特征，最后将敏感特征输入到K-means分类器中实现滚动轴承的智能故障诊断。实验表明应用该方法进行圆柱滚子轴承故障诊断是切实可行的。本文得出的主要结论如下：

(1) 采用VMD分解时，诊断精度受K值影响较大，本文通过绘制K值的瞬时频率均值曲线来对模态K值进行预估。提出了一种基于VMD和LTSA相结合的故障诊断方法， 并与时频域特征+LTSA、EMD+LTSA 特征提取效果进行了对比分析，发现VMD+LTSA方法要明显优于前两种方法，各类样本均有效识别。从上述圆柱滚子轴承实测信号分析结果来看，预估K值方法和本文所提方法是有效可行的。

(2) 由于不同的数据降维方法的特征提取效果不一样，所以本文将LTSA的维数约简效果与线性降维方法PCA和非线性流形学习方法LPP、LE、ISOMAP、LLE进行对比，结果表明LTSA算法成功提取出圆柱滚子轴承高维非线性数据的低维流形的特征，并且其分类效果明显优于LPP、LE、ISOMAP、LLE等方法，大大地提高了故障识别的精度。