基于风压谱和Hermite模型的大跨干煤棚风压场数值模拟研究
2018-12-21黄铭枫孙轩涛楼文娟胡德军
黄铭枫, 孙轩涛, 冯 鹤, 楼文娟, 胡德军
(1. 浙江大学 结构工程研究所, 杭州 310058; 2. 浙江耀厦控股集团有限公司, 杭州 310011)
风荷载是控制结构安全的重要荷载,特别是对于大跨和高层结构,风荷载及其动力效应常常成为设计的主导因素。研究表明在屋面结构的来流前缘、后部尾流区及角区附近,风荷载常常表现出强烈的脉动和非高斯特性[1]。与高斯过程相比,非高斯随机过程的峰值更大,往往是导致屋面破坏的主要原因,因此对非高斯风荷载的研究具有重要意义。对于干煤棚等大跨建筑,结构的几何非线性程度较高,相比于频域风振分析法,时域法可以考虑结构的非线性因素,能更为精确的获得结构风致动力效应。然而,大跨屋盖结构风洞测压试验得到的风压时程数据往往有限,难以满足结构动力可靠度研究[2]的需要。因此,有必要研究非高斯风压场和风荷载的数值模拟方法[3]。
屋面脉动风压场的特性可由时域统计量,如均值、方差、偏度、峰度等,和频域的脉动风压谱来描述。屋面脉动风压谱的特性十分复杂,不仅受到建筑尺寸、屋盖形状、来流方向及湍流度影响,还与测压系统采样频率密切相关。传统的准定常假定认为,建筑表面风压的脉动与来流风速脉动一致,因此采用来流风谱转换得到建筑表面风压谱。而实际上,大跨屋盖表面的脉动风压主要受特征湍流的影响[4],作用于屋盖的风场与自然来流特性存在较大差别,不适用准定常假定[5],因而有必要引入风压谱模型。Kumar[6]对屋盖表面的风压谱进行研究,得到了风压谱的指数表达形式。孙瑛[7]分析了大跨平屋盖和鞍形屋盖在不同风向角下的风压谱特征,根据风压谱形状和峰值对应频率对屋盖表面进行了分区,并给出了不同区域的三参数风压谱经验表达式。Su等[8]基于115种典型大跨屋盖的风洞试验数据,对三参数风压谱模型进行了改进,并通过风致响应分析验证了该模型在工程实践中的适用性。之后,苏宁等[9]基于不同矢跨比、高跨比的球面屋盖模型风洞试验数据,利用广义回归神经网络预测了屋盖表面风荷载的特征参数。
静态转换法(Static Transformation Methods)是非高斯风压模拟的一种常用方法,即将高斯随机过程通过一定变换关系转化成满足指定功率谱和高阶统计量的非高斯随机过程。李锦华等基于Johnson转换和数字滤波理论,提出了一种能快速生成指定偏度和峰度的非高斯脉动风压的方法。李璟等[10]采用三次多项式将非高斯风压场转换为一个虚拟的多变量高斯过程,并利用谐波合成法生成风压时程样本,该方法能快速模拟非高斯风压场,但对功率谱的模拟效果较差。 Winterstein[11]首次提出利用Hermite多项式将一个高斯过程转换成非高斯过程,但该方法只能用于软响应过程,且对功率谱的模拟不太理想。 Gruley等[12]基于Hermit多项式的谱修正法提出了平稳非高斯风压时程的模拟方法,但该方法模拟得到的单样本的偏度和峰度精度较差,需要多次模拟取平均才能得到较好的结果。之后,Masters等[13]改进了Hermit多项式变换函数,使之在模拟非高斯时程时能更快的收敛到目标值。徐飞等[14]利用实测时程数据的分布函数和Hermit多项式来构造幅值调制信号,并通过与高斯过程相乘调制来得到非高斯时程。此方法不仅可以模拟非平稳过程,而且对于峰度较大的非高斯时程也不会发生失真现象,具有较高的精度。Huang等[15]等也基于Hermit多项式变换,利用TPP方法和Deodatis的谱修正方法[16]进行了非高斯风压时程的模拟。罗俊杰等[17]采用非线性无记忆转换法模拟多点非高斯过程,并提出了分解谱密度函数修正法,以保证功率谱密度函数矩阵的非负定性,但该方法只适用于随机风压场样本服从对数正态分布和韦布尔分布的情况。
上述已有方法虽然都能对非高斯时程进行模拟,但大多只能模拟单点非高斯时程,或是只能模拟满足特定条件的非高斯时程。本文作者对Huang等的单点非高斯风压模拟方法进行了改进,包括调整了原有谱修正方法中的相关参数,使算法能更快速收敛;另外利用苏宁等提出的四参数风压谱模型来构造大跨煤棚表面多点风压谱矩阵,提出了一种新的大跨煤棚网架非高斯风压场高效模拟方法。本文方法中只需要少数测点数据即可归纳得出煤棚表面风压经验谱,从而对整个大跨煤棚屋面非高斯风压场进行高效模拟,风压谱及非高斯特性的模拟精度均可以通过相关评价指标进行有效控制。以某大跨开敞式干煤棚网架风洞试验数据为基准,对多个代表性测点脉动风压的模拟结果进行了分析,验证了本文非高斯风压场模拟方法的精度和有效性。
1 非高斯风压场模拟理论
1.1 四参数风压谱模型
各测点风压系数按下式计算
(1)
式中:Cpi是测点i的净风压系数;Pi为测点i的风压值;P∞为参考点静压力值;V∞为参考点的风速。
风压时程的平均值和均方根分别按式(2)、式(3)计算
(2)
(3)
式中:Cpk为测点风压系数时程第k步的值,K为测点风压时程数据总数。
脉动风压系数自功率谱(PSD)采用四参数模型表示
(4)
(5)
式中:S为无量纲脉动风压系数自功率谱密度,f为频率(Hz),Scp(f)为脉动风压系数自功率谱密度,F为基于煤棚平均高度h以及该高度处来流平均风速Uh的折减频率,F′为无量纲频率,Sm、Fm、k1、k2为风压经验谱的四个参数,分别表示无量纲自功率谱的峰值、峰值频率、低频段上升斜率和高频段衰减斜率,四个参数的取值与屋盖形状、尺寸、测点位置和风向角有关,苏宁等认为一般情况下k1=1。α为待定参数,根据下式确定
(6)
式中:B(x,y)为Beta函数。
互功率谱(CPSD)表达式为
(7)
式中:SCpij为i,j两测点风压系数互功率谱,SCpi(f),SCpi(f)分别为i,j两测点风压系数的自功率谱密度函数,Δij为i,j两点间距,kc为衡量脉动风压场相干性的指数衰减系数,即相干系数。邵帅[18]根据多组风洞试验数据,建议开敞式大曲率拱形屋盖kc为3.5。
1.2 Hermite变换关系
基于Hermite矩的变换式是利用偏度和峰度来转换高斯过程与非高斯过程的关系式。其中Hermite矩正变换关系式如下
x=κ[u+h3(u2-1)+h4(u3-3u)];γ4>3
(8)
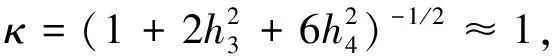
x为非高斯时程,u为高斯时程,γ3为偏度,γ4为峰度。
Hermite矩逆变换关系式如下
u=x-h3(x2-1)-h4(x3-3x);γ4<3
(9)
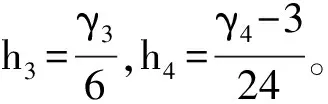
1.3 谐波叠加法
谐波叠加法是通过一组三角余弦函数的叠加来模拟稳态高斯过程的标准算法,具有完善的理论和较高的精度,合成公式如下
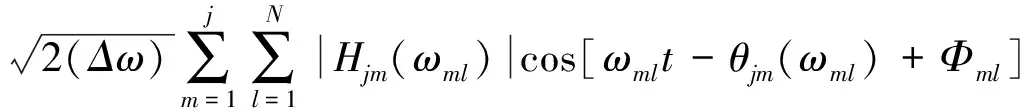
(10)
式中:fj(t)为t时刻j节点风压系数模拟值,Φml为均匀分布于[0,2π]上的独立随机相位角,ωu为截止圆频率,频率增量Δω=ωu/N,N为一个足够大的频率采样点个数。ωml的表达式如下
(11)
H(ω)为互功率谱矩阵S(ω)的Cholesky分解
S(ω)=H(ω)H*T(ω)
(12)
θjm(ω)为Hjm(ω)的幅角,即相位差。
2 非高斯风压场模拟算法
本文的非高斯风压场模拟算法流程图,如图1所示。详细步骤说明如下。
步骤1通过测压风洞试验,获取风压场数据试验样本
P(x,y,t)={p1(t),p2(t),…,pK(t)},减去各测点平均风压后得到目标脉动风压场数据样本
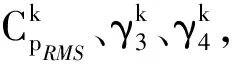
步骤3
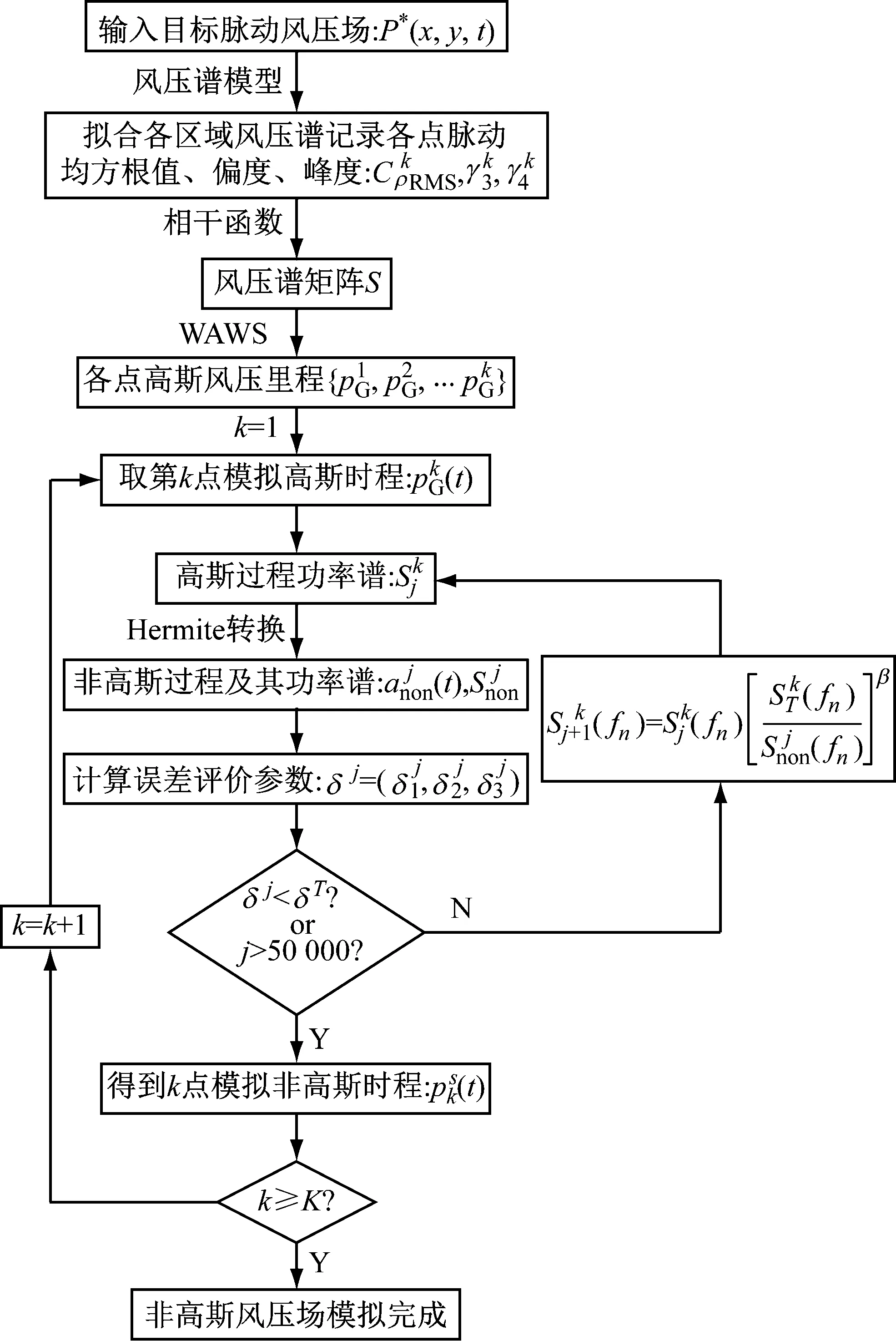
图1 非高斯风压场模拟算法流程图
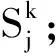
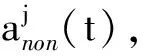

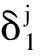
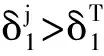
(13)
式中:β为修正常数,取值1.1,在保证精度的情况下使之快速收敛。利用修正功率谱模拟该点风压时程后返回至“(4)”,进行下一步迭代计算
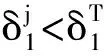
(7) 重复上述“(3)”~“(6)”,直至完成所有测点非高斯风压时程模拟。
3 某大跨开敞式干煤棚网架算例分析
3.1 风洞试验
某大跨开敞式干煤棚网架主体结构纵向长240 m,跨度120 m,总高度42.757 m。根据“建筑结构荷载规范:GB 50009—2012”,该煤棚处于A类地貌,地貌粗糙度指数α=0.12。百年一遇的基本风压为0.9 kPa,相当于离地面10 m高度处的设计风速U0=37.95 m/s。风洞试验在浙江大学ZD-1边界层风洞中进行,模型缩尺比为1∶150。模型表面布置了250对同步测量的内、外压测点,沿纵向分为25个测区,以编号A-Y(外表面)和AX-YX(内表面)表示。测压点布置图及风洞试验模型,如图2和图3所示。风洞试验中脉动风压测量采样频率为625 Hz,取30 s采样时长。对应原型的脉动风压时程数据时间步长为0.070 4 s,总时长为1 320 s。
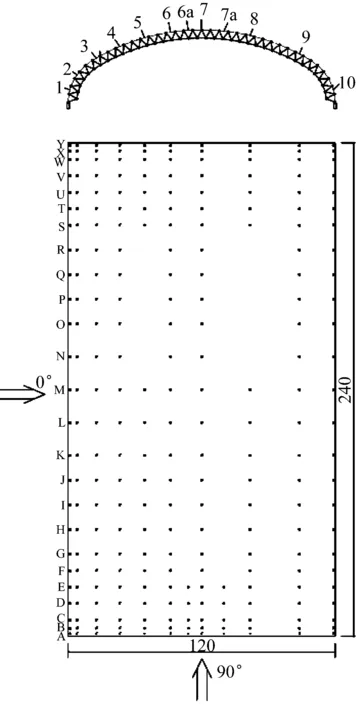
图2 测点布置图(m)

图3 风洞试验模型
图4为干煤棚表面平均风压系数及脉动风压系数均方根云图,从图4可知,两者有一定相似之处:在迎风侧,平均风压系数与脉动风压系数均方根值都比较大。在0°风向角下,煤棚顶部两者都比较小。但在背风侧的角点处,脉动风压系数均方根值有明显的增大。在90°风向角下,上游迎风侧煤棚两端脉动风压系数均方根值较大。

(a) 0°平均风压系数(b) 0°脉动风压系数

(c) 90°平均风压系数(d) 90°脉动风压系数
图4 平均风压与脉动风压均方根云图
Fig.4 Contour of mean and RMS values for fluctuating wind pressure
3.2 风压谱拟合
本文将0°风向角下煤棚表面分为三个区域,分区图如图5(a)所示,z为最小屋盖平面尺寸的10%和建筑高度的40%中的较小值。I区为迎风侧和顶部两端区域, II区为煤棚顶部中心区域, III区为背风侧。90°风向角下煤棚表面分为两个区域,分区图如图5(b)所示,绝大部分区域为迎风侧I区,靠近背风侧小块区域为III区。
由于屋盖表面的漩涡作用,各测点风压自功率谱与测点位置和风向角有关,图6给出了各测点无量纲风压功率谱的比较。0°风向角下,迎风侧测点受来流湍流影响较大,风压脉动能量集中在中低频处;在顶部的气流分离区,大尺度分离涡向小尺度涡转变,风荷载脉动频率较低,衰减较慢;而在背风侧尾部的再附区,风压受小尺度涡主导,峰值频率较高。90°风向角下,由于风洞试验工况为无煤堆工况,气流直接从内部穿过,风压脉动特性变化不大,大部分区域受来流湍流主导, 只有背风侧小部分区域,风压谱主导频率向高频移动。参考孙瑛所用分区,结合风洞试验所得干煤棚自身风压谱规律。

(a) 0°(b) 90°
图5 风压谱分区图
Fig.5 Zoning map for wind pressure spectra
对各区域所有测点无量纲风压谱进行拟合,为定量评价拟合结果,定义拟合误差ε为
(14)
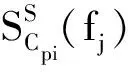
各区域拟合风压谱参数,见表1。从表1可知,0°风向角下,k1为前文所述取1,各区域无量纲风压谱的峰值Sm较为接近,但峰值频率Fm和衰减斜率k2有很大差别。II区Fm最小,即顶部风压能量集中在低频段,k2也最小;III区Fm最大,k2也最大;I区介于II区与III区之间,风压谱峰值不突出,能量分布较为均匀。90°风向角下,k1取大于1的值时拟合功率谱与实际谱较为接近;I区峰值Sm远大于III区峰值,与0°时各区峰值较为接近;对于峰值频率Fm,I区小于III区,与0°结果一致;衰减斜率k2则是I区大于III区。两个风向角下背风面风压谱离散性均较大,拟合精度略差于迎风面及顶部。
限于篇幅,本文仅对0°和90°两个代表性风向角进行分析和模拟。其他风向角也有类似规律,区别仅在于煤棚表面风压经验谱的分区及对应的四个谱参数不同,对不同风向角下煤棚表面进行重新分区和拟合后,可将本方法用于其他风向角。
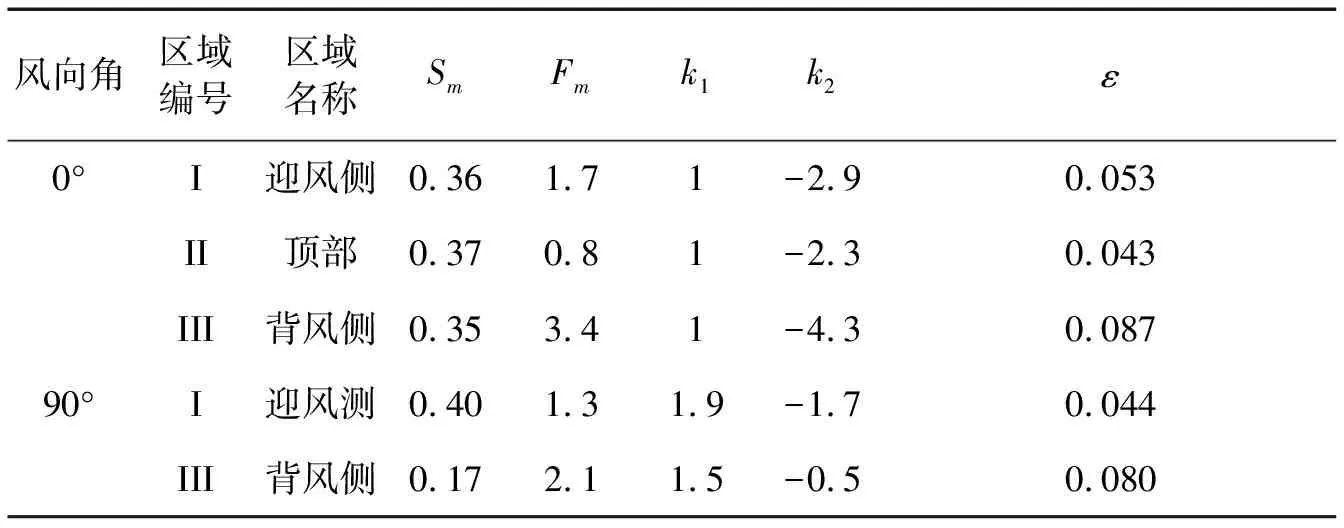
表1 煤棚表面各区域风压谱参数
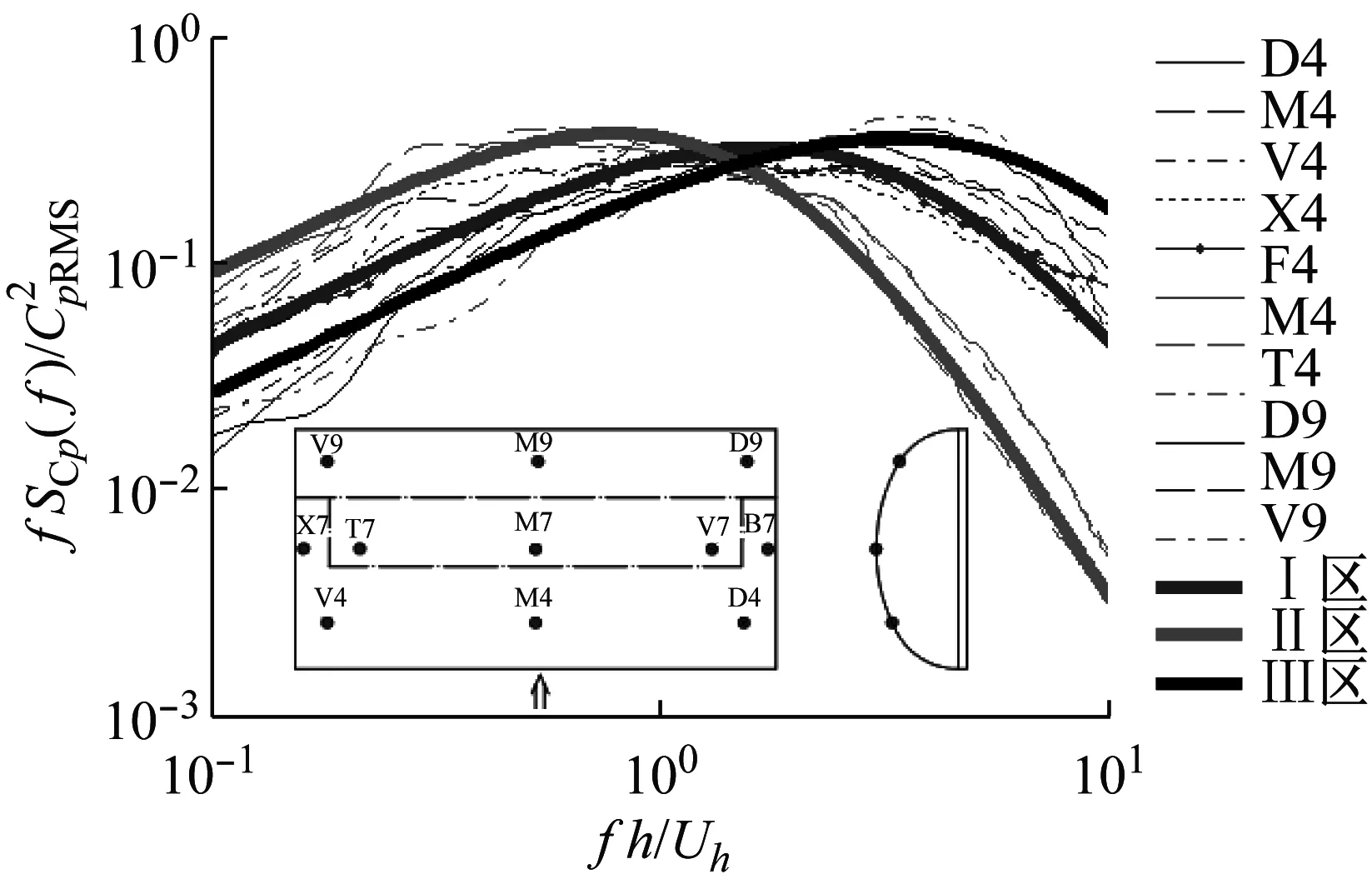
(a) 0°
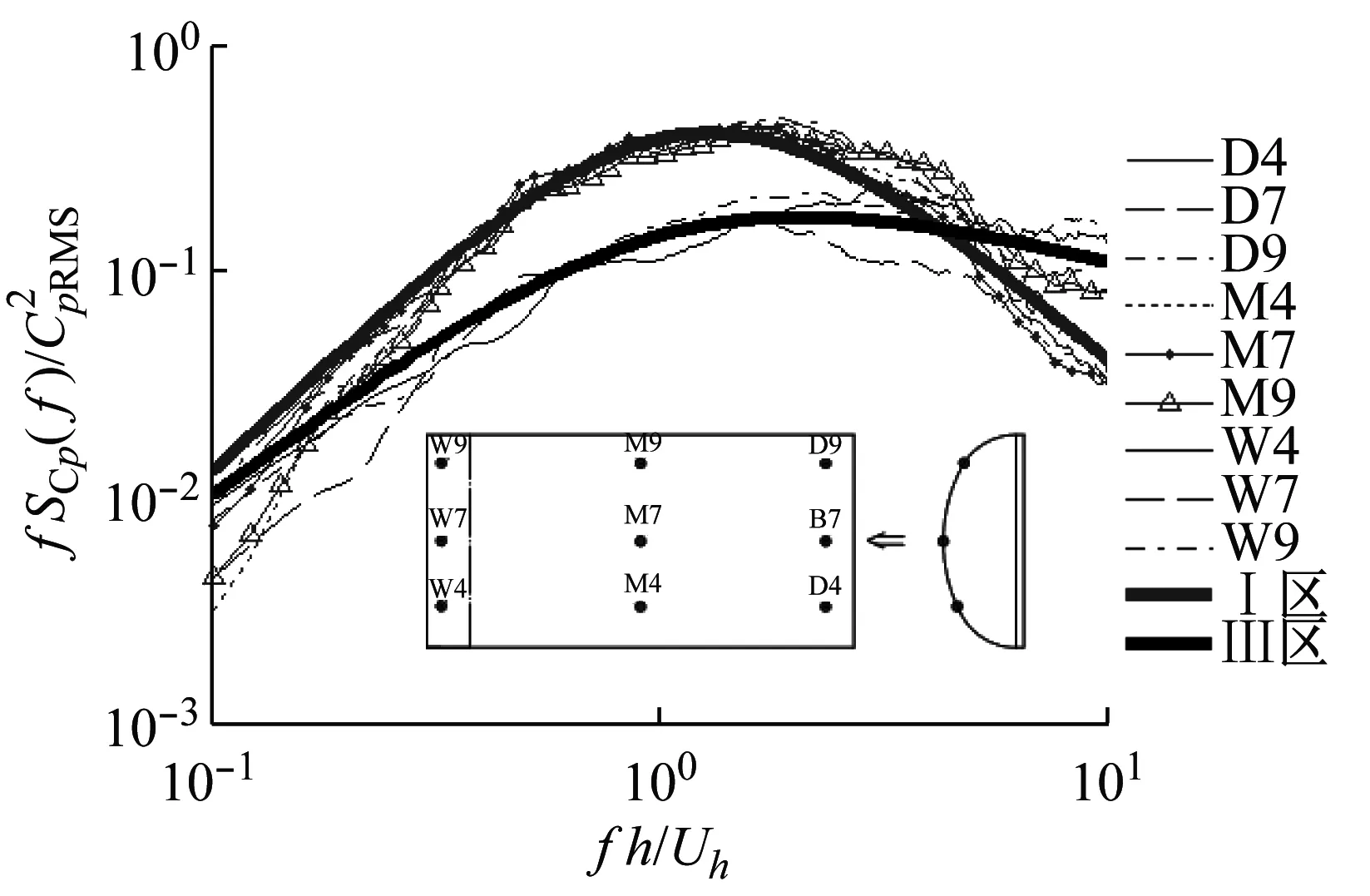
(b) 90°
3.3 模拟结果分析
3.3.1 测点脉动风压谱模拟结果分析
根据风洞试验结果,在各个区域选取脉动风压系数均方根值较大的代表性测点进行风压模拟和结果分析,0°风向角下选取L4、L8和L9,90°风向角下选取A7、S7和W7。图7给出了0°风向角下三个代表性测点模拟所得的脉动风压时程与风洞试验数据的比较。图8为各测点模拟所得脉动风压功率谱与风洞试验结果(目标谱)的比较。限于篇幅,时程比较只给出0°风向角下的结果。

(a) 测点L4
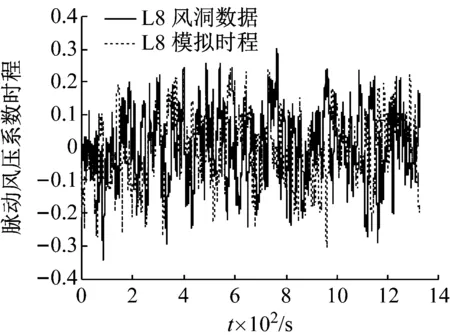
(b) 测点L8
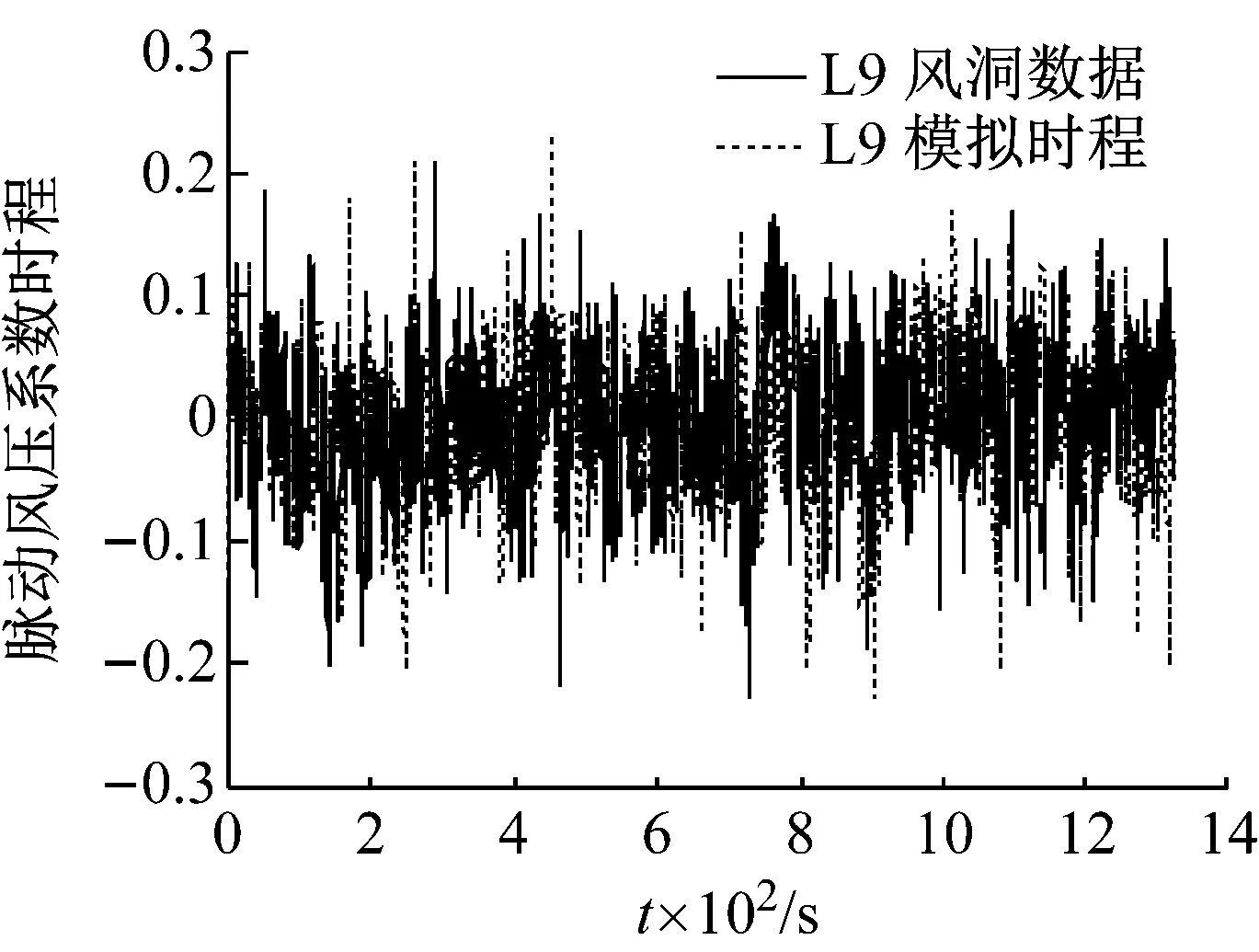
(c) 测点L9
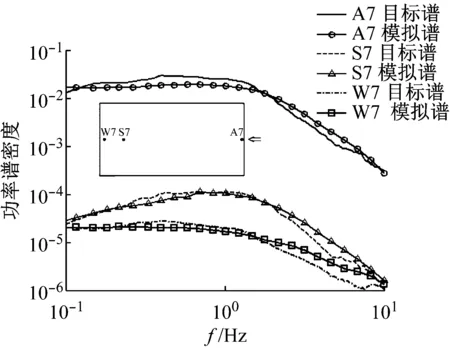
(b) 90°
从图7可知,各测点模拟所得的风压时程与风洞试验数据的波动形式较为一致。图8所示代表性测点模拟所得和风洞试验的风压谱也有较好的可比性。在0°风向角下,模拟所得脉动风压的功率谱在各个频段与风洞试验谱曲线均吻合较好,90°风向角下,模拟所得脉动风压的功率谱在高频段略大于风洞试验谱曲线,考虑到高频区域功率谱密度小能量低,模拟结果已较为理想。
为进一步评价脉动风压场的模拟结果,对不同测点之间的脉动风压相干性进行分析。0°风向角下选取代表性测点L8,90°风向角下选取代表性测点B7为考察对象,分别作出其与顺风向相邻测点与横风向相邻测点的互功率谱密度图,如图9和图10所示。从图中可以看出:0°风向角,沿着顺风向,模拟所得测点L8与L7脉动风压的互功率谱在低频区域略小于风洞试验谱曲线(目标谱)(见图9(a)),模拟所得测点L8与下游测点L9脉动风压的互功率谱与风洞试验谱曲线吻合程度较好(见图9(b));沿着横风向,模拟所得测点L8与K8、M8脉动风压的互功率谱在低频区域均略小于风洞试验谱曲线(见图10(a)、图10(b)),在高频区域则吻合较好。90°风向角下,模拟所得测点B7与顺风向测点A7、C7脉动风压的互功率谱与风洞试验谱曲线吻合程度较好(见图9(c)、图9(d));沿着横风向,所考察测点B7与横风向测点B6和B8的模拟所得脉动风压的互功率谱在各个频段均略小于目标风洞试验谱曲线(见图10(c)、图10(d))。由于本文模拟方法中风压互功率谱其相干系数取值均为3.5,不能区分不同风向角下沿着不同方向上风压相干性的差异。这样导致模拟所得各测点脉动风压之间的互功率谱与实际风洞试验的谱曲线有一定差距,值得在将来的工作中研究改进。
3.3.2 测点脉动风压非高斯特性分析
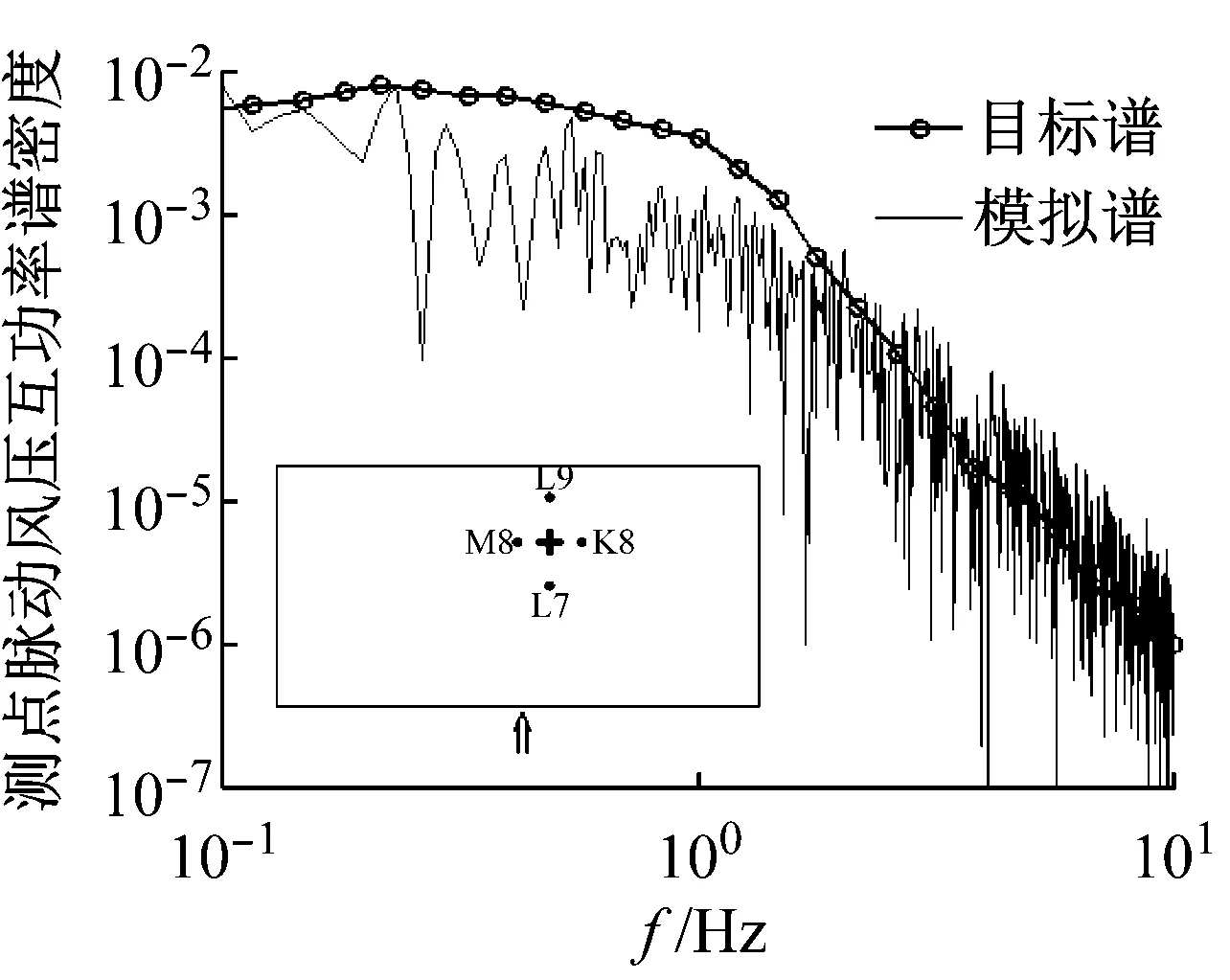
(a) 测点L8和L7(0°风向角)
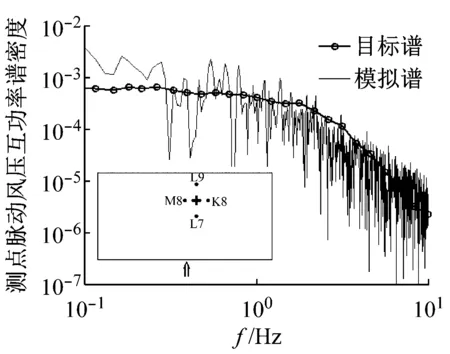
(b) 测点L8和L9(0°风向角)
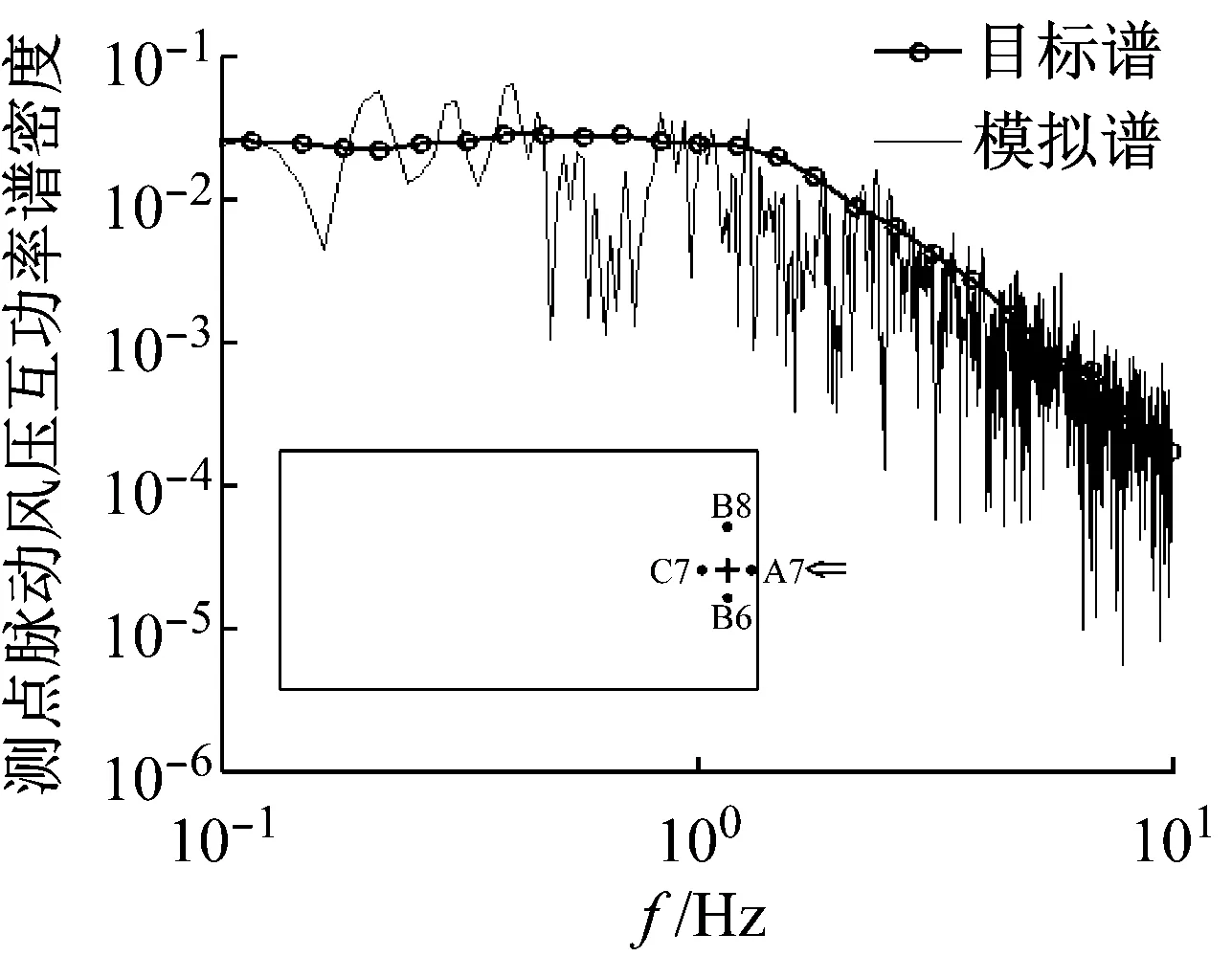
(c) 测点B7和A7(90°风向角)

(d) 测点B7和C7(90°风向角)
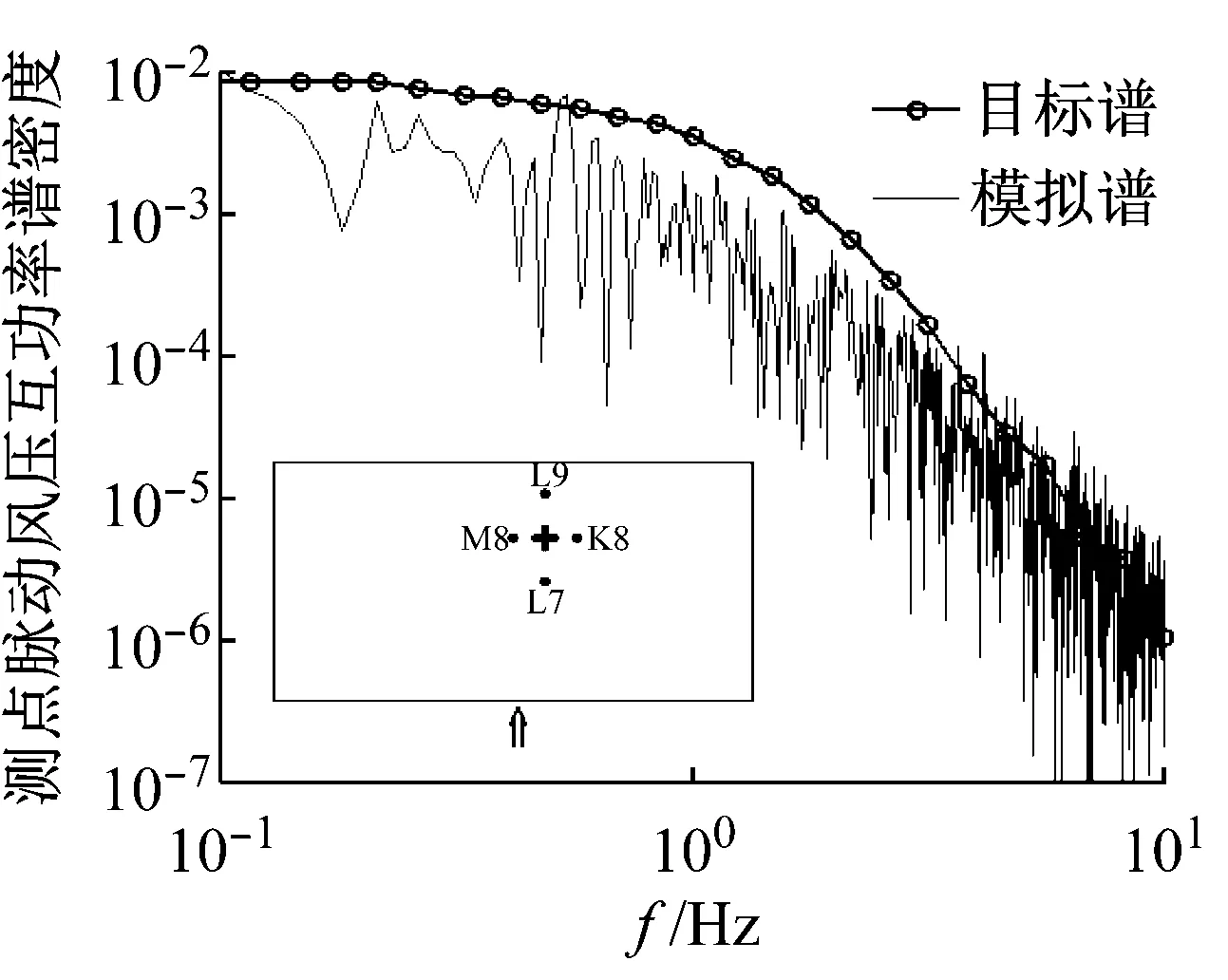
(a) 测点L8和K8(0°风向角)
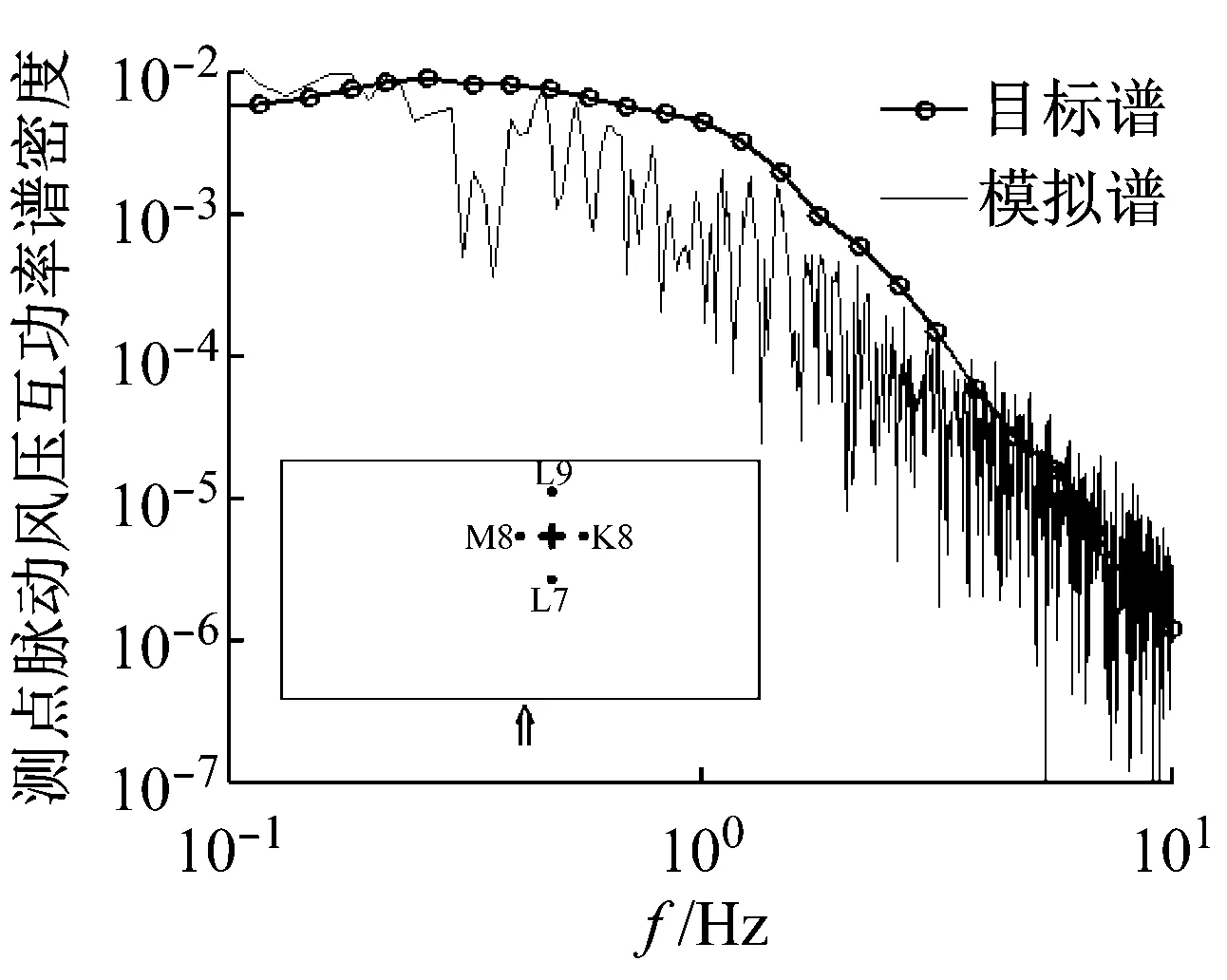
(b) 测点L8和M8(0°风向角)
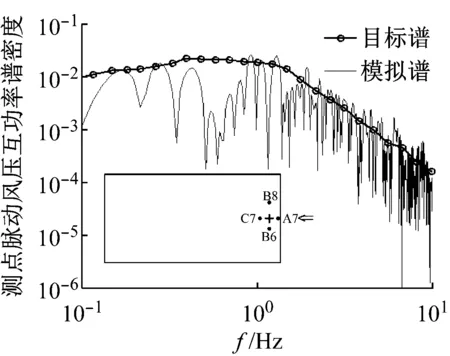
(c) 测点B7和B6(90°风向角)
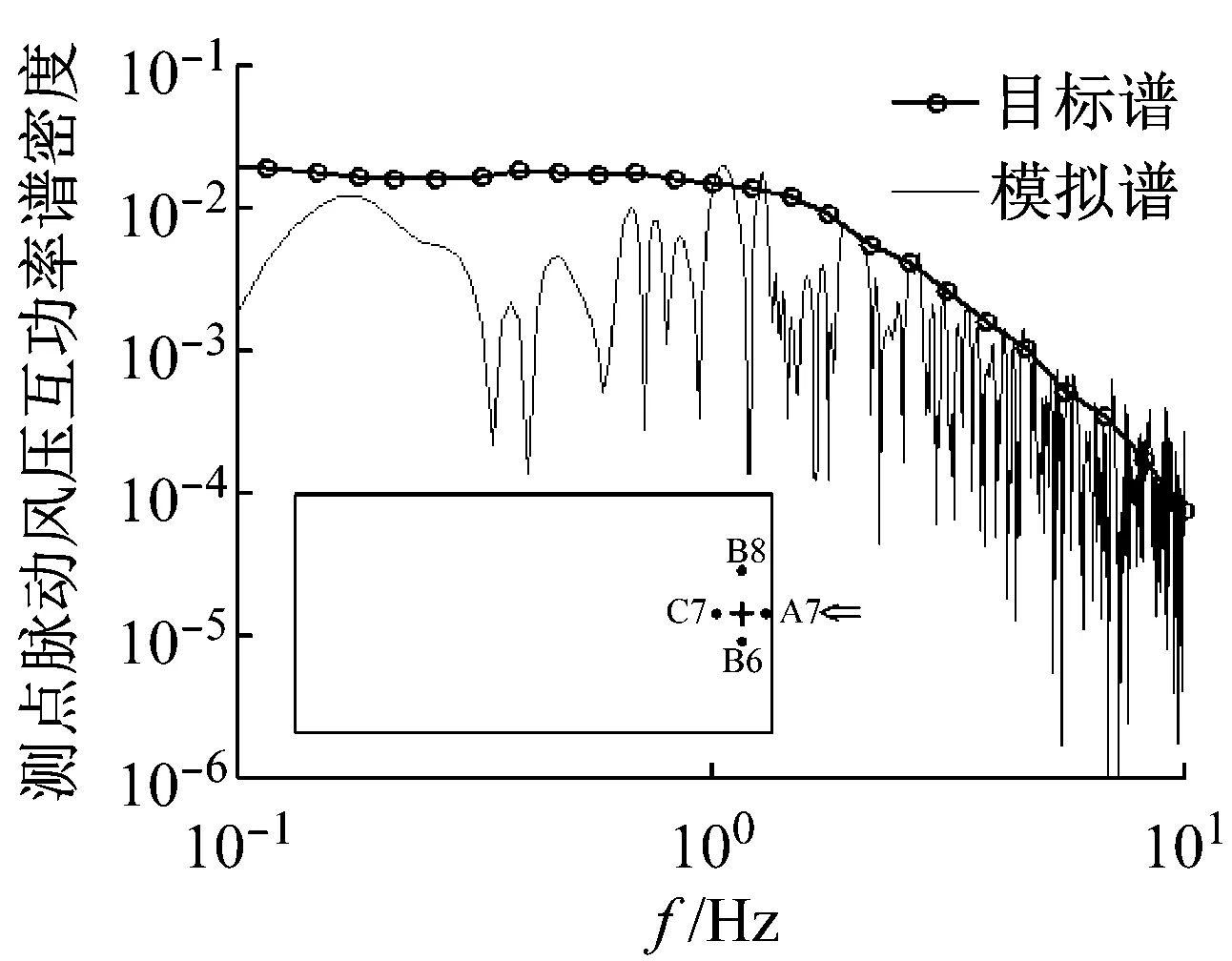
(d) 测点B7和B8(90°风向角)
为评价脉动风压场的非高斯特性,对测点脉动风压的高阶统计量进行了分析。图11为0°风向角下脉动风压场的偏度及峰度等值线云图,其中图11(a)和图11(c)为根据风洞试验测压数据获得的偏度和峰度分布图,图11(b)和图11(d)为基于模拟所得风压场数据得出的偏度和峰度分布。从图11可知,模拟所得高阶统计量分布云图与试验结果较为吻合。根据试验所得各测点脉动风压高阶统计量,在0°和90°风向角下各选取4个具有较强非高斯性的测点(即,绝对偏度>0.5,峰度>4)。表2为选取测点的偏度和峰度模拟值和风洞试验数据比较。表2的结果说明各代表性测点高阶统计量的模拟值与试验值比较吻合。因为在本文方法中采用具有解析模式的Hermite变换关系,即式(8),得到相应的非高斯时程数据,通过反复的迭代修正,其高阶统计量可与风洞试验目标值非常接近,满足给定的误差要求。

(a) 试验所得偏度分布(b) 模拟所得偏度分布
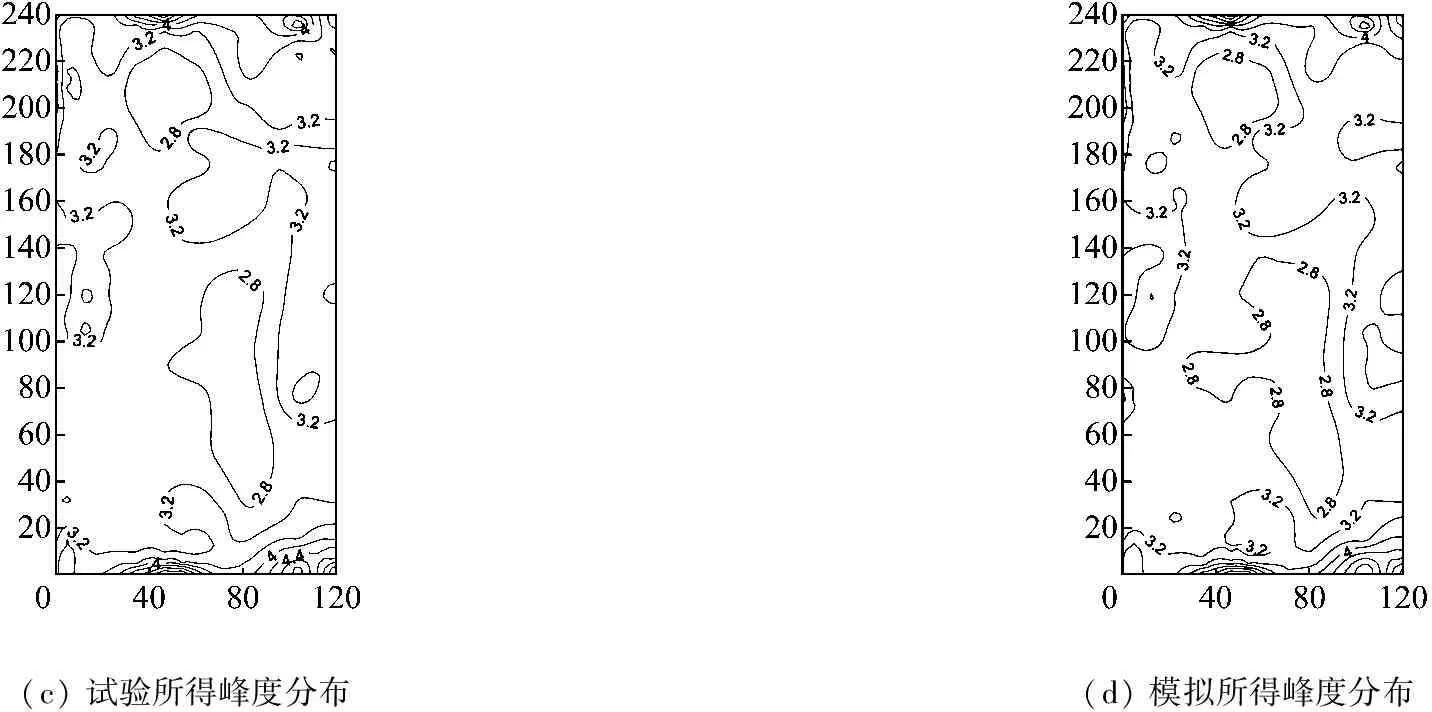
(c) 试验所得峰度分布(d) 模拟所得峰度分布
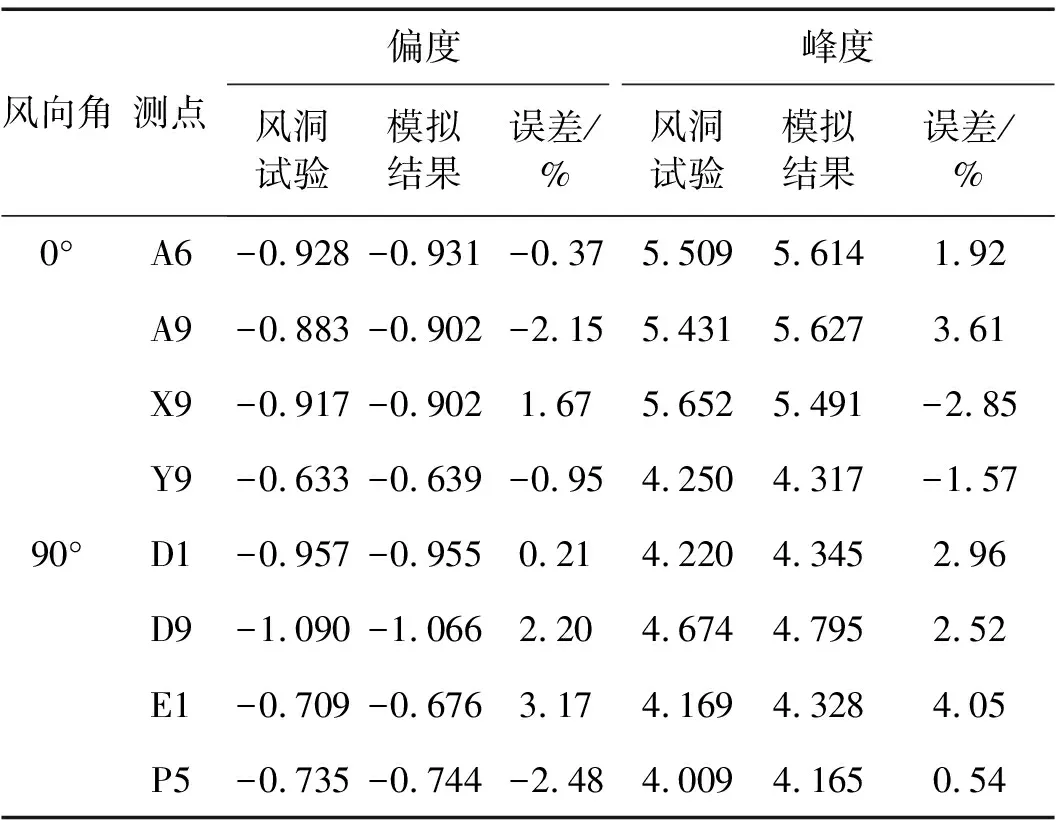
图11 0°风向角下脉动风压场偏度与峰度的分布云图比较
为比较本文方法与已有相关算法的优缺点,利用李璟等的三次多项式转换法对90°风向角下干煤棚4个代表性测点的非高斯脉动风压进行模拟结果,如表3所示。对比表2结果可知,本文方法模拟所得非高斯风压场在偏度和峰度指标上的精度均明显高于三次多项式转换法。
表3李璟方法代表性测点脉动风压高阶统计量比较
Tab.3ComparisonofthesimulatedandmeasuredhigherorderstatisticsforrepresentativemeasurementtapsbyLiJ’smethod
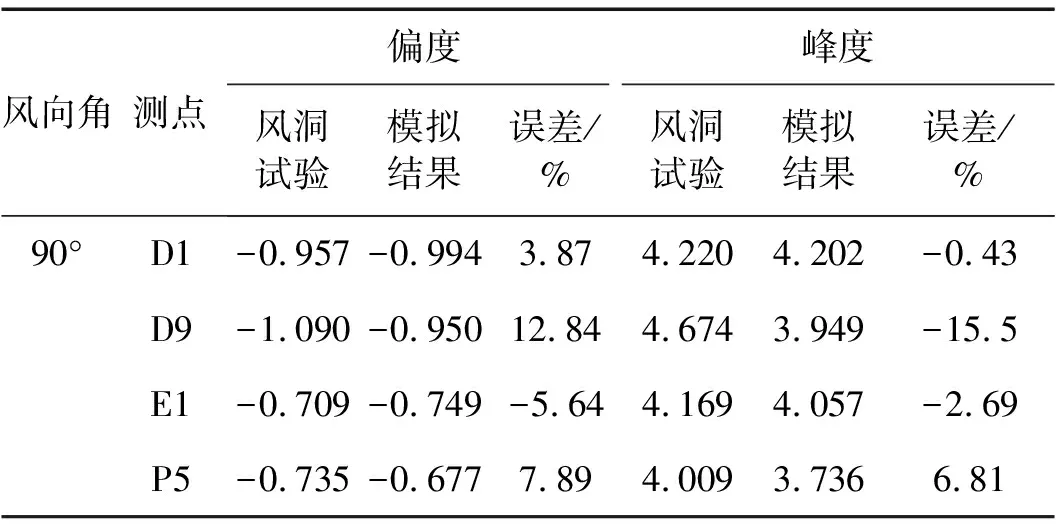
风向角测点偏度峰度风洞试验模拟结果误差/%风洞试验模拟结果误差/%90°D1-0.957-0.9943.874.2204.202-0.43D9-1.090-0.95012.844.6743.949-15.5E1-0.709-0.749-5.644.1694.057-2.69P5-0.735-0.6777.894.0093.7366.81
4 结 论
本文提出了一种基于经验风压谱和Hermite模型的大跨干煤棚非高斯风压场模拟算法,并以某干煤棚网架结构风洞试验为工程实例,对非高斯风压场模拟结果进行了分析和验证。主要结论如下:
(1) 大跨干煤棚屋面经验风压谱可根据所处位置分成若干个区域,各区域的无量纲风压谱峰值频率和形状有较大不同。本文给出了不同风向角下干煤棚屋面各区域的划分方法和确定每个区域经验风压谱的四个参数。因此,仅需要个别点位的风压风洞试验数据就可以归纳得出基本覆盖整个干煤棚屋面的经验风压谱,并可以根据相应的经验风压谱开展大跨干煤棚非高斯风压场模拟,获得任意位置的风压时程数据样本。
(2) 数值模拟计算得到的测点脉动风压时程在自功率谱密度上与风洞试验谱差别不大,但相邻风压测点之间的互功率谱密度与风洞试验谱曲线还存在一定差距。而且不同风向角下的模拟结果精度也有所不同,这个主要是由于不同风向角下沿着不同方向上屋面风压场相干性的不同而造成的。本文采用的风压互功率谱其相干系数取值均为3.5,可以在后续工作中考虑取不同的相关系数来反映不同风向角下风压场相干性的差别。
(3) 在衡量脉动风压场非高斯特性的高阶统计量上,无论是偏度还是峰度指标,对比已有方法,本文方法模拟所得的多点风压时程数据结果与风洞试验目标值吻合程度都较好,说明本文方法在非高斯风压场模拟方面具有较高的精度。
(4) 本文算例利用某大跨干煤棚风洞试验数据归纳得到了干煤棚表面的风压谱分区和参数取值,完成了大跨干煤棚非高斯风压场的数值模拟。但本文方法并不仅仅适用于大跨干煤棚。利用其他大跨建筑的风洞试验数据或相关资料可以对本文采用的干煤棚表面风压经验谱分区和各区域风压谱参数进行修改,这样该方法即可推广应用至其他大跨屋盖建筑非高斯风压场的模拟。
