基于集成阶频谱相关的滚动轴承故障特征提取
2018-12-21夏均忠汪治安陈成法吕麒鹏刘鲲鹏
夏均忠, 汪治安, 陈成法, 吕麒鹏, 刘鲲鹏
(军事交通学院 军用车辆工程技术研究中心,天津 300161)
滚动轴承是大部分旋转机械的重要零部件,其出现故障的概率较高[1],带来的后果严重,因而对滚动轴承的故障诊断一直是研究的热点问题,振动分析方法是滚动轴承故障诊断的主要方式[2]。
近年来,循环平稳理论在滚动轴承和齿轮箱的故障诊断中扮演着十分重要的角色[3-5]。在循环平稳统计量中,谱相关密度函数(以下简称谱相关)是提取滚动轴承故障特征的主要统计量[6]。Borghesani[7]提出了基于循环调制谱的谱相关估计方法,并对其估计质量作了详细的分析,相比于传统的谱相关估计方法,该方法在一定程度上提高了估计效率。Urbanek等[8]通过对调制密度分布的谱频率轴积分得到集成调制密度分布(Integrated Modulation Intensity Distribution, IMID),降低了故障特征的维数,简化了故障特征的表达。在工业实际应用中,由于载荷波动和工况变化,轴承的运行转速难以保持恒定,轴承的故障特征频率随时间而变化,传统的循环谱相关分析方法主要建立在定转速或者小转速波动的假设基础上,难以应用于变转速工况下滚动轴承故障特征[9]。
Abboud等[10-14]在循环平稳的基础上,提出了角度/时间循环平稳(Angle/Time Cyclostationary, ATCS),利用阶频谱相关(Order-frequency Spectral Correlation, OFSC)表征变转速下滚动轴承故障特征,为循环平稳在变转速工况下的滚动轴承故障诊断奠定了基础。
针对变转速工况下的滚动轴承故障特征提取,论文在研究AT-CS的基础上,将循环调制谱(Cyclic Modulation Spectrum, CMS)应用到阶频谱相关的估计中,得到基于循环调制谱的阶频谱相关,在此基础上,将阶频谱相关加以改进,提出基于集成阶频谱相关(Integrated Order-frequency Spectral Correlation, IOFSC)的滚动轴承故障特征提取方法。改进后的方法只提取故障特征阶次,使阶频谱相关对故障特征的表达由三维变为二维。
1 角度/时间循环平稳理论
1.1 AT-CS信号
对于非平稳信号随机过程x(t),将时变自相关函数中的时间变量用角位移变量代替,可以得到角度/时间自相关函数(Angle/Time Correlation Function,ATCF)
R2x(τ,θ)=Ε{x(t(θ))x(t(θ)-τ)*}=
R2x(τ,t(θ))
(1)
式中:τ表示时间延迟;Ε表示集总平均运算。时间t和角位移θ存在下列关系
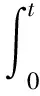
(2)
式中:ω(t)为瞬时角速度。
如果信号的ATCF具有周期性,并且在循环阶β处存在非零傅里叶系数,那么这个信号是角度/时间循环平稳(AT-CS)信号
(3)

此时AT-CS信号可以用下式来表示
(4)

在变转速条件下,故障冲击的时域周期性消失,角域的周期性却不受转速的影响,但是冲击响应依然只取决于时间变量,因此,变转速下滚动轴承的故障信号具有角度/时间循环平稳特性,是一种AT-CS信号。
1.2 阶频谱相关
阶频谱相关(OFSC)定义为ATCF的二次傅里叶变换,第一次傅里叶变换将信号从时域映射到频域,第二次傅里叶变换将信号从角域映射到阶域
(5)
式中:α为循环阶,它是一个没有单位的量,表示轴每旋转一周某事件发生的次数。对于滚动轴承的故障诊断,可以理解为轴每旋转一周故障冲击产生的次数。
由于t和θ存在式(2)的关系,因此,OFSC可表示为
(6)

对于AT-CS信号,其阶频谱相关具有如下性质
(7)
由式(7)可知,OFSC是关于α和f三维map图,其中循环阶α显示了信号中的角域循环调制成分,表示故障信息,谱频率f则表示信号的载波成分。将α与计算的理论故障阶次进行对比,即可判断出滚动轴承的故障类型,实现变转速工况下的故障特征提取。
1.3 基于循环调制谱的阶频谱相关
为了提高阶频谱相关的估计效率,将循环调制谱估计方法应用到角度/时间循环平稳信号中,实现基于循环调制谱的阶频谱相关估计。
首先,通过短时傅里叶变换得到信号的时频瞬时功率谱(Time-Frequency Instaneous Power Spectrum,TF-IPS),并进行归一化处理,完成第一次傅里叶变换
(8)

其次,通过对时频瞬时功率谱中的时间变量进行阶比跟踪得到角频瞬时功率谱(Angle-Frequency Instaneous Power Spectrum,AF-IPS)
(9)
式中:θm=mΔθ;COTΔt→Δθ{·}为等角度重采样。为了避免混叠现象的产生,等角度采样的分辨率Δθ需满足
Δθ≤ωminΔt
(10)
式中:ωmin为信号采集过程中的最小角速度;Δθ必须小于原采样中的最小角度增量。利用采集的角位移信号Ω(t),通过插值运算实现重采样过程。
最后,对角频瞬时功率谱进行离散傅里叶变换得到基于循环调制谱估计的阶频谱相关
(11)

2 集成阶频谱相关
阶频谱相关是关于载频f和阶次α的函数,通过三维图的方式表达故障特征。在滚动轴承的故障诊断中,关注的是能够反映调制(故障)特征的阶次信息,而常常忽略载频信息。对阶频谱相关的响应频带进行积分以获得集成阶频谱相关(IOFSC),其表达式为
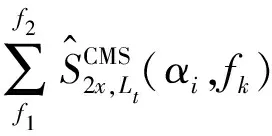
(12)
由阶频谱相关得到故障响应的频率区间[f1,f2],以此作为积分区间,得到集成阶频谱相关,不仅降低了特征表达的维度,而且通过选择合适的积分频带,排除了多余成分的干扰,使得故障特征更加突出。其过程示意图,如图1所示。

图1 集成阶频谱相关示意图
基于集成阶频谱相关的滚动轴承故障特征提取流程,如图2所示。其主要步骤包括:
(1) 通过循环调制谱计算信号的阶频谱相关(OFSC)。
(2) 观察分析阶频谱相关,得出响应频率区间[f1,f2],并以此为积分频带计算信号的集成阶频谱相关(IOFSC)。
(3) 通过对集成阶频谱相关中的阶次分布与理论故障特征阶次对比,判断故障类型。
集成阶频谱相关的算法计算包括短时傅里叶变换、阶比跟踪和积分运算。其中短时傅里叶变换主要包含S次点数为Nh的离散傅里叶变换;略去插值过程,第二次傅里叶变换主要包括Nh次点数为Sθ离散傅里叶变换;积分运算主要是加法运算,其计算量也可以略去,因此整个算法的计算复杂度约为
OCMS≈SNhlog2Nh+NhSθlog2Sθ
(13)
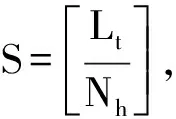

图2 基于IOFSC的滚动轴承故障特征提取流程
3 仿真分析
变转速条件下的滚动轴承故障信号仿真模型为
x(t)=x1(t)+x2(t)+n(t)=
(14)
滚动轴承的振动信号x(t)由变转速下的故障冲击信号x1(t)、转频及其谐波信号x2(t)和高斯白噪声n(t)组成[15]。Ai表示第i次冲击对应的幅值,幅值受到转频的调制,其与转频满足线性关系:Ai=a·vi+b;s(t)=e-βtcos(2πfnt)为故障的冲击响应;Ti为第i次冲击发生的时刻;τi表示相邻冲击之间相对的滑移;Bm和φm分别表示m次谐波的幅值和初始相位。
设模拟的轴承外圈故障特征阶次为F0=3.5,轴承的转频方程为f(t)=9t+45。在振动信号中加入3个谐波分量,其幅值和相位分别为:B1=0.4,φ1=π/4;B2=0.6,φ2=-π/2;B3=0.8,φ3=π/3。仿真模型参数设置见表1。

表1 仿真模型参数设置
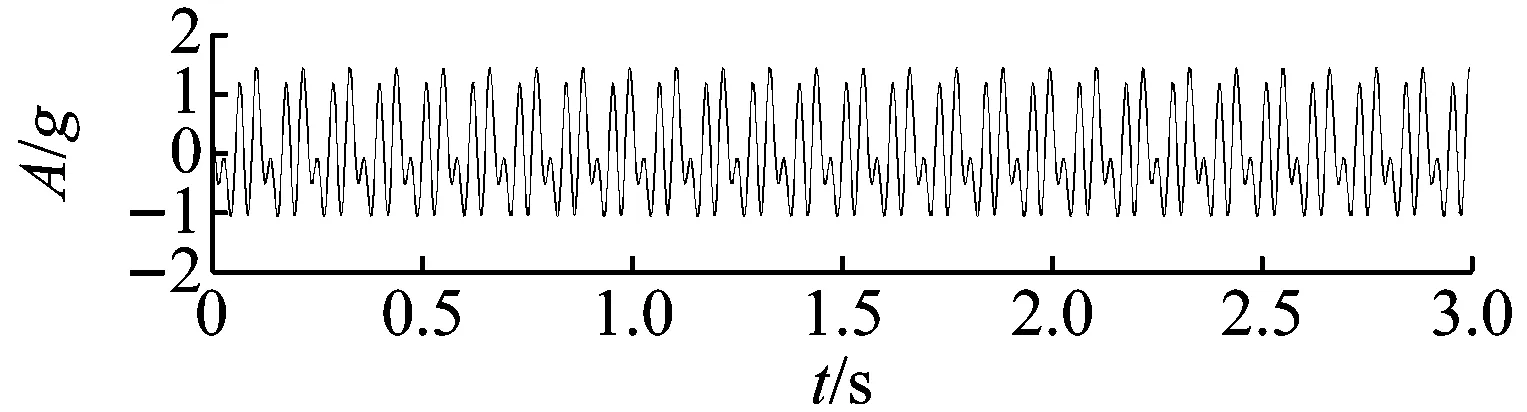
由上述仿真模型及参数得到的轴承故障仿真信号,如图3所示。从图3(a)可知,随着转速的提升,振动信号的幅值逐渐增大,故障冲击不再满足等时间间隔,这样的冲击序列具有角度/时间循环平稳的特征,是AT-CS信号。在转频及其谐波成分(见图3(b))以及强噪声(见图3(c))的干扰下,难以从时域波形中(见图3(d))分辨出转速的调制现象与故障冲击特征。

(a) 冲击序列
(b) 转频谐波

(c) 高斯噪声

(d) 合成信号
由于轴承转速波动较大,传统的循环平稳方法难以从中提取故障特征。图4为仿真信号的循环谱相关计算结果。经观察发现,在f轴上循环谱相关能量主要分布在共振频率fn(2 000 Hz)附近,但是从α(此时单位为Hz)轴上却没有发现与故障特征频率对应的谱线。说明在变转速工况下,受到转速变化的影响,循环谱相关无法提取二阶循环平稳成分,难以提取滚动轴承故障特征。

图4 仿真信号的循环谱相关
利用循环谱估计方法计算仿真信号的阶频谱相关,得到变转速下滚动轴承故障仿真信号的阶频谱相关map图,如图5所示。从图5中的α(此时单位为order)轴上可以清晰地分辨出预设的故障阶次F0及其谐波对应的谱线,并且谱线的能量主要分布在预设的系统共振频率fn附近(1 500~2 500 Hz),说明该方法能有效提取变转速下滚动轴承故障特征,但是该故障特征同时包含了载频信息f和特征阶次信息α,在表达上不够简洁直观。

图5 仿真信号的阶频谱相关
在阶频谱相关的基础上计算信号的集成阶频谱相关,取积分频带为[1 500,2 500]Hz,结果如图6所示。集成阶频谱相关将阶频谱相关包含的特征信息由三维降低到二维,具有更清晰直观的表达效果。通过选择合适的积分频段,可以进一步降低噪声成分的干扰,具有更强的抗噪能力。

图6 仿真信号的集成阶频谱相关
4 实验验证
实验装置主要由三相驱动电机、变频控制器、驱动轴、从动轴等组成[16]。通过变频器控制电机转频在10~20 Hz。实验采用NI公司的NI-USB-6211 16位的A/D数据采集卡。采样频率为50 kHz,采样时间为21 s。
试验轴承安装在从动轴上,其主要技术参数见表2。分别在3个轴承上加工了外圈、内圈、滚动体故障,故障深度为1 mm,边长为3 mm,截面形状为正方形。通过计算可以得到滚动轴承的故障特征阶次,见表3。

表2 试验轴承技术参数

表3 轴承故障特征阶次
不同故障轴承实验的转速曲线和振动信号时域波形,分别如图7、图8所示。滚动轴承的振动信号受到转频的调制,相比于稳速条件下的振动信号表现出更加复杂的调制现象。
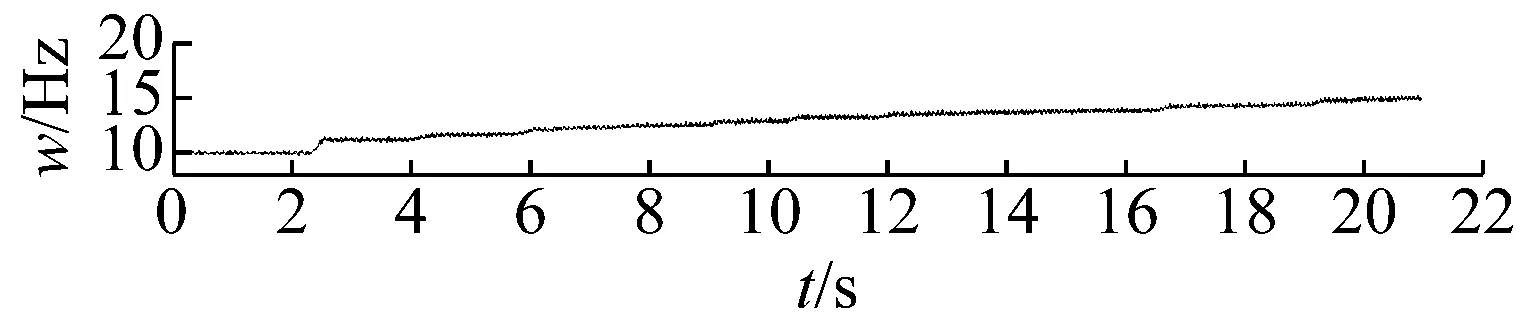
(a) 外圈故障

(b) 内圈故障

(c) 滚动体故障

(a) 外圈故障

(b) 内圈故障

(c) 滚动体故障
对三种技术状态的轴承进行循环谱相关分析,相应的循环谱相关,如图9所示。从f轴上可以发现系统的响应在100~400 Hz之间,但是能量并不集中;在α轴上没有出现平行的谱线,也没有与故障特征频率相关的谱线。这说明循环谱相关无法应用于变转速工况下的滚动轴承故障特征提取。

图9 故障轴承振动信号的循环谱相关
用基于循环调制谱的阶频谱相关分析三种技术状态轴承振动信号,得到的结果,如图10所示。在理论故障特征阶次、转频及其谐波对应的循环阶处,存在幅值明显的谱线,而在其他循环阶处几乎不存在谱线。阶频谱相关可以有效提取AT-CS信号的角域周期性,实现变转速工况下滚动轴承故障特征。

(a) 外圈故障

(b) 内圈故障

(c) 滚动体故障

(a) 外圈故障

(b) 内圈故障

(c) 滚动体故障
选取积分频带为[100,400]Hz,计算三种技术状态轴承振动信号的集成阶频谱相关,如图11所示。从图中可以分辨出不同故障所对应的理论故障特征阶次及其谐波,转频及其谐波。相比于阶频谱相关,集成阶频谱相关的维数更低,且具有更清晰直观的表达效果。
5 结 论
(1) 变转速工况下,故障轴承的振动信号具有角度/时间循环平稳特性,循环谱相关不能有效提取振动信号中的二阶循环平稳成分。
(2) 循环调制谱可以实现变转速下振动信号的阶频谱相关估计,并且具有计算效率高,应用简单的特点。
(3) 基于AT-CS的阶频谱相关可以有效提取变转速下滚动轴承故障特征,集成阶频谱相关是对阶频谱相关进一步改进,降低了特征数据的维数,能够更清晰直观的表达故障特征。
