迭代广义解调齿轮信号分离的变转速滚动轴承故障诊断

2018-12-21李红贤汤宝平

振动与冲击 2018年23期

李红贤，汤宝平，韩延，邓蕾

(重庆大学机械传动国家重点实验室，重庆 400030)

滚动轴承作为旋转机械的关键零部件，其安全平稳的运行会影响机器的整体性能，因此，对滚动轴承进行状态监测和故障诊断具有极其重要的意义[1-2]。齿轮啮合干扰和变转速工作模式是影响滚动轴承故障诊断较为常见的两大因素，齿轮啮合会对轴承故障冲击产生掩盖，降低了轴故障轴承冲击特征，变转速使得故障轴承不再以等间隔产生冲击，传统的频谱分析方法将不再适用[3-4]。

为了解决变转速工作模式下齿轮啮合对轴承造成的干扰，一些学者进行了探索。文献[5]采用齿轮角域重采样-齿轮带通滤波消噪-时域逆采样的方式去除齿轮信号干扰，再对剩余信号进行阶次谱故障判别，但该方法计算过程较为繁琐，对重采样到角域的信号进行带通滤波会削弱轴承故障冲击特征，且该方法受转速计的限制。文献[6]提出了改进的自适应消噪算法消除齿轮信号对轴承共振带影响，以提取的瞬时故障特征频率曲线等效为轴承转频做角域重采样，摆脱了对转速计的依赖，但该算法只以幅值最大的齿轮啮合倍频信号作为参考信号予以消除，无法消除其它齿轮啮合频率信号，且齿轮信号消除不干净会直接干扰瞬时故障特征频率曲线的提取，对滚动轴承的故障诊断产生影响。文献[7]提出以IDMM(Instantaneous Dominant Mesthing Multiply)趋势线作为轴承转频做重采样，再通过EMD分解分离出齿轮干扰信号，以IDMM趋势做重采样摆脱了受转速计的限制且避免了因齿轮去除不干净而造成的影响，但EMD存在模态混叠、端点效应等缺陷，所选层数并不能完全去除齿轮信号干扰且会丢失部分轴承故障信息。旋转机械通常存在多对齿轮，且齿轮相互啮合会产生多个啮合频率及倍频信号，只是对某些瞬时啮合频率信号进行分离，并不能完全消除齿轮对轴承的干扰。

广义解调算法可以将频率变化的时变信号解调为频率恒定的平稳信号，通过窄带滤波可有效地提取变频信号。文献[8]通过迭代广义解调提取出变转速下行星齿轮各阶啮合频率信号，采用同步压缩时频分析方法进行故障诊断。文献[9]通过迭代广义解调和能量分离算法精确的获取了信号的瞬时频率。迭代广义解调可以分离出齿轮的啮合频率及其倍频信号，但广义解调相位函数的获取依赖于转速计辅助，在实际应用中受安装空间和安装成本的制约。利用IDMM趋势线可以有效地摆脱广义解调算法对转速计的依赖，通过该趋势线构造各广义解调函数的相位函数，并将趋势线等效为轴承转频进行角域重采样，实现了无转速计下变转速滚动轴承故障诊断。

1 迭代广义解调齿轮信号分离

1.1 广义解调算法原理

广义解调算法是一种新的处理时变信号的方法，根据单一信号的瞬时相位构造解调函数，将非周期的时变信号转化为频率恒定的周期信号[10]。广义解调算法的本质为广义傅里叶变换，对于信号x(t)，其广义傅里叶变换的定义为

(1)

式中：s0(t)为与时间t相关的实值函数，这实际是根据信号的瞬时相位，构造一个解调函数与信号相乘，也就是对x(t)e-2πjs0(t)做标准的傅里叶变换。分析信号为x(t)=e-2πj(f0+s0(t))。因此，将变频信号转化为频率恒定的平稳信号，时变的相位函数需要满足式(2)的关系

(2)

1.2 迭代广义解调齿轮信号分离

实测信号往往由多个瞬时频率变化不一的多分量信号构成，仅仅依靠一次广义解调无法将多分量信号解调为频率恒定的平稳信号，通过迭代的方法，就可以依次分离出各分量信号。齿轮啮合时会产生啮合频率及倍频信号，通过迭代广义解调算法可以提取齿轮啮合频率及倍频信号分量，有效地削弱齿轮对轴承产生的干扰，而传统广义解调算法的相位函数需要通过转速计进行获取，为了摆脱对转速计的依赖，在对齿轮信号分离时，根据齿轮瞬时啮合频率(Instantaneous Meshing Frequency, IMF)及其倍频信号在包络时频谱(Envelope time frequency representation, ETFR)中具有突出峰值特点，采用峰值搜索算法提取幅值最大的齿轮啮合频率曲线，在不使用转速计等辅助设备的情况下，完成对解调信号瞬时相位的间接获取。

首先，对混合信号义进行Hilbert变换获取包络信号，利用短时傅里叶变换得到ETFR结果，公式如下

(3)

式中：x(τ)表示故障轴承的振动信号；g(τ)为高斯窗函数。

其次，通过峰值搜索算法从ETFR中寻找幅值最大所对应的频率值和时刻点，在信号时间范围内获得各ti时刻瞬时频率值IFSi，再将各时刻点的IFSi按照时间顺序相连接便得到IDMM趋势线

IFCFi=argmax{IFSi}(i=1,2,…,n)

(4)

式中：IFS(Instantaneous Frequency Spectrum)为瞬时频谱；i为IFS对应的序号,取值是1～n；argmax函数表示IFSi取得最大值时对应的横坐标，根据IDMM趋势线就可以估计该瞬时频率成分的相位函数。

理论上，ETFR中幅值最大的IDMM趋势线与齿轮转频之间存在固定的比例关系，计算公式如下

(5)

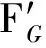
最后，根据式(5)和实际情况下齿轮传动比得到各齿轮啮合频率及其倍频曲线，从而求得各解调函数的相位函数，将每一个解调函数转变为频率恒定的平稳信号，分别采用带通滤波分离出齿轮各阶频率曲线。采用迭代广义解调算法可以削弱齿轮啮合对轴承信号产生的干扰，利用峭度谱自适应的选择由故障轴承引起的高频共振中心，对剩余信号通过自适应选择的滤波中心及带宽进行滤波，就可以提取出最能反应轴承故障特征冲击的滤波信号。

2 基于IDMM重采样的滚动轴承故障诊断

阶次分析是解决变转速轴承故障诊断较为常用的一种方法，可以将时域非周期信号转化为角域平稳信号，角域重采样是按照时域信号相对于参考轴的等角增量方式进行采样。当轴承在变转速模式下运行时，高频共振不仅会对故障特征频率产生调制作用，还会调制较低的转频，调制后的转频会在阶次谱出现一个突出的转频阶比。在齿轮、轴承的混合信号中，通过峰值搜索算法在ETFR中提取的IDMM趋势线表示齿轮啮合幅值最大的倍频，轴承转频与IDMM趋势线存在固定的比例系数，该比值与机械的传动比有关。将IDMM趋势线等效为轴承转频对故障轴承进行角域重采样，将时变的非周期信号转化为角域的周期信号，若轴承发生局部故障，其对应的故障阶比及其倍频峰值将会呈现衰减特性，在轴承阶次谱上呈现的一阶故障特征阶比(Fault Characteristic Order, FCO)与轴承转频阶比(Bearing Rotational Order, BRO)的比值表示故障轴承的特征系数，通过与已知轴承的故障特征系数对比从而得到轴承的故障类型。

迭代广义解调齿轮信号分离的变转速滚动轴承故障诊断步骤如下(故障诊断流程，如图1所示。)

步骤1对原始信号进行Hilbert变换与STFT变换得到ETFR，估计ETFR中齿轮啮合频率及其倍频分量的个数。

步骤2采用峰值搜索算法在ETFR中提取IDMM趋势线，通过式(5)及传动比计算各齿轮啮合频率曲线fk(t)。

步骤3根据待解调信号的瞬时频率曲线构造其相位函数sk(t)

(6)

并得到解析信号y(t)=x(t)+jH[x(t)]，对y(t)进行广义解调后得到频率恒为fk(0)解析滤波分量dk(t)=yk(t)e-2πjsk(t)。

步骤4对解析滤波分量dk(t)进行窄带滤波，中心频率为fk(0)，fwidth为带宽，分离出单分量信号Uk(t)。

步骤5重复步骤3～步骤4，直至分离出所有齿轮啮合频率及其倍频分量信号，剩余信号主要为故障轴承振动信号。

步骤6通过快速谱峭度算法计算轴承共振解调的滤波参数，根据谱峭度最大值所确定的滤波参数进行带通滤波。

步骤7将IDMM趋势线等效为轴承转频，通过式(7)对滤波结果进行角域重采样，得到角域重采样信号，采用阶比谱实现对滚动轴承的故障诊断。

(7)

式中：f(ti)为ti时刻的瞬时转频；N为采样时刻序列号。

图1 本文算法的故障诊断流程图

3 仿真分析

为了验证本文方法的有效性，构造变转速工作模式下故障轴承和正常齿轮混合仿真信号x(t)进行分析。仿真信号x(t)由故障轴承冲击信号、两对正常齿轮振动信号和高斯白噪声n(t)组成

x(t)=xbear(t)+xgear1(t)+xgear2(t)+n(t)

(8)

故障轴承冲击引起的信号xbear(t)的表达式

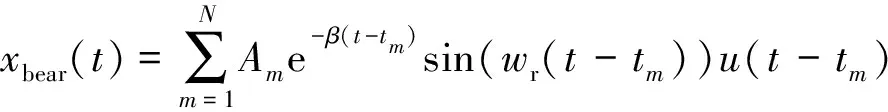
(9)

式中：N为冲击数量；Am为第m个冲击相应的幅值；其冲击幅值随时间线性变化Am=0.8t+1；β为结构衰减系数；μ(t)为单位阶跃函数；wr为轴承故障激发的共振频率；tm表示第m个冲击出现的时间；tm由递推公式(10)确定

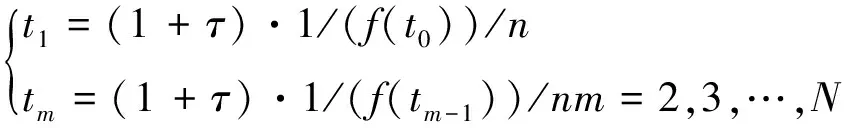
(10)

式中：f(t)为轴承转速；τ代表滚动体的滑移引起的冲击间隔误差，其取值一般为0.01～0.02；n代表轴承每转的冲击数。

正常齿轮振动信号xgear(t)的表达式为

(11)

式中：i(1,2,…,G)为齿轮啮合频率谐波数；Xi为第i阶谐波的幅值；L表示齿轮齿数；齿轮转频fg(t)与轴承转频的关系为fg(t)=τf(t)；Lfg(t)为齿轮啮合频率对时间的变化规律。

对轴承齿轮混合信号仿真时，将轴承转频设置为f(t)=2.5t+25(rps)；两对齿轮的啮合频率峰值、二倍频峰值和三倍频峰值分别设置为0.4、1.2、0.5和0.2、0.9、0.3；齿轮齿数分别设置为L1=24和L2=15；转频比分别设置为τ1=0.8和τ2=0.5。其它具体参数，如表1所示。

表1 仿真信号参数表

图2为仿真信号的时域波形图，图3为添加高斯噪声为5 dB时混合信号的ETFR。从图3可知，轴承信号被齿轮信号掩盖，只能看到两对齿轮的啮合频率及其倍频。原始混合信号的快速谱峭度，如图4所示。其共振中心1 484.4 Hz，在齿轮啮合频率变化范围内，说明齿轮啮合对轴承共振中心的选择产生干扰。

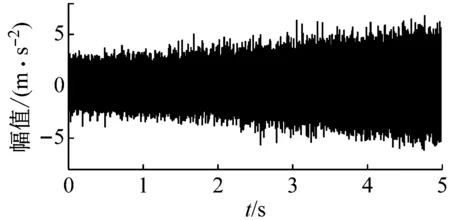
图2 仿真信号的时域波形图

图3 仿真信号ETFR图

图4 未经滤波的谱峭度

采用本文提出的方法对混合信号中齿轮信号进行分离。首先，通过峰值搜索算法从ETFR中提取IDMM趋势线，其中，提取的IDMM趋势线与预先设置的第一对齿轮二倍频峰值最大相吻合，如图5所示。另外，为了验证采用峰值搜索算法提取IDMM趋势线时的抗噪性能，本文分别在添加高斯噪声为0和-5 dB两种强噪声干扰下进行IDMM趋势线提取，其它预设参数不变，从图6和图7可知，在不同噪声干扰下，部分齿轮啮合倍频曲线被噪声掩盖，但最大峰值啮合倍频依然可见，且提取的IDMM趋势线均与预设的第一对齿轮二倍频峰值最大基本吻合，说明峰值搜索算法在提取IDMM趋势线时受噪声干扰影响较小。

图5 预设的IMF和提取的IDMM趋势线

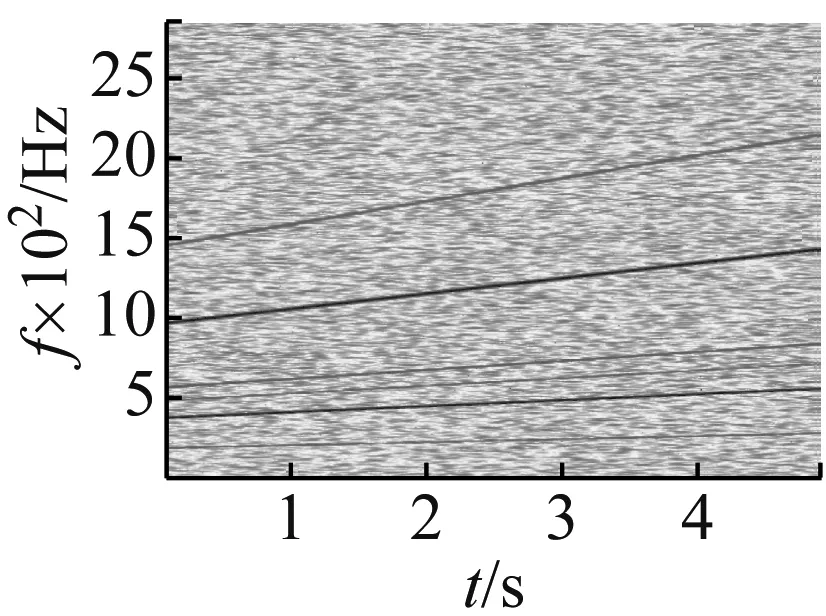
图6 0高斯噪声下的ETFR和IDMM趋势线

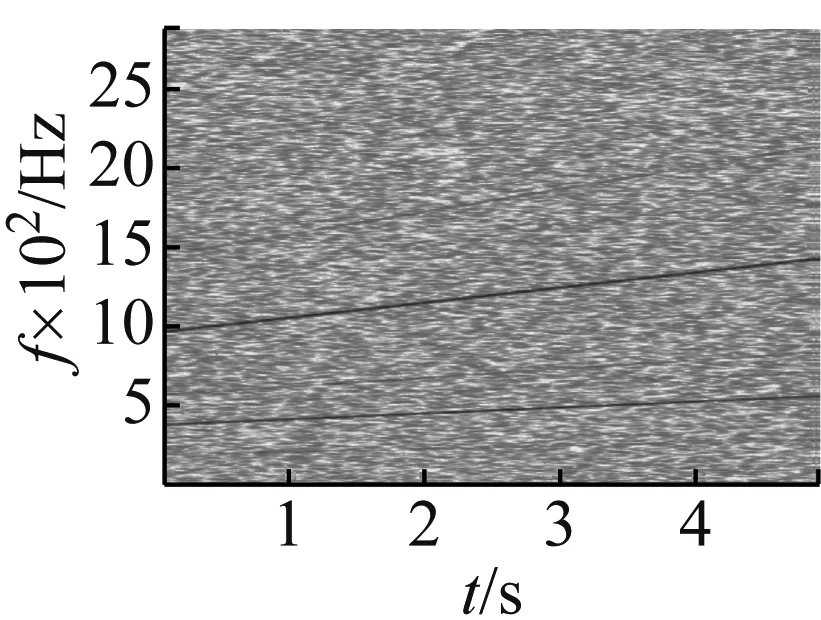
图7 -5 dB高斯噪声下的ETFR和IDMM趋势线

从图3中提取IDMM趋势线后，通过式(5)和预设参数计算其它齿轮啮合频率曲线，构造解调函数的相位函数，并采用IGD(Iterative Generalized Demodulation)算法对齿轮信号进行分离，对剩余信号计算快速谱峭度谱得到共振中心为4 583.3 Hz，与预设轴承共振中心4 500 Hz误差仅为1.85%，根据谱峭度最大所确定自适应滤波参数对剩余信号进行带通滤波，得到最能反映轴承故障信息的滤波信号。最后，将IDMM趋势线等效为轴承转频，对滤波结果进行角域重采样，重采样信号的故障特征阶次谱，如图9所示。在故障特征阶比谱上清楚地看到随阶比衰减的倍频峰值以及轴承转频阶比，前4阶轴承故障阶比对应的横坐标为0.090 82、0.181 6、0.272 5、0.363 3。轴承转频阶比对应的横坐标为0.026，轴承一阶故障特征阶比与转频的特征阶比的比值为3.493，与预设的故障特征系数3.5误差仅为0.2%，从而可以判断轴承发生了故障。以IDMM趋势线对混合信号做重采样所得到故障轴承阶次谱，如图10所示。可以清楚地看到齿轮阶比峰值较大，对轴承阶比峰值产生了干扰，且故障轴承阶比幅值明显变小，几乎难以辨认。因此，本文提出的方法可有效地解决变转速工作模式下齿轮对轴承的干扰影响和精确的识别故障轴承类型。

图8 齿轮分离后的谱峭度

图9 齿轮分离后的故障特征阶比谱

图10 重采样信号的包络谱

4 实测故障轴承验证分析

利用动力传动综合实验台为对象测取变转速工况下故障轴承的振动信号，试验台的结构，如图11所示。由行星齿轮和两级平行齿轮传动系统构成，其中，行星齿轮的个数为3，齿轮箱齿轮参数，如表2所示。信号采集器为NI 9234采集卡，采样频率为25 600 Hz，通过速度控制器改变轴承转频。其中，被监测对象为第二级平行齿轮中间轴上的内圈故障轴承，故障轴承的主要几何参数，见表3。算法结果流程图，如图12所示。

图11 试验台的结构

内圈轴承故障特征系数为

(12)

对变转速工况下故障滚动轴承实测信号进行处理，图12(d)为振动信号的时域波形图，原始信号的快速谱峭度，如图12(f)所示。共振中心频率处于齿轮啮合频率范围内，说明齿轮对轴承的产生了干扰，影响了轴承高频共振中心的获取，因此，采用本文提出的方法对齿轮信号予以分离。原始信号的ETFR，如图12(a)所示。首先，采用峰值搜索算法得到如图12(b)所示的IDMM趋势线，提取的IDMM趋势线与第一级平行齿轮啮合频率的二倍频几乎完全吻合，通过式(5)和齿轮传动比计算其它齿轮啮合频率及其倍频曲线。采用本文提出的迭代广义解调算法对齿轮信号进行分离，图12(c)为提取齿轮信号的ETFR图，清楚的看到分离出了齿轮啮合频率及倍频曲线，与图12(a)中各频率曲线基本吻合。

其次，对剩余信号计算快速谱峭度，计算结果，如图12(e)所示。可看到解调中心为11 733.3 Hz，没有处在齿轮的啮合频率范围内，解调中心变为高频共振区域，说明本文提出的方法有效地削弱了齿轮啮合对轴承的干扰。根据最大峭度值所确定的滤波参数进行带通滤波，得到能够反应轴承故障特征的滤波信号。最后将IDMM趋势线等效为轴承转频对自适应谱峭度滤波结果进行角域重采样，重采样信号，如图12(g)所示。利用傅里叶变化和包络谱得到轴承的阶次谱，从图12(h)可知，随阶比衰减的倍频阶比峰值以及轴承转频阶比峰值，前四阶故障轴承特征阶比所对应的横坐标分别为0.111、0.221 9、0.332 9和0.443 8，转频阶比对应的横坐标为0.020 51，轴承一阶故障特征阶比与转频特征阶比的比值为5.412，与实际内圈故障特征阶比5.43精度误差仅为0.33%。因此，可判断被监测轴承为内圈故障。为验证本文提出方法的优势，对振动信号不采用本文方法处理，将IDMM趋势线等效为轴承转频获得的故障轴承的阶次谱，如图13所示。只可以看到一阶阶比和转频阶比，齿轮干扰峰值较多，轴承的故障类型判断较为困难。因此，综合以上实验分析可得，本文提出的方法可有效地对被监测轴承的故障类型进行判别。