中国消费者信心指数与居民消费价格指数的关系研究

徐国祥，刘 璐

（上海财经大学 统计与管理学院，上海 200433）

0 引言

消费者信心是消费者主观感受和预期的体现，消费者信心指数则是通过量化消费者对当前经济、经济前景、收入、收入预期等感受进而得到的体现消费者信心强弱的一个综合指标。消费者信心指数的编制始于1940年美国的密西根消费者信心指数，1967年又出现了美国国会信心指数。继美国的消费者信心指数的调查编制，其他国家也纷纷编制本国的消费者信心指数。我国由国家统计局负责于1997年12月开始编制中国消费者信心指数，于1999年1月开始公布。

在消费者信心指数的调查编制工作开展后，国内外学者开展了对消费者信心相关的研究，对消费者信心与宏观经济的研究极具价值，国内外对二者间关系的研究较多，本文对分析消费者信心指数与宏观经济关系的文献进行大致梳理后发现，研究中对信心与宏观经济间的影响关系存在不同观点，有部分研究认为信心与宏观经济间存在影响关系，而部分研究认为信心与宏观经济间不存在影响关系。由于消费者信心与我国经济间关系的研究在理论上和应用上都具价值，因此本文将利用由国家统计局发布的中国消费者信心指数，研究其与反映我国通胀情况的居民消费价格指数间的关系，以探究信心与宏观经济间的影响关系。

本文利用交叉谱分析确定消费者信心指数的波动领先于CPI，并测算出具体领先期。由于CPI、CCI间存在非线性关系，本文首次构建MS-VAR模型刻画中国消费者信心指数对居民消费价格指数作用的状态转换和非线性特征，更加深入地理解消费者信心与价格指数间的关系。

1 文献回顾

国外学者对消费者信心研究较早，Kumar等（1995）[1]对比VAR、BVAR模型，发现基于BVAR模型，在经济活动中，消费者信心指数可以作为一个领先指标。Batchelor和Dua（1998）[2]研究发现消费者信心有助于预测1991美国经济衰退，由于经济衰退的特殊性，结论没有推广到其他年份。Desroches和Gosselin（2002）[3]构造了阈值模型研究消费者信心指数对消费支出的预测能力，发现信心在关键时期包含了超过收入所包含的信息。Nadenichek（2007）[4]构造了一个包含可变资本利用率、均衡不确定性的真实商业周期模型模拟日本经济，仅受信心冲击的推动，该模型可复制20世纪80年代后期出现的经济泡沫以及90年代发生的经济持续放缓。Christiansen等（2014）[5]探究美国消费者信心指数是否可助于预测商业周期，发现信心包含不同于其他变量的可预测商业周期的信息。Segers等（2017）[6]运用一种新的数据收集方法衡量每日消费者信心，测算了荷兰消费者信心并发现消费者信心可以更好地预测消费。Dees（2017）[7]运用VAR模型，发现消费者信心对消费以及实际GDP冲击显著，拓展后发现FAVAR模型在消除国家信心冲击的相关性以及阻隔相互正交的特质部分是有效的，信心在经济周期波动中有重要作用。

国内学者对消费者信心与宏观经济的关系研究起步较晚，张道德和俞林（2009）[8]对消费者信心指数、CPI、PMI建立VAR模型分析三个指标间的相关关系，发现PMI对CCI存在正向影响，CPI对CCI有负向影响。陈彦斌和唐诗磊（2009）[9]基于格兰杰因果检验、线性回归模型发现，我国消费者信心对宏观经济影响微弱，而企业家信心可影响宏观经济。赵磊（2010）[10]基于多项式分布滞后模型、格兰杰因果检验，研究了我国消费者信心指数与CPI等经济变量间的关系，发现消费者信心指数可预测CPI、失业率，对CPI有显著的引导作用，对其他变量不存在显著的引导作用。郭洪伟和吴启富（2013）[11]基于VAR模型研究了消费者信心指数及满意度指数、预期指数与物价、消费等关系，发现消费者信心指数可引导消费，其中预期指数可预测未来三个月消费者的消费，CPI影响消费者信心指数存在滞后。张英奎和张帅（2014）[12]通过logistic向量自回归模型研究了消费者信心指数与CPI的关系，发现伴随消费者信心低迷，物价水平也处于低通胀水平。司颖华（2015）[13]通过互谱分析发现CCI领先CPI 0.15个月，运用小波变换发现短、中期CCI与CPI间关系不显著。王岱等（2016）[14]基于VAR、方差分解等方法研究CPI、PMI等对我国消费者信心的影响，发现CPI对消费者信心存在负向影响。孙颖（2016）[15]基于VAR、VEC模型研究了消费者信心指数与居住类CPI的关系，发现二者间存在长期均衡的关系。李成（2016）[16]基于VAR模型发现我国消费者预期指数对PMI未来9个月后的预测能力较大，通过Probit模型发现预期指数也可预测产出。刘伟江和李映桥（2017）[17]通过DCC-GARCH模型研究了网络消费者信心指数与PMI的关系，发现二者间相关性动态时变特征显著，存在较大的波动性，二者间的相关系数持续性较强，通过格兰杰因果检验验证了网络消费者信心对PMI有预测作用，反之不存在影响。

通过文献梳理发现各学者的研究结论并不一致。当前的研究中较多使用格兰杰因果检验、VAR模型研究消费者信心与宏观经济间关系。但是考虑到经济时序的波动复杂情况，VAR模型无法识别经济变量间关系的时变特征。因此本文使用交叉谱分析研究我国消费者信心与居民消费价格指数间的领先滞后关系，并基于MS-VAR模型进一步探究二者间的关系。

2 研究方法

2.1 交叉谱分析

两变量交叉谱分析是通过对二者交叉协方差函数傅里叶变换，选取合适的窗函数平滑处理，进而取得式（1）互谱密度函数：

其中，XC(m)是后延为n的交叉协方差函数，C(w)是谐谱，Q(w)是正交谱，表达式如式（3）和式（4）所示。

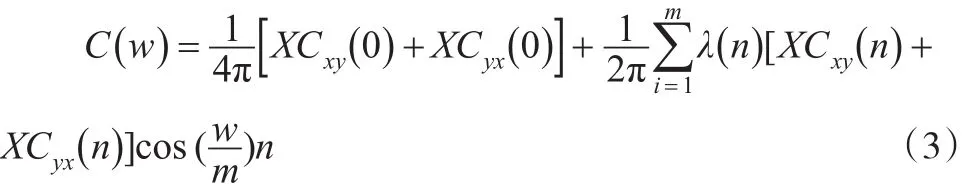
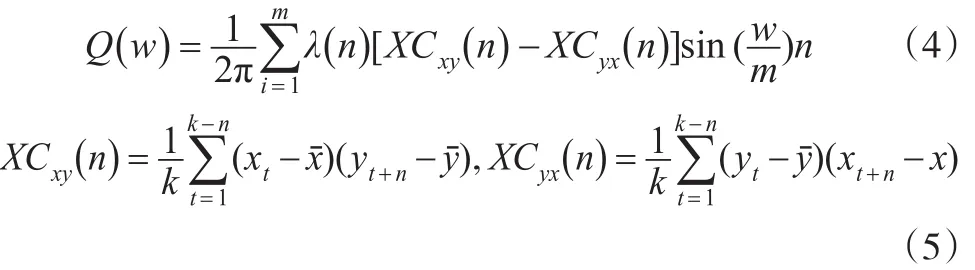
进行交叉谱分析时，描述变量间关联性一般使用振幅（ampl）、相干谱（coh）、相位谱（phase），如式（6）至式（8）所示：

其中，Px，Py分别为在频率w处两变量X、Y序列的谱密度值。

振幅用于描述两个时序间波动程度，振幅越大则波动越剧烈，可更好地解释方差，两时序对某周期行为的共同完成度更高。相干谱即一致性统计量，描述了两时序在频域中的相关性，相干谱取值在0到1之间，该频率下两时序相关性越强则相干谱越接近1。相位谱反映了各频率上两时序间相位差，取值在-π到π间，时差统计量可由相位谱除以频率得到，交叉谱分析中判断两时序的领先滞后关系可由时差统计量的符号判断，其值即是两时序间领先或滞后期数。

2.2 MS-VAR模型

Hamilton（1989）[18]提出单变量的MS-VAR模型，其后Clements和Krolzig（1998）[19]提出多变量MS-VAR模型，相较于假定参数固定的VAR模型，MS-VAR模型可描述不同区制下VAR模型。

考虑如下VAR（p）模型：其中，y是K维时间序列向量，y=(y ，…，y)'，

tt1tKt t=1，…，T,ut～IID(0，∑)。将式（9）表示成如下均值调整后VAR模型：

yt的条件概率密度函数为:

式（11）中，Yt-1是观测值是可观测区制数，st∈{1，…，M}，θm是在区制m（m=1,…M）中VAR模型的参数向量。

在给定的区制st下，构建p阶的VAR模型如下：

假设st服从离散状态马尔科夫随机过程，其转换概率如下：其中piM=1-pi1-…-pi，M-1，i=1，…，M。

其 中 ，ut～NID(0，∑(st))，μ(st),A1(st)，…，Ap(st),∑(st)是描述参数μ,A1，…，Ap,∑在区制st中的依赖性的转换函数参数。

在模型（14）中，在区制变化后过程的均值存在一个立即跃升。这里假设在区制变化后均值平滑地接近新的水平更为合理，即模型中加入一个区制相关的截距项ν(st)，模型如下：

MS-VAR模型的一般表现形式中，自回归的所有参数均与服从马尔科夫链的状态st相关，模型如下：

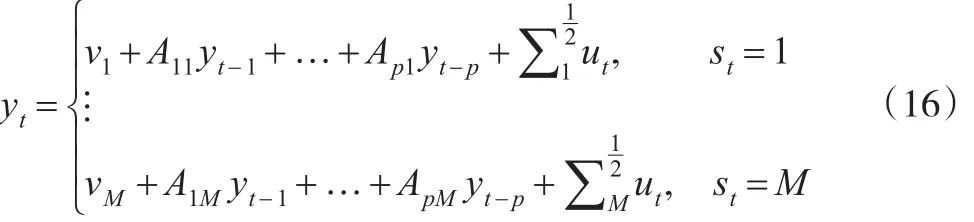
其中，ut～NID(0，IK)。

鉴于MS-VAR模型有多种形式，为了区分不同模型，Krolzig给出MS(M)每种模型区制相关参数的表示：M表示马尔科夫转换的均值，I表示马尔科夫转换截距项，A表示马尔科夫转换自回归参数，H表示马尔科夫转换异方差。

3 消费者信心与居民消费价格指数关系

3.1 样本数据描述

作为宏观经济运行的核心指标，居民消费价格指数代表下游消费价格，可衡量通胀情况。居民消费价格指数（同比）来自中经网的同比月度数据，文中用CPI表示。本文中中国消费者信心指数来自中经网的月度数据，用CCI表示。以上所有数据时间为1999年1月至2018年4月。

图1 消费者信心指数、居民消费价格指数走势图

如图1所示，CCI、CPI原始序列趋势图，1999年1月至2003年2月，CCI值在110附近平稳波动，其后骤降，至2003年5月为100后回升，2003年6月至2016年8月期间在105附近上下波动，在2011年11月达到样本期间最低值97,2016年9月后呈上升趋势。由图1可见，在2008年前中国消费者信心指数的数值比2008—2017年的平均水平稍高。这除了与物价等有关外，还与2007年10月后长达一年的中国股市暴跌、2011年前后出现的欧债危机、2013年的“钱荒”事件、2015年底至2016年初的A股股灾有关，这些不利因素的产生，使得这期间消费者的信心不足。分析CPI的走势，在1999—2013年期间，CPI的走势起伏较大，1999年4月达到样本期间最小值97.8，在2008年4月达到样本期间最大值108.5。2013年后，CPI波动较平稳，在102附近上下波动。直观上可以看出CCI的波动趋势领先于CPI。

3.2 数据预处理与平稳性检验

通过上文的描述性分析可知，直观上可看出CCI在样本期间不同时期状态特征有区别，且CCI对CPI有领先趋势。精确地测度CCI对CPI的领先期数并分析CCI的不同时期状态特征下其与CPI间的关系对物价的稳定以及相关政策制定有着重要意义。本文首先采用交叉谱分析方法对CCI与CPI间的领先滞后关系进行分析，然后使用MS-VAR模型探究CCI、CPI间的关系。

由于交叉谱分析方法、MS-VAR模型均对数据有平稳性要求，CCI、CPI原始序列不平稳，对CCI、CPI原始序列数据进行如下预处理：首先使用X12对CCI、CPI进行季节调整，再使用参数为14400的H-P滤波法对经季节调整后CCI、CPI进行处理得到周期项序列，分别记为CCIcycle、CPIcycle。本文对CCIcycle、CPIcycle进行平稳性检验，检验结果如表1所示，可见CCIcycle、CPIcycle均平稳。

表1 平稳性检验

对CCIcycle和CPIcycle进行格兰杰因果检验，结果如表2所示，在10%的显著性水平下，CPIcycle不是CCIcycle的格兰杰原因，CCIcycle是CPIcycle的格兰杰原因，即消费者信心指数对居民消费价格指数有显著影响，反之影响不显著。

表2 格兰杰因果检验结果

3.3 交叉谱分析

对CCIcycle、CPIcycle做交叉谱分析，当耦合振荡周期为38.67个月时，CCIcycle与CPIcycle的振幅最大值为15.36，CCIcycle的波动趋势领先CPIcycle3.11个月。通过交叉谱分析得到，消费者信心指数的变动趋势领先于居民消费价格指数3.11个月，可见，消费者信心指数对居民消费价格指数有一定的预测能力，可作为宏观经济运行的先行指标。

表3 交叉谱分析结果

在验证了消费者信心指数对宏观经济有预测作用后，本文进一步使用MS-VAR模型探究CCI、CPI在不同时期的状态特征下间的关系。

3.4 MS-VAR模型

在使用MS-VAR模型进行计算前，本文首先通过BDS检验以检验居民消费价格指数与消费者信心指数间是否存在非线性的关系。本文首先建立CCIcycle、CPIcycle的二元VAR模型，根据AIC、SC、HQ等准则以及对数似然估计值，对CCIcycle、CPIcycle的无约束VAR判断最优滞后阶数为1，然后对建立的VAR(1)的残差进行BDS检验判断CPI和CCI间是否存在非线性关系，BDS检验结果见表4所示。

表4 居民消费价格指数与消费者信心指数间非线性关系检验结果

通过表4可见，CPIcycle和CCIcycle的VAR(1)模型残差的BDS统计量，在5%的显著性水平下均拒绝独立同分布的原假设，即可认为CPIcycle与CCIcycle间存在非线性关系。

基于上述非线性关系的确定，接下来本文建立区制数量为2区制，即高信心和低信心，滞后阶数为1的MS(M)-VAR(1)模型，并依据AIC、SC、HQ准则和对数似然估计值，对模型进行比较，最终建立MSIH(2)-VAR(1)模型。MSIH(2)-VAR(1)通过模型显著性检验，模型估计结果如表5所示。

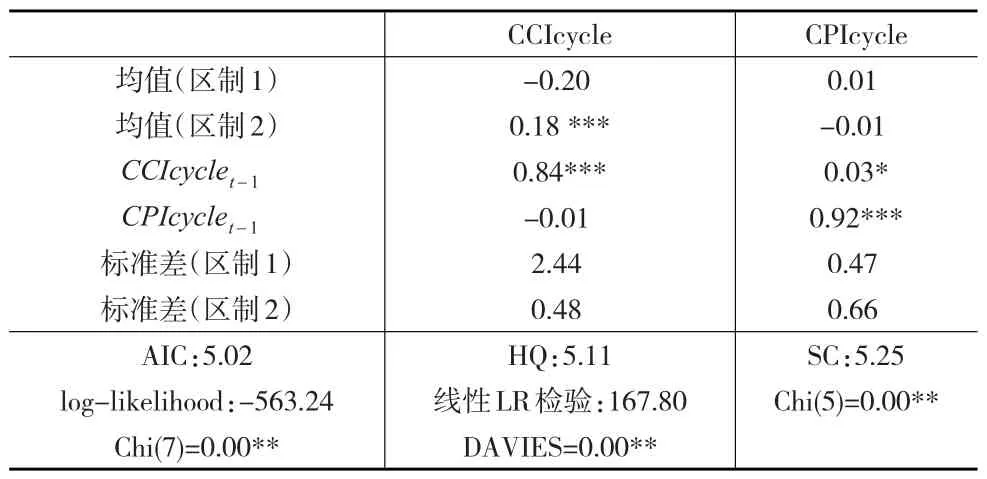
表5 MSIH(2)-VAR(1)估计结果

从CCI方程看，滞后1期的CPI波动对CCI有负向作用，即当居民消费价格指数上升，会导致消费者信心下降。从CPI方程看，滞后1期的CCI波动对CPI是正向影响，即消费者信心增强，会导致居民消费价格指数上升。

图2所示两区制转换概率图，结合表6所示区制属性，可见，区制1（低信心）对应2003年4月至2003年8月、2004年5月至2004年8月、2007年3月至2007年4月、2008年11月至2009年1月 、2009年3月至2009年6月 、2010年3月至2016年12月、2017年8月至2017年12月。区制2（高信心）对应1999年2月至2003年3月、2003年9月至2004年4月、2004年9月至2007年2月、2007年5月至2008年10月、2009年2月、2009年7月至2010年2月、2017年1月至2017年7月。自1999年1月以来存在13次区制转换，时点分别在2003年3月、2003年8月、2004年4月、2004年8月、2007年2月、2007年4月、2008年10月、2009年1月、2009年2月、2009年6月、2010年2月、2016年12月、2017年7月。在1999年1月至2018年4月间，我国消费者信心处于低信心时期的频率为45.31%，处于高信心时期的频率为54.69%，处于区制1（低信心）的持续期稍短于处于区制2（高信心）的持续期。从模型估计的区制转移概率阵可知，在区制1（低信心）时期，维持原状态的概率为0.89，由区制1（低信心）向区制2（高信心）时期转移的概率为0.11，进入区制2（高信心）后维持原状的概率为0.09，由区制2（高信心）向区制1（低信心）转移的概率为0.91。从区制转移概率阵可见，区制具有较强的稳定性，在未受外部冲击下进行区制转换的概率较低。与前文描述性分析相吻合，可见两区制下MS-VAR模型的分析结果较为符合实际情况。

图2 两区制转换概率图

表6 区制属性

图3 脉冲响应图

通过分区制无累积效应的正交脉冲响应图3（见下页）可知，在低信心的区制1下，给CCI一个正向冲击，CPI会增加，在第6期附近脉冲效应达到最大，其后逐渐消减。在区制1下，给CPI一个正向冲击，CCI受到负向影响，在第8期附近负向脉冲效应达到最大，其后逐渐消失。在高信心的区制2下，给CCI一个正向冲击，CPI会增加，在第5期附近脉冲效应达到最大，其后消减。在区制2下，给CPI一个正向冲击，CCI受到的负向影响在第8期附近脉冲效应达到负向最大，其后逐渐消失。从CCI的角度来看，CPI上升对CCI产生负向影响，即使CCI出现下降趋势，而CCI的下降会使CPI出现下降；从CPI的角度看，CCI的上升会对CPI产生正向影响，即CPI出现上升趋势，而CPI上升会使CCI出现下降。

4 结论与建议

4.1 结论

本文选取1999年1月至2018年4月的中国消费者信心指数与居民消费价格指数月度数据，首先对中国消费者信心指数与居民消费价格指数进行格兰杰因果检验，继而进行交叉谱分析测度二者间领先滞后期，最后通过MS-VAR模型探究了二者间的关系，得到如下结论：

第一，通过对中国消费者信心指数与居民消费价格指数进行格兰杰因果检验发现，在10%的显著性水平下，CPI不是CCI的格兰杰原因，CCI是CPI的格兰杰原因。可见中国消费者信心指数对居民消费价格指数有显著影响，而居民消费价格指数对中国消费者信心指数无显著影响。

第二，对中国消费者信心指数与居民消费价格指数进行交叉谱分析结果看，CCI领先CPI 3.11个月。CCI与CPI的耦合振荡周期是38.67个月时振幅最大为15.36，CCI与CPI周期项的相干谱为1，这说明CCI与CPI的波动在耦合震荡周期时相关性较强。可见，CCI对CPI有一定的预测能力，可作为宏观经济运行的先行指标。

第三，通过对中国消费者信心指数与居民消费价格指数建立MSIH(2)-VAR(1)模型，在1999年1月至2018年4月期间，可以划分为两个区制，区制1表示信心相对低水平时期，区制2表示信心高水平时期，处于区制2的时期稍长于处于区制1的时期。通过MSIH(2)-VAR(1)模型估计结果发现滞后1期的CPI对CCI有负向作用，影响不显著；滞后1期的CCI对CPI有显著的正向影响。通过脉冲响应分析发现，在不同区制下，CPI对CCI的冲击呈负向，CCI对CPI的冲击均是正向，说明二者间存在长期均衡的关系。

4.2 对策建议

第一，消费者信心作为经济运行的先行指标，可通过消费者信心指数预测通胀。中国消费者信心指数对居民消费价格指数有一定的预测作用，消费者信心领先于CPI 3.11个月，可通过消费者信心预测通胀进而合理定制调控政策。

第二，在消费者信心处于稍低水平时期，可通过对物价进行调控进而使消费者提高信心。由于消费者信心与居民价格指数间存在长期均衡关系，在两区制中低信心状态下，消费者信心与物价间相关性强于高信心状态下的相关性，所以在低信心状态下，对物价调控可提高消费者信心，由于二者间存在一个循环传导路径，因而会对物价产生影响，形成一个循环。

第三，防控系统性风险，加强监管和制度建设，稳定消费者信心。通过分析，低信心状态下的时间与我国股市暴跌、欧债危机等事件发生时间一致，需加强各领域的风险防范措施，经济、信心间反馈调节机制使得经济、信心间维持正常或较好的水平。