物流企业供应链违约风险度量

马 波

（内蒙古大学 法学院，呼和浩特 010010）

0 引言

物流是近年来新型发展的产业，随着国民生活水平的提高，物流产业的发展越来越快，其披露的市场问题也越来越多。由于物流产业的发展年限较少，所以我国在物流信用管理方面的制度还不完善，这样给物流服务交易双方带来了巨大的违约风险。物流的违约风险主要包括两方面：一是风险识别，二是风险度量。然而物流运输过程的影响因素难以准确的获取，所以对物流企业供应链违约风险的预估存在不稳定性。物流供应链的基础为：物流供应商—物流服务商—物流用户，通过提供灵活的物流服务，确保产品通过该供应链正常运输。因此合理构建违约风险度量模型对识别风险、预防风险具有重要意义。

本文选取A物流企业作为实证研究对象，并运用结构模型构建了物流企业供应链违约风险度量模型，系统地分析物流企业供应链违约风险形成机制、影响因素和风险措施。结果表明：构建企业物流风险识别与度量模型时应考虑违约相关性的影响，最终指出应选择恰当的违约风险控制和防范措施，将违约风险降至最低，降低企业总体损失。

1 物流风险识别与度量模型构建

1.1 结构方程模型

结构方程模型又被定义为潜变量模型，潜变量模型指以理论和经验作为基础构建因果关系的假设模型。通过假设模型的理论框架创建可变数据，再比较数据的理论协方差和实际协方差对数据的合理性及正确性进行检验，并尝试检验过程最小化。实际上，这是一种基于传统理论的分析方法，利用路径分析和因子分析的统计分析方法对数据变量进行整合并利用。结构方程模型通过路径分析法将观测变量、潜在变量以及潜在变量与潜在变量之间的影响关系反映出来。学者廖颖林认为结构方程模型的组成因素分别为：潜变量、观测变量、潜变量与潜变量之间的路径、潜变量与观测变量之间的路径、测量模型与结构模型。关于上述几种因素的具体解释说明如下：

潜在变量：又被称为隐变量，指必须通过指标测量而不能直接得到的变量。例如学生的逻辑思维能力，由于其是一个不能直接衡量的变量，因此可以设计数学成绩这一指标进行间接测量。潜变量包括外生潜变量和内生潜变量两种，外生潜变量指对模型中的变量进行解释，其只会影响其他变量，不会被其他变量影响；内生潜变量指在模型中受到其他变量影响的变量。

观测变量：又称显变量。例如学生的成绩，其中可以直接将某一学科的综合得分作为观测变量。

（1）测量模型

测量模型反映了观测变量与潜在变量之间的关系。在测量模型中，观测变量是指标，潜在变量是影响指标的因子，因此测量模型也可称为因子模型。方程（1）和方程（2）即为模型的表现方式：

其中，X代表ξ的观测指标；δ代表X的测量误差；∧x是(q×n)的系数矩阵；代表η的观测指标；ε代表Y的测量误差；∧y是(p×m)的系数矩阵；P代表X的变量数；q代表Y的变量数。

假设E(η)=0,E(ξ)=0,E(ε)=0,E(δ)=0,那么ξ与δ无关,η与ε无关。

在结构方程模型中，利用测量模型对变量因素进行分析，其中包含收敛有效性和判别有效性。即对假设模型的内在模型适配度进行验证。

（2）结构模型

结构模型即因果模型，研究观测变量与潜在变量之间的因果关系，该方程则被称为结构方程。方程（3）即为模型的表现方式：

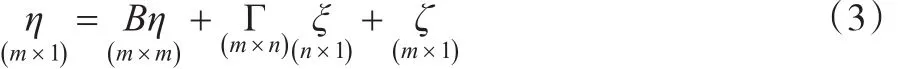
其中，内生潜变量用η来表示；外生潜变量用ξ来表示；随机干扰项用ς来表示；B代表η的系数矩阵；Γ代表ξ的系数矩阵；m代表η的变量数；n代表ξ的变量数。

结构方程模型是因果模型与因子模型的组合式，由此，可以得出模型的方程式：

多个测量模型与一个结果模型都包含在结构方程模型里。要构建结构方程模型必须需要遵循以下几点原则：（1）解释客观现象要强而有力；（2）理论必须得到验证，只有验证过的理论才具有科学特性，才能纠正可能发生的错误；（3）理论必须是简单的，在现有的解释层面上，可以把概念和关系放在更少的理论现象中进行理解。

1.2 模型的构建

（1）参数估计

参数的实际总体协方差与模型拟合协方差的接近程度可以用拟合函数表示，即F=(S， ∑(θ) )。运用不同的参数估计方法，协方差接近程度的拟合函数也不同，使用最广泛的参数估计法为最大似然估计和广义最小二乘估计，其拟合函数为：

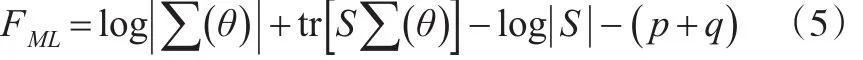
其中，tr[S∑ (θ) ]代表矩阵的对角线元素之和；log| ∑(θ) |代表矩阵 ∑(θ)的行列式对数；log|S|代表矩阵S的行列式对数；p代表内生可测变量的数目；q代表外生可测变量的数目。

（2）模型识别

进行模型识别可以确保自由参数能够从观测数据中获取估计值。这是因为当自由参数无法从观测数据中获取估计值，则改模型无法识别，当自由参数可以从观测数据中获取估计值，则模型可识别。模型的正确识别和过度识别取决于对自由参数、固定参数和限制参数这三种参数的选择。其中，自由参数属于未知的参数，需要预计；固定参数受到一系列因素的限制，如果路径系数之间的潜在变量为0，潜在变量和可测变量之间的因子载荷就为1；限制参数与自由参数一样，属于未知参数。利用参数固定或限制，可以降低自由数，也可轻易识别模型。在构建初始模型时，可利用此方法进行模型识别与预测，再经过检验、修改、调整、选择，最终成立模型。

模型识别分为两个部分：第一部分，判断反映潜变量与观测变量之间关系的测量模型是否可以被识别；第二部分，判断反映潜变量与观测变量之间因果关系的结构模型是否可以被识别。

步骤一：测量模型识别公式。

识别判定的三指标规则：两列的载荷矩阵至少必须有三个非零元素；载荷矩阵中的每一行只能够有一个非零元素；误差是无关紧要的，即协方差矩阵的误差。

步骤二：结构模型识别。

结构模型为：

在对本文模型进行识别判断时，只有当第一部分识别符合后才需要进行第二步识别。当两次模型识别的结果都符合，则整体的模型是可以使用的。但是存在一些结构方程可以进行实际应用但是不满足进行两步识别，因此两步识别法不是判断模型的必要条件。

2 确定风险评估指标

物流企业违约风险分为非主动性违约风险和主动性违约风险。非主动性违约是指由于暴雨、暴雪、地震等不可控因素造成运输物品损坏或丢失；主动性违约是指物流企业虚假承诺企业实际达不到的送货时间，例如企业的服务水平、信用管理等可控因素。本文综合不可控因素和可控因素，建立了物流企业风险指标的评估体系，并对其进行了详细的分类说明，具体如表1所示。

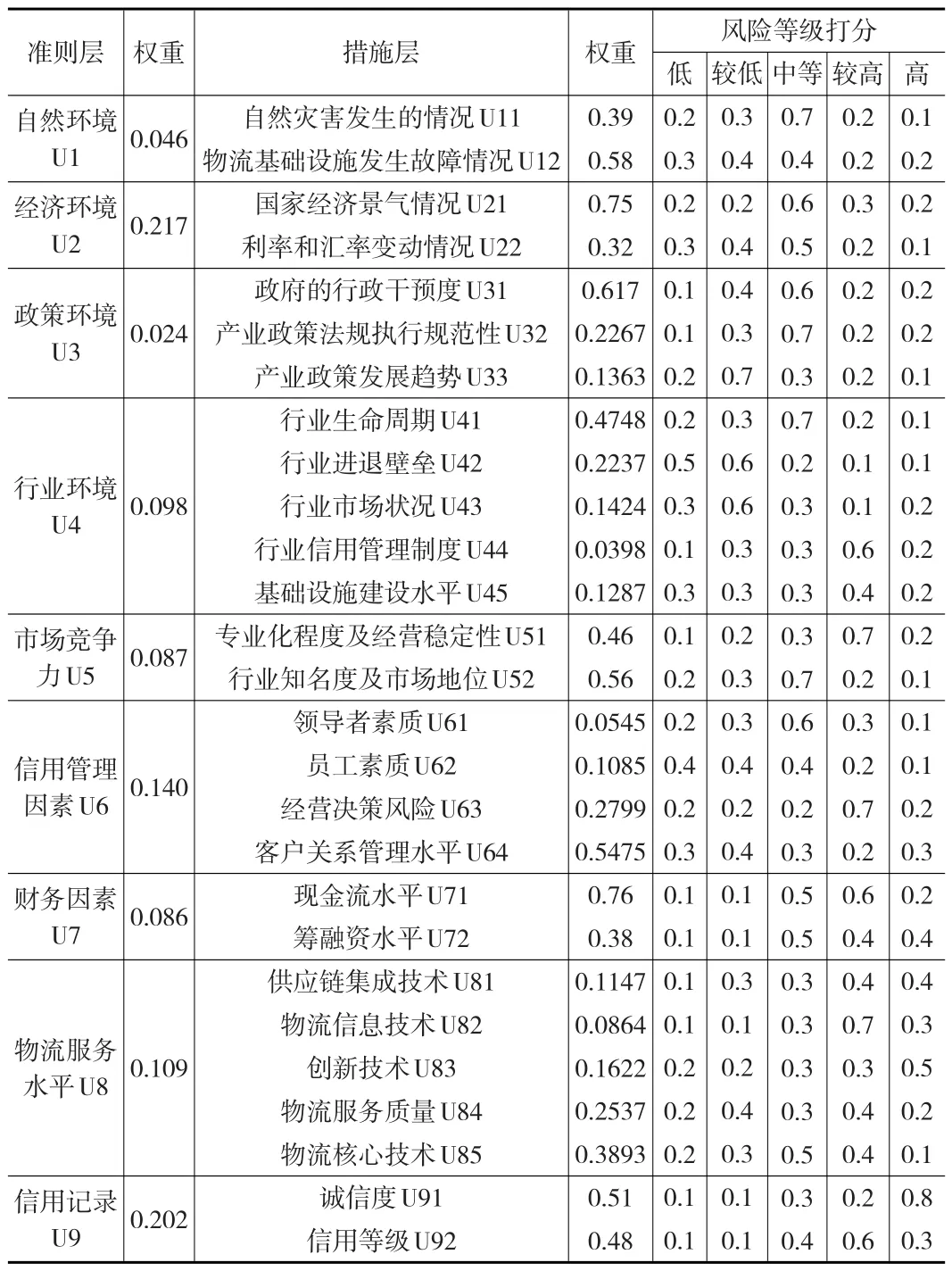
表1 A物流企业各评价指标的权重及风险等级

3 实证分析

本文评估体系的建立，是采访了物流企业信用管理方面的十位专家进行了关于物流企业面临的违约风险问题的问卷调查。其中有三位专家在社区存在一定影响力，并且对市场和物流有所研究，有三位与第三方物流公司关系相对较近，还有两位是物流企业的管理者，最后两位是物流企业的部门经理。运用区间判断矩阵的权重确定法计算各位专家所作评价的指标权重，即表1所得的评估体系。运用数据统计的方法计算专家对物流违约风险影响因素打分的权重值，得出矩阵A，在此基础上对判断矩阵进行修正，最终得出数字判断矩阵B：

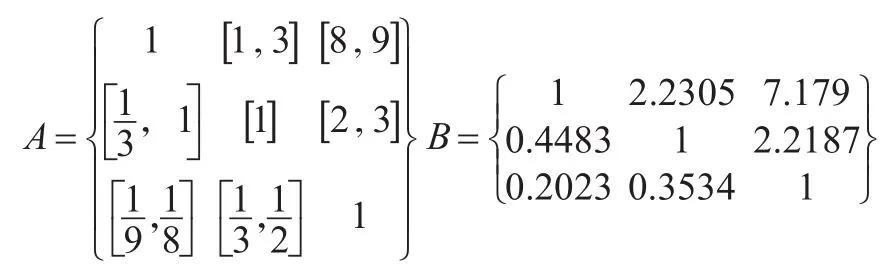
将数据判断矩阵的结果构成准则层矩阵R：

根据矩阵R可以计算出物流企业违约风险评价的模糊综合评判结果为：E=WR=[0.09090.14590.3464 0.2473 0.1667]。从评判结果可以看出本文中的物流企业供应链的违约风险等级为中等。可知物流企业必须选择恰当的防范措施控制物流违约风险，将风险降至最低，进而降低企业总体损失与违约风险。

4 总结

本文将物流企业供应链作为研究对象，构建合理的物流风险识别与度量模型，以违约关联作为主线，系统地分析物流企业供应链违约风险的形成机制、影响因素和风险措施。

（1）目前，我国关于物流企业违约风险的研究，在研究视角和内容体系方面尚不完善，尤其是现在的物流企业风险管理制度对实际市场的适应度不高，无法满足我国市场对物流企业供应链风险管理的需求。

（2）一般在构建风险识别与度量模型时应当考虑违约相关性的影响，因为物流相关企业之间的违约相关性会增加物流服务供应链的违约风险。其中违约相关性涉及两个层次的意义：一是受到共同的外部环境因素的影响，会导致企业之间的间接违规相关性；二是企业之间存在业务往来、借贷等直接关系，从而违约风险有可能传播到附属企业，使附属企业违约概率增加甚至产生违约。

（3）从本文的实证结果来看，形成物流企业供应链违约风险的主要原因有外部环境因素、内部环境因素、成员特征因素以及违约传染因素四个方面。

（4）物流供应链违约风险的严重性在于，任一成员违约会导致其他成员甚至整个物流服务供应链发生中断。物流企业供应链违约风险具有概率性、传染性、人为性以及可控性的特征，因此，应当针对物流业的行业特性，构建风险识别与度量模型，分析违约风险的形成机制、传染机制和控制措施，并选择恰当的违约风险控制和防范措施，将风险降至最低，降低企业总体损失。