射电天文图像的反卷积算法研究∗

张 利 徐 龙 米立功 马家君

(1 贵州大学大数据与信息工程学院贵阳550025)

(2 中国科学院太阳活动重点实验室北京100012)

(3 黔南民族师范学院物理与电子科学学院都匀558000)

1 引言

射电干涉测量通过若干小口径望远镜实现大口径分辨率,并且在天空亮度分布的空间频率域进行采样[1].由于干涉阵的天线数量有限,所以仅部分空间频率被采样,这使得望远镜的点扩展函数(也称为脏束,dirty beam)具有不可忽略的旁瓣.这些旁瓣使得测量图像模糊,从而限制成图的动态范围.

在连续且完全采样的情况下,由van Cittert-Zernike理论[1]可知,真实的天空亮度分布Itrue(x,y)与可见度函数(visibility)Vtrue(u,v)是一个傅里叶变换对,即

其中j为虚数单位.然而实际测量是离散且不完全的,即对天空亮度分布的傅里叶空间进行了不完全采样,且存在噪声Vnoise(u,v).测量的可见度函数Vmeasure(u,v)可表示为

其中S(u,v)为傅里叶空间采样函数,采样点上的值为1,非采样点上的值为0.通常定义脏图(dirty image)Idirty(x,y)、点扩展函数B(x,y)分别为

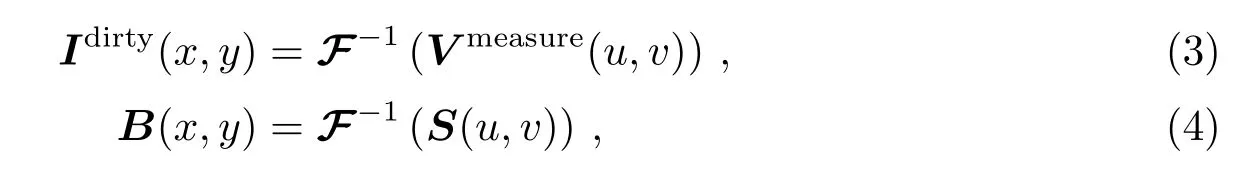
其中F−1表示傅里叶反变换.由卷积理论可知,傅里叶空间的乘积等价于像空间的卷积.则有

其中⋆表示卷积运算,Inoise(x,y)=F−1(S(u,v)Vnoise(u,v)).因此,脏图是设备点扩展函数与天空亮度分布的卷积,同时包含噪声的影响.点扩展函数B(x,y)的旁瓣使得图像模糊.反卷积的目的是去除旁瓣的影响,使图像细节变得更加清晰.

在射电综合成图领域里,大致有3类反卷积:CLEAN算法[2],最大熵MEM算法[3−4]和压缩感知算法[5−6].然而,CLEAN算法是最常用的,在射电干涉图像处理软件中是一个标准的组件.在1974年,由Högbom提出的CLEAN算法[2]的主要目的是为了去除点扩展函数的旁瓣影响.后来很多学者在不同的应用场景下对算法进行了改进.比较有代表性的是Clark CLEAN[7],S-C CLEAN[8],多尺度CLEAN[9−10]和自适应尺度像素分解算法(Asp CLEAN)[11−13].Clark CLEAN算法使用了快速傅里叶变换和截断的点扩展函数,加速了反卷积过程.在S-C CLEAN算法之前,CLEAN算法仅在像空间进行反卷积,Schwab和Cotton将CLEAN算法扩展到傅里叶空间,这种改进有利于减少反卷积过程中的误差累积[8].大多数的CLEAN算法将天空亮度分布分解为一系列delta函数.对于分开较好的致密源,这些方法的性能非常好,但是如果处理延展源,重建的图像通常会带有伪影(artefacts).为解决这个问题,Cornwell[9]在CLEAN算法中引入多尺度基函数.将天空亮度分布分解成一系列尺度基函数,这些基函数的尺度也包括0,即包括delta函数.所以多尺度CLEAN算法对于致密源和延展源均有效.然而,尺度的大小需要用户指定且尺度数目受限于计算机内存.为解决这个问题,Bhatnagar和Cornwell提出了自适应尺度像素分解算法[11].这种算法通过拟合来实现基函数尺度的自适应,从而能够重建出更高质量的图像.但这种算法使用了有效集的优化方式[11],使得反卷积的时间很长.文献[12]通过引入解析高斯反卷积对这个算法进行了优化和加速.这种改进方法在反卷积过程中需要将带有旁瓣的点扩展函数逼近成一个高斯函数,所以仅适用于点扩展函数旁瓣较小的情形.针对这些问题,本文提出一种基于尺度基函数的CLEAN算法.

2 基于尺度基函数的反卷积算法

在CLEAN类反卷积算法中,每次迭代通过找到最可能的真实分量来不断地逼近真实的天空亮度分布.在本文算法中,通过一系列高斯基函数来逼近天空亮度分布,

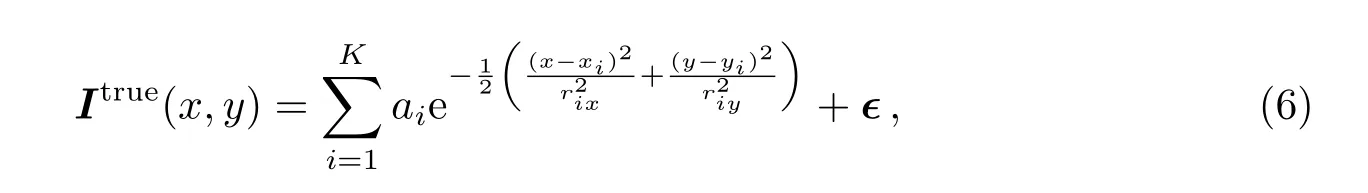
其中K为组成天空亮度分布的分量数目,ϵ为逼近的天空亮度分布和原始天空亮度分布之间的误差,ai为第i个分量的幅度,(xi,yi)为第i个分量的中心位置,(rix,riy)为第i个分量的x和y方向的宽度.本算法采用如下方法找到各个最优分量.

(1)找到初始的参数(αi0,xi0,yi0,rix0,riy0).首先使用几个高斯函数平滑残差图像(第1次迭代时是脏图),然后从前一步得到的平滑残差图像中找到全局极大值,将其对应的高斯函数的宽度作为高斯分量的宽度(半高全宽).

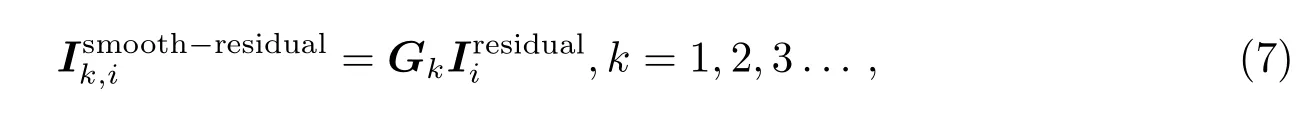
其中,Gk为1个Toeplitz矩阵,每行元素组成1维形式的高斯函数,下一行是通过循环位移上一行的一个元素得到的,k是平滑的残差图像的数量,是第i次迭代的残差图像.

平滑时一般选取4个高斯函数即可.如果数目太少,则无法找到好的初始值.如果数目太多,会显著增加计算量.另外,为了使描述更加简洁,在表示图像的符号中,带坐标的表示图像矩阵,如(x,y);不带坐标的表示图像向量,如.两者表示相同的图像,只是表示不同.

(2)通过Levenberg-Marquardt最小化算法[14]优化初始分量参数来获得最优分量参数(αi,xi,yi,rix,riy).在这里,需要最小化目标函数

其中为第i个高斯分量.

(3)更新模型.在计算最优分量时,对高斯宽度乘以循环增益g.然后将最优分量加入到模型图像中.

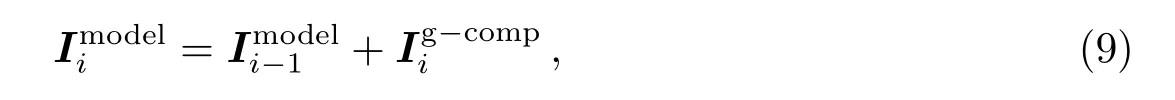
其中为高斯宽度乘以循环增益g后的分量.循环增益可以优化模型分量,防止过分估计,实现更好的重建.正如其他CLEAN算法一样,需要用户指定其大小.对于尺度敏感CLEAN算法,一般g<0.5.

(4)计算残差.

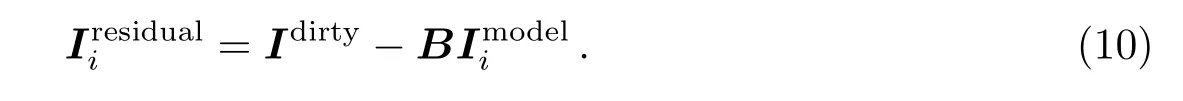
重复上面步骤,直到最大迭代次数或噪声水平时停止.正如其他CLEAN算法一样,最后的重建图像ICLEAN等于洁束(CLEAN beam,通常是高斯函数)与模型图像Imodel的卷积与残差Iresidual之和,即

其中Imodel,Iresidual分别是最后的模型图像和残差图像.BCLEAN是一个Toeplitz矩阵,其行元素由洁束的离散值组成.

在初始参数计算阶段,需要通过平滑当前残差图像来找到一个合适的初始参数.在自适应尺度像素分解算法[11]中,这种平滑通过卷积实现,是一个比较耗时的部分.在本文的算法中,当分量尺度较大时使用卷积平滑的方式来找到初始参数,当分量尺度较小时直接使用残差图像中绝对值最大的点作为初始位置参数和幅度参数,并使用点扩展函数主瓣宽度作为初始宽度参数.本算法中,当最近连续10次的分量宽度平均值在x和y方向同时小于点扩展函数的主瓣宽度时,即

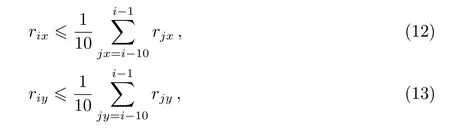
下一次计算初始参数时,适用分量尺度较小的方法.实验证明它能够有效地估计较小的初始分量,从而避免更多的计算量.在测试中发现,在反卷积过程中,小尺度的分量占据较大比例,这种方法加速了反卷积过程.在本算法中,首先找到初始的分量参数,然后通过拟合的方式对初始参数进行优化.在自适应尺度像素分解算法[11]中,使用有效集的方式来实现分量的更好拟合.尽管只有少部分的分量在有效集中,然而参数的成倍增加使得拟合时间大大增加,同时也增加拟合失败的风险.在本文算法中,并不是使用有效集的方式,即前面的分量不被再次拟合优化.每次拟合参数并不增加,这显著加速了反卷积过程.本质上,文献[11]追求搜索空间的正交化,从而实现对源更加稀疏的表示.然而这需要付出更大的时间代价.本文算法并未追求搜索空间的正交化,同时使用新的拟合参数计算方法.两者同时使得本文算法的速度明显提升.在文献[12]中,反卷积过程中点扩展函数是被近似成一个高斯函数,这会导致分量估计不准确.当点扩展函数的旁瓣水平越高时,分量估计误差越明显.然而本文的方法使用完整的点扩展函数来进行反卷积,所以分量估计更加准确.Levenberg-Marquardt算法结合了高斯-牛顿算法和梯度下降算法,具有鲁棒的性能,有利于分量的准确拟合.

CLEAN类算法通过迭代方法求解线性等式系统[15−16],文献[1,15]已经很好地证明了CLEAN类算法的收敛性,其收敛条件为:(1)点扩展函数B(矩阵形式下)必须是对称的;(2)B必须是正定或半正定的;(3)脏图Idirty必须在B的值域(range)内.本文算法使用了不同的分量提取方法,但算法的结构与CLEAN算法相同,同时保持了CLEAN算法的最速下降思想,因此文献[15]的收敛证明适用于本文算法.具体细节请参考文献[15].

3 算法实验

本文利用天文通用软件包(Common Astronomy Software Applications,CASA)和Python语言实现了上述算法.为了测试算法的反卷积性能和避免其他因素影响反卷积的测试效果,我们使用CASA模拟The Karl G.Jansky Very Large Array(JVLA)B阵型对图像M51(如图1(a))进行观测,获得模拟观测数据.观测波段为L波段,1 GHz带宽和32个通道.我们将模拟的可见度函数加入高斯噪声,使得脏图(图1(b))中噪声的均方根误差为5×10−5Jy.在测试中,使用鲁棒加权对测量数据进行栅格化.图1和图2中的单位均为央斯基每像素(Jy/pixel).从图中可以看出,脏图中天体的细节变得模糊不清.图1(c)为本文算法从脏图中重建的图像,可以看出已经很好地重建出原始图像中细节,包括致密源和延展源.图2(a0)和(a1)分别显示了Högbom CLEAN(Hg-Clean)算法[2]的模型图像和残差图像,可以看出该算法对延展结构的表示不佳和残差图像中有明显延展信号.这源于delta函数无法很好地逼近延展结构.从图2可以看出,多尺度CLEAN(Ms-Clean)算法[9]的结果优于Hg-Clean算法的结果.这是因为多尺度CLEAN算法使用尺度基函数来逼近潜在的真实图像.然而它的尺度数量是有限的,一些延展结构不可避免地被分解成预先设定的尺度.自适应尺度像素分解算法[11]很好地解决了尺度的自适应的问题,相对于多尺度CLEAN算法具有更好的性能.图2(d1)显示的是残差图像,可以看出残差图像中没有明显的信号,说明本文算法能够很好地分离源和噪声.这得益于Levenberg-Marquardt算法很好的拟合性能.同时从图2可以看出,自适应尺度像素分解算法[11]的重建结果与本文算法类似,但是从表1和表2可以发现本文算法的速度更快.在测试中,我们发现循环增益使用0.2–0.7,可以获得不错的性能.本文算法中的循环增益取值明显高于基于delta函数分解的CLEAN算法中循环增益的取值,这是因为本文算法使用了拟合技术对初始参数进行了再一次优化,而基于delta函数分解的CLEAN算法中并没有进行再优化的过程.

本文算法的优点是,能够重建出高质量图像的同时提高了反卷积速度.为了比较不同加权情况下的反卷积速度,分别使用自然加权、均匀加权和鲁棒加权计算脏图.图像尺寸为256×256像素.在空间频率域使用不同的加权机制会得到不同的点扩展函数,同时得到不一样的脏图.一般来说,均匀加权得到的点扩展函数旁瓣较少,自然加权得到的点扩展函数旁瓣较高,而鲁棒加权得到的点扩展函数的旁瓣水平介于两者之间.在当前比较典型的普通计算机(Intel(R)Core(TM)i7-3770 CPU@3.4 GHz,4.00 GB RAM)上,本文算法(Python实现)处理256×256大小的图像大概在几分钟完成.正如其他算法一样,参数不一样时,迭代次数不一样,因而反卷积所用的时间也会不一样.

图1 本文算法处理M51的结果.(a)真实图像;(b)使用鲁棒加权形成的脏图;(c)重建的模型图像;(d)对应的重建图像.Fig.1The results of M51 processed by our algorithm.(a)The true image;(b)the dirty image with robust weighting function;(c)the reconstructed model image;(d)the corresponding restored image.

图2 典型CLEAN算法的结果比较.(a0)Hg-Clean算法[2]的模型图像;(a1)Hg-Clean算法的残差图像;(b0)多尺度CLEAN算法[9]的模型图像;(b1)多尺度CLEAN算法的残差图像;(c0)Asp-Clean算法[11]的模型图像;(c1)Asp-Clean算法的残差图像;(d0)本文算法的模型图像;(d1)本文算法的残差图像.Fig.2 The results compared with that of typical CLEAN algorithm.(a0)The modeled image from the Hg-Clean algorithm[2];(a1)the residual image from the Hg-Clean algorithm;(b0)the modeled image from the Ms-Clean algorithm[9];(b1)the residual image from the Ms-Clean algorithm;(c0)the modeled image from the Asp-Clean algorithm[11];(c1)the residual image from the Asp-Clean algorithm;(d0)the modeled image from our algorithm;(d1)the residual image from our algorithm.

表1中比较了不同加权机制下的性能.从表中可以发现:(1)本文算法的分量数目多一些.这是由于自适应尺度像素分解算法采用了有效集,部分分量被多次优化,有利于减少分量数目.(2)单次迭代所花时间缩短了3倍以上,同时单次迭代所花的时间也有较大的差异.这种差异部分来源于自适应尺度像素分解算法中的有效集大小的不同.当其他参数确定时,有效集的大小取决于点扩展函数的旁瓣水平.(3)整体上,本文算法速度提高了3倍左右.

表1 在不同加权机制下的性能比较Table 1 Performances with different weighting functions

在不同图像大小情况下(其他参数一致,并使用均匀加权),对比了本文算法与自适应尺度算法之间的反卷积速度.从表2可以看出,对于256×256,512×512,1024×1024,2048×2048的图像大小,本文算法的反卷积速度均有提升.另外,速度的提升并不是随图像的大小而线性增加的,这可能是由于CLEAN反卷积过程本身是一个非线性过程导致的.

表2 在不同图像大小情况下的速度比较Table 2 Runtime with different image sizes

4 总结与讨论

自适应尺度像素分解算法在射电综合成图中可以获得当前最好的重建效果,然而其计算时间却很长.本文针对这个问题,在自适应尺度像素分解算法基础上,使用不同的初始值计算方法和拟合策略.实验表明,本算法在获得高质量重建图像的同时,反卷积速度有较为明显的提升.

反卷积研究的是如何有效地找到分量来逼近真实的天空亮度分布,是射电综合成图中的关键技术.大量研究给出了不同的反卷积方法,然而这些方法往往适用于某一场景.比如,Hg-Clean算法适用于很好分开的致密源场景,而自适应尺度像素分解算法对延展源更有效.尽管自适应尺度像素分解算法解决了尺度自适应问题,提高了重建图像的质量,然而导致了时间开销显著增加[11].本文提出了一种保持与文献[11]具有同等重建质量且有速度提升的算法,应用场景与文献[11]一致.然而,针对不同的应用场景,当前并没有相对普适的算法,所以提出更有效的方法逼近各种场景的天空亮度分布仍然是下一步的研究方向.