主动型氢原子钟性能监测及评估方法研究∗

白杉杉 董绍武 赵书红 张继海

(1 中国科学院国家授时中心西安710600)

(2 中国科学院时间频率基准重点实验室西安710600)

(3 中国科学院大学北京100049)

(4 中国科学院大学天文与空间科学学院北京100049)

1 引言

时间基准通常由具有一定规模的钟组产生和保持,主动型氢原子钟作为钟组的重要部分,不仅是生成时间尺度的一份子,在守时系统中通常作为主钟,用于输出标准时间频率物理信号,直接影响时间基准的性能.氢原子钟具有短期稳定度好,相位噪声低等特性,目前在国际原子时TAI及各地方时间尺度中的作用日益重要,各家守时机构也越来越重视氢原子钟的应用.因此,研究氢原子钟性能监测方法,可以预报钟性能的变化,及时发现故障,从而减小对时间基准系统性能的影响.研究氢原子钟性能评估方法,从影响性能最主要的频率稳定度及“可预测性”两个方面定量评估氢原子钟的性能,可以为原子时尺度计算提供参考,以期将氢原子钟的优势最大程度地发挥到守时应用中.

2 基本原理

2.1 重叠式Hadamard方差

Hadamard方差是基于Hadamard变换的1种用于时域频率稳定度表征的3次取样方差.重叠Hadamard方差是按照3次取样Hadamard方差的满迭代估算,对于频率数据,它的表达式为[1]:

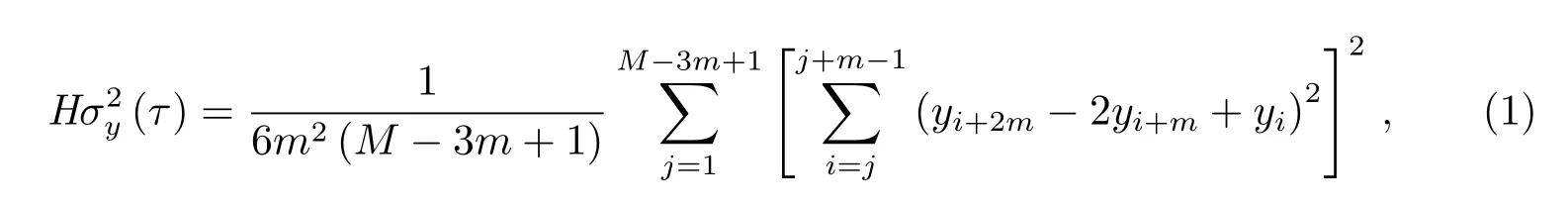
其中,为1组相对频率值y的Hadamard方差,yi为采样间隔为τ(τ=mτ0,其中,τ0为基本测量间隔)的M个相对频率值的第i个频率值.

对于相位数据,它的表达式为:

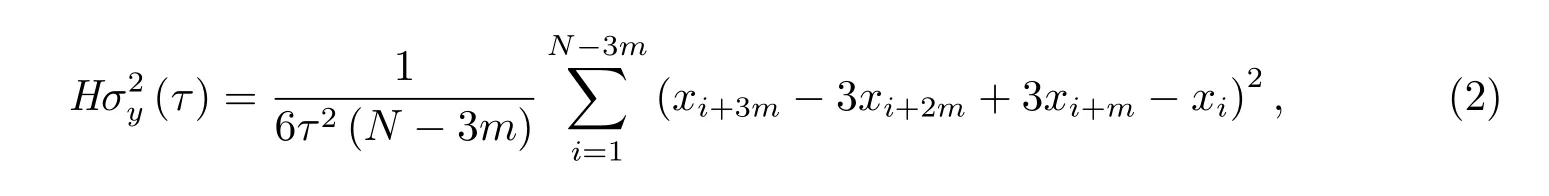
其中,xi为采样间隔为τ的N个相位差的第i个相位差,N为M+1.

2.2 多角帽法

假设、为两台钟在已知τ间隔内各自的Hadamard方差,为在同样间隔内相互比对得到的Hadamard方差,假定各钟之间相互独立,我们有[2]:

其中,E表示数学期望.对于3台钟的情况,根据(3)式有:

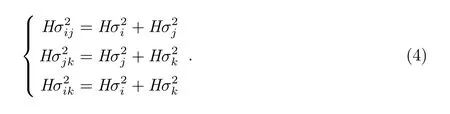
最后,我们可以得到每1个钟的方差为:

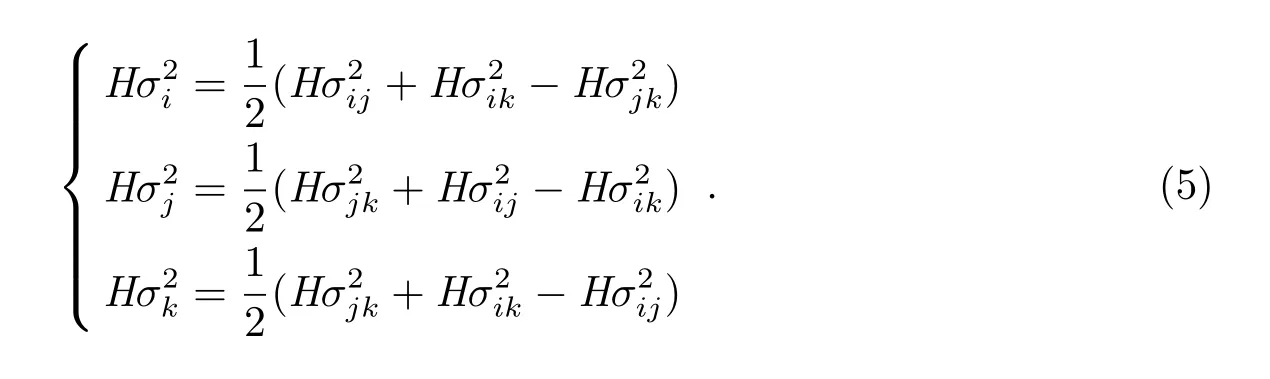
上式在时频工作中称为三角帽法,这种估计方法可以推广到Q(Q>3)台钟的情况:

3 氢原子钟性能监测方法

氢原子钟在安装并正常运行后,不需要做进一步调整,但每台原子钟都有各自的物理状态参数.该参数反映了钟内部系统的物理特征、电子器件的运行状态等,可以通过串口进行实时采集和存储,对物理状态参数进行分析和评定,以实现对氢原子钟运行状态的监测,及时发现故障并采取有效的预防措施,保证氢原子钟的可靠运转.

3.1 物理状态参数介绍

氢原子钟的状态参数采集通道共有32路,其中26路为状态参数采集值,分为7大类:接收机、腔自动谐振系统、氢源、真空泵、加热器、电源及其他,如图1所示.每1项参数值都有其正常范围及典型值,具体含义见氢原子钟手册.

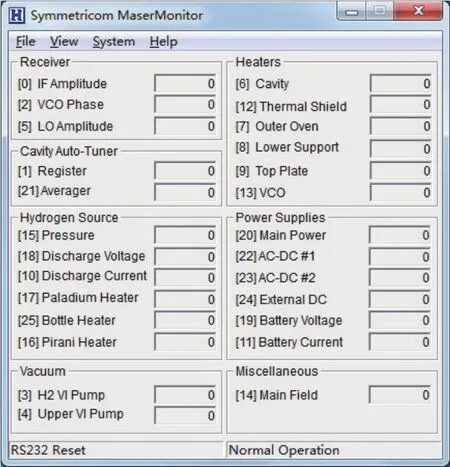
图1 氢原子钟状态参数Fig.1 The state parameters of hydrogen maser

另6路为报警项,是对前26项中比较重要的6项参数在超出正常值范围后会有报警提示,其中:

(a)通道26 “IF Alarm”是对通道0 “IF Amplitude”的警告指示,“IF Amplitude”是指接收机405751 Hz中频振幅的读数,在腔伺服系统最佳运转状态下,测试仪表读数应该在2.5–7.5 V之间,压力设置在“LOW”时典型值应在3–5 V之间,压力设置在“HIGH”时典型值应在5–7.5 V之间,当该项参数值低于2.5 V时会提示报警;

(b)通道27 “VCO Alarm”是对通道2 “VCO Phase”的警告指示,“VCO Phase”是指在接收机锁相环中,加在压控晶振上的电子频率控制电压缓冲的直接读数,正常值范围在±1 V以内,如果超出,氢原子钟前面板指示灯会报警;

(c)通道28 “Register Limit Alarm”是对通道1 “Register”的警告指示,“Register”是指用变容二极管控制谐振腔频率的腔自动协调伺服系统的输出电压,正常值范围为1−10 V,频率校准因子近似于5×10−12V−1,这是参考于氢原子钟的输出频率.当超出正常值范围后会有警告提示;

(d)通道29−31是对通道22−25的电源相关参数的警告指示,交流电源AC1、AC2以及直流电源DC中的任何1个都可以独立支撑整个氢原子钟的用电,3者互为备份,其中任何1个失效后都会有警告提示.

3.2 物理状态参数监测与分析

采用美国Symmetricom公司研发的“Maser Monitor”软件对状态参数进行监测和分析,该软件将状态参数进行分类显示,可以直观看出参数的变化以及是否正常,分类显示还可以对同类参数进行整体分析,便于发现问题以及准确地采取预防措施.

以在我国UTC(NTSC)时间基准系统中运行的MHM-2010型氢原子钟H297为例,用“Maser Monitor”软件监测该钟在2015年6月至12月的部分状态参数如图2所示.从图2可以看出,H297状态参数中第2通道“VCO Phase”的值虽然在正常值范围内,但是有明显的跳变.

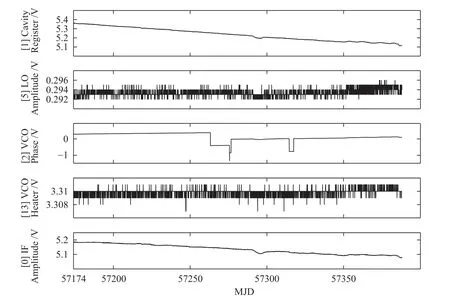
图2 H297内部状态参数Fig.2 The internal state parameters of H297

结合UTC(NTSC)与H297的比对数据分析,发现该时间段内原子钟性能明显改变,其状态参数与原子钟比对数据分析如图3所示.从图3中可以看出氢原子钟的状态参数“VCO Phase”与原子钟的频率变化之间有明显的相关性,当“VCO Phase”参数发生突变时,原子钟的频率也会发生突变.因此,对氢原子钟的状态参数进行实时监测和预警,可以及时监控氢原子钟性能的改变.

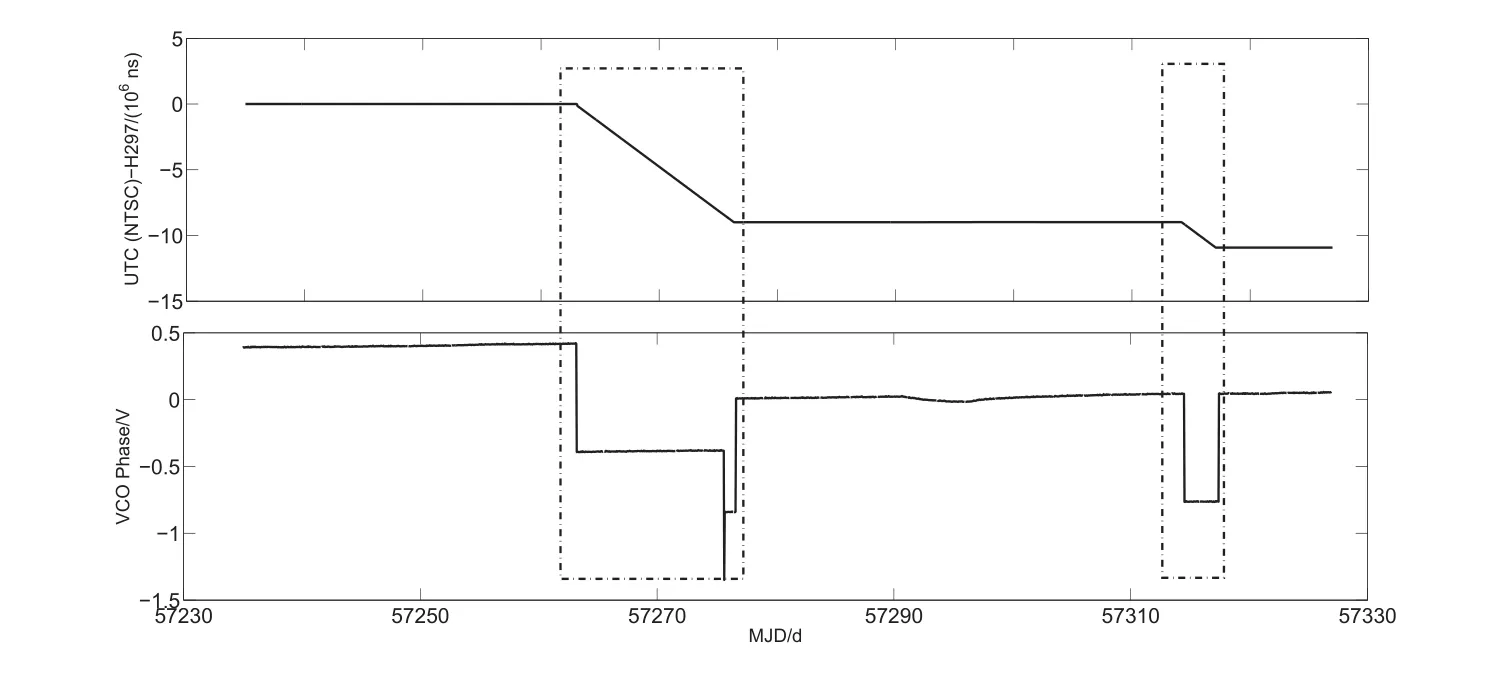
图3 “VCO phase”参数与原子钟比对数据Fig.3 The comparison of“VCO phase” parameter with atomic clock

3.3 氢原子钟性能评估方法

3.3.1 频率稳定度估计

氢原子钟的短期稳定度优于铯原子钟,在没有高一级参考标准的情况下,可以先计算出两台氢原子相互比对的频率稳定度,再利用多角帽法计算出每1台氢原子钟的稳定度[3].Hadamard方差是与双样方差相类似的3样方差,它是频率数据的2次差分,相位数据的3次差分,Hadamard方差可以扣除频率线性漂移对其的影响,而重叠式Hadamard方差比Hadamard方差有更好的置信度[4],因此重叠式Hadamard方差可以准确表征氢原子钟的频率稳定度.首先利用(2)式计算出氢原子钟两两互比的频率稳定度,再通过(6)式计算出每台氢原子钟的频率稳定度.

选取16台CH1-75型及MHM-2010型氢原子钟.计算2017-02-01—2017-11-30每台氢原子钟1–60 d的频率稳定度,如图4所示.从图4中可以看出绝大多数氢原子钟的稳定度在6 30 d的情况下是基本稳定的,在>30 d的情况下受频率漂移的变化和随机游走噪声等因素的影响表现出了差异性和不稳定性,因此,在氢原子钟频率预报中,频漂项在30 d内一般假定是不变的,超过30 d需要重新计算.从CH1-75型氢原子钟频率稳定度图中可以看出,H3840、H3841、H3852的中长期稳定度优于H3845、H3811、H3844、H3817,而H3853在>30 d的稳定度明显增大.从MHM-2010型氢原子钟频率稳定度图中可以看出,H0702、H0722、H0724、H0725、H0731的中长期稳定度优于H0735、H0720、H0715.

图4 氢原子钟频率稳定度Fig.4 The frequency stability of hydrogen maser

3.3.2 氢原子钟“可预测性”评估

当1台原子钟具有很明显的特征,例如频率漂移或是老化现象,这种特征可以很好地被预测并能够合理地被修正,那么这台原子钟就认为“好钟”.能被准确预测并修正即为钟的“可预测性”.2014年1月,BIPM(Bureau International des Poids et Measures)提出基于“可预测性”的新权重算法,该算法修正了频率漂移对氢原子钟长期稳定度的影响,提高了氢原子钟在国际原子时尺度TAI计算中的地位,因此“可预测性”是评价氢原子钟性能的重要指标.

对“可预测性”的量化方法是评估钟“可预测性”的重点.从3.3.1节稳定度分析中得出氢原子钟频漂在30 d内可以假定是不变的,超过30 d以后需要重新计算.因此,需每月对氢原子钟进行1次频率预报.由于在BIPM中对于1台新加入系统的原子钟需要累积6个月的数据才能给出该钟在TAI中所占的权重,因此,每月计算氢原子钟预报速率与真实速率之间的残差并累积6个月后,计算残差的RMS(Root Mean Square)值,以RMS值作为钟“可预测性”的定量评估,RMS值越小说明“可预测性”越好,反之则越差.RMS计算公式如下:

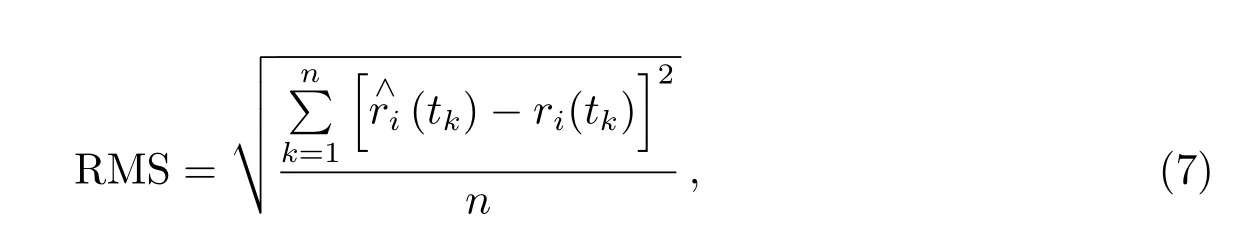
其中,(tk)表示原子钟i在tk时刻的预报速率,ri(tk)表示原子钟i在tk时刻的真实速率,n表示原子钟i的预报残差个数.

文中介绍了两种不同的氢原子钟频率预报模型,一种是基于BIPM公布数据的预报模型,另一种是基于2次多项式的预报模型.

(1)基于BIPM公布数据的预报方法

对于参与TAI计算的原子钟,可以依据BIPM公报发布的上个月原子钟的频率和频漂值,预报当月的频率值,频率预报公式为:

其中,di(tk−1)为原子钟i在tk−1时刻的实测频漂.

选择上述16台CH1-75型及MHM-2010型氢原子钟,利用2017年5至10月BIPM每月公布的原子钟频率及频漂文件,利用(8)式对2017年6至11月每月的原子钟频率进行预报,再利用(7)式计算预报残差的RMS,原子钟的“可预测性”如图5所示.从CH1-75型氢原子钟图中可以看出,H3840、H3841、H3852的“可预测性”优于H3845、H3817、H3844、H3853、H3811. 从MHM-2010型氢原子钟图中可以看出,H0702、H0724、H0725、H0731、H0722的“可预测性”优于H0735、H0720、H0715.均与3.3.1节稳定度分析结果相符.

图5 基于BIPM公布数据的原子钟“可预测性”Fig.5 The“predictability” of atomic clock based on the data published by BIPM

(2)基于2次模型的预报方法

在2次模型预报中,首先需要一个参考RTA(Reference Atomic Time),这个参考可以是比氢原子钟更高一级的频率标准,如:铯原子钟喷泉钟、锶光钟等,也可以是国际公认的标准时间,如:UTC(Coordinated Universal Time)、UTCr(Rapid UTC)等,还可以是利用多台原子钟经过时间尺度算法计算出来的时间尺度[5].选定一个合适的参考,将氢原子钟(clockHi)与参考RTA比对,得到比对数据:(RTA-clockHi),对该数据进行2次建模,利用最小二乘法估计出氢原子钟的频率、频漂,即为钟的预报频率、频漂,计算出预报残差,并利用6个月预报残差RMS评估该钟的“可预测性”.计算流程如图6所示.

氢原子钟2次预报模型公式如下[6−8]:

(a)一个稳定、可靠评价氢钟的参考

氢原子钟的中、短期稳定度较好但是长期来看存在频率漂移,对于频漂的估计是2次模型拟合的关键,因此,要求参考的长期性能好,在这里,我们选用UTC(NTSC)时间基准系统中5台氢原子钟和27台铯原子钟利用ALGOS算法,计算得到最终作为评价氢钟的参考时间尺度RTA.

选用2017-02-01—2017-11-30的原子钟Clocki比对数据(UTC(NTSC)-Clocki),计算出参考原子时尺度,并结合BIPM发布的Circular T的数据,验证RTA计算的准确性,如图7所示.从图7可以看出,RTA-UTC(NTSC)和UTC-UTC(NTSC)的数据相关性很强,这说明RTA与UTC是吻合的,因此,RTA可以作为计算氢原子钟的频率和频漂的参考.

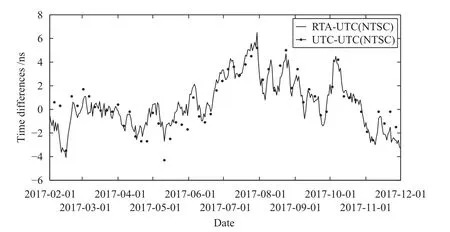
图7 RTA的结果分析Fig.7 Analysis of RTA results

(b)“可预测性”评估

选择上述16台CH1-75型及MHM-2010型氢原子钟,利用(9)式对每台钟2017年6至11月的钟速进行预报,并利用(7)式计算预报残差的RMS,原子钟的“可预测性”如图8所示.从CH1-75型氢原子钟图中可以看出,H3811、H3817、H3844、H3840、H3841、H3852的“可预测性”优于H3845、H3853. 从MHM-2010型氢原子钟图中可以看出,H0702、H0724、H0725、H0731、H0722的“可预测性”优于H0735、H0720、H0715. 与基于BIPM公布数据的预报结果基本相符.

图8 基于2次模型的原子钟“可预测性”Fig.8 The atomic clock’s “predictability” based on the quadratic model

(3)“可预测性”验证

2014年起,BIPM开始采用钟的“可预测性”计算原子钟在TAI所占权重,因此,用BIPM公布的权重文件对上述氢原子的“可预测性”进行验证,选择2017年11月的权重文件,上述原子钟在TAI中所占权重如图9所示,因为BIPM要考虑时间尺度的可靠性,所以设置了最大权限制[9].对比图9和图5、图8可以看出,基于BIPM数据预报的原子钟“可预测性”在0.175以下的原子钟均取得了0.962的权重(满权),基于2次模型方法预报的原子钟“可预测性”在0.055以下的原子钟均取得了满权.

计算图9中没有取得满权的3台MHM-2010型氢原子钟在TAI中所占权重与钟的“可预测性”相关系数如表1所示.从表1可以看出,未取得满权的3台原子钟在TAI中所占权重与钟的“可预测性”是负相关的.

表1 钟的权重与“可预测性”相关系数Table 1 The correlation coefficient between weight and “predictability” of clocks

从图9和表1的分析结果说明,不管是基于BIPM公布数据的预报方法还是基于2次模型的预报方法计算出来的钟“可预测性”均与BIPM计算出来的权重结果吻合,因此,两种预报方法均可以有效地定量评估钟的“可预测性”.

图9 氢原子钟在TAI中所占权重分布图Fig.9 The weight of hydrogen maser in TAI

4 结论

在氢原子钟性能监测中,原子钟状态参数与比对数据联合分析结果表明,状态参数监测可以预报钟性能的变化,从而为原子钟性能评估及原子时计算提供参考.

在氢原子钟性能评估中,原子钟频率稳定度与“可预测性”结果吻合,中、长期稳定度越高的原子钟“可预测性”也越好.文中给出了两种原子钟频率预报方法,基于BIPM公布数据以及基于2次模型方法计算出来的预报残差RMS值虽然略有不同,但对于原子钟“可预测性”的评估结果基本一致,两种预报方法各有优缺点.基于BIPM公布数据的预报方法简单易操作,但实时性差,需要依赖于BIPM公报,一般滞后45 d左右,而且对于没有直接国际溯源比对链路的实验室,从BIPM公报上无法得到对应原子钟的频率及频漂文件,就只能利用基于2次模型的预报方法,该方法实时性好且适用广泛.BIPM权重验证结果表明,两种预报方法计算出来的钟“可预测性”均与BIPM公布的权重比例相吻合,可以作为钟“可预测性”的定量评估方法.