一种基于差分的长波授时方法研究∗

燕保荣 李 云 郭 伟 华 宇

(1 中国科学院国家授时中心西安710600)

(2 中国科学院精密导航定位与定时技术重点实验室西安710600)

1 引言

长波授时是一种利用长波信号进行标准时间发播和传递的方法,长波信号具有覆盖范围广、传播稳定、抗干扰性能好的特点[1−2],能够绕过高山、建筑物等继续传播,更适合在陆地上授时.通常,长波授时利用天波与地波相结合的方式传播标准时间信号.其中地波授时是通过沿地球表面传播的电波信号进行授时服务的方式[3].众所周知,卫星授时是目前使用最为普遍、授时精度相对较高的授时手段,也是目前主要的授时方式.但是,卫星授时也有其自身的弱点[4],存在安全隐患.首先,卫星导航授时系统在非常时期可能无法保障授时服务;其次,卫星信号易受干扰和欺骗;同时,在高楼林立的大城市和森林密集地区,信号易遮挡,这些弱点都会给国民经济,甚至是国家安全造成极大的危害.与卫星授时相比,长波授时的精度不高.但是,它对电离层、太阳风暴等自然扰动不敏感,即使核爆也不会受严重干扰,人为干扰更是困难,使得它在未来战争的极端恶劣环境条件下成为提供大面积应急指挥控制通信的一种重要手段[5].并且,长波系统能满足航空非精密进近和港口进近对位置信息和时间频率的需求,是卫星导航系统最可行、最可靠的备份[4].

近年来,卫星授时的弱点日益突出,高质量的长波授时又成为国内外学者研究的热点[6−11],尤其是如何提高长波授时的精度.在长波授时的影响因素中,由于受地面电导率的影响,附加二次因子(Additional Secondary Factors,ASF)难以模型化处理并精确计算[6].目前,对ASF数据的处理方法主要是:在某个地区进行大量测试,并对测试数据进行相应的处理,然后再加载到用户接收机中供用户使用.这种方法的缺点是:测试数据只能代表某特定时间的变化情况,实时性差.同样,利用GPS/eLoran(enhanced Loran)的组合定位系统可以分析特定位置ASF的变化情况,数据处理方法基于采集数据的时长,因此其计算结果也受时长及采集时间的影响[7].同时,ASF的测量精度受多种误差的影响.根据误差传播定律,主要的误差源包括到达时间(Time of Arrival,TOA)的测量误差、标准时标误差、数据处理误差、发射机抖动误差等.将ASF的修正值用于长波的高精度授时,需要在用户接收机中内置精确的ASF数据库,该数据库的建立需要大量数据的测量及误差消除处理,且受处理方法的影响.本文将差分原理应用于长波授时,提出了一种差分时延改正数近实时的计算方法,并将其应用于用户时延的修正,可有效提高长波的授时精度.

2 长波授时

2.1 长波授时原理

长波授时系统的发播设备不间断地向外发送与导航定位和时间频率相关的信息.用户利用长波定时型接收机接收到相关信息后,首先经过解码获得其所在实际位置的时码信息,再精确测量出定时接收机本地秒信号与接收到的秒信号之间的时延差,用于校正本地秒,从而完成定时.图1给出了用户利用长波进行定时时的基本时间关系,其中,Tm为长波授时台的标志脉冲1PPS与标准时间UTC的1PPS的时间偏差;Tp表示授时信号从主台发射天线到用户接收机天线的传输时间;Tr表示授时信号在用户接收系统内的时间延迟,包括接收天线、耦合器、电缆和接收机通道对接收信号的总延迟;∆T为接收机的本地1PPS与UTC的1PPS之间的时间偏差;N为接收机本地秒信号与接收机组触发脉冲(Group Trip Pulse,GTP)之间的时间间隔,在统一的时间轴上满足[3]:

在图1中,Tm值的大小取决于长波授时系统对定时信号发射时的控制精度,可以通过电流回路进行精确测量,在理论上是已知值.对于本身地理位置已知的用户,Tp可以通过相应的计算公式预先估计,也就是说在定时接收机内部需要配置时延预测的计算程序.Tr可以通过标校获得,定时接收机如果能够测出N,用户就可以根据(1)式确定接收机本地钟和基准时钟之间的钟差∆T.用户接收机利用上述的计算量进而自动控制接收机本地输出的1PPS同步到标准时间UTC的1PPS上,完成定时.可见,利用长波信号进行定时或同步,要求准确预测电波传播的绝对时间延迟量,即传播时延值Tp.在不考虑发播控制精度和接收端接收系统时间延迟精度的前提下,定时的精度完全取决于传播时延Tp的计算精度,也就是说,传播时延Tp计算越准确,用户的定时精度就会越高.因此,传播时延Tp的精确预测是长波定时中最为关键的问题[12].

图1 基本的时间关系Fig.1 Timing principle

2.2 长波传播时延及影响因素

传播时延是信号由发射天线发出并沿地面传播,在到达接收天线之前所经历的时间延迟量,长波传播时延Tp的预测是长波授时的关键,其时延预测的精度直接决定了长波授时的精度.通常,长波传播时延可以表示为:

(2)式中,tp为基本时延,是指信号从发射台到接收点在大气中传播所对应的时间延迟,ts为二次时延,是指信号从发射台到接收点在实际路径中传播相对于空气中传播所增加的时间延迟[13].

当长波授时信号在理想的真空中传播时,其长波传播路径上的时延就是基本时延,表示为:

(3)式中,R表示传播路径的距离,n0是真空中的折射率,取值为1,c为真空中的传播速度.可见,tp由传播路径的距离以及信号传播的速度决定.当长波信号是在真实的大气中传播时,大气的折射率会对传播的授时信号产生影响,而大气折射率又是随时间和空间变化的量,会引起授时信号传播速度和方向的变化,从而影响传播时延.将长波授时信号的基本时延表示为空间位置和时间变化的函数,其计算公式为:

(4)式中,ns(s,t)是大气的折射率,是传播距离和时间的函数.ds是传播距离的微分量.由于ns(s,t)的空间分布很复杂,并且随时间变化,其积分很难计算.考虑到大气折射率的缓变特性,通常按照我国电磁波行业的标准,将ns(s,t)的平均值取为:ns0=1.000315.传播路径的距离需要按照传播的实际路径计算,考虑到传播路径上高山、河流、森林、城市等因素引起的路径计算复杂性,可以根据收发两点的精确坐标按照标准椭球的大地线距离进行计算,用Rd表示.这样,基准时延tp就可以分为能定量计算的部分和不能定量计算的部分,表示为:

其中,Rdns0/c表示基准时延的确定量,∆tp为基准时延的不确定量,包含了大气折射率的部分影响以及传播路径距离误差的影响等.

二次时延ts反映了真实传播路径与大气传播中时间延迟的差异,由传播路径上衰减函数的相位表示:

(6)式中,w=2πf,是信号的圆频率,单位为rad/s,f为信号频率,单位为Hz.argW是地波衰减函数W的相位,单位为rad.通常W与传播频率f、传播距离R、传播路径上的相对介电常数ε(s)、电导率σ(s)等参数有关,表示为W=W(f,R,ε(s),σ(s)).信号的传播频率是确定的,可以取传播路径距离与基准时延中的传播距离相同,传播路径上的相对介电常数ε(s)和电导率σ(s)也是难以精确确定的,甚至受实时性因素的影响,将其用等效的相对介电常数εe和等效的电导率σe表示.当εe和σe为已知量时,采用和基准时延相同的处理方法,ts同样可以表示为:

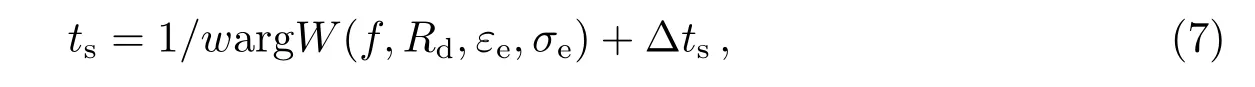
其中,1/wargW(f,Rd,εe,σe)表示二次时延中的确定量,∆ts为二次时延中的不确定量,包含了传播路径距离误差的影响、等效介电常数和等效电导率等误差的影响.

可见,长波授时信号传播路径上的传播时延Tp能具体表示为:

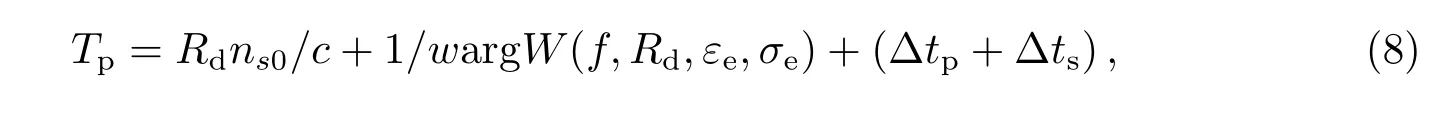
其中,(8)式中前两项的和是可以利用相关公式进行计算预测的.∆tp+∆ts是传播路径时延计算中的不确定项,也是影响长波授时精度的关键因素.和前两项的和相比,该值是一个小量,在定时精度不高的情况下,可以忽略.对于高精度的授时,就需要考虑这些不确定因素的影响.

2.3 长波传播时延的间接测量

从2.2节的描述可知,在进行高精度授时时,根据相关公式直接预测Tp难以满足高精度定时的需求.考虑到卫星授时精度高、使用普遍的特点,用户可以借助于GPS授时、共视等辅助手段通过间接测量获得长波传播路径上的时延值[8,14].图2给出了长波传播时延Tp间接测量的关系示意图,直接的观测量表示为N.根据相应关系可得:

其中,∆t表示发播台的标准1PPS与参考标准GPS的1PPS的时间偏差,可以利用时间间隔计数器直接测量获得.Tr为接收系统时延,可以通过标校作为已知量.间接测量长波传播时延Tp的实质是将发播台的标准时间在用户接收点上进行复现,从而测量传播路径上的时间延迟.这样的用户接收点在功能上相当于一个监测基准站.理论上,(8)式与(9)式的结果是等价的.需要注意,在长波传播路径时延的间接测量中,测量结果N中既包含了传播路径时延,接收机处理时延等,也包括大气的噪声、发射机的抖动、接收机的噪声、射频干扰等,这些噪声体现为随机噪声,并且难以消除.故而利用(9)式获得的传播路径时延也包含了相应的随机噪声的影响.

图2 长波传播时延的间接测量Fig.2 Indirect measurement of long-wave propagation delay

3 长波差分授时

3.1 长波传播时延的空间相关性

长波发播台的信号向四面八方辐射,在接收点上利用定时接收机完成本地时间与标准时间的同步.如果两接收点的位置相近,信号从发播台到两个接收点所经历的传播路径相似,传播路径上的相对介电常数和电导率也近似相同,即两点存在一定的空间相关性.图3给出了两接收点的空间示意图以及相应的测试方法.假设发播台位于A点,两用户接收机分别位于B、C两点,将两接收点同时作为监测的基准点,采用间接测量的方法获得Tp1和Tp2,用以分析两接收点上的空间相关性.

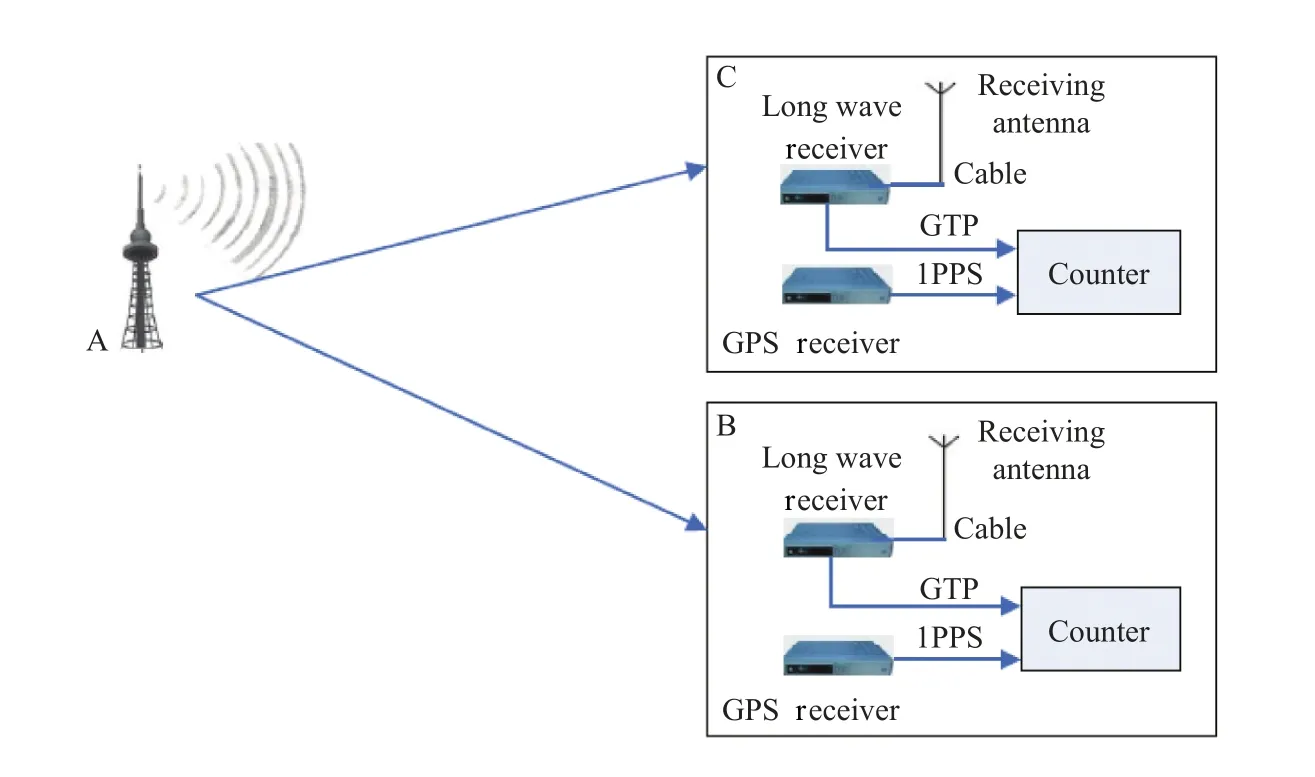
图3 不同接收点空间相关性示意图Fig.3 Diagram of spatial correlation at different receiving points

图4给出了B、C两点上获得的相同时间段内GPS的1PPS与长波接收机GTP信号之间的时延差N1和N2(图4中的实线部分),从图中可以看出,B、C两点的间接测量值随着时间的变化具有相同的变化趋势,即两者之间具有极大的相关性,可以利用相关系数表示.为了分析Tp1和Tp2之间的空间相关性,可以根据(9)式计算出Tp1和Tp2,也可以借助于N1和N2进行定量计算.因为发播台的标准1PPS与参考标准GPS的1PPS的时间偏差以及长波接收机的接收系统时延是固定值,对相关系数的计算无实质影响.由于测量值中的随机噪声无相关性,故需要对B、C两点的测量值N1和N2进行拟合,消除随机噪声后再计算相关系数.相关系数是任意变量线性相关性的测量标准,其计算公式为[9]:

其中,K为采样序列中的数据个数,和σN1分别为测量序列N1的平均值和标准偏差,和σN2分别为测量序列N2的平均值和标准偏差.图4也给出了B、C两点测量值6阶多项式的拟合结果(图4中的虚线部分),由此计算的相关系数为0.9488,表明B、C两点的测量值高度线性相关.

图4 不同接收点传播时延的测量值Fig.4 The measurement of propagation delay at different points

在计算相关系数的过程中,首先需要对测量数据进行多项式拟合,以消除随机噪声对相关系数的影响.多项式拟合的阶数不同,对随机噪声的抑制程度不同,用拟合残差的标准偏差对其拟合结果进行综合评估,表1给出了测试值N1与N2的1–10阶多项式拟合时对应残差的统计结果以及相关系数.从表1中可以看出,拟合残差的平均值都非常小,近似为零.标准偏差STD随着拟合阶数的增加而减小,说明多项式拟合的阶数越高,拟合结果越接近真实测量值.但是其相关系数与拟合阶数有关,当拟合阶数为1阶时,相关系数为1,说明两序列完全线性相关.随着拟合阶数的增加,相关系数减少,表明随机噪声开始影响相关系数.虽然拟合阶数对相关系数有影响,当阶数小于10时,相关系数都大于0.90,这种变化趋势显示B、C两点的测量值显著相关.

3.2 长波差分授时

长波差分授时就是利用监测基准站与用户站之间的空间及时间相关性,将传播路径上的不确定影响因素打包到差分改正数中,生成差分时延改正数,用以提高一定范围内其他长波授时接收机(用户点)的授时精度.长波差分授时的关键是利用间接测量的传播时延计算长波传播路径上的差分时延改正数,并以此修正用户接收机传播路径上的时延预测值,实现对用户本地时间的高精度校准.利用差分进行高精度授时时,要求用户站与监测基准站在空间上存在相关性.从差分的基本原理可知,用户站距离基准站越近,其相关性越强,授时精度也越好.相反,用户站距离基准站越远,其相关性减弱,差分效果也会相应减弱.用户修正算法是差分改正数计算的逆过程.需要说明的是:差分改正数的计算是基于基准站的实时观测值,但是用户站的修正算法只能利用差分基准站建立的改正预报模型,因此,其预报模型也是影响其精度的重要因素.这种授时方法的优点是无需考虑发射台到监测基准站和用户站路径上的公共误差项,特别是传播时延中不确定因素的影响.

表1 传播时延的相关系数Table 1 Correlation coefficient of propagation delay

3.3 计算方法

在分析利用差分的长波授时方法时,必然用到相距距离不远的监测基准站和用户站.下面的讨论中,分别用Tp1和Tp2表示长波发播台到监测基准站和用户站的精确传播路径时延(无相关误差),见(11)式.

(11)式中Rd1表示长波发播台到监测基准站的大地线距离,Rd2表示长波发播台到用户站的大地线距离,ns0、εe、σe的含义同前,∆tp1、∆ts1分别表示发播台到监测基准站的基准时延、二次时延不确定量,∆tp2、∆ts2分别表示发播台到用户站的基准时延、二次时延不确定量.

差分改正数是长波差分授时中的关键一环,由于监测基准站的直接测量值包含了发播台的标准1PPS与监测基准站参考标准GPS的1PPS的时间偏差∆t1以及对应的接收系统时延Tr1,利用间接测量方法获得的监测基准站上的传播路径时延由(9)式可以得到:其中,各项的物理含义同前所述.∆t1只与监测基准站的GPS接收机有关,Tr1只与相应的接收系统有关,理论上是恒定值.将(12)式中与路径无关的项∆t1、Tr1扣除后,可以用于差分改正数的计算.下面分两种情况进行差分改正数的计算与讨论:

(1)当基准站坐标和用户站的坐标已知时,可以根据大地线距离计算传播路径上的基准时延值,结合(11)式与(12)式,基准站上的差分改正数可以表示为:

差分前用户站上预测的传播时延值可以表示为:

差分后用户站上预测的传播时延值可以表示为:

(2)当基准站坐标和用户站的坐标已知,并且传播路径上的相对介电常数εe、等效电导率σe也已知时,基准站上的差分改正数可以表示为:

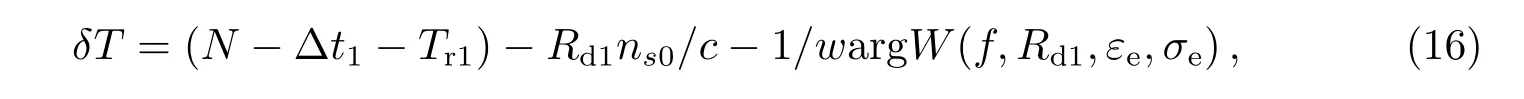
差分前用户站上预测的时延值可以表示为:

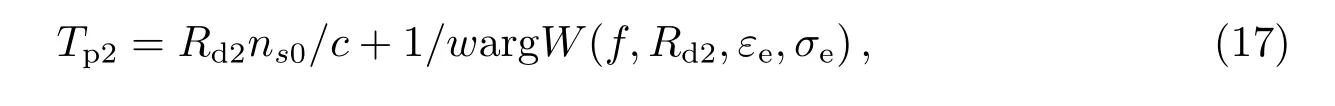
差分后用户站上预测的时延值可以表示为:

这两种差分改正数计算方法所对应的已知条件不同,用户可以根据实际情况进行选择.从差分改正数的计算过程可以看出,差分改正数包含了传播路径误差引起的时间延迟,也包含了土壤特性引起的延迟,并且体现了温湿度随时间变化的影响.用户站利用差分改正数对传播时延进行修正时,可以修正用户站传播路径上的相应误差.需要注意的问题是:在监测基准站计算差分改正数时,考虑了间接测量值中扣除参考时间的偏差∆t1以及对应接收机的接收系统时延Tr1.这就要求用户站所对应的参考时间的偏差∆t2和接收系统的时延Tr2也是已知量.如果监测基准站的∆t1、Tr1未知,也可以将其作为恒定值包含在差分改正数的计算过程中,但是需要测量基准站参考GPS接收机与用户站参考GPS接收机输出的参考信号的一致性,以及基准站长波接收机与用户站长波接收机之间的一致性,即要求两点的参考脉冲和接收系统时延一致.由于差分改正数是通过间接测量的传播路径时延获得的,该改正数中包含了传播路径距离误差的影响,也包含了相对介电常数及等效电导率计算误差的影响以及传播路径上气象条件变化的实时性影响.

4 试验验证

长波差分授时方法的有效性可以通过差分授时前后预测的传播路径时延与间接测量方法获得的传播路径时延进行比较,间接测量结果是参考.采用两台长波授时型接收机进行外场试验.两台授时型接收机同时进行静态测试,其测试方法相同,见图3,但是其目的不同.监测基准站的测试数据用于差分改正数的计算和预报,而用户站的测试数据用于差分授时效果的评估.基准测试点的坐标为(34.3685◦N,109.2222◦E),用户测试点的坐标为(34.1406◦N,108.9951◦E).两测试点距离发播台的大地线距离分别为71.163 km和103.227 km,并且基准站距离发播台较近.由于两条传播路径上的地势都较为平坦,土壤特性也近似,意味着相应的电参数近似.同时测试时,传播路径上的气象特性也相似,并且随时间变化.用户站距离基准站的距离约为32.812 km,两点的相关性较强.两点的直接测量结果见图4,其中两测试点的参考接收机进行了一致性测试,并且∆t1、∆t2的值为几十纳秒,计算过程中可以忽略.监测基准站和用户站的长波接收机利用长波信号模拟源测试其接收机信道时延[15−16],测量值分别为98.85µs、99.17µs.同时,在同一接收点上测试两长波接收机的一致性,测试结果相差0.6µs.利用传统的时延计算方法计算的发播台到监测基准站的基准传播时延值约为237.4495µs,二次时延值为1.8105µs.同样,发播台到用户站的基准传播时延值约为344.4376µs,二次时延值为2.1808µs.这里,传播介质相对介电常数取为15,等效电导率取1×10−3,地球等效半径系数为1.06.将这些测量以及计算数据用于差分改正数的计算以及授时的效果评估.

4.1 差分改正数的计算及预报

由于差分改正数的非实时性,需要将差分改正数进行预报.在利用(13)式或(16)式计算差分改正数时,虽然计算的方法不同,但是两者之间只相差一个常数,相应预报的改正数结果也只差一个常数.这里以(13)式的计算结果为例,分析差分改正数的预报效果.差分改正数的计算结果见图5.

为充分利用相关的数据,采用滑动窗形式的多项式对计算结果进行拟合及预报.这里需要考虑3个取值的影响,分别为滑动窗中拟合数据的个数,多项式拟合的阶数以及预报数据的长度.图5给出了相同拟合阶数及预报长度下,拟合数据长度对预报改正数的影响.选择的拟合阶数为1阶,预报的时长为60 s,拟合数据的个数为60、120、360,预报残差的标准偏差分别为:24.1 ns、17.1 ns、15.3 ns.可以看出,拟合数据越多,预报残差的标准差越小,意味着预报值更精确.表2给出了拟合数据长度、拟合阶数以及预报长度不同时预报残差的统计结果.从表2可以看出,当滑动窗数据长度以及拟合阶数恒定时,残差的标准偏差随着预报数据个数的增加而增大.当拟合阶数增加时,预报残差的标准偏差也有所增加,表明预报数据的误差增大.当恒定拟合阶数后,滑动窗数据长度增加时,预报残差的标准偏差减少,表明预报精度提高.参与拟合的数据个数只影响差分改正数首次计算所需要的时间,拟合的阶数则与改正数传播过程中所需要的数据位数有关.预报时长及其精度限制了改正数的发播速率和修正精度.综合考虑,用户可以选择360 s的数据进行滑动窗拟合,拟合阶数为1阶,预报6 min,这样可以减少差分改正数在传输时所占用的数据位数,并降低其更新速率.

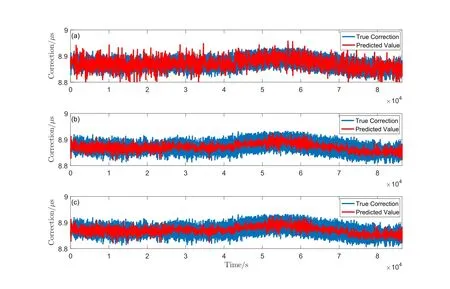
图5 拟合数据长度对预报改正数的影响.(a)拟合数据:1 min;拟合阶数:1阶;预报时长60 s;(b)拟合数据:2 min;拟合阶数:1阶;预报时长:60 s;(c)拟合数据:6 min;拟合阶数:1阶;预报时长60 s.Fig.5 In fluence of fitting data length on forecast correction.(a) fitting data:1 minute;Fitting Order:1 step;Forecast time:60 s;(b) fitting data:2 minutes;Fitting Order:1 step;Forecast time:60 s;(c)fitting data:6 minutes;Fitting Order:1 step;Forecast time:60 s.

4.2 差分效果

长波传播路径时延的预测精度会直接影响长波授时的精度,在不考虑发播控制误差、接收系统时延误差的情况下,Tp的预测精度可以直接反映授时的精度.因此,长波授时差分前后的授时精度都可以用Tp的预测误差(真实值-预测值)来表示.预测误差越小,代表Tp的预报精度越高.为了分析这种差分计算方法对授时的影响,对外场监测基准站和用户站两测试点的采集数据按照3.3节中提到的两种差分修正方法进行处理与计算,图6给出了用户站上实测的传播时延值以及两种修正方法计算的结果.从图中可以看出,实测值与预测值具有相似的变化趋势,并且方法(1)与方法(2)的结果只相差一个常数.该常数与计算过程中两测试点的长波接收机通道时延差和两测试点上的二次时延差有关.

以用户站上间接观测的传播路径时延值为参考,图7给出了测量参考值与传统时延预测结果误差以及测量参考值与两种修正方法的时延误差.左图为方法(1)的结果,右图为方法(2)的结果.从图中可以看出,差分后的时延误差都比差分前小,说明两种修正方法有效.比较左右两图结果可知,右图中差分前后的结果都优于左图中的结果,这是因为后者没有考虑二次时延的影响.需要注意,左图中差分前的时延误差近10µs,这是差分前的时延预测计算过程中未考虑接收天线延迟、距离误差延迟等因素的影响,而差分后的结果利用了接收机的测量数据,包含了相应的误差.同理,本文中差分授时方法(2)的结果优于方法(1),也没有考虑相关介电常数和等效电导率在取值方面的影响.如果要评估两种计算方法的优劣,就需要扣除相关误差的影响.

表2 拟合残差数据统计Table 2 The statistics of the fitting residual difference

图6 传播时延的实测值以及预测值Fig.6 Measurement value and predicted value of propagation delay

图7 差分前后真实值与预测值的差.左图:方法(1);右图:方法(2)Fig.7 The difference between the true value and the predicted value.Left:method(1);Right:method(2)

5 结论

本文在长波授时基本理论的基础上,分析了影响长波授时精度的主要因素,特别是传统长波授时精度难以提高的主要原因.结合长波传播信号的稳定性特点,并利用长波传播路径时延的间接测量,通过相关系数分析了相距不远的两用户点上传播路径时延的空间相关性,以此研究了长波差分高精度授时的新方法.本文提出了一种基于差分的长波传播时延预测计算方法,并应用于授时.在两种典型情况下给出了差分改正数的计算方法以及对应的用户修正算法.差分改正数中包含了传播距离误差、气象因素以及传播电参数等因素的实时影响,也包含了接收机等随机噪声的影响.扣除发播控制误差以及接收系统时延的影响,差分改正数可以体现传播路径时延的实时变化.当差分基准站与用户站之间存在较强的相关性时,这种差分计算方法具有普适性,能够有效修正用户传播路径上的时延误差.但是差分效果需要根据差分基准站以及用户站所在位置、传播距离等具体情况进行分析.在差分授时过程中,差分改正数的计算及预报是其中的重要环节,本文讨论了影响改正数预报精度的因素,包括拟合数据长度、拟合阶数以及预报时长等.利用多项式拟合的方法分析了影响差分改正数预报结果的因素.结果表明:在拟合数据和拟合阶数一定时,预报时间越长,预报效果越差.结合测量数据对差分前后的授时精度进行了评估,计算结果表明:基于差分的授时方法可以有效提高授时精度.在本文的讨论过程中,差分改正数计算时未考虑接收机天线的影响,尽管该值可以作为常数包含在改正数中,但是却影响了差分授时的改正效果.同理,相关介电常数和等效电导率也会对授时方法的探讨产生影响.在以后的工作中,希望可以解决相应的问题,进一步提高差分授时的精度.