基于姿态角估计的四旋翼飞行器多传感器故障诊断方法

王日俊，曾志强，段能全，党长营，杜文华，王俊元

（中北大学 机械工程学院，太原 030051）

四旋翼飞行器是一种结构简单的无人飞行器，具有灵活起降、自主飞行以及稳定好等特点，在军事与民用领域存在巨大的应用潜力，因而受到各国研究人员的广泛关注和重视[1-2]。由多种传感器组成的惯性测量单元（Inertial Measurement Units, IMU）是其执行飞行任务的重要环节，对于飞行器的姿态运动控制和自主飞行控制起着关键作用[3]。但是，恶劣的机载环境存在着温度变化、机械振动等因素极易导致IMU传感器发生故障[4-5]。传感器故障的一旦发生，不仅会对飞行的安全性、稳定性造成严重影响，更会导致任务执行失败，甚至是造成地面人员的伤亡。因此，开展四旋翼飞行器传感器故障诊断技术的研究对于提高飞行器的安全性和可靠性具有重要的意义与价值。

目前，针对四旋翼飞行器故障诊断技术的研究主要集中于执行器故障，而应用于传感器故障诊断的研究成果仍然有限[6]。基于全局观测器的传感器故障诊断方法提出不久，多种观测器或估计器方法，如基于线性参数变化自适应观测器[7]、集员估计器[8]，非线性状态观测器[9]和降阶非线性观测器[10]等已被相关研究人员逐渐应用于四旋翼飞行器的传感器故障诊断方法的研究工作中。此外，基于扩展卡尔曼滤波（Extended Kalman filter, EKF）以及强跟踪卡尔曼滤波（Strong Tracking Kalman filter, STKF）的四旋翼飞行器状态与传感器故障偏差估计方法也取得了一定的研究成果[11-12]。然而，由于需引入额外的系统状态变量来描述传感器的故障，使其难以满足有限传感器测量的可观测条件，难以对参数估计的稳定性进行分析。在包括上述的研究工作在内的四旋翼飞行器的故障诊断方法均是在不考虑系统模型误差，且假设姿态角可直接测量得到的前提下进行的。然而，在实际的应用中，系统模型中的升力、转动力矩等无法测量得到，滚转角和俯仰角通常也是通过机载IMU信息估计得到的。

针对上述问题，本文在考虑四旋翼飞行器动力学模型误差的基础上，提出一种四旋翼飞行器的传感器多故障诊断及故障偏差值估计方法。该方法仅利用加速度信息对姿态角进行估计，通过基于估计姿态角的故障观测器对多传感器故障进行检测并隔离，构建非线性自适应故障偏差观测器，同时对多个故障偏差值进行估计，从而为飞行器的安全、可靠飞行提供有力的保障。

1 系统描述

1.1 四旋翼飞行器建模

图1为四旋翼飞行器的结构示意图。取四旋翼飞行器的质心O作为机体坐标系OxByBzB的原点。惯性坐标系OxEyEzE的原点与飞行器起飞位置时OxByBzB的原点重合。4个执行器Mi（i=1, 2, 3, 4）均由直流电机和旋翼组成，其中，执行器 M2、M4按顺时针方向旋转，执行器M1、M3按逆时针方向旋转。升力Fi（i=1,2, 3, 4）由4个执行器提供。飞行器通过调整4个执行器之间的转速差来完成在各个方向上的姿态转动控制。

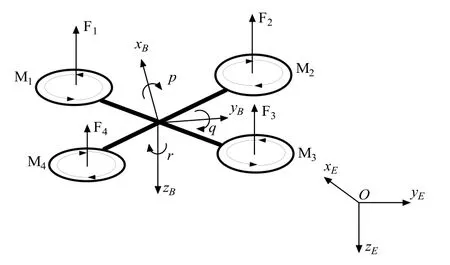
图1 四旋翼飞行器的结构Fig.1 Structure of quad-rotor aircraft

在四旋翼飞行器的实际应用中，包括旋翼电机提供的升力U，作用于飞行器绕x、y、z轴的转动力矩Tφ、Tθ、Tφ等在内的系统输入变量均无法精确测量得到，通常认为它们与电机速度的平方成正比。而电机转速则通过PWM指令以及驱动电压值估计得到。这在很大程度上造成了建模的不确定性。考虑上述因素，结合牛顿-欧拉运动学方程得到四旋翼飞行器动力学模型如式(1)所示。

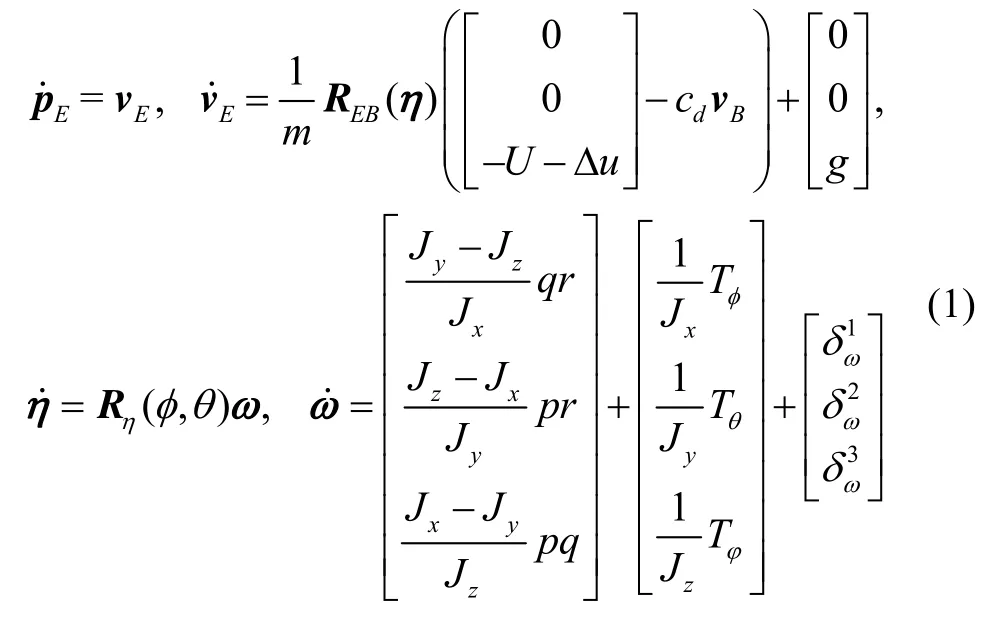
其中，m表示四旋翼飞行器的质量，g表示重力加速度，pE、vE分别表示惯性坐标系下的位置和速度，欧拉角角速度Jz分别表示飞行器绕 x、y、z轴的转动惯量；U表示由4个执行器提供的总升力；dBcv表示作用于机体的阻力，dc为阻力系数，Bv为机体坐标系下沿x、y、z方向上的速度，且为机体坐标系到惯性坐标系的转化矩阵。

假设非线性科氏力忽略不计，则四旋翼飞行器在机体坐标系下的速度可表示为[13]：

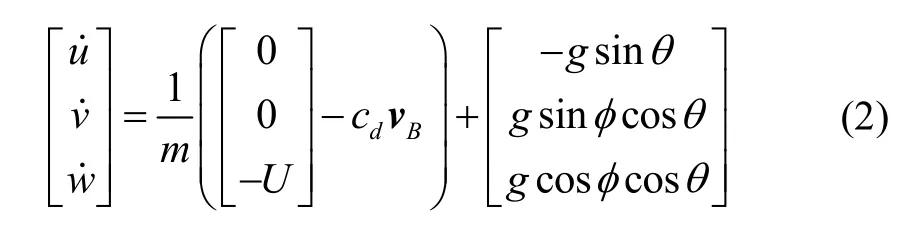
其中，φ和 ub分别表示PWM信号和驱动电压值。

1.2 传感器偏差故障建模

由于飞行器重量与体积的限制，质量轻、体积小的MEMS传感器已成为机载IMU惯性测量器件的首选，如三轴陀螺仪、三轴加速度计、磁力计等。它们在飞控系统的导航信息获取和姿态运动控制中起着关键性作用。偏差故障是一类常见且不易检测到的IMU传感器软故障，一旦发生会导致飞控系统无法正常发挥作用。在实际偏差故障发生时，加速度计与陀螺仪传感器的模型可描述为：

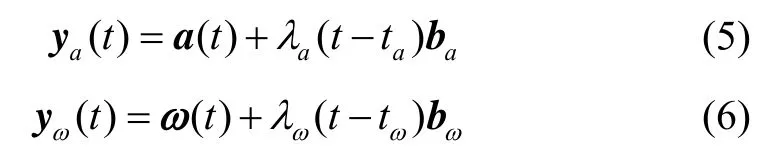
其中，ya(t)表示加速度计的实测值，yω(t)表示陀螺仪的实测值； ba表示加速度计的故障偏差值，且表示陀螺仪的故障偏差值，且表示无偏差故障时陀螺仪的测量值，且表示无偏差故障与测量噪声时加速度计测量值，且：

在实际情况下，通常故障偏差值ab、ωb随时间的变化较为缓慢，在短持续时间内ab、ωb的变化量也很小[14]。因此，可认为故障偏差值在短持续时间内是恒定的，则可做如下假设。

假设1：加速度计和陀螺仪的故障偏差值ab和ωb均为有界的常数，即：

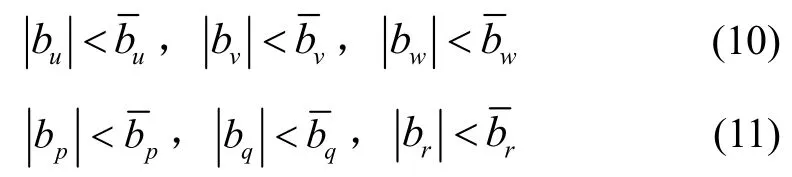
此外，系统的输出可表示为：

其中，()tψ为惯性坐标系下的飞行器的偏航角，它与飞行器的位置均可由GPS单元和磁力计测量计算得到。

2 偏差故障检测与诊断（Bias Fault Detection and Diagnosis，BFDD）系统设计

为了实现对多个同时发生的传感器故障进行检测与隔离，并通过第1节中式(1)(5)(6)(12)所描述的非线性系统模型对故障偏差值进行估计，本文结合滚转角和俯仰角无法直接测量得到的实际应用情况，考虑到传感器的六个分量可能同时出现的多个偏差故障，所设计的四旋翼飞行器传感器偏差故障检测与诊断系统结构如图2所示。

整个BFDD系统由偏差故障的检测与隔离、故障偏差值的估计两部分构成。BFDD系统的输入包括控制器输出、传感器测量值以及滚转角/俯仰角估计值。系统通过加速度计故障观测器和陀螺仪故障观测器对传感器状态进行实时估计，一旦传感器的故障被检测到并隔离，便会激活与之对应的非线性自适应故障偏差观测器完成对故障偏差值的估计，得到的偏差估计值可有助于提升飞行器控制系统的容错能力，从而保证飞行器的稳定性与安全性。

图2 偏差故障检测与诊断系统结构Fig.2 Structure of bias fault detection and diagnosis system

3 基于滑模观测器的姿态角估计

将式(5)代入式(1)可得：

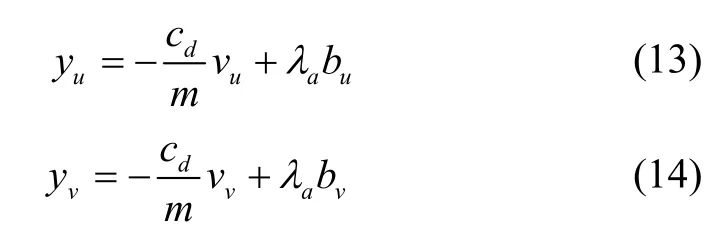
其中，yu和yv分别表示飞行器在机体坐标系下x方向和 y方向上的平移加速度测量值。分别对式(13)和式(14)进行求导运算，并结合式(2)有：

将式(15)和(16)中出现的正弦项作为系统动力学的未知输入。应用文献[15]中所提出的基于未知输入估计的滑模观测器方法，则有：

且参数uρ、vρ满足如下条件：

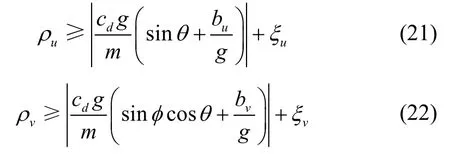
其中，uξ、vξ为小的正常数。利用式(15)～(18)，得到加速度计动态估计误差为：

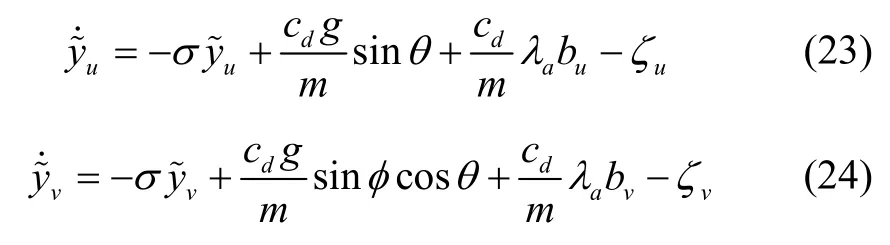
选取Lyapunov函数为：

对式(25)求导，并结合式(19)得到：

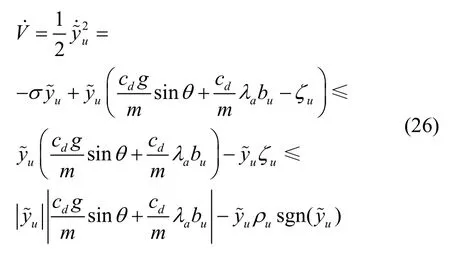
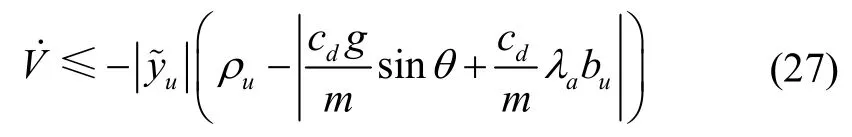
结合式(21)有：

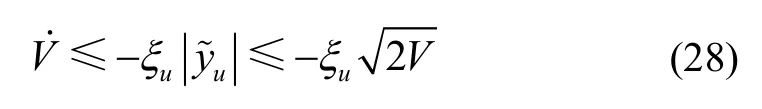
式(28)提供了滑模运动的可达性，在滑模运动中，由于式(17)中的信号uζ上的有限切换频率，我们有通常，俯仰角θ的变化比信号uζ的开关频率慢得多，有：

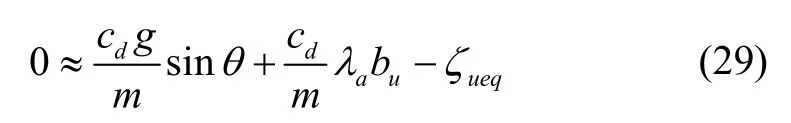
其中，ueqζ为保持滑模运动所需的等效输出误差注入信号，并表示在式(19)中定义的非连续分量的平均行为。可以通过使用低通滤波器来得到，即：

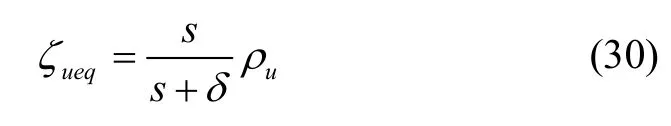
其中δ为一正常数。因此，未知的正弦项可估计为：

同样地，

其中，veqζ为保持滑模运动所需的等效输出误差注入信号。因此，通过使用式(31)(32)，在没有加速度计故障的情况下，可以产生对滚转角θ和俯仰角度φ的估计值为：

4 传感器的故障观测器设计

将如式(5)(6)所描述的传感器偏差故障模型代入四旋翼飞行器动力学模型有：

可以看出，加速度计偏差故障只出现在系统的位置和速度的动力学方程中，陀螺仪偏差故障只出现在系统的欧拉角和角速率动力学方程中。因此，可将这两类传感器偏差故障分别进行故障的检测与诊断。

4.1 加速度计故障观测器

根据式(35)，得到四旋翼飞行器的质心运动方程为：

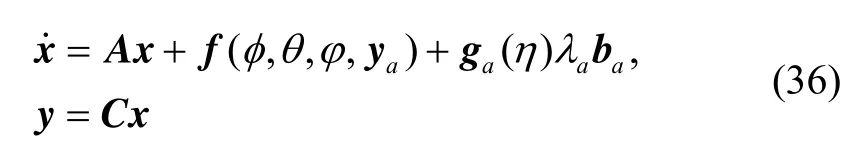
设计如下加速度计故障观测器：

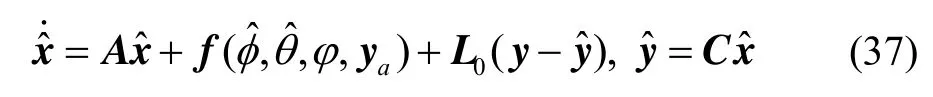
且渐进稳定。{A, C}完全能观测。

当att＜时，加速度计并未发生故障，在有限时间内俯仰角和俯仰角的估计值与实际值非常接近，也就意味着Δ0→f，因此有：

利用三角不等式，并结合式(38)(39)有，加速度计输出估计误差满足：

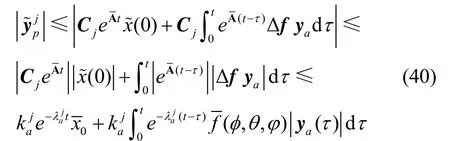
其中，jC表示矩阵 C的第 j列（j=1,2,3），常数均大于0，且因此，得到加速度计故障检测与隔离的阈值为：

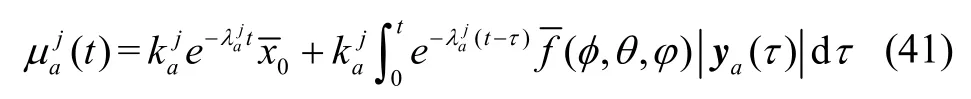
4.2 陀螺仪故障观测器

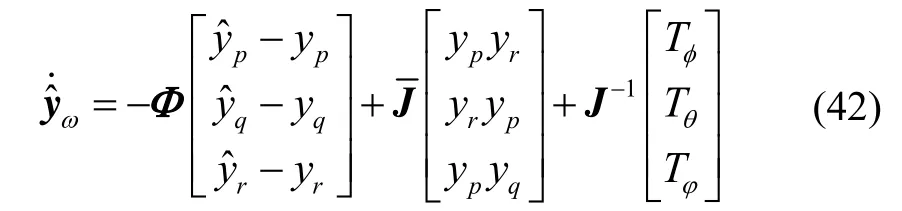
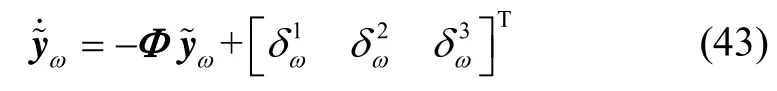
在假设模型误差有界的前提下，陀螺仪输出估计误差满足：

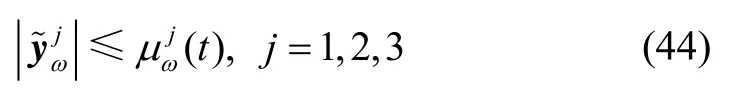
当ttω＞时，陀螺仪发生故障，则陀螺仪输出的估计误差满足：

5 传感器故障偏差观测器

5.1 加速度计故障偏差观测器

设计用以估计加速度计故障偏差值的非线性自适应观测器为：

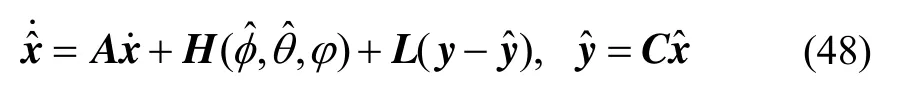
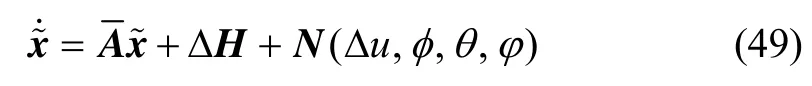
当加速度计传感器发生偏差故障，并在Ta＞ta时刻被检测到，则惯性坐标系下的速度估计误差为：

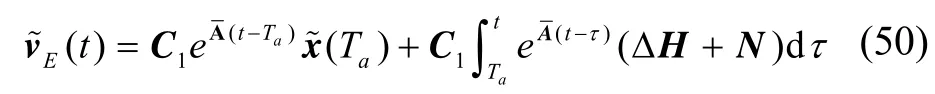
利用三角不等式有：

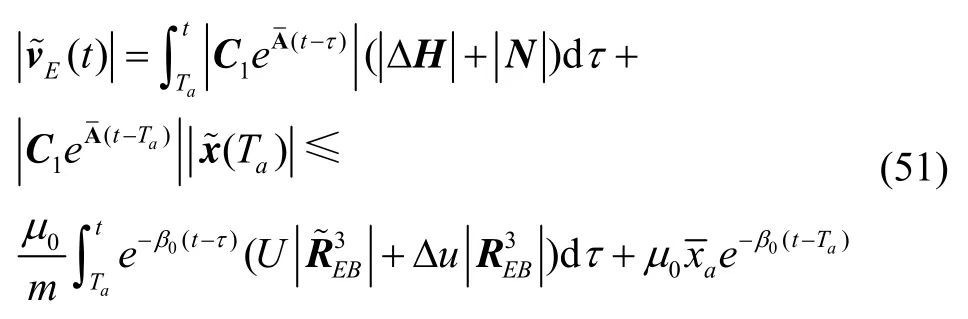
其中，μ0和β0均为正常数，且为状态估计误差初始值的上界，即

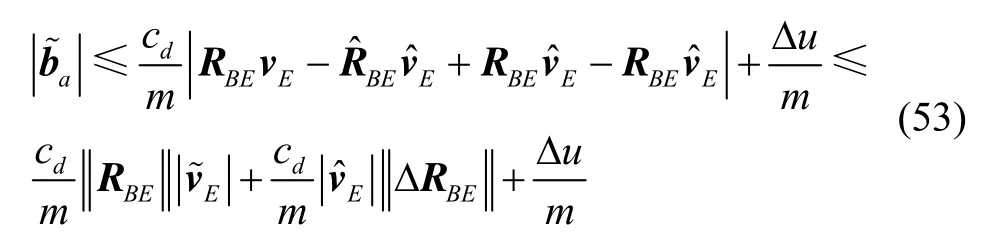
5.2 陀螺仪故障偏差观测器

根据式(33)～(35)，基于Lyapunov方法设计陀螺仪故障偏差观测器为：

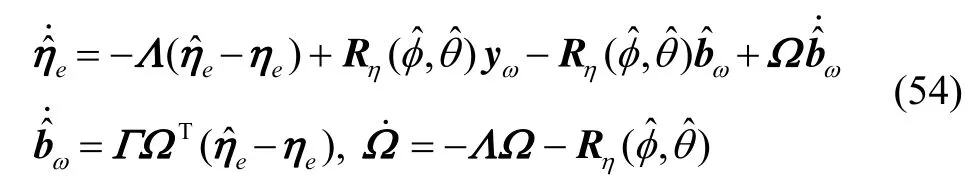
假设陀螺仪传感器在tω时发生偏差故障，在Tω时刻检测到故障，且定义为了保证参数的收敛性，对于在任意时，滤波器需满足如下条件：

其中，常数α1＞0，α0＞0和T0＞0。I3表示33×单位矩阵。定义欧拉角估计误差陀螺仪故障偏差的估计为

若陀螺仪在tω时刻发生偏差故障，在Tω时刻故障被检测到，在任意t＞时，在满足式(55)给定的条件下，则由式(54)表示的偏差故障观测器中所有信号均有界，且陀螺仪故障偏差的估计值收敛于零[16]。

6 实验研究

整个实验平台系统主要由课题组设计开发的四旋翼飞行器、地面站以及Vicon运动捕捉系统组成。搭建的室内实验平台系统结构框图如图 3所示。Vicon运动捕捉系统以 1 Hz的采样频率获取四旋翼飞行器飞行过程中的姿态和位置数据信息，并通过 TCP/IP协议将数据传输到地面站，作为实验中姿态和位置信息的参考值。地面站通过远距离射频模块XTend与飞行器相连接，从而实现数据快速可靠的传输与参数的在线调整。四旋翼飞行器的基本参数如表1所示。

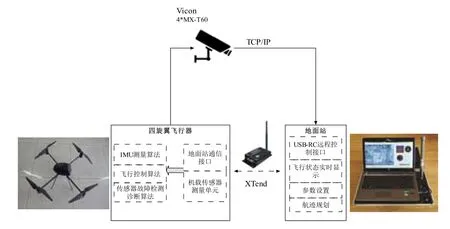
图3 实验平台系统结构框图Fig.3 Structure block diagram of experimental system

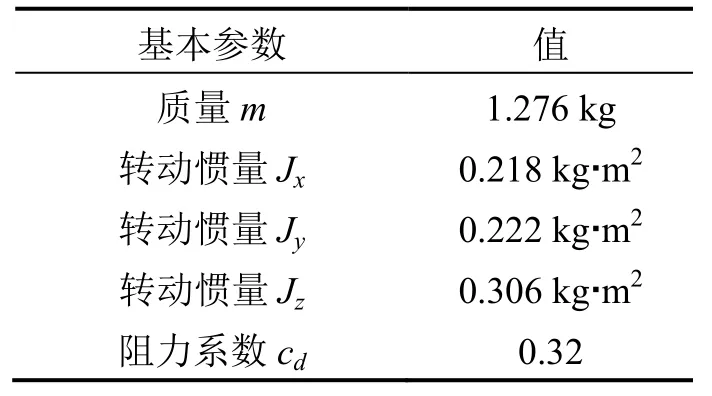
表1 四旋翼飞行器参数Tab.1 Parameters of quadrotor aircraft

在室内条件下，四旋翼飞行器按照既定半径为1m的圆形轨迹飞行过程中，来验证本文所设计的故障诊断方法的有效性。其中，用于估计姿态角的滑模观测器参数取值分别为：故障观测器增益矩阵的取值分别为：式(4)中表示的模型误差上界分别取和通过加速度计偏差故障、陀螺仪偏差故障以及加速度计和陀螺仪同时发生偏差故障的实验来验证本方法在单个和多个故障情况下的有效性。

6.1 加速度计偏差故障实验

在t = 30 s时，加速度计引入人为设定的故障偏差ba= [−0.45, 0.4, 1.2]T(m/s2)，姿态角的前后估计结果如图4所示。由图4可知，在加速度计偏差故障发生前后系统均能较为精确的实现对姿态角的估计。值得注意的是，在30～32 s之间，姿态角的估计值与测量值之间误差仅出现了短暂的波动，这与本文所提出的姿态估计算法仅利用机体坐标系下x和y方向的加速度信号有关。

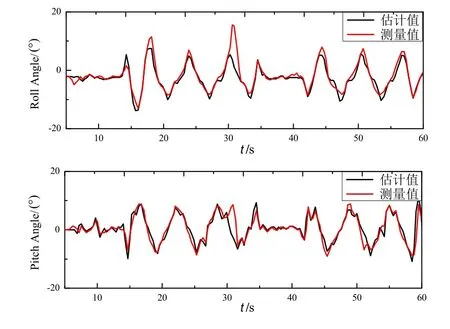
图4 引入ba后的滚转角和俯仰角估计曲线Fig.4 Estimation of roll angle and pitch angle with ba

图5 引入ba后的故障诊断残差Fig.5 The diagnostic residuals with ba

在引入故障偏差ba后，所设计故障观测器对故障残差诊断的实验结果如图5所示。图5(a)为加速度计故障残差诊断结果，加速度计故障观测器在引入故障偏差ba后，诊断残差超过检测阈值，加速度计偏差故障被检测到。图5(b)为陀螺仪故障残差诊断结果，诊断残差并未超过检测阈值，陀螺仪无偏差故障。

在检测到加速度计偏差故障之后，便会激活与之对应的故障偏差观测器，估计故障偏差的实验结果如图6所示。在30 s处发生偏差故障ba后，加速度计故障偏差观测器能够快速估计得到故障偏差ba，且估计误差有界。显然，所设计的加速度计故障偏差观测器能够准确估计并跟踪故障偏差ba，其有效性得以验证。

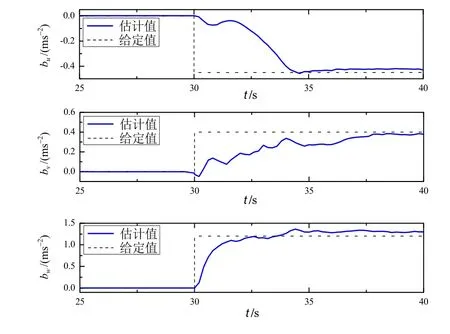
图6 加速度计故障偏差估计曲线Fig.6 Acceleration bias fault estimation

6.2 陀螺仪偏差故障实验

在 t = 30 s时，陀螺仪引入人为设定的故障偏差bω= [5, 7, 10]T(°/s)，姿态角的前后估计结果如图7所示。

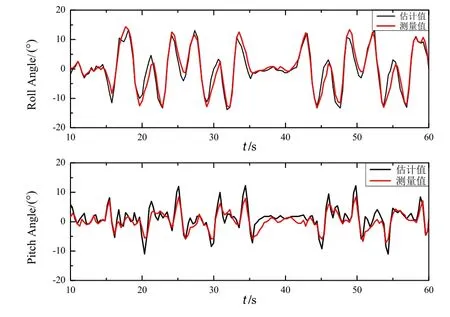
图7 引入bω后的滚转角和俯仰角估计曲线Fig.7 Estimation of roll angle and pitch angle with bω

由图7可知，在故障发生前后系统均能较为精确的实现对姿态角的估计。与加速度计故障情况不同的是，姿态角的估计值与测量值之间误差并未出现短暂的波动。

在引入故障偏差bω后，所设计故障观测器对故障残差诊断的实验结果如图8所示。图8(a)为加速度计故障残差诊断结果，诊断残差未超过检测阈值，加速度计无偏差故障。图8(b)为陀螺仪故障残差诊断结果，陀螺仪故障观测器在引入故障偏差bω后，诊断残差超过检测阈值，陀螺仪偏差故障被检测到。

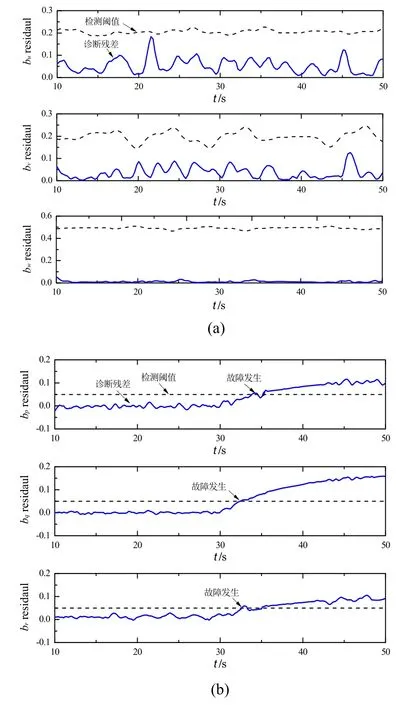
图8 引入bω后的故障诊断残差Fig.8 The diagnostic residuals with bω

在检测到陀螺仪偏差故障之后，便会激活与之对应的偏差观测器，估计故障偏差值的实验结果如图 9所示。在30 s处发生偏差故障bω后，陀螺仪故障偏差观测器能够在10s之后完成对故障偏差ba的估计，且接近给定值。所设计陀螺仪故障偏差观测器能够准确估计并跟踪故障偏差bω，其有效性得以验证。

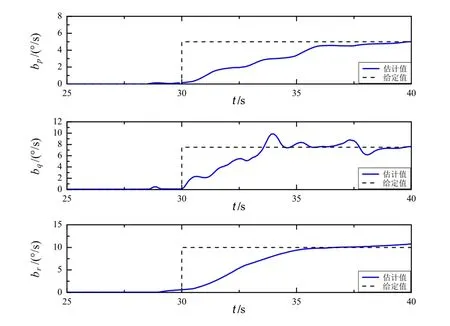
图9 陀螺仪故障偏差估计曲线Fig.9 Gyroscope bias fault estimation

6.3 多故障实验

在时间t = 30 s时，同时引入加速度计故障和陀螺仪偏差故障，用以验证同时对多故障进行诊断与估计的能力。引入的偏差故障大小分别为ba= [5.5, -4.5, 1.2]T(m/s2)和bω= [4.5, 3, 5]T(°/s)。姿态角的估计结果如图10所示。

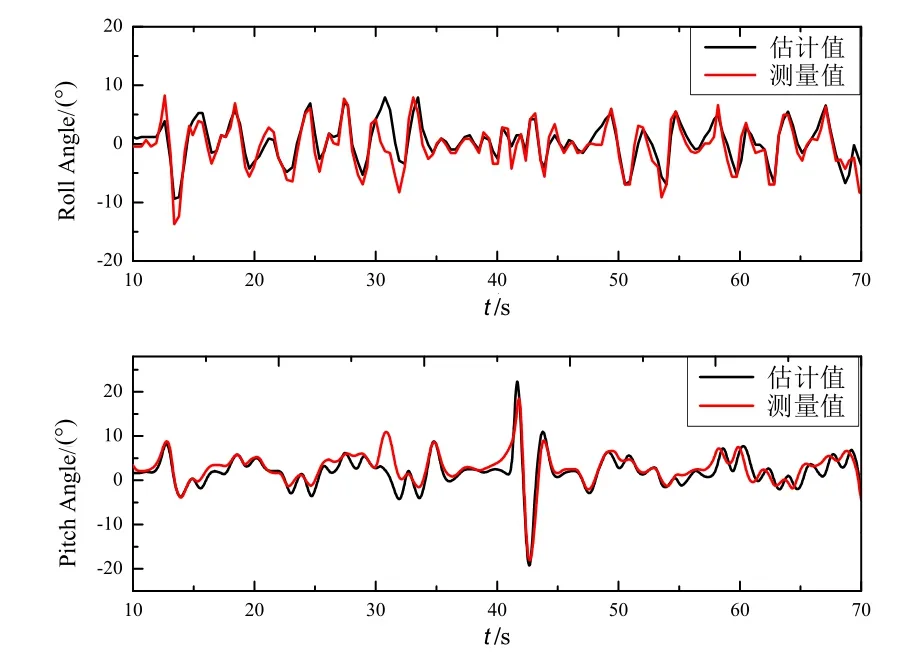
图10 多故障时滚转角和俯仰角估计曲线Fig.10 Estimation of roll angle and pitch angle with multiple simultaneous faults

加速度计和陀螺仪同时发生偏差故障，通过故障观测器对故障残差进行诊断的实验结果如图11所示。由图可知，在多故障发生后，诊断残差均在较短时间内超过各自的检测阈值，从而检测到同时发生的偏差故障。在多故障条件下，验证了本文方法的对多故障检测的有效性。

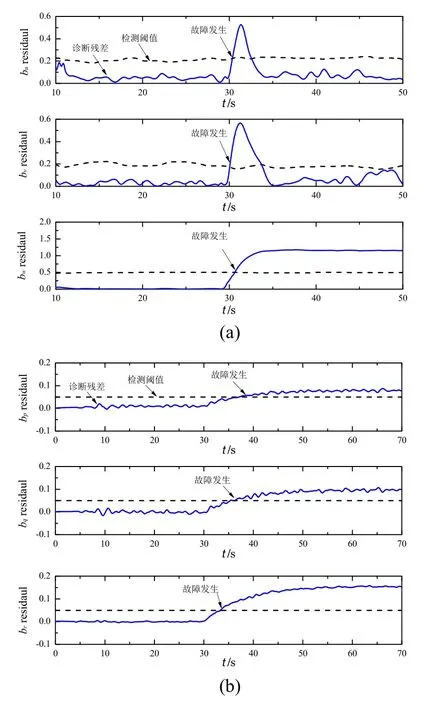
图11 多故障时故障诊断残差Fig.11 Diagnostic residuals with multiple simultaneous faults

在检测到加速度计和陀螺仪偏差故障之后，便会激活与之对应的偏差观测器，在多故障条件下，估计故障偏差的实验结果如图12所示。图12(a)为估计加速度计故障偏差的实验结果，图12(b)为估计陀螺仪故障偏差的实验结果。由图可知，本文设计的加速度计故障偏差观测器和陀螺仪故障偏差观测器均能够在5 s之内准确估计和跟踪各自的故障偏差值，且估计误差有界。

图12 多故障时故障偏差估计曲线Fig.12 Bias fault estimation in the case of multiple simultaneous faults

7 结 论

为了提高四旋翼飞行器的容错能力，保证其安全可靠地完成飞行作业任务，本文针对四旋翼飞行器多传感器偏差故障的诊断问题，在飞行器姿态角无法直接测量得到的前提下，提出一种基于姿态角估计的四旋翼飞行器多传感器偏差故障诊断方法，并构建出适用于四旋翼飞行器的多传感器偏差故障诊断系统。数值仿真和实际飞行实验结果表明，所构建的故障诊断系统可快速地实现对多传感器偏差故障的检测与隔离，对故障偏差值的准确估计与跟踪，进而有效地提高四旋翼飞行器的可靠性与安全性。