一种用于振动陀螺零偏抑制的复合融合算法

刘 宇，司学迁，路永乐，邸 克，向高军，李俊林

（重庆邮电大学 光电信息感测与传输技术重庆市重点实验室，重庆 400065）

陀螺仪是惯性导航技术中的关键部件，被广泛地应用于航天、军事、航海等领域[1]。陀螺仪的性能是影响惯导系统性能的关键因素之一，因此提高陀螺仪的性能具有非常重要的意义,其中零偏稳定性是陀螺仪的一项重要性能指标[2]。

振动陀螺仪信号包含噪声的主要原因有以下几点：陀螺仪自身存在漂移误差；硬件采集信号时产生的误差；系统中各个电子元器的之间的干扰；系统中电源与板卡之间的相互电磁作用。其中，陀螺仪自身漂移产生的噪声是原始采集信号噪声的最主要组成部分，环境温度是影响陀螺仪自身漂移的重要因素，本算法主要用于抑制不同温度下陀螺自身漂移误差。

由于噪声一般由频率1000 Hz以上的高频信号构成，而姿态角的更新频率一般在1000 Hz以下，因此很多去噪研究是根据傅里叶变换来展开的。但是由于陀螺仪的噪声信号中经常会出现突变和奇异信号，这会大大加大傅氏变换的计算难度。为解决上述问题，小波变换被广泛应用于此类信号处理中。但是小波变换在对高频信号做阈值处理时，如果采用软阈值处理，会导致滤波效果不佳[3]；如果采用硬阈值处理，则会导致部分有用信号被舍弃[4]。针对噪声特性的不确定性，很多研究者也引入了最小二乘法对其进行拟合估计[5]。但是直接使用最小二乘法进行拟合会受到原始信号中噪声的影响，使得拟合效果不尽如人意。

综上所述，本文首先应用小波分析法对原始信号进行分解，并对分解后的信号进行软阈值处理，其次将处理后的信号合成，得到粗糙去噪信号；然后采用遗忘因子的递推最小二乘，对于粗糙去噪信号采用推广递推最小二乘进行最优估计，最终得到较理想去噪信号。在常温25℃、高温80℃、低温-40℃下，利用本实验室自主研发的高精度三轴振动陀螺实验表明：经本融合算法处理后，振动陀螺三个轴向的零偏稳定性均有显著提高。

1 小波降噪原理

小波变换可用于弥补傅里叶变换时域局部化特征差、不适用于突变信号的处理等。由于小波变换具有母函数类型丰富、紧支性等优势，近年来被广泛应用于具有突变和奇异情况的非平稳信号的研究中[6-9]。本文基于小波分析理论，结合采集的陀螺仪信息特点，采用软阈值小波变换阈值法对测量的陀螺仪信息进行观测。

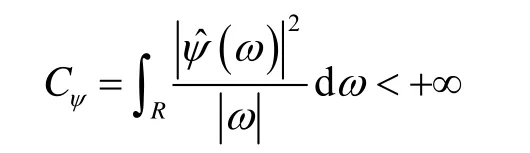
于是有：

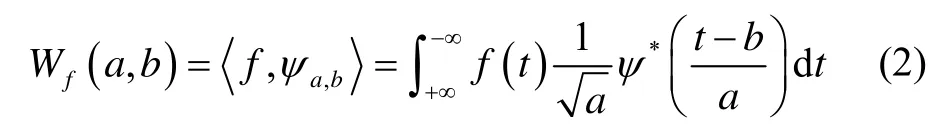
2 含遗忘因子的推广递推最小二乘法拟合

在陀螺仪实际工作中，噪声信号具有不确定性，并且常见突变和奇异信号，卡尔曼滤波使用在此场景下，常常会失去优越性。经过推导[11]，含遗忘因子的递推最小二乘法数学表达式为：

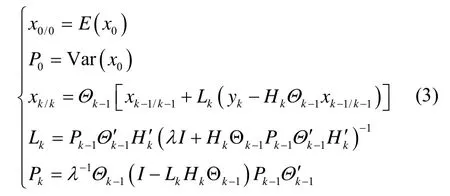
其中，λ为遗忘因子，其取值范围为（0,1]；λ取值的大小负相关于参数变化的快慢，当λ=1时，即为基本递推最小二乘法。λ的取值对于拟合情况很关键，可由自适应算法得到。

3 小波分析和推广递推最小二乘的融合去噪算法设计

3.1 小波滤波在陀螺仪中的应用

假设陀螺仪原始测量信号的数学模型如下：

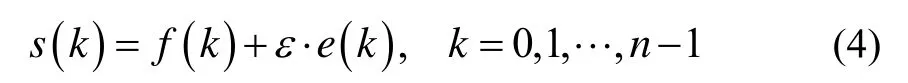
其中，s(k)是陀螺仪原始测量信号，f(k)是无偏信号，ε是噪声系数的标准差，e(k)是噪声。

针对陀螺仪零偏测量值，噪声一般集中于高频信号中，而在低频信号中几乎不存在。对原始测量信号s（k）进行多尺度分解，小波分解在陀螺仪信号处理应用中的优劣取决于小波母函数的选取和阈值函数的选择，常见的阈值函数有硬阈值处理和软阈值处理，其数学表达式分别如下：

硬阈值处理：

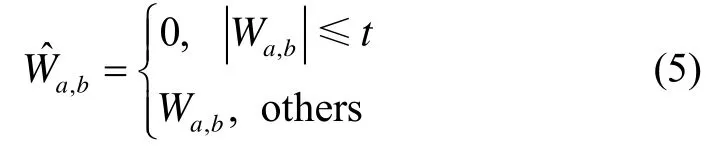
阈值处理：

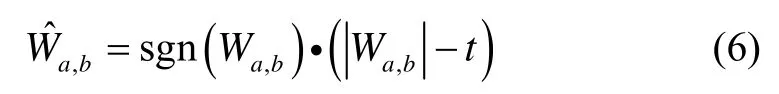
本文根据陀螺仪数据特征对低频分量进行保留处理，对高频信号进行软阈值处理，然后利用离散小波逆变换对处理后的分量进行重构，得到s1(k)，从而达到粗滤波效果。

3.2 小波分析和推广递推最小二乘的融合去噪算法

基于小波分析和推广递推最小二乘的融合算法的思想是：对原始测量信号 s(k)k∈z进行离散小波变换，经过m层小波分解得到高频分量H1、H2、…和低频分量L1、L2、…，对各分量进行软阈值处理，再通过离散小波逆变换得到重构信号 s1(k)k∈z，该信号为粗滤波效果，将其作为递推最小二乘法的初始值，即

融合去噪算法流程图如图1所示。

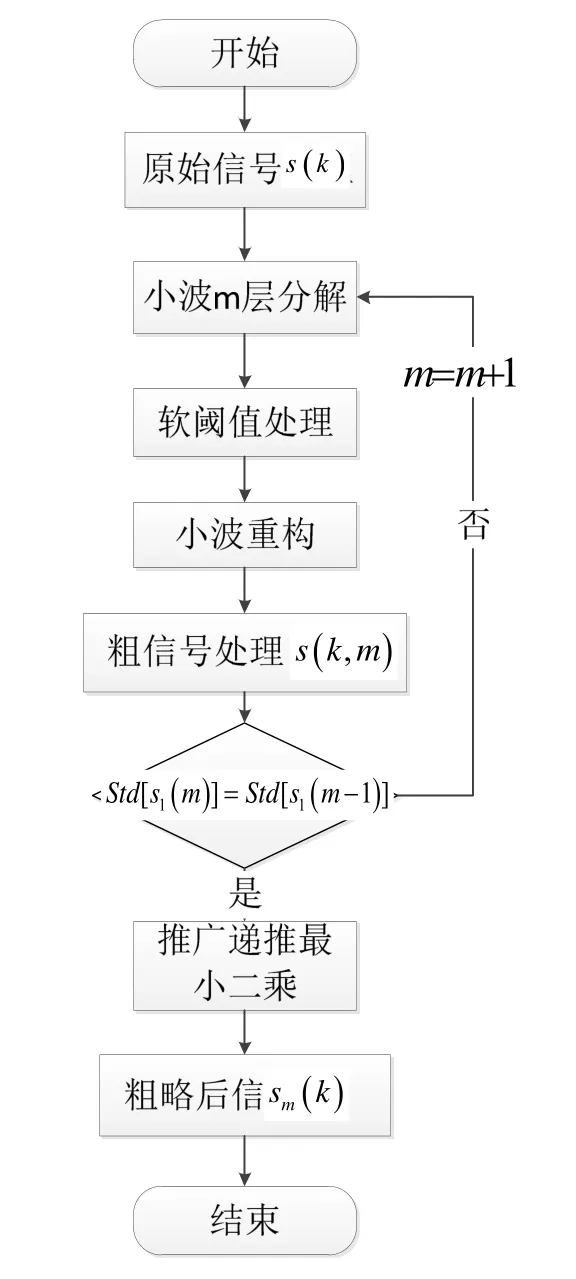
图1 融合去噪算法流程图Fig.1 Flow chart of fusion denoising algorithm

根据陀螺仪数据具有良好连续性的特性，本研究中选择了具有紧支性和良好连续性和对称性的 Sym8小波作为母函数ψ(t)。小波分解的过程实则为不同尺度因子 a和不同缩放因子 b下计算最大相关因子的过程，其中

首先使小波函数与陀螺仪原始测量数据最前端数据进行对比，计算相关因子Ca,b(1,1)；再令小波函数平移2j个单位长度，其中 j为正整数，遍历整个信号数据进而计算出[Ca,b(1,1),Ca,b(1,2),…,Ca,b(1,k)…]；然后将小波函数以2j倍进行缩放，其中j为正整数且1jm＜≤，平移缩放后的小波函数遍历整个过程，同理可得即可得相关因子矩阵：

本研究中融合算法的最小二乘目标函数为：

其中，s1是观察值，x为拟合值，即优化目标为最小化 s1和x之间的距离平方和。此时，可将目标函数划归为矩阵求解问题，然后求导后值为 0，从而得到极值，求解公式可抽象为公式(9)(10)：

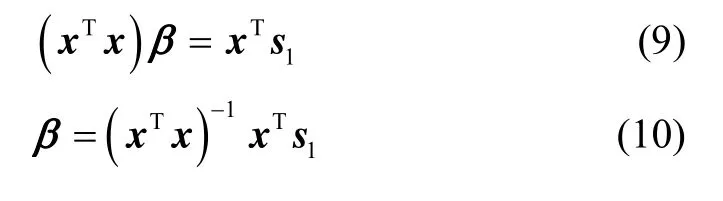
4 实验分析

由以上理论分析可知，本融合算法能够得到较好的滤波效果。为了验证本算法的可行性，使用本实验室自主研发的三轴振动陀螺仪对本融合算法进行实验验证，振动陀螺所使用的数字处理器为DSP C6000系列处理器，其主频可达 456 MHz，姿态角算法周期为0.5 ms。测试平台如图2所示，本测试平台由双轴测试转台机械台体、测控系统和高低温箱构成，双轴测试转台速率精度及平稳性可达10-4(360°平均)；高低温箱精度可达温度波动度小于±0.5℃；实验室自主研发的三轴振动陀螺仪分辨率为0.005 (°)/s，测量范围为300 (°)/s，工作温度为−50℃～+125℃。

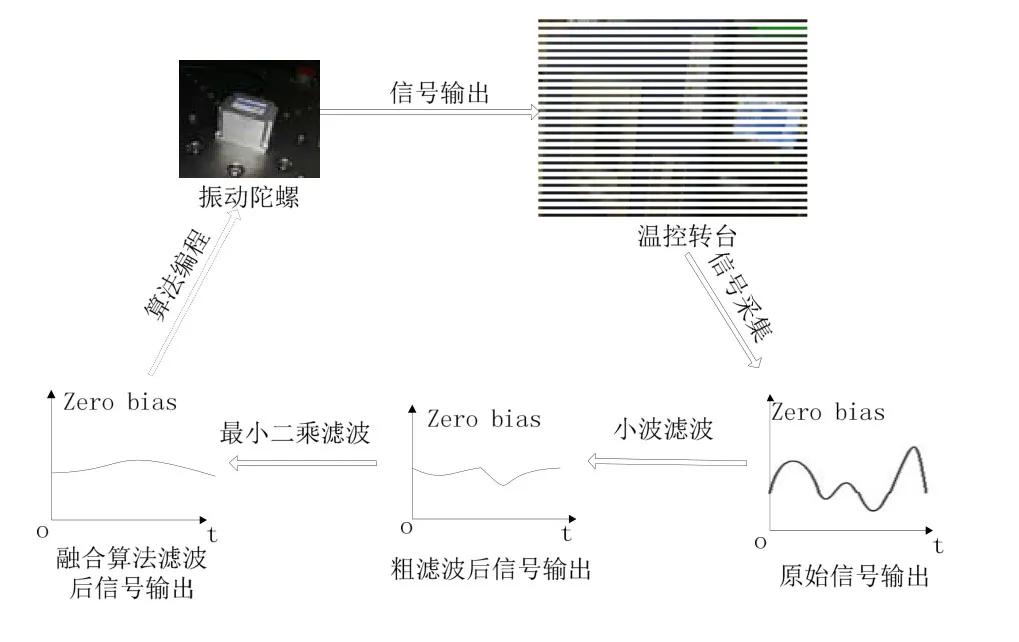
图2 实验平台与实验流程示意图Fig.2 Experimental platform and experimental flow diagram

实验中将陀螺仪置于常温25℃、高温85℃、低温−40℃采样环境中，持续放置1 h后通电采样。在转台未使能状态下，持续采集陀螺仪静态数据30 min，将数据以每10 s为基准得到基本取样点，30 min内可得到180个取样点，作为原始信号数据。本研究实验中将原始信号数据、经过传统小波粗滤波数据和经过本研究融合算法滤波后数据使用Matlab绘制成图，实验中三类数据为50次测量值的平均值。图3～5依次表示为陀螺仪常温25℃、高温85℃和低温−40℃工作状态下的实时数据信息图。其中：图(a)表示 X轴数据信息，图(b)表示Y轴数据信息，图(c)表示Z轴数据信息，绿线代表原始数据，红线代表粗滤波数据，蓝线代表本研究中融合算法数据；实验中取样频率为2000 Hz。

如图3～5所示，可以明显看出在不同温度状态下，陀螺仪原始数据波形均具有很多噪声，粗滤波后的数据噪声有所抑制但不够显著，而经过本研究融合算法滤波后的数据趋于平缓，零偏稳定性有了明显改善。

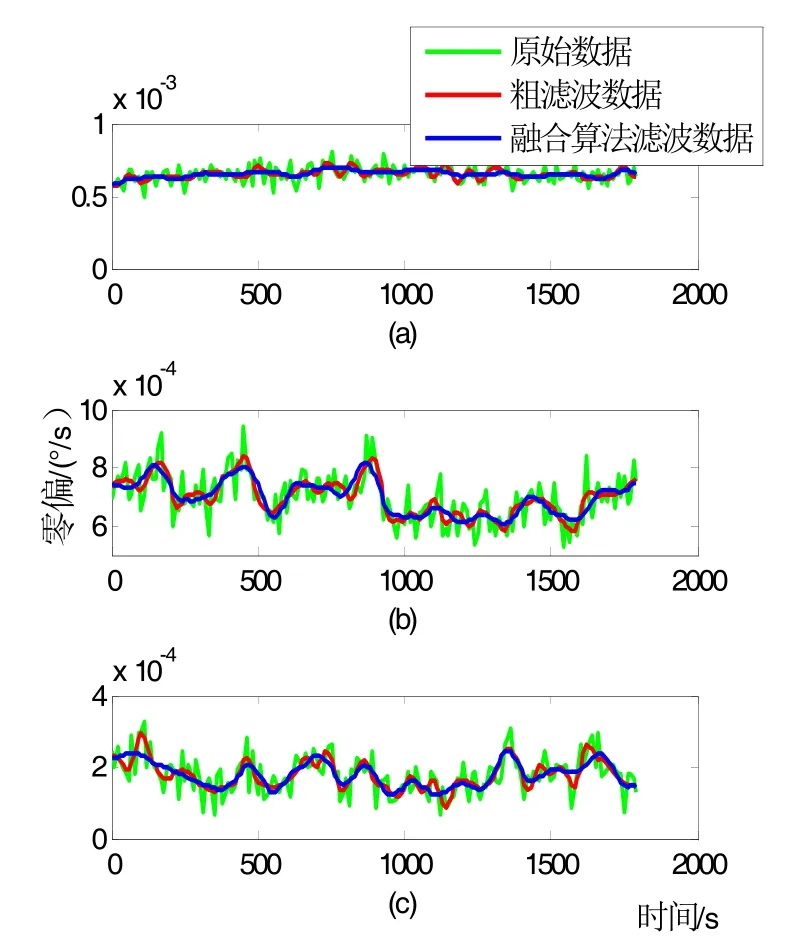
图3 陀螺仪在25℃工作状态下实时数据信息图Fig.3 Real-time data information diagram of gyroscope working at 25℃

图4 陀螺仪在85℃工作状态下实时数据信息图Fig.4 Real-time data information diagram of gyroscope working at 85℃

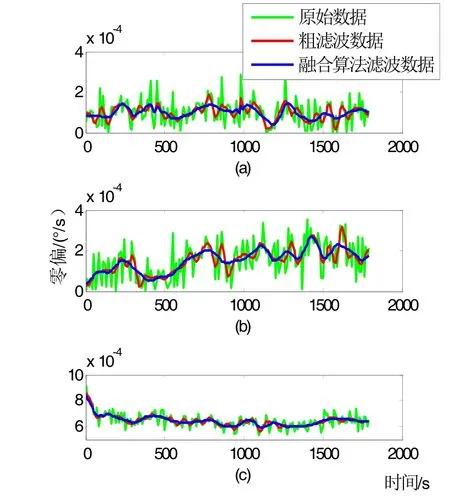
图5 陀螺仪在−40℃工作状态下实时数据信息图Fig.5 Real-time data information diagram of gyroscope working at −40℃

需要注意的是：不同温度下，融合算法中小波分解的层数m不一定一致，当m达到一定级别后，m+1层分解与m层分解数据标准差基本相等，此时便不需要再增加m的值。

不同工作状态下，陀螺仪三个轴向三组数据零偏稳定性数据对比如表1所示。

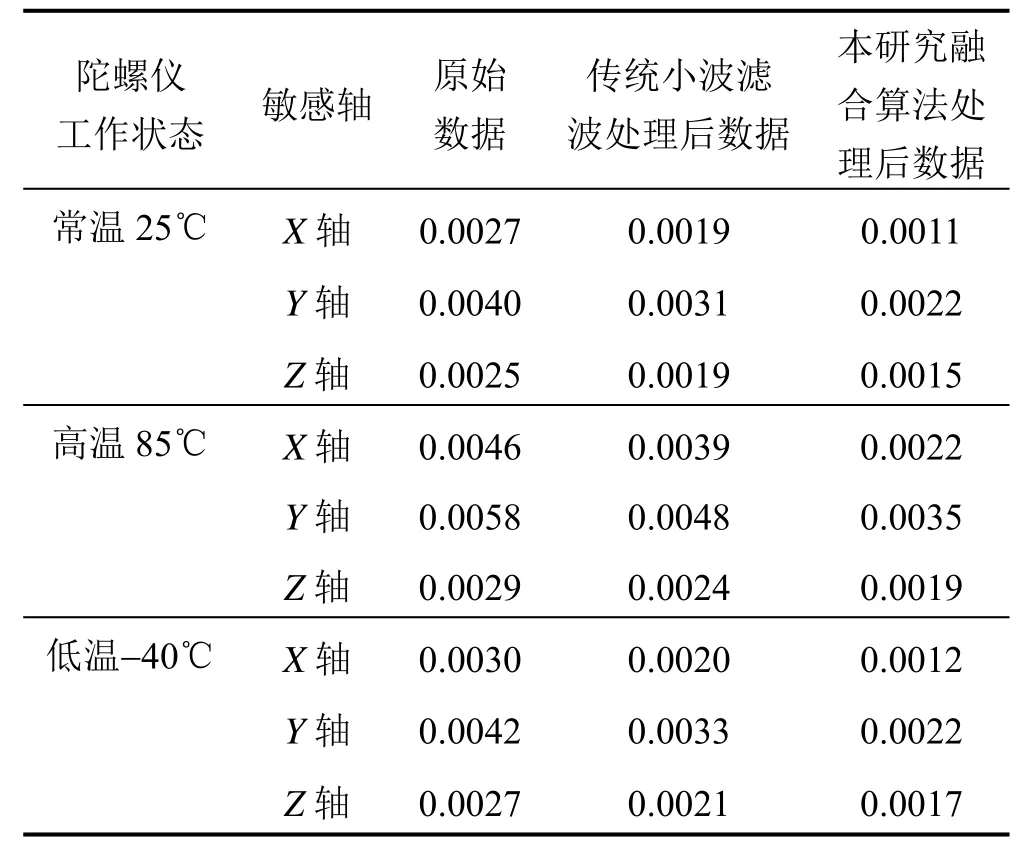
表1 陀螺仪三个轴向三组数据零偏稳定性数据Tab.1 Three sets of triaxial data zero offset stability of the gyroscope (°/s)

从以上图表中可以明显看出，经本研究融合算法处理后的陀螺仪三个轴向数据的零偏稳定性相较于原始数据和经传统小波滤波处理后数据均有提高，为了定量地表示本设计对陀螺仪零偏稳定性的提高程度，本文定义性能提高度（S）：

其中，std0代表原始数据标准值，stdm表示经过处理后数据的标准差值。

传统小波滤波和本研究融合算法性能提高度数据对比如表2所示。

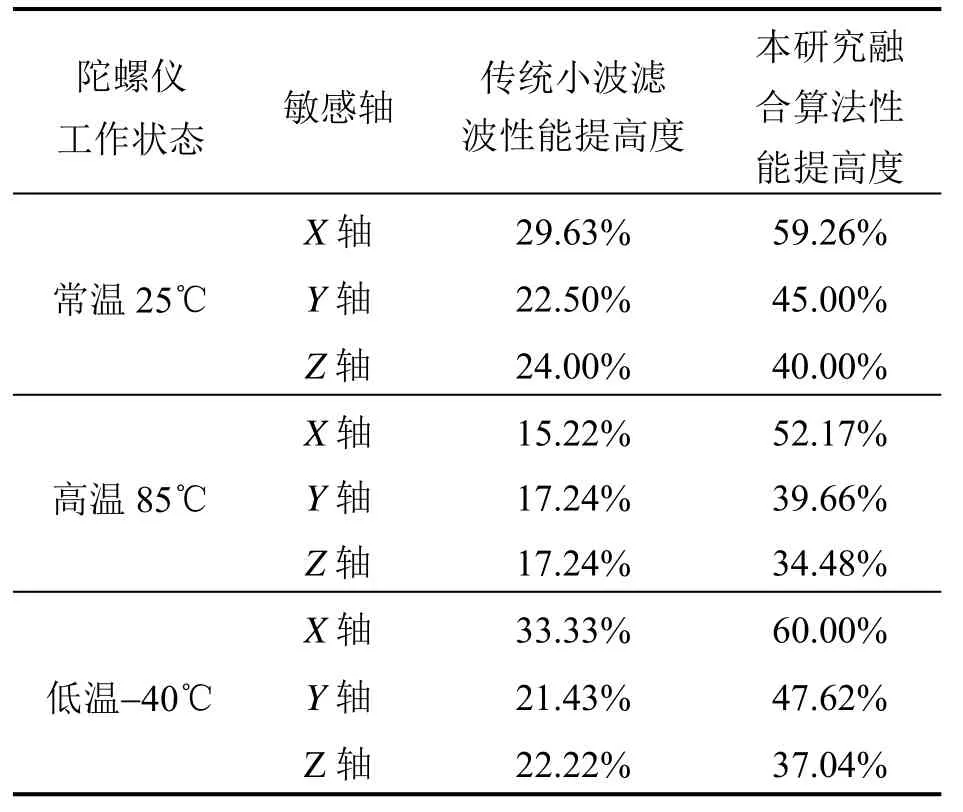
表2 传统小波滤波和本研究融合算法性能提高度Tab.2 Comparison on performance improvements between traditional wavelet filter and the proposed fusion algorithm

通过表2数据可知，针对本实验室独立研发的陀螺仪，基于传统小波滤波后的数据性能提高度为20%左右，而基于小波分析和推广递推最小二乘拟合融合算法处理后的数据性能提高度在常温 25℃下可达到了40%以上，在高温85℃下可达35%左右，在低温下可到 37%以上；不同工作环境中，本融合对于 x轴的零偏性能影响最大，性能提高度均达到了 50%以上。由此可知本研究中的融合算法可以显著提高陀螺仪零偏稳定性。

5 结 论

零偏稳定性是衡量陀螺仪优劣的重要指标。小波分析和推广递推最小二乘融合算法是将原始陀螺仪零偏数据经过多层次小波分解后，然后进行软阈值处理，紧接着进行小波重构得到粗滤波数据信息，再通过推广递推最小二乘法对粗滤波数据进行拟合，最终得到较理想的陀螺仪零偏信息。通过实验验证可得，在常温25℃、高温85℃、低温-40℃不同工作条件下，经过小波分析和推广递推最小二乘拟合融合算法处理后的三个轴向数据相比于原始数据稳定性提高了40%左右，相较于传统小波分析所得数据稳定性提高了 20%左右。由实验分析可得，本研究算法滤波效果较为明显。