基于位置约束的两轮驱动机器人路径跟踪控制方法

朱欣华，王 健，郭民环，姚速瑞，苏 岩

（南京理工大学，南京 210094）

目前，两轮驱动机器人广泛应用于工业生产、仓储转运以及智能家居等多个领域，在节约人力成本的同时，能够有效提高工作质量[1-3]。两轮机器人的运动控制对其性能有着很大的影响[4]。运动控制主要包括路径规划和路径跟踪两方面内容。路径规划是根据机器人的任务要求以及所处的环境信息通过特定的算法计算搜索出最优路径，然后再对计算得到的最优路径进行跟踪，而准确地进行路径跟踪，是两轮驱动机器人顺利完成任务的基础[5]。由于两轮驱动机器人属于欠驱动系统，较难控制，目前大部分实际应用的两轮驱动机器人的路径跟踪控制都是基于双闭环的电机控制，内环是电流环，外环是速度环，每个电机单独控制[6]。这类方法通常有一定的局限性，由于没有引入位置信息，若两轮机器人的初始位置与期望路径的初始位置存在较大偏差，或者两轮机器人在行驶过程中受外力影响发生横向偏移时，两轮机器人将无法对期望路径进行跟踪。同时，目前对于两轮驱动机器人运动控制的研究较多地停留在理论研究阶段，对于控制方法的实际验证较少[7]。

本文针对两轮驱动机器人的路径跟踪问题，提出一种新的控制方法。通过左右轮的双闭环控制来约束两轮机器人的速度和位姿，在此基础上，在期望路径附近建立矢量场，引入位置约束，促使两轮机器人在偏离期望路径时能够快速回归，完成路径跟踪任务。同时搭建了两轮驱动机器人硬件实验平台，分别对直线路径和曲线路径进行跟踪，验证双闭环控制的有效性。在此基础上通过外力使两轮机器人偏离期望路径后再进行路径跟踪，以验证在存在位置误差时矢量场法的有效性。最后对通过路径规划算法计算出的路径进行跟踪，验证本文提出的路径跟踪控制方法的实用性和有效性。

1 两轮驱动机器人运动学模型

两轮驱动机器人在二维平面的运动可以简化为平面刚体运动。其运动完全靠两个驱动轮的转速来控制[8]。在路径跟踪控制之前，先要对两轮驱动机器人的线速度v和角速度ω的信息进行融合，分别求出加在闭环驱动器上左右轮的期望速度，然后再对两轮的速度进行闭环控制。

两轮驱动机器人的机械结构由两个驱动轮、一个随动轮以及机器人主体组成。随动轮仅在运动失衡时起支撑作用，在运动学方程中可以忽略不计，其简化模型如图1所示。在全局坐标系（O, X, Y）中，两轮机器人的位置（图中的点 M）可由向量表示，机器人的运动学方程表示为：

式中，ωl表示左轮角速度；ωr表示右轮角速度；R表示机器人驱动轮半径；D表示两驱动轮之间的距离。

参考机器人位置（图中的点 N）由向量 pr=表示，如图1所示，以两轮机器人M为参考建立局部坐标系 (o, i, j)，其中局部坐标系原点o为机器人两驱动轮轮重心连线的中点，i方向为机器人速度正方向。机器人运动的误差矢量可表示为：

两轮驱动机器人的位置可以由以下方程表示：

式中，ΔΦr和ΔΦl分别为采样时间内两轮驱动机器人左右编码的角位移；Δs为采样时间内机器人的移动位移；Δθ为采样时间内机器人的移动角度。

图1 两轮驱动机器人运动模型示意图Fig.1 Schematic diagram of motion model of two-wheel-drive robot

基于两轮驱动机器人运动模型的路径跟踪控制问题主要是使机器人系统在任意初始误差下，确定两轮驱动机器人的输入控制vc和ωc，从而跟踪参考位姿和参考输入

2 路径跟踪控制方法

针对两轮驱动机器人的路径跟踪问题，通过给定驱动电机不同的速度参数来控制两轮差速驱动机器人的位姿和速度，从而实现两轮驱动机器人的直线、转弯或旋转等不同的运动方式。首先建立左右轮的双闭环PID控制器，通过约束两轮驱动机器人的速度和位姿的方式来跟踪期望轨迹，在此基础上，在期望路径附近建立矢量场，引入位置约束，促使两轮驱动机器人在偏离期望路径时能够快速回归。

2.1 双闭环PID控制器

PID控制是一种最通用的控制方法[9]。大多数反馈回路用该方法或其较小的变形来实现控制。常规的PID控制系统主要由被控对象以及控制器两个部分构成[10]。本文所设计的控制算法的核心思想是通过双闭环PID控制器来调节两轮驱动机器人左右两轮的转速，从而对期望路径进行跟踪，其原理如图2所示。

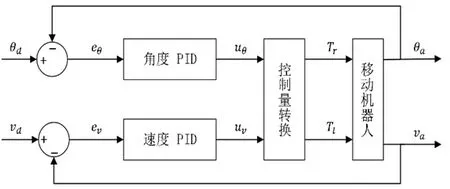
图2 两轮驱动机器人运动控制算法原理图Fig.2 Motion control algorithm schematic of two-wheel-drive robot

控制算法包含两个PID控制器。其中，θd和vd分别为两轮驱动机器人的期望航向角和期望线速度；θa和 va分别为两轮驱动机器人的实际航向角和实际线速度。在角度环PID控制器中，输入值为航向角误差eθ，输出值为uθ，方程如下：

式中，Kpθ为角度环比例项系数，Kiθ为角度环积分项系数，Kdθ为角度环微分项系数。求解出的 uθ（t)用来修正两轮驱动机器人在运行过程中的航向误差。

在速度环PID控制器中，输入值为两轮驱动机器人两驱动轮连线中点线速度误差 ev，输出值为 uv，方程如下：

式中，Kpv为速度环比例项系数，Kiv为速度环积分项系数，Kdv为速度环微分项系数。求解出的 uv（t)用来控制两轮驱动机器人在运行过程中的行驶速度。

传统以轮距中点为参考对象的两轮驱动机器人的控制通常是通过维持作为参考对象驱动轮角速度不变，而通过调整另一个轮的角速度来调节航向角，这种控制方式调节不够灵活，在转角比较大的环境中具有局限性[11]。而本文设计的控制方法，是通过速度环PID控制器求解出控制量 uv(t)来调节左右轮驱动电机的基础转速，然后通过角度环PID控制器求解出控制量uθ(t)来调节两轮驱动机器人的姿态。方法如下：

式中，Tr和 Tl分别为输入到右轮和左轮驱动电机的值，K为控制量到电机驱动模块的PWM值的转换系数。最终，通过对两轮驱动机器人左右轮的分别控制，实现两轮驱动机器人对预期轨迹的跟踪。

2.2 矢量场的建立

通过双闭环的PID控制器可以很好地对期望轨迹进行跟踪，由于没有引入位置约束，若两轮驱动机器人的初始位置与期望位置存在较大偏差或两轮驱动机器人在行驶过程中受外力因素位置发生偏离时，仅仅通过双闭环的PID控制器，无法使两轮驱动机器人回到预期的行驶路线。也就是说只依靠双闭环PID控制器只能保证机器人按照期望路径的形状行驶，无法保证两轮驱动机器人轨迹的绝对位置与期望路径重合。

针对以上问题，本文通过在期望路径附近建立矢量场的方法，引入位置信息，促使两轮驱动机器人在偏离期望路径时能够快速回归[12]。具体方法如下：

图3为两轮驱动机器人当前位置与预设轨迹示意图，P点为机器人的当前位置，P1为预设起点，P2为预设目标点，的长度为机器人的步长，机器人的期望路径可以看作由很多条该类型的线段组成。虚线y表示机器人当前位置P距离期望轨迹的距离，y有正负之分。建立矢量场是根据构建一个只考虑行驶方向的速度场，根据任一P点位置求解出行驶方向目标值。构建方法如下：

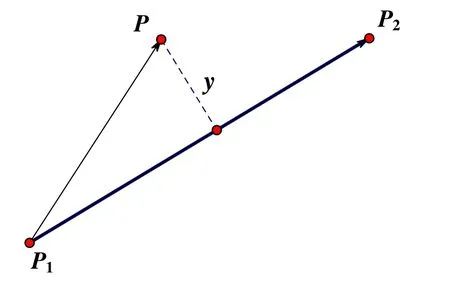
图3 两轮驱动机器人预设轨迹示意图Fig.3 Presupposition trajectory schematic of two-wheel-drive robot

其中，χd为行驶方向目标值，其为关于y的函数。χ∞是y很大时的行驶方向目标值，垂直并指向是值为正数的常量，用来调节arctan()ky·随y收敛到0的速度。由公式可以看出，当y很大，即两轮驱动机器人当前位置偏离期望路径很多时，求解得出的行驶方向目标值垂直指向期望路径当 y为 0，即机器人当前位置与期望路径重合时，求解得出的行驶方向目标值与期望路径平行。建立矢量场的仿真结果如图4所示，图中，点划线代表期望轨迹，箭头代表机器人在不同位置时求解出的期望行驶方向。

通过仿真结果可以看出，矢量场法在目标路径附近构建了一个全平面的矢量场，当两轮驱动机器人处于任何位置的时候，均可在矢量场的引导下回归到目标路径。可以通过调节式(14)中的 k值来改变回归的速度。由图4可以看出，当两轮驱动机器人距离目标路径较远时，求解出的期望行驶方向几乎垂直于目标路径，这样可以保证两轮驱动机器人快速回归。而当两轮驱动机器人接近目标路径时，求解出的期望行驶方向与目标路径之间的偏角逐渐变小，直至期望行驶方向与目标路径重合，这样可以保证两轮驱动机器人在回归过程中行驶轨迹圆滑。建立的矢量场很好地补充了双闭环PID控制器缺少位置信息的不足。

图4 矢量场法仿真结果Fig.4 Simulation results of vector field method

3 实验研究

3.1 实验平台及实验环境

图5为研究时所用的两轮驱动机器人平台，其主体由三个车轮和一个硬件平台组成。三个车轮中有两个为驱动轮，分别由两个PWM电机控制，另一个为万向轮，主要起支撑作用。硬件平台由一块Arduino uno R3开发板以及蓝牙模块等传感器组成，其中蓝牙模块主要用来实现机器人与上位机之间的无线通信。作为实验验证，由上位机将计算的结果发送给控制平台，通过控制两轮驱动机器人左右轮的转速来控制机器人运动。

在实际应用中，首先，根据实验用两轮驱动机器人平台的模型确定参考位姿，以两轮重心连线中点作为局部坐标系原点，从原点指向机器人支撑轮的方向为速度正方向，右转为角速度正方向。然后将机器人驱动轮半径和两驱动轮距离代入公式(2)中计算出运动学模型，最后根据运动模型设计实验。

定位信息获取技术用来提供两轮驱动机器人的位置、姿态等信息，它是能否对机器人实现控制的基础[13-14]。为实现实验验证，本文选用视觉定位技术来获取机器人的位置信息。视觉定位技术是一种能够得到较为精准位置信息的定位技术，通过在环境中设置的摄像机来采集机器人的位置信息[15]。

图5 两轮驱动机器人实验平台Fig.5 Two-wheel-drive robot experimental platform

实验在Vicon实验室环境下完成，如图6所示。

图6 Vicon实验室Fig.6 Vicon Laboratory

Vicon即光学运动捕捉系统，是通过视觉的方式来采集实验环境中标记物的位置。在该实验环境中，上位机接收到摄像头提供的两轮驱动机器人位置信息，通过建模计算出两轮驱动机器人当前所处的位置坐标以及航向角度，最后通过计算得到两轮驱动机器人当前的速度，从而形成闭环反馈[16]。在得到机器人的基本信息后，由上位机通过蓝牙模块向机器人发送指令，进行路径跟踪实验。

3.2 实验结果及分析

首先为了验证双闭环控制方法的有效性，分别对直线路径和较复杂的曲线路径进行跟踪。在此基础上通过外力使两轮驱动机器人偏离期望路径后再进行路径跟踪，以验证矢量场法的有效性。最后通过模拟两轮驱动机器人的真实工作环境，先利用文献[17]中提出的局部路径规划算法进行路径规划，再对规划出的路径进行跟踪，验证本文提出的路径跟踪控制方法的实用性和有效性。由上位机采集实验过程中两轮驱动机器人的位置、速度以及航向等信息，为方便对比分析，采用Matlab对数据进行处理，并将实验时两轮驱动机器人运动轨迹绘制在二维平面上。

首先，进行了对于直线路径的跟踪，图7所示为引入控制算法前后两轮驱动机器人行走轨迹的对比图。直线路径比较简单，两轮驱动机器人只需保持恒定的速度大小和方向行驶即可。但从图中可以看出，由于无人小车的固有误差以及实验环境所存在的误差，在引入控制算法前，两轮驱动机器人并没有跟踪实验所期望的直线路径，而是沿着一条逐渐向左偏离的曲线行驶。在引入控制算法之后，控制算法对误差进行了有效的修正，两轮驱动机器人基本可以沿着一条直线行驶（如图中虚线所示）。

图7 引入控制算法前后轨迹对比图Fig.7 The trajectory contrast map before and after the introduction of the control algorithm

考虑到直线路径跟踪较为简单，设计了对较复杂的路径进行跟踪的实验。路径由以下函数表示：

该函数中t为变量，代表时间，函数图形为从原点出发，经过一个曲率随时间变化的曲线，最终回到原点。图8所示为实验结果，通过两轮驱动机器人轨迹可以看出，两轮驱动机器人成功完成了轨迹跟踪任务并最终回到原点，图中，轨迹X方向的范围为3.00 m，Y方向的范围为1.70 m，用矢量表示即为3.45 m。把图中每个实际跟踪点的误差矢量与轨迹范围矢量的比值定义为每个实际跟踪点的相对误差，求取各跟踪点的相对误差的均方差为0.86%，最大相对误差为3.64%。

图8 较复杂路径跟踪实验结果Fig.8 Experimental results of complex path tracking

本文所设计的两轮驱动机器人路径跟踪控制算法中引入了矢量场，即当两轮驱动机器人初始位置或在行驶过程中由于意外偏离期望路径时，两轮驱动机器人能够在矢量场的引导下快速回归期望路径。为验证矢量场法的有效性，在上述两个实验的基础上，通过外力将两轮驱动机器人的初始位置放置在偏离期望路径0.5 m左右的地方，期望路径为直线路径。图9为两轮驱动机器人偏离期望路径时的实验结果。

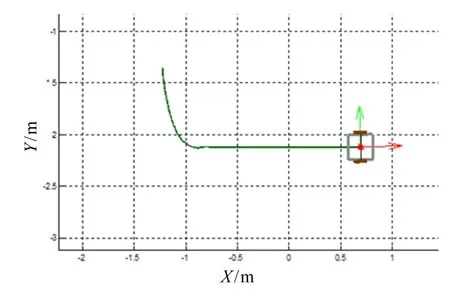
图9 两轮驱动机器人偏离期望路径时实验结果Fig.9 Experimental results of two-wheel-drive robot deviating from the expected path

通过两轮驱动机器人的轨迹可以看出，与传统的PID控制相比，当机器人的初始位置偏离期望路径时，本文设计的控制方法能够使机器人在矢量场的作用下，快速回归期望路径。并且，在回归过程中，前期回归速度较快，几乎沿着垂直于期望路径的轨迹行驶，当逐渐靠近期望路径的时候，机器人航向与期望路径之间的夹角逐渐变小，直至与期望轨迹重合，这种回归方式也更加符合工程的实际需求。

在实际应用中，两轮驱动机器人通常会预先根据环境信息进行路径规划，再对规划的路径进行跟踪，图10为避障路径跟踪实验结果。在路径上设置三个随机的障碍物，检测到障碍物后，采用局部路径规划算法计算出避障路径[15]，再由两轮驱动机器人对避障路径进行跟踪。通过实验结果可以看出，本文设计的两轮驱动机器人路径跟踪控制方法可以对避障路径进行跟踪，完成避障任务。

图10 避障路径跟踪实验结果Fig.10 Experimental results of obstacle avoidance path tracking

4 结 语

两轮驱动机器人的路径跟踪是其运动控制的基础。本文提出了一种两轮机器人路径跟踪控制方法，通过左右轮的双闭环PID控制来约束两轮驱动机器人的速度和位姿。在此基础上，在期望路径附近建立矢量场，引入位置约束，由此可以促使两轮驱动机器人在偏离期望路径时能够快速回归，完成路径跟踪任务，增强两轮驱动机器人的鲁棒性。在完成控制方法研究后，搭建了两轮驱动机器人硬件实验平台，设计了能够体现控制算法特点的实验方案，具体实现了两轮驱动机器人的路径跟踪控制，实验结果表明，被控两轮驱动机器人能够准确跟踪期望路径，由较复杂路径跟踪实验结果得出的各跟踪点的相对误差的均方差为 0.86%，最大相对误差为 3.64%。通过实验验证了提出的两轮驱动机器人路径跟踪控制方法的实用性和有效性。