基于CEEMDAN改进阈值滤波的微机电陀螺信号去噪模型

张 宁，刘友文

（1.闽江学院 物理学与电子信息工程学院，福州 350108；2.闽江学院 海洋学院，福州 350108）

微机电系统（Micro-Electro-Mechanical System，MEMS）陀螺具有成本低、重量轻、体积小等显著优点，在目前的低成本惯性导航系统中得到了非常广泛的应用。但MEMS陀螺与传统陀螺相比较，其精度要偏低，主要原因在于其输出的信号中含有较大的随机漂移误差[1]。考虑到MEMS陀螺的随机漂移具有非平稳性、弱非线性的特点，需要对其进行去噪处理。当前，对其进行去噪的常用方法有 Kalman滤波法和小波分析法。但 Kalman滤波法会存在由于误差模型建立不准确而导致出现滤波发散的现象[2]；小波分析法在 MEMS陀螺信号去噪中已经取得了较多的成功应用[3-5]，但该方法需提前设置小波基函数和分解级数，在滤波去噪过程中并不具有自适应性。

近年来，一种自适应信号处理方法——经验模态分解（Empirical Mode Decomposition, EMD）被广泛研究，并在MEMS陀螺信号去噪中得到了一定的应用[6-8]。但EMD方法本身存在有易产生模态混叠现象的缺点。为此，Wu通过添加辅助噪声，提出一种集成经验模态分解（Ensemble Empirical Mode Decomposition，EEMD）方法以消除模态混叠问题[9]；但EEMD方法也存在着在信号分解过程中没有完全消除白噪声、重构信号时误差较大的缺点。Yeh等人通过采用正、负成对的形式加入辅助噪声，提出了一种互补集成经验模态分解（Complementary EEMD, CEEMD）方法，以消去重构信号中的残余辅助噪声并降低模态混叠的影响。该方法在MEMS陀螺信号去噪中也得到了应用[11]。但CEEMD方法不能解决在添加不同噪声时可能分解出不同数量模态的问题。就此，Torres等人提出了完备集成经验模态分解（Complete Ensemble Empirical Mode Decomposition with Adaptive Noise, CEEMDAN）方法[12]，该方法通过附加自适应白噪声，不仅能减轻模态混叠现象，而且可以精确重构原始信号。

鉴于 CEEMDAN方法在信号自适应分解中的优势，本文考虑将其应用到MEMS陀螺信号去噪中来。目前使用EMD方法进行MEMS陀螺信号去噪时，主要采用两种方式：一是将其分解后的前几阶高频固有模态函数（Instrinsic mode function, IMF）分量认定为噪声分量，直接去除后进行信号重构，这属于强制去噪方法；二是对高频IMF噪声分量进行阈值处理，并进而与剩余有效IMF分量重构以获得去噪后信号。一般来说第二种去噪方式更加合理，因为高频噪声分量也可能包含有效成分，其阈值处理方式借鉴采用的是小波软、硬阈值函数。但采用硬阈值函数处理方式会使得重构信号产生振荡；而采用软阈值函数处理方式虽然信号连续性较好，但其影响了重构精度[4]。

本文中，为了对MEMS陀螺输出信号进行去噪，首先使用CEEMDAN方法对其进行有效完备的分解，并判断出噪声IMF分量与有效IMF分量间的界限；在此基础上，综合软、硬阈值函数的优缺点，提出了一种改进的阈值处理函数，并借鉴 EMD阈值设置的方法对分解后的含噪IMF分量进行阈值滤波处理；将阈值滤波处理后的分量与有效IMF分量进行信号重构即可获得去噪后信号。

1 CEEMDAN的基本原理

CEEMDAN方法是以EEMD方法为理论基础，通过对每一阶分解后的IMF分量添加自适应的白噪声信号，并计算唯一的残差信号以获取固有模态函数。其算法流程为：

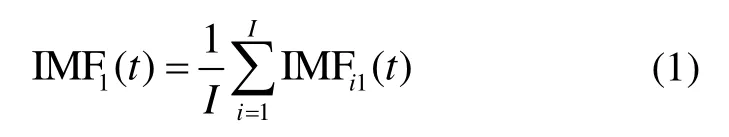
则第一个残余分量为：

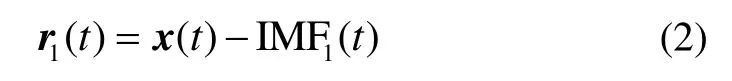
② 定义算子 Ej(·)为信号通过 EMD分解后得到的第j个模态函数。对信号继续进行I次重复分解，可得到第二个IMF分量为：

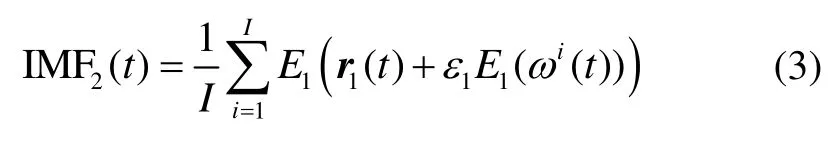
③ 对于 k = 2,…,K，计算k阶残余分量为：

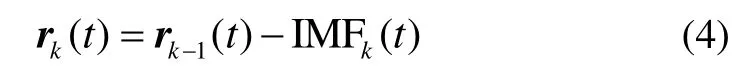
⑤ 重复执行步骤③和④，直到残余信号不可再继续被分解为止，最终可得到K个模态函数分量，其最终残差分量为：

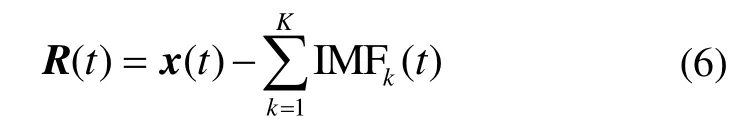
式(6)原始信号x(t)可以被表示为：

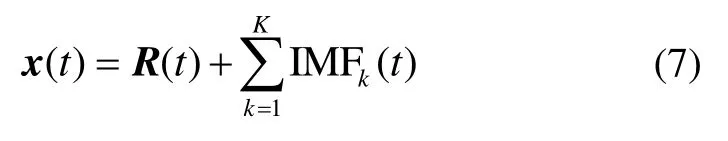
从上述 CEEMDAN方法的原理可以看出，CEEMDAN充分利用了EEMD噪声辅助分析的特点，可对原始信号进行精确完整的重构。并通过在每个阶段调整噪声系数εi可以选择不同信噪比的噪声。

2 CEEMDAN改进阈值滤波去噪模型

2.1 小波阈值函数分析

对分解后的IMF分量使用阈值去噪处理，常采用的是小波阈值函数，有两种形式：

① 硬阈值函数：

② 软阈值函数：

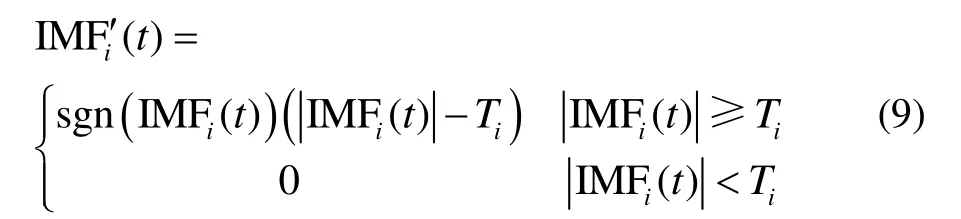
2.2 改进阈值函数

综合上述软、硬阈值函数的优缺点，并根据文献[13]半软阈值的思想，本文提出以下改进阈值函数，以适用于CEEMDAN分解后的IMF分量阈值处理：

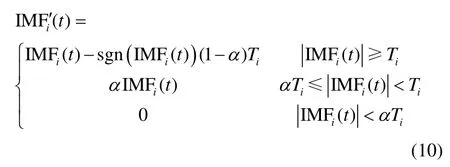
为此，本文所提改进阈值函数在对软、硬阈值进行线性组合的同时，又加入了这一项，充分考虑到在IMF分量较小时，能保留其中的有效成分。

图1给出了采用三种阈值函数对IMF分量处理后的结果对比示意图，其中IMF分量取值为 -1︰0 .01︰1，阈值Ti设置为0.3，α设置为0.4。

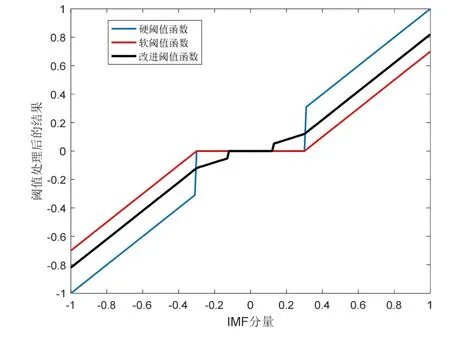
图1 三种阈值函数对比图Fig.1 Comparison on three threshold functions

从图1可以看出，改进的阈值函数不仅对硬阈值和软阈值进行了折衷处理，并在IMF分量取值较小时保留了其有效成分，而且具有较好的连续性。

2.3 基于CEEMDAN改进阈值函数的滤波去噪流程

在采用 CEEMDAN方法对陀螺输出信号进行有效分解的基础上，本文采用相关系数法[14-15]判断出噪声分量层数；进而对含噪IMF分量设置相应阈值，并对其使用改进阈值函数进行滤波去噪处理；最后将滤波后的含噪IMF分量与有效IMF分量进行重构以获得去噪后信号。其具体去噪流程如下：

① 对原始陀螺输出信号x(t)使用CEEMDAN进行分解，分解后得到K个固有模态函数分量IMF和一个残差分量R(t)；

② 计算各个IMF分量与x(t)的一系列相关系数，当相关系数首次出现局部极小值时，则判定该IMF分量为噪声分量与有效分量的界限，记其为第K1个IMF分量[14-15]；

③ 对前K1个IMF分量使用式(10)所示的改进阈值函数进行滤波处理。阈值确定的方法采用 EMD方法中的阈值计算模型[16]：

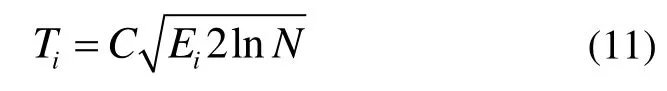
其中，C为一常数，在本文中取值为 0.3；N为信号长度； Ei为第i阶IMF对应的能量，其值可以使用下列公式进行估计。

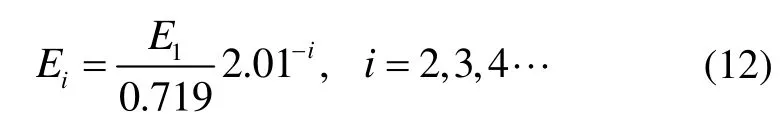
此处 E1为第一阶IMF对应的信号能量，采用如下公式进行计算：

④ 将阈值滤波后的含噪IMF分量与有效IMF分量进行重构，获得去噪后的信号为：

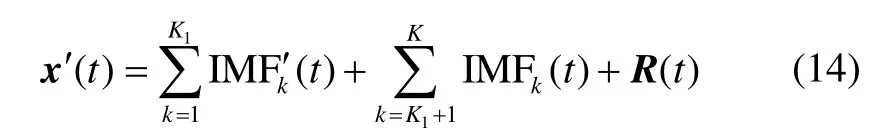
2.4 去噪效果评价指标

本文采用两种评价指标对陀螺信号的去噪效果进行评价：

① 信噪比：

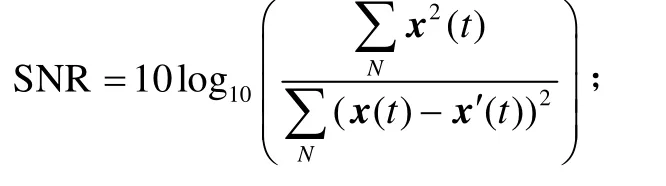
② 均方根误差：

3 实例分析

实验中采用MPU6050型MEMS惯组进行数据采集，该设备包括有三轴陀螺仪和三轴加速度计。本文以X轴陀螺仪数据为例，以100 Hz的采样频率采集了一组6 min的静态实验输出数据作为陀螺仪随机漂移时间序列，其数据长度为36 000，如图2所示。

图2 陀螺漂移实验数据Fig.2 Experimental data of gyro drift

使用CEEMDAN方法对实验数据进行分解，其中噪声标准差设为0.2，集成平均次数设为100[12]。经分解后可以得到15个IMF分量与1个残余分量。为了说明CEEMDAN方法在信号重构中的优越性，另外使用EMD、EEMD、CEEMD三种方法对实验数据进行了分解。对各种方法分解后的分量加以重构，与原实验数据对比以计算重构误差，结果如图3所示。四种信号分解方法的重构精度，如表1所示。

图3 四种方法的重构误差Fig.3 Reconstruction errors of three methods

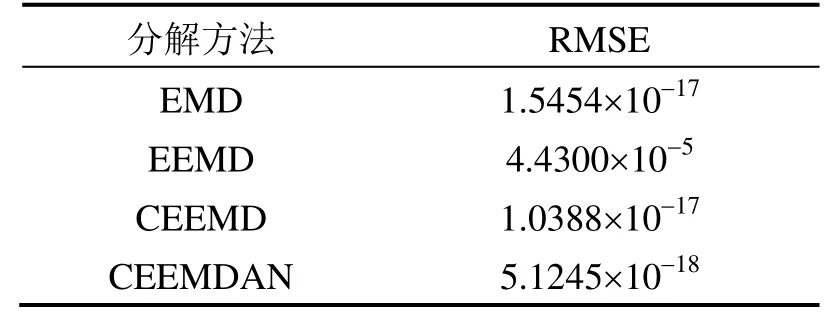
表1 信号重构误差精度Tab.1 Accuracy of signal reconstruction error

从图3可看出，EMD方法、CEEMD方法、CEEMDAN方法的重构误差数量级为 10-17，可以忽略不计，而EEMD方法的重构误差相对较大。从表1可以看出，CEEMDAN的重构精度最优，表明其具备了完备重构信号的性能，在信号分解中具有明显的优越性。

为了对实验数据进行去噪处理，计算分解后的所有IMF分量（包括残余分量）与原始实验数据间的相关系数，如图4所示。

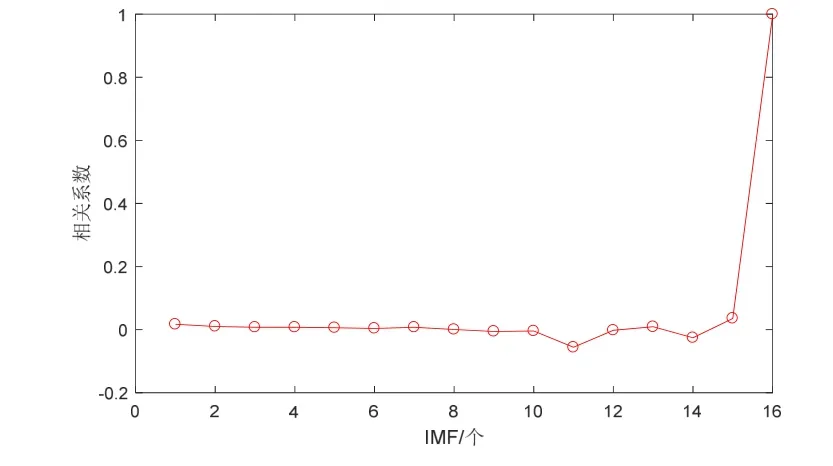
图4 各个IMF分量与原实验数据间的相关系数Fig.4 Correlation coefficient of each IMF and original experimental data

从图4中可以看出，在第11个IMF分量处首次明显出现局部极小值，所以判定前11个IMF分量为噪声分量。为了使用改进阈值函数对CEEMDAN分解后的含噪IMF分量进行滤波处理，需合理给定式(10)中α的取值。为此，对α从0开始按照步长为0.05循环计算使用改进阈值去噪后的信噪比，绘制曲线如图5所示。可以看出，α取值为0.5时信噪比最佳。

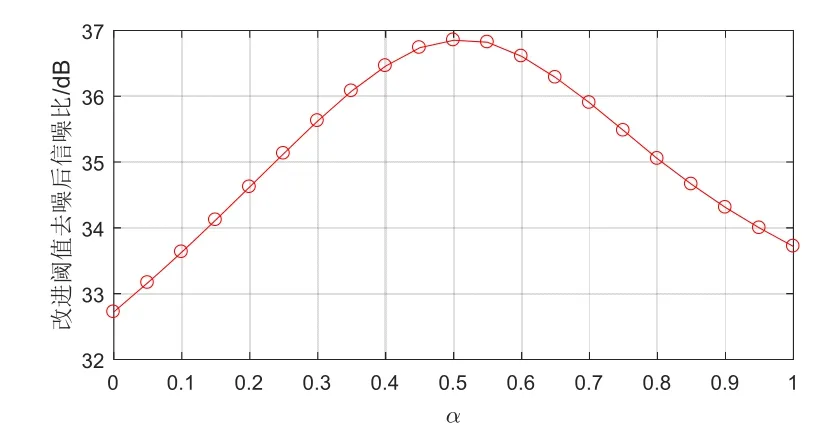
图5 改进阈值函数参数与去噪后信噪比的关系Fig.5 Relationship between improved threshold function parameter and SNR after de-noising

为了与本文方法的去噪效果进行对比，本文还对实验数据分别使用了小波分析、EMD、EEMD、CEEMDAN和CEEMD阈值滤波方法进行去噪处理。其中EMD、EEMD、CEEMDAN使用的是强制去噪处理，即使用相关系数法在判断出噪声层数后，直接舍去噪声分量进行重构以获得去噪后信号；小波分析法使用的是软阈值处理方式，设置的小波基函数和分解级数分别为sym 3和7；CEEMD阈值滤波方法采用文献[11]所示方法，其中随机噪声参数H设置为0.7。去噪后的评价指标对比如表2所示。

从表2中可以看出，本文所提出的CEEMDAN改进阈值滤波方法在去噪后其信噪比明显最大，同时其均方根误差明显最小，表明该去噪方法最优；而在强制去噪方法中，CEEMDAN方法也要优于EEMD和EMD方法，表明了其具有更好的信噪分离效果；CEEMD阈值滤波方法的去噪效果也要明显劣于本文方法；而在本文的小波参数设置下，小波分析法去噪效果最差。本文方法相对于其余五种去噪方法，其信噪比普遍提高了至少约3.9 dB，均方根误差普遍降低了至少约36%。

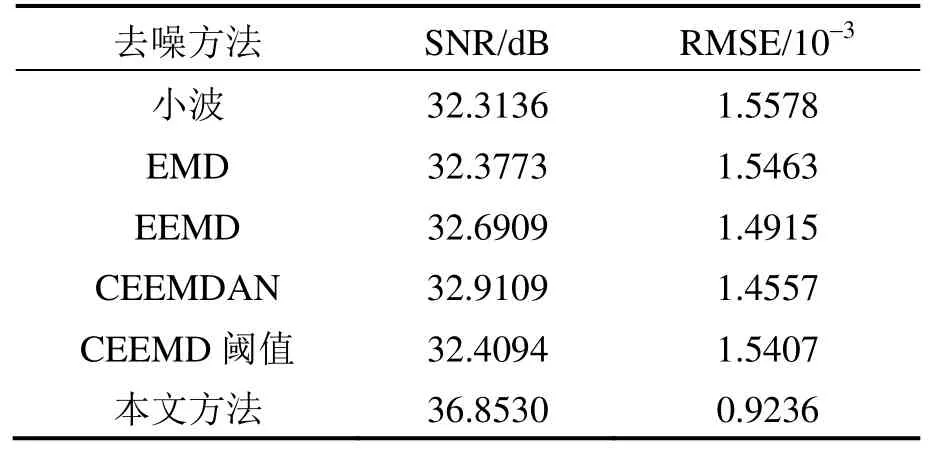
表2 各种方法的去噪评价指标对比Tab.2 Comparison of de-noising evaluation indexes of various methods

为了对比软、硬阈值函数与本文所提改进阈值函数去噪的性能，本文还给出了CEEMDAN分解后，使用三种阈值函数进行去噪的指标，如表3所示。

表3 三种阈值函数的去噪评价指标对比Tab.3 Comparison of de-noising evaluation indexes of three threshold functions

从表3可以看出，采用本文所提出的改进阈值滤波去噪的效果要明显优于软阈值和硬阈值的去噪效果，其信噪比分别提升了4.1335 dB、3.1347 dB，均方根误差分别降低了37.9%、30.3%；对比软、硬阈值的去噪效果，硬阈值稍优。采用CEEMDAN结合软、硬、改进阈值去噪的结果如图6～8所示。

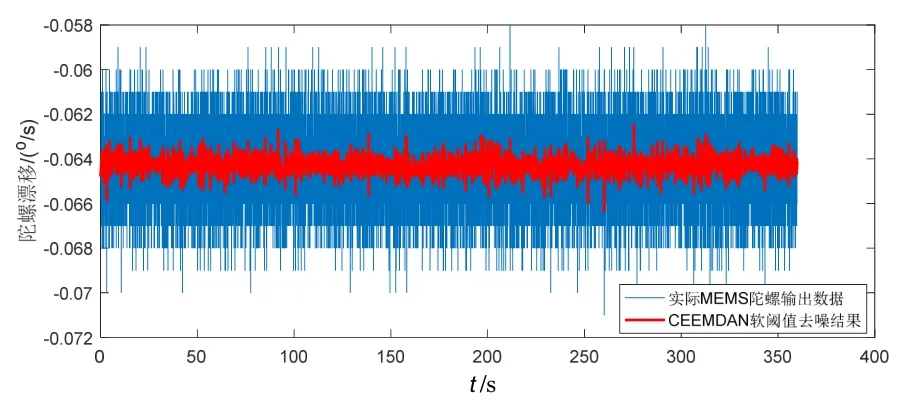
图6 CEEMDAN软阈值去噪结果Fig.6 CEEMDAN soft threshold de-noising result

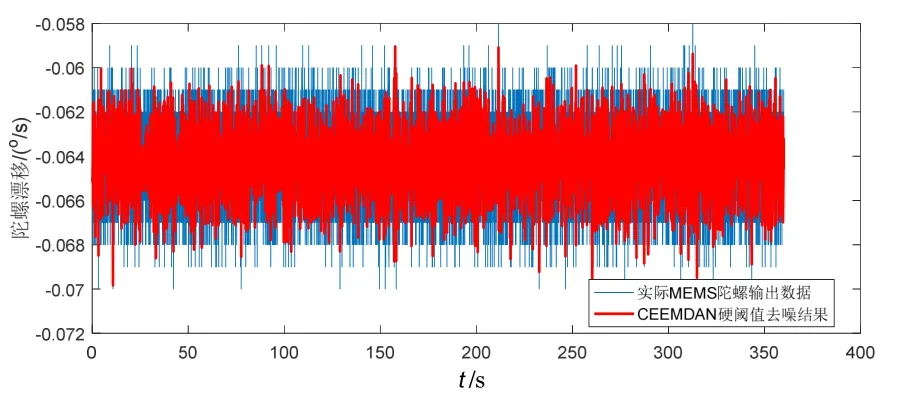
图7 CEEMDAN硬阈值去噪结果Fig.7 CEEMDAN hard threshold de-noising result

图8 CEEMDAN改进阈值去噪结果Fig.8 CEEMDAN improved threshold de-noising result

对比图6、图7、图8可以看出，本文所提方法的去噪图形在硬阈值和软阈值去噪图形间得到了明显的折衷。另外由于改进阈值函数中考虑了微小有效成分的贡献，使得所提方法的去噪性能得到显著改善，充分表明了本文所提方法的有效性。

4 结 论

本文在考虑到 CEEMDAN方法能够对信号进行有效完备分解的基础上，提出了一种基于改进阈值函数的 CEEMDAN滤波去噪模型。该模型通过借鉴EMD阈值设置方法，对CEEMDAN分解后的含噪IMF分量使用改进阈值函数进行滤波处理，并进而对处理后的含噪分量与有效分量进行重构以得到去噪后的信号。通过对实际MEMS陀螺输出信号进行详细的去噪分析，结果表明本文所提模型在去噪性能上要明显优于CEEMDAN、EEMD、EMD强制去噪方法、CEEMD阈值滤波方法和小波分析方法。另外使用改进阈值函数后的去噪性能要显著优于软、硬阈值函数处理后的去噪性能。这也充分验证了本文所提模型应用于MEMS陀螺信号去噪中具有的可行性和优越性。