几种GNSS接收机跟踪环路配置的对比分析

汤新华，陈 新，修金城，陈熙源

（1.东南大学 仪器科学与工程学院，南京 210096；2.上海交通大学 上海 200000；3.微惯性仪表与先进导航技术教育部重点实验室，南京 210096；4.济南市勘察测绘研究院，济南 250000）

随着定位服务应用范围的拓广和精度要求的日益提高，全球卫星导航技术的重要性日益彰显。特别在国内北斗卫星导航系统日益完善趋势中，对应的接收机技术也在不断改进，一方面是针对卫星系统本身的改变（如新型信号调制方式，多卫星系统等），对接收机结构进行相应调整；另一方面主要是针对信号传播环境因素（如多路径，弱信号等），进一步改进基带的信号处理技术。在传统接收机中，卫星信号的处理过程，可以简单分为：信号的捕获、跟踪和位置速度时间（PVT）解算三个阶段。其中，标量跟踪环路一直被惯用至今，它的设计更多的注重单维的参数估测控制（比如载波频率控制环路（FLL），载波相位控制环路（PLL），码相位控制环路（DLL）等），其中FLL、PLL、DLL都共享了一个控制环路设计方案[1]。在实际应用平台中，一般从动态性能和精度方面开展研究。为了进一步提高系统的动态性能，并且加速信号锁定、避免假锁等，S.Alban[2]、唐康华[3]等国内外学者提出了典型的FLL-PLL/DLL[4]或基于外界辅助的跟踪环路设计[5]等组合环路方案；为了进一步提高伪距和对应的定位精度，Letizia Lo Presti[6]等提出了载波平滑技术，但是该方法需要保持载波相位计算的连续性与平滑时间常数M大小的相位数据信息。

随着 Kalman滤波的引入，从信息融合技术的角度出发，为了提高跟踪环路中各个参数的估测精度，各种数据融合技术被不断地尝试用到跟踪环路当中。其中，基于 Kalman的跟踪环路设计研究方案已成为一个热门的典型新型设计方案。跟传统跟踪环路相比，基于 Kalman的跟踪环路将所需估测的参数（多普勒频移，码相位，载波相位等）通过Kalman（系统方程和观测方程）进一步的融合，以达到可用信息的最大化利用，这是基于 Kalman跟踪环路能在精度和动态性能具有更好表现力的重要因素[7-9]。

本文主要分析Kalman跟踪环路与传统跟踪环路、载波相位平滑伪距技术之间的内在关联，从理论及实验证明以上各个算法数据融合实质的一致性及等效性。

1 跟踪环路简介

GNSS接收机基带信号处理主要包括捕获、跟踪、PVT解算三个部分，其中跟踪环路是核心部分，主要负责卫星信号（ y[n]）中的多普勒频移（ fd）、载波相位（φ0）、码相位延迟（τ）的持续估测。

其中，A为信号幅值，fIF为信号中频频率，fd为多普勒频率，φ0为载波初始相位，Ts为采样周期，n为时间离散序列编号，c(nTs-τ)为PRN伪随机码，sb(nTs-τ)为副载波（若无副载波调制，等于1），d(nTs-τ)为导航电文，cos[2π(fIF+fd)nTs+φ0]为载波，η[n]为噪声。

1.1 传统跟踪环路设计

传统跟踪环路包括载波频率控制环路（FLL），载波相位控制环路（PLL），码相位控制环路（DLL），分别用于df、φ0、τ的正确估测。

如图1所示，传统FLLDLLPLL环路都是基于最小均方差根误差为目标设计的经典控制模型[1]，一般采用2阶或3阶系统。其中，输入输出的求差操作由鉴相器鉴频器完成，由于鉴相器鉴频器的牵引范围（pull-in）及非线性特性限制了该模型的适用范围，从而需考虑跟踪环路的假锁现象、鉴相器鉴频器对输入信号中白噪声的属性改变、各跟踪环路经验跟踪门限值（Rule-of-Thumb Threshold）计算[10]等。特别在参数配置过程中，更多地从控制系统属性（带宽及阻尼比）出发，这导致跟踪环路在信号参数估测中更多地体现出滤波控制功能，所以，一般在跟踪环路后续需要引入平滑技术（如 Carrier-Smoothing，PVT解算中的Kalman）来提高定位、定速精度。

图1 传统跟踪环路（FLLDLLPLL）控制模型Fig.1 Traditional tracking loop (FLLDLLPLL) model

1.2 载波平滑伪距技术

在传统跟踪环路跟踪基础上，为了进一步提高伪距精度（伪距很大程度上取决于码相位延迟（τ）的估测精度），充分利用卫星信号里面的载波相位信息，文献[5]提出了基于载波相位平滑（Carrier-Smoothing）技术的伪距平滑方法，其示意图如图2所示。

图2 Carrier-Smoothing伪距平滑技术Fig.2 Carrier-Smoothing algorithm structure

式中，rc[n]为基于码测量的伪距，rp[n]为基于相位测量的伪距，cs[n]为卫星种差引起的误差，cR[n]为接收机端种差引起的误差，T[n]为对流层引起的误差，I[n]为电离层引起的误差, N[n]为整周模糊度，λ为载波波长，wc[n]为DLL环路码相位估测噪声误差（一般考虑热噪声），wp[n]为PLL环路载波相位估测噪声误差。利用式(2)中的码伪距rc[n]与相位伪距rp[n]的关联可以推算出平滑伪距rsm[n]：

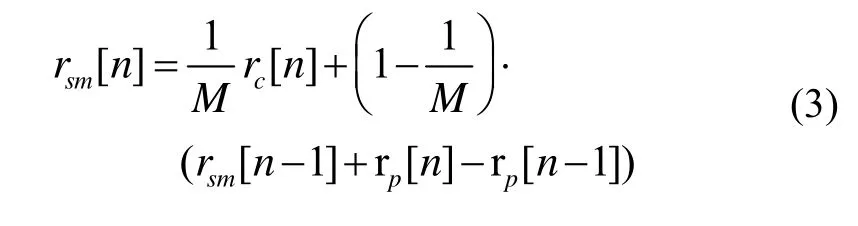
1.3 Kalman 跟踪环路

Kalman跟踪环路设计思路主要源于Kalman系统本身，如式(4)中，该方法利用系统方程将码相位误差Δτ、载波相位误差Δθ，载波频率误差Δf，载波频率变化率误差Δα关联，并同时用观测方程将载波鉴相器，码鉴相器输出与上述状态参数关联。

图3 基于KF的跟踪环路Fig.3 KF-based tracking loop

式(4)中，T为跟踪环路周期，β系数为单位cycle转为单位chip的比例系数（在GPS L1下β= 11540），wk′为系统状态量的离散误差矩阵，为码相位误差观测量，为载波相位误差观测量，vk′为观测状态量的离散误差矩阵。

基于分析EKF跟踪环路设计[11-12]、KF跟踪环路与传统跟踪环路对比理论分析[7]、KF跟踪环路的对应等效传统跟踪结构推导设计[8]等工作，Kalman跟踪环路优势可以总结如下：

① 可以将传统FLLDLLPLL所需估测对象通过系统方程进行耦合估测，这样可以提高估测值的精度。

② 通过系统误差方差矩阵 Q和观测方程误差矩阵R能很好地权衡各个变量之间的精度与动态效应。

从理论上进一步分析，式(4)中对应的Kalman跟踪系统可以近似等效于如图(4)跟踪结构。

图4 Kalman跟踪环路的近似等效模型Fig.4 Approximation model of KF-based tracking loop

由图4可知，Kalman跟踪环路的等效模型可以和传统跟踪环路相似，优势在于环路增益0K～3K，传统环路增益更多地从控制理论角度设计，而基于最小二乘法核心思路能完成自适应的 K0～K3。增益K0～K3与系统误差方差Q和观测误差方差R的关系如式(5)所示。相关的理论分析及证明参考我们先前的工作[8]。

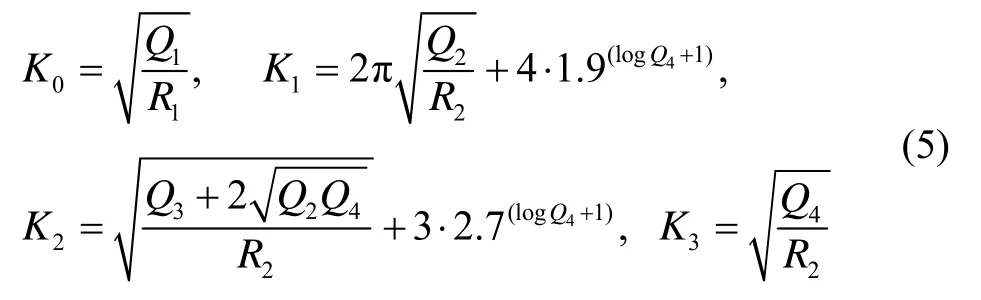
其中，Q1、 Q2、Q3、 Q4对应式(4)中状态量的误差协方差，R1、 R2对应式(4)中观测量的误差协方差。式(5)为Kalman的参数设置提供了极大的理论依据，可以从接收机动态性能要求，时钟精度等方面直接得出具体参数配置[8]。Kalman跟踪环路相比于传统跟踪环路最核心优势在于能提供精准的多普勒频移（ fd）、载波相位（φ0）、码相位延迟（τ）估测，这样可以简化后续相关模块，如 PVT解算模块、伪距差分（RTD）模块中的伪距精度及可靠性、相位伪距差分（RTK）模块中的相位信息精度及可靠性等。

2 接收机基带信号处理的不同结构对比分析

为了验证 Kalman跟踪环路的优越性及与传统跟踪环路的可等效性，下面主要从定位、定速精度出发分析不同基带信号处理结构的实验结果。

如图5所示，本文中提出4种结构方案，在跟踪环节有两种方案，分别为传统跟踪环路和Kalman跟踪环路，在定位引擎中有基于 Kalman的 PVT解算模块（KF-PVT）与基于最小二乘法的PVT解算模块（LSPVT），在两环节中间存在可选择的载波平滑伪距模块（CS）配置，由第1节的简介可知，跟踪模块主要提供多普勒频率、载波相位、码相位、导航电文信息，CS模块主要对伪距进行平滑处理。最后KF-PVT的精度一般高于LS-PVT，但是计算复杂度也较高。为了验证 Kalman跟踪环路的优越性及与传统方案的可等效性，本文采取了4种方案从定位、定速精度角度进行了对比及等效分析。方案配置总结如下：

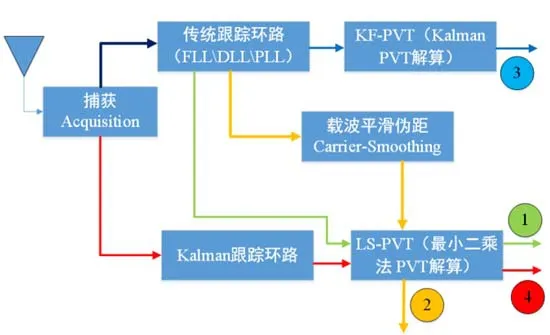
图5 四种对比方案结构Fig.5 Proposed four different receiver structures

方案1：传统跟踪环路(FLL/DLL/PLL)+LS-PVT。

方案2：传统跟踪环路(FLL/DLL/PLL)+载波平滑+LS-PVT。

方案3：传统跟踪环路(FLL/DLL/PLL)+KF-PVT。

方案4：卡尔曼跟踪环路+LS-PVT。

在方案配置设计选择中，主要为了区分不同跟踪环路的跟踪精度，跟踪精度体现在对多普勒（对应 PVT速度）、码相位（对应伪距）、载波相位等观测量的估测。其中，在传统跟踪环路设计中主要采用了FLL辅助的二阶PLL环路及一阶DLL环路，环路参数由传统基于环路带宽及阻尼比经验公式获得。在Kalman跟踪环路设计中，采用了式(4)描述系统。

3 不同配置方案的实验分析

图6 实验定位轨迹（由Septentrio接收机提供参考基准）Fig.6 Reference trajectory

在实验中，主要通过数据前端设备实时采集数据。数据由意大利ISMB实验室NavSAS组提供，采集地点德国，持续时间7 min左右。同时，在试验中采用Septentrio PolaRx3eTR GPS接收机结果作为基准，该接收机配置在 SBAS增强模式，精度为水平0.6 m、高度0.8 m。

3.1 定位结果对比分析

在试验中采用Septentrio PolaRx3eTR GPS接收机结果作为基准，对图5所示的4种方案进行了对比。结果如图7所示，在实验400 s期间内，各个方案的定位误差平均和方差结果如表1所示。

图7 各种方案定位轨迹结果及定位误差（以Septentrio为参考）Fig.7 Trajectories and positioning errors of the four solutions

表1 定位误差统计Tab.1 Positioning errors statistics

由表1数据表明，方案4是最佳方案，其中方案 2与方案 4接近，从这个角度可以看出，Kalman跟踪环路在码相位估测上的精度与传统载波相位平滑伪距相当。另外，方案3的效果比方案1优势明显，但却不如方案 2、4，其中的主要原因在于 PVT计算引擎里面的 Kalman经验式参数设置方法的局限性所致。从侧面也说明先前工作[7]提出的Kalman跟踪环路配置方法优于目前KF-PVT中的Kalman配置方法。

3.2 定速结果对比分析

在定速结果比较分析中，主要考虑了各个接收机方案在地心坐标系（ECEF）坐标系下的X、Y轴方向的速度误差，如图8所示。

图8 各种方案ECEF坐标X/Y轴定速结果（以Septentrio为参考）Fig.8 Velocity estimate results of X/Y direction

如图9所示，以Septentrio接收机结果作为参考基准，得出各种方案的速度估测值。

图9所示结果的速度误差平均值与方差见表2。由表2可知，方案2虽然在定位精度上可以与方案4相当，但是在定速上较差，与方案1精度一致，这说明方案4在码相位及多普勒频率上都能得到精确的估测值。

表2 定速误差统计Tab.2 Velocity errors statistics

方案3 0.11 0.39 0.01 0.06方案4 0.02 0.14 -0.01 0.05

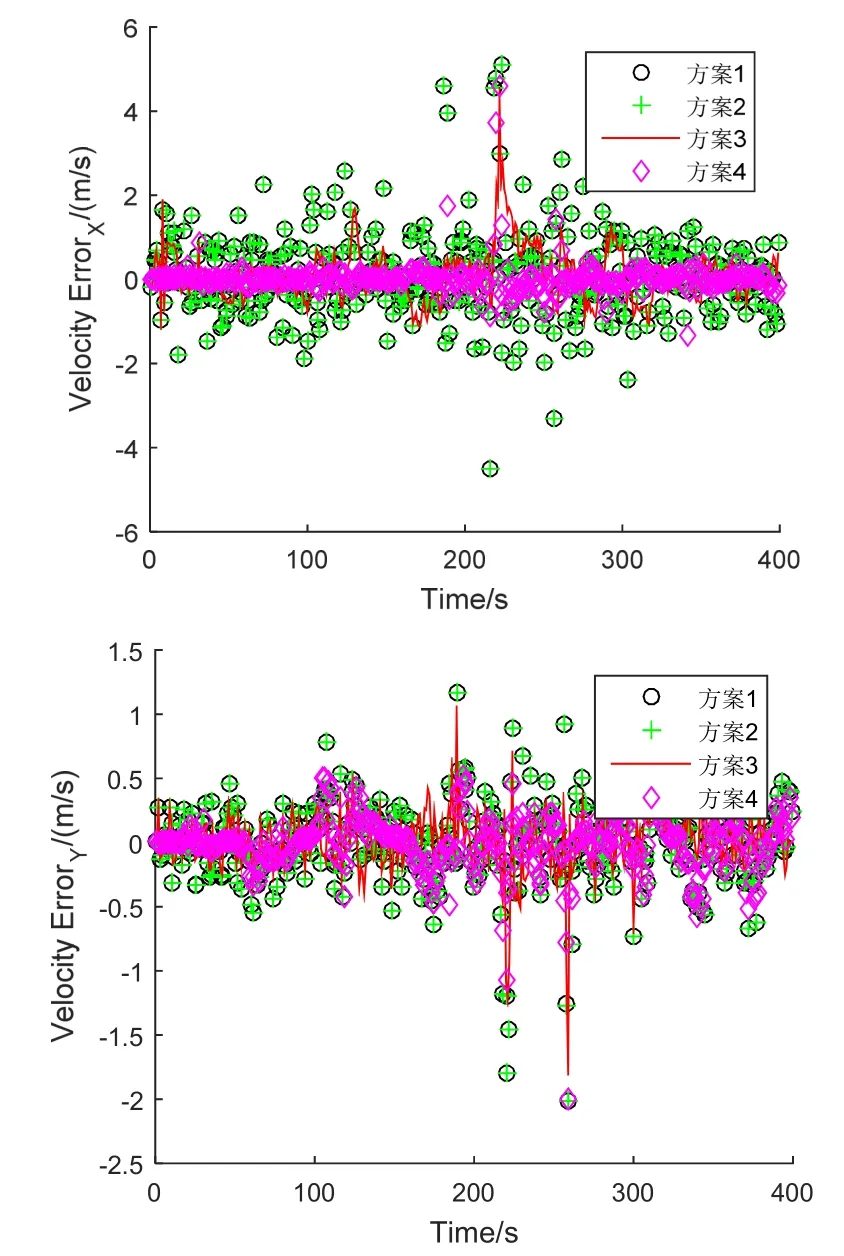
图9 各个方案X/Y轴定速误差（以Septentrio为参考）Fig.9 Velocity estimate errors of four solutions

4 结 论

本论文通过接收机基带架构方案的配置及对应的实验结果分析，得出如下结论：

① 式(4)中的 Kalman跟踪环路较传统配置的二阶跟踪环路体现出更好的参数估测精确度。但是，由图4可知，Kalman跟踪环路和传统跟踪环路是有等效性的，更多体现在环路阶数及参数设置不同。

② 方案4与传统接收机方案3对比，可以理解为Kalman滤波器的前置，由原先的PVT引擎模块移至跟踪环路，从PVT角度分析，效果相近（取决于PVT中Kalman滤波器参数正确配置）。但是，Kalman滤波器的前置直接获得了更好的跟踪环路参数估测。

从而可以得出 Kalman跟踪环路在跟踪环节就能提供高精度的码相位、多普勒频率、载波相位信息。一方面，后续的PVT引擎模块可以用结构复杂度较低的LST-PVT。另一方面，跟踪环节的参数精准估测对其他应用，如RTK，遥感接收机等提供很重要的观测基础。