基于统一横向坐标系的极区地球椭球模型导航方法
2018-12-20卞鸿巍林秀秀王荣颖
卞鸿巍,林秀秀,王荣颖,马 恒
(海军工程大学 电气工程学院,湖北 410033)
随着极区冰雪消融速度加快,极区战略地位提高,极区导航成为国内导航领域研究热点,与传统中低纬度导航不同,极区导航主要面临传统时空基准定义失效、墨卡托海图投影不再适用、惯导装备高纬度指向能力下降以及计算溢出等一系列问题[1]。极区导航坐标系是解决极区导航的基础。1995年,文献[2]提出横向坐标系解决了极点处惯导解算计算奇异的问题。文献[3-4]沿用横向坐标系的概念并在不考虑地理坐标系的情况下完成捷联惯导在横向坐标系下的导航编排方案。文献[5-6]等在地球模型为椭球模型情况下设计并提出了将横向地理坐标系作为导航参考坐标系的惯性导航力学编排。但是横向坐标系的提出主要针对极区惯导解算领域。针对极区航海需求,文献[7]提出格网坐标系以解决经线收敛造成传统航向参考线极区不可用问题。在实际极区应用中,惯导基于横向坐标系的解算得到的极区导航参数还需要同其他航海导航用户设备进行统一与转换。随着极区坐标系研究的深入,出现了多种不同横向坐标系和格网坐标系的定义形式,如文献[8-9]。不同投影方式的海图及格网航向基准也有多种格网坐标系的定义方式,如格林尼治格网坐标系、图幅中央经线格网坐标系、沿大圆航线格网坐标系等。极区坐标系产生和应用领域、定义方式和命名方式不统一增加了极区导航参数转换的复杂性,不同坐标系在不同领域的应用,导致导航系统间信息交联困难。
针对上述问题,本文定义了一种新的统一极区坐标系,该坐标系在极区实现了横向地理坐标系和格林尼治格网坐标系的统一,并将其统称为统一横向坐标系。在此基础上,推算出基于CGCS2000地球椭球模型的捷联惯导统一横向坐标系导航算法,解决了基于统一横向坐标系的椭球模型横向经纬线不正交的问题,以满足惯导新统一横向坐标系的使用需求,文章最后对上述理论和算法性能进行了仿真验证。
1 基于椭球模型统一横向坐标系定义
由于地球球体近似模型存在几何误差,难以满足高精度长航时导航的需求,需要对高精度导航使用的椭球体近似模型进行设计[6,10]。
统一横向坐标系的定义包含横向地球坐标系和横向地理坐标系的定义两部分。如图1所示,与其他文献[3-6]定义不同,横向地球坐标系Oxeyeze由传统地球坐标系Oxeyeze绕Oye轴仅需旋转−90°可得。根据横向地球坐标系定义可得到横向经纬网,即横向北极点为赤道和 180°经线的交点,横向赤道则由 90°W 和 90°E经线构成,横向本初子午线由180°经线北半球部分和0°经线构成。椭球面上任意一点的横向纬度φ为地球椭球外法线与横向赤道平面的夹角,椭球面上任意一点的横向经度为过该点的外法线矢量在横向赤道平面上的投影与Oxe轴矢量的夹角,传统等纬度圈为圆,但等横向纬度圈为不规则曲线,在示意图中不易表示,故定义一个平行于横向赤道面的平面切割地球形成的椭圆为等横向辅助纬度圈,图1中给出的横向纬度圈为横向辅助纬度圈,其上的点的横向纬度并不相等。
根据定义,等横向经线圈的切线矢量 T1、等横向纬线圈的切线矢量 T2以及等横向辅助纬线圈的切线矢量 T3如式(1)所示,并根据切线矢量推导出其关系式,如式(2)所示。

其中,a为地球椭球体长半径,e为地球椭球体第一偏心率。

图1 横向地球坐标系和横向地理坐标系Fig.1 Transverse earth coordinate system and transverse geographical coordinate system
由此可以看出横向经线与横向纬线、横向经线与横向辅助纬线均不正交。在惯导解算中横向纬线主要为横向东提供基准,故在惯导解算中仍使用横向纬度。横向地理坐标系定义如下:轴与横向经度圈相切,指向为横向北,轴为当地垂线,指向为天向,轴由右手定则确定,指向为横向东。定义横向北与航向线的夹角为横向航向。定义航速在横向东向上的分量为横东向速度,在横向北向上的分量为横北向速度。
根据以上统一横向坐标系的定义,通过几何关系,可以得到横向经纬度与横向地球坐标系的变换关系式如下:
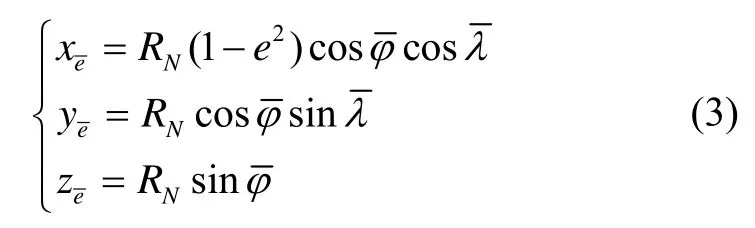

又因为,根据横向地球坐标系定义过程,可得到横向地球坐标系与地球坐标系的关系为式:

结合式(3)~(5)可推导出横向经纬度与地理经纬度的转换关系:
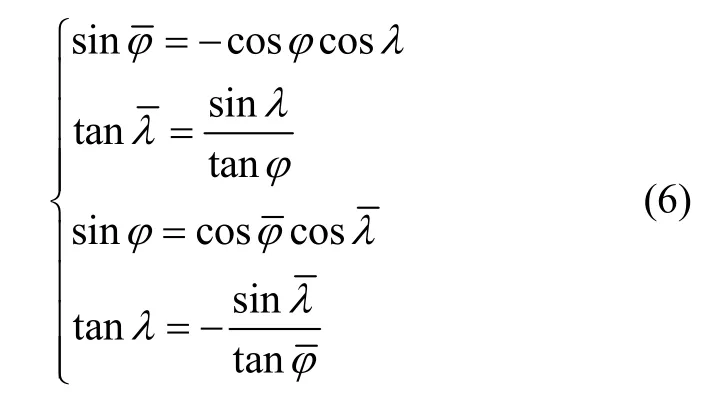
本文给出的与横向坐标系统一的格网坐标系本质上是一种地理坐标系,其与极区横向墨卡托海图格林尼治格网坐标系在极区范围内近似一致。其北向定义为平行于格林尼治子午面的格网平面与当地水平面的交线[11-12]。由统一横向坐标系定义可知,横向地理坐标系北向相切于横向子午圈,且北极地区在统一横向坐标系的横向赤道与横向本初子午线相交的区域。在极区范围内,横向子午圈的切线近似平行,由此定义的格网北与横向北已完全一致,两个坐标系天向一致。故在极区,横向地理坐标系与定义的格林尼治格网坐标系实现统一。在此基础上,再结合统一横向坐标系的惯导编排即可为解决北极地区定位和定向上的问题提供理论基础。
2 基于椭球模型的统一横向坐标系惯导编排
2.1 坐标系旋转特性
在基于捷联惯导的编排中,需要分别给出横向姿态解算、横向速度解算以及位置解算微分方程,故在推导编排前,先根据统一横向坐标系的定义过程,写出坐标系旋转特性。包括:从地球坐标系旋转到横向地球坐标系的姿态矩阵、从地球坐标系旋转到横向地理坐标系的姿态矩阵以及从载体坐标系旋转到横向地理坐标系的姿态矩阵[13]。
从横向地球坐标系的定义中,可以看出,从地球坐标系旋转到横向地球坐标系仅需要进行一次旋转操作,旋转过程可以表示为:

进一步可以写出从地球坐标系旋转到横向地球坐标系的姿态矩阵为:
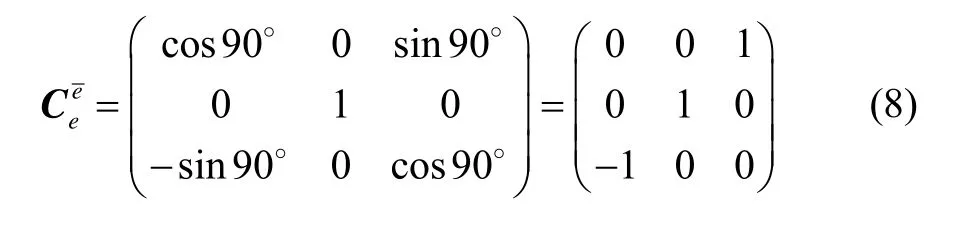
同理于地球坐标系旋转到地理坐标系的姿态矩阵,可得横向地球坐标系旋转到横向地理坐标系姿态矩阵为:

结合式(8)和式(9)可得从地球坐标系旋转到横向地理坐标系的姿态矩阵为:
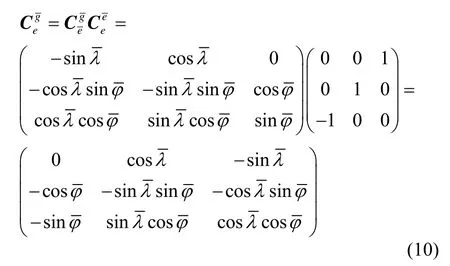
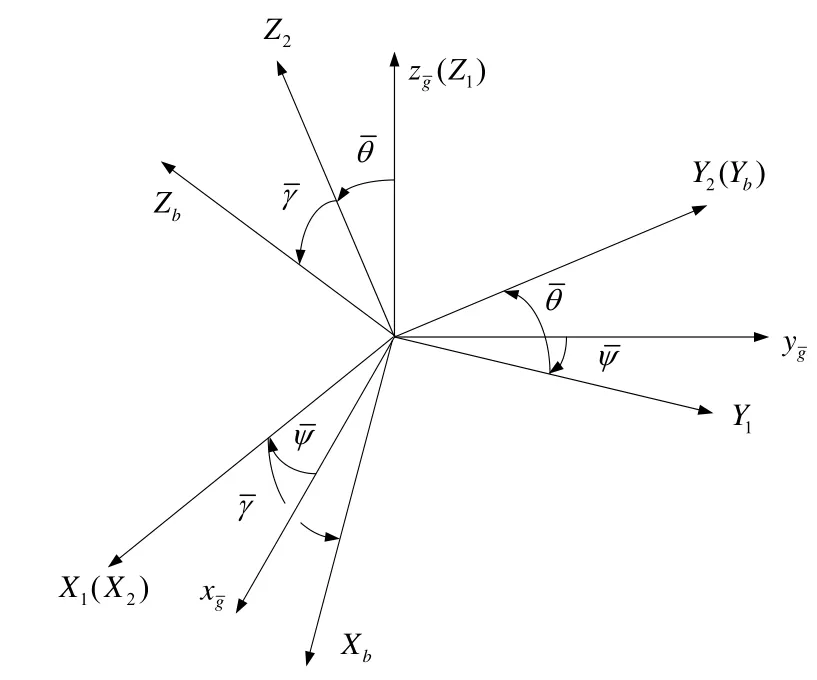
图2 横向地理坐标系与载体坐标系的旋转关系Fig.2 Rotation relationship between transverse geographical coordinate system and carrier coordinate system
横向地理坐标系可以经过三次姿态角的旋转得到载体坐标系,图2给出了横向地理坐标系与载体坐标系的旋转关系,载体的横航向角为,横纵摇角为,横横摇角为。即:


由坐标系X1-Y1-Z1绕X1轴旋转的姿态矩阵为:

由坐标系X2-Y2-Z2绕 Y2轴旋转γ的姿态矩阵为:
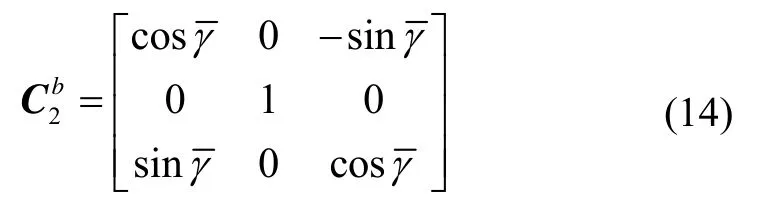
综上,结合式(12)~(14)可得载体坐标系旋转到横向地理坐标系的姿态矩阵为:
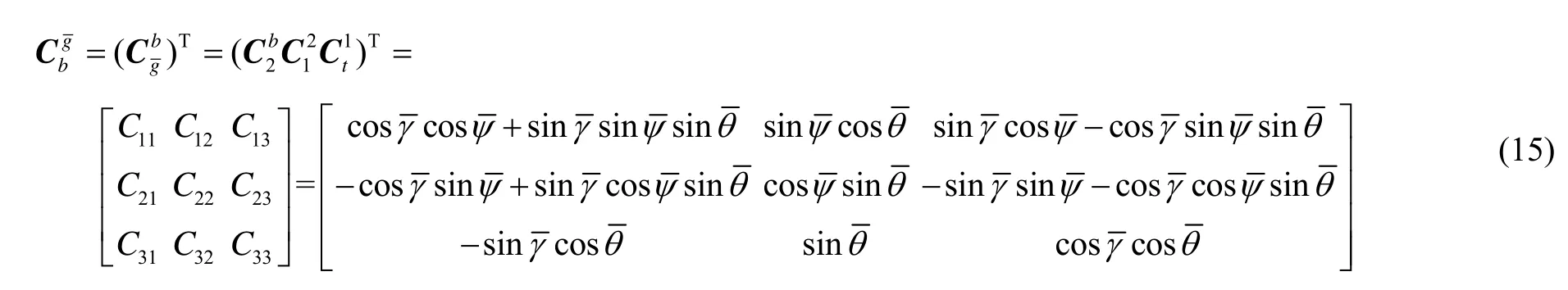
在推导出坐标系旋转特性的基础上,可以进一步推导基于椭球模型统一横向坐标系的惯导编排。由于基于椭球模型统一横向坐标系按照传统经纬线定义方法定义的横向经纬线不再互相正交,致使基于横向经纬线的惯导编排复杂性增加,为解决这个问题提出以下基于椭球模型惯导编排。
2.2 位置微分方程
载体运动会引起位置的变化,载体的运动速度可以分解为东向和北向两个方向速度,在统一横向坐标系中,载体速度分解为横东向速度和横北向速度。

结合式(3)和式(9)可求得:

其中,

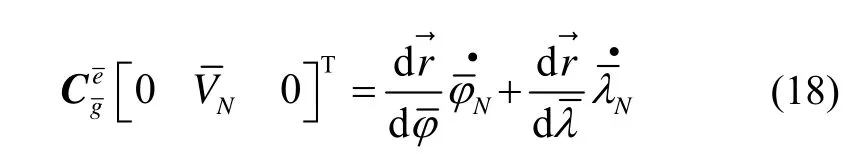
结合式(3)和式(9)可求得:
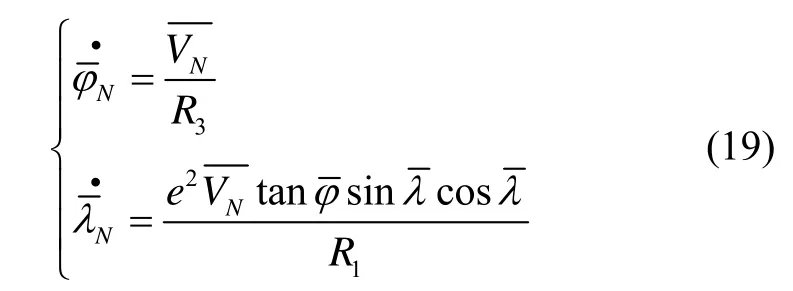
其中,
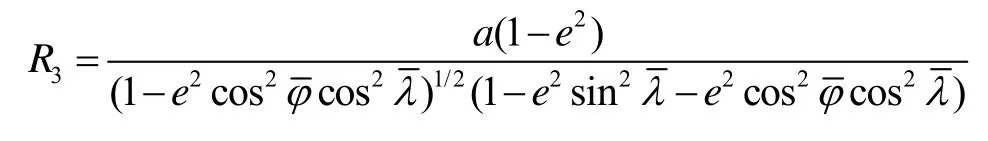
综合式(15)(17)可得载体运动引起位置变化为:
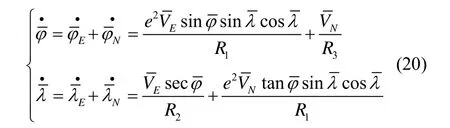
2.3 速度微分方程

同理,可以得到横向纬度变化率 在e系下的投影的单位矢量为q,且存在:

横向地理坐标系相对于地球坐标系的旋转角速度在地球坐标系上的投影与横向经纬度变化率及其在e系下的单位矢量相关,其具体关系如下所示:
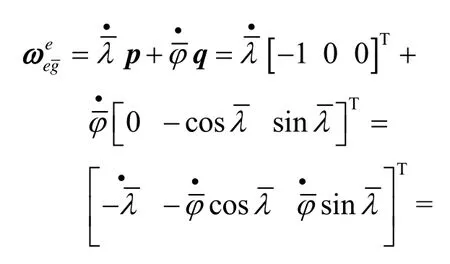

由前面推导的各个参数可以进一步给出速度微分方程的表达形式:

其中,
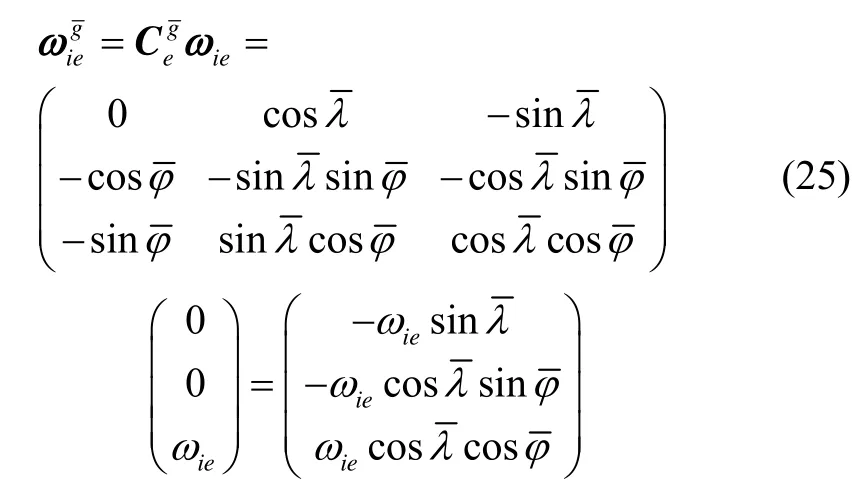
2.4 姿态微分方程
统一横向坐标系中姿态的更新由姿态微分方程确定:

3 仿真分析
由于实际极区试验开展困难,为验证基于统一横向坐标系的极区地球椭球模型导航方法的正确性和可行性。本文首先基于60°N附近中高纬度海域实船搭载的激光惯导的IMU实测数据,对比传统地理坐标系编排解算结果与本文提出的统一横向坐标系编排解算结果,验证编排的正确性。然后在极区对统一横向坐标系编排进行仿真,验证编排的适用性。
3.1 中高纬度导航实测数据解算结果对比分析
中高纬度地区采用北纬60°附近海域24 h激光惯导 IMU实船试验数据,选取的数据初始位置为(56.92°N, 19.43°E),初始北向速度为 20.17 m/s,初始东向速度为4.68 m/s,初始航向角为18.66°,初始横摇角为 0.24°,初始纵摇角为 0.96°。分别基于传统地理坐标系编排与基于统一横向坐标系编排进行惯导解算,其结算差结果见图3。
仿真结果为两种惯导编排的解算差,其误差特性与单一惯导编排误差特性不完全相同。通过比较两种编排结果数值大小的相近程度验证统一坐标系编排的正确性。仿真结果误差的均值和方差统计结果如表1所示。
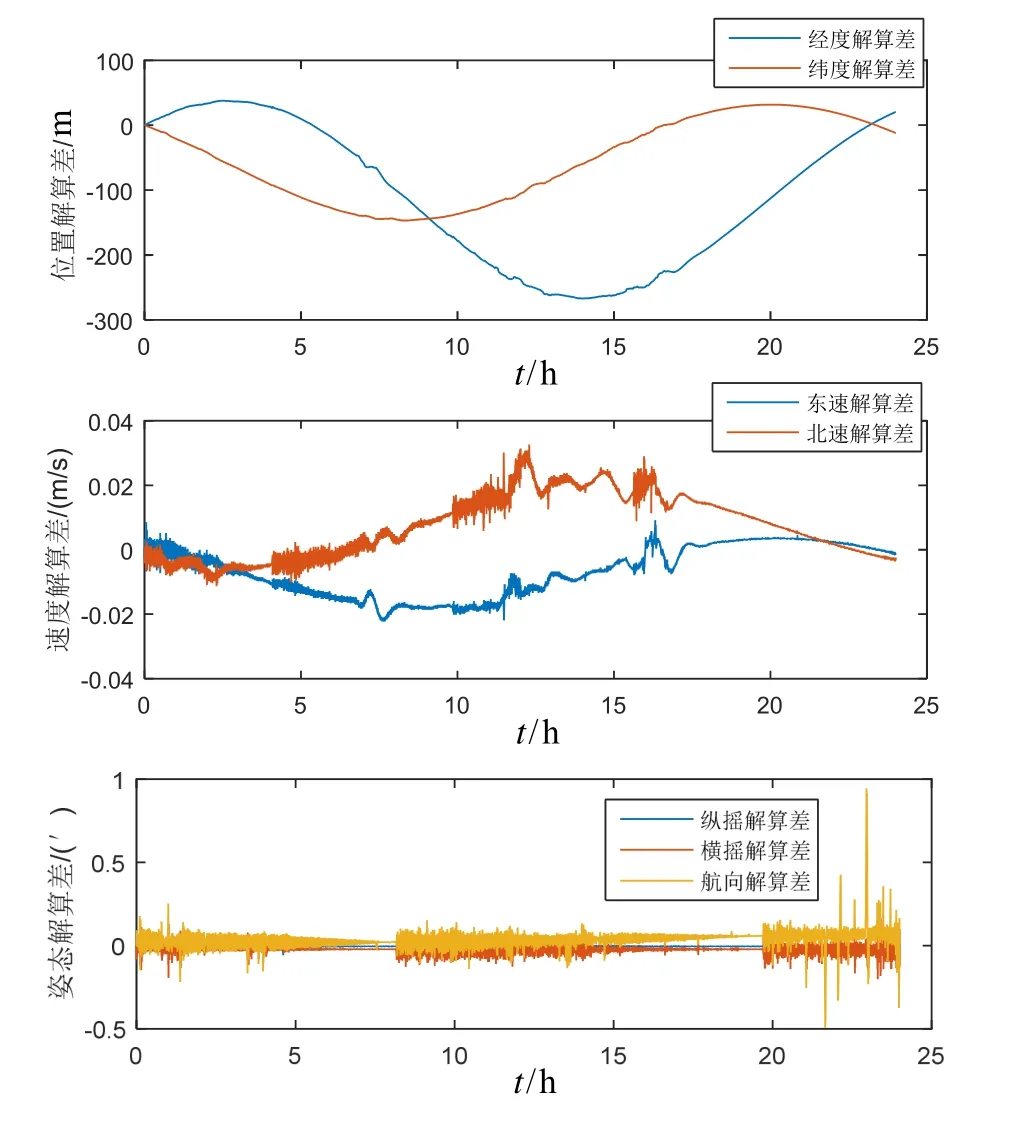
图3 中高纬度统一横向坐标系编排与传统地理坐标系编排解算差仿真结果Fig.3 The difference of solution between the unified transverse coordinate system and the traditional geographic coordinate system in mid-high latitude area
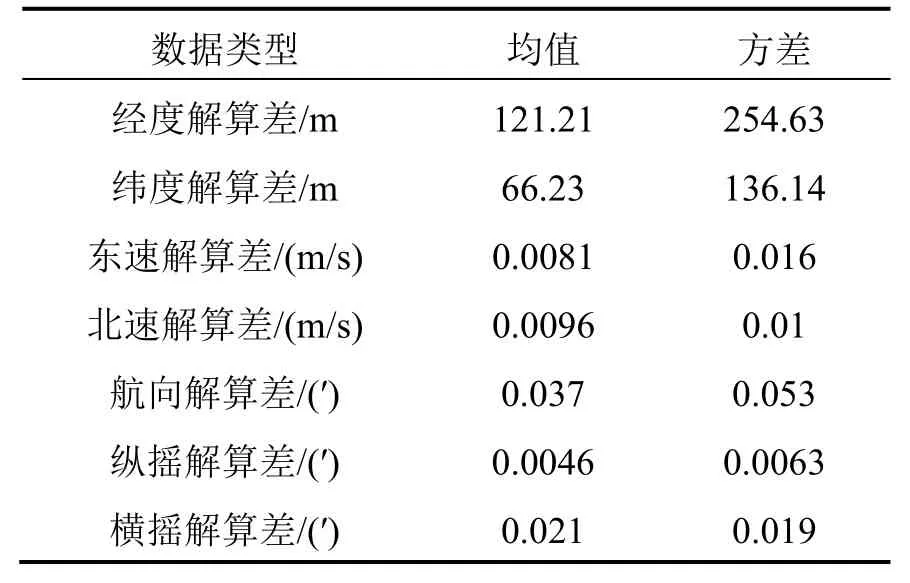
表1 中高纬度仿真结果统计值Tab.1 Statistics of simulation results in mid-high latitude area
结合以上结果可知,中高纬度统一横向坐标系解算性能与传统地理坐标系解算性能整体趋势一致,两者解算差值在可接受范围,即统一横向坐标系编排与传统地理坐标系编排同样适用于中高纬度地区。以此可验证统一横向坐标系的导航编排的正确性。
3.2 极区导航仿真结果对比分析
假设载体初始地理位置为(88°N, 125°E),航行速度为 15 m/s,航向角为 0°,横摇角设置为 0.3°sin(πt/4),纵摇角设置为0.3°sin(πt/4),仿真周期为48 h。在轨迹发生器中将三个陀螺的常值漂移为 0.001 (°)/h,随机白噪声标准差为0.001 (°)/h,三个加速度计零偏为10-5g,随机白噪声标准差为10-5g。仿真结果如图4所示。
根据图4极区统一横向坐标系编排结果,可直观得到其极区性能:1)纬度误差、经度误差在 2000 m以内;2)东向速度、北向速度误差不超过2 m/s;3)横、纵摇误差不超过1′,航向误差不超过3′。
由此可知,在极区通过仿真所得误差结果 48 h内各项误差符合惯性元器件引起的系统误差发散规律,满足极区导航的要求,可验证统一横向坐标系的导航编排在极区的适用性。
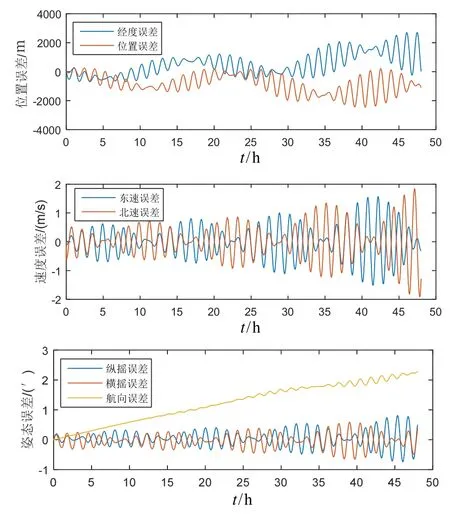
图4 极区统一横向坐标系编排仿真结果Fig.4 Simulation results of the unified transverse coordinate system in polar region
4 结 论
本文提出了一种基于椭球统一横向坐标系导航方法,采用与格林尼治格网坐标系统一的横向坐标系的定义,实现了横向坐标系和格网坐标系两类极区导航坐标系的统一,同时也可实现与横向墨卡托海图格网坐标系的极区应用的统一。这一坐标系可使不同导航系统间参数转换更加便捷,为极区多种导航系统坐标系和坐标参数的统一提供理论基础。通过解决新统一横向坐标系基于地球椭球模型下的横向经纬线不正交的问题,推导出极区惯导算法编排。并通过中高纬度地区惯导实测数据和极区仿真数据验证了新统一横向坐标系下的极区惯导算法的有效性和适用性,可为惯导极区导航控制方法提供参考。
