北斗站间单差载波相位差分定位方法

李 亮，陈 晶，冯 帅，贾 春

（1.哈尔滨工程大学 自动化学院，哈尔滨 150001；2.海军研究院，北京 100073）

高精度和高可靠性的实时定位一直是卫星导航领域的研究热点[1]。由于伪距观测量的测量精度较低，高精度（分米级甚至厘米级）定位通常基于载波相位差分定位技术实现[2-4]。在卫星原始观测信号中存在大量误差项，如：电离层与对流层延迟等大气误差、卫星与用户端偏差、多径误差等，当基线距离较短时（如少于 20 km），误差具有空间相关特性，通过差分即可将误差消除或减弱。RTK（Real-time Kinematic）技术利用观测量差分思想，有效满足了实时、精密、高效的定位需求[5-6]。常规RTK技术采用站间-星间双差，分别消除了卫星端偏差项、大气误差项及接收机端偏差项，恢复了相位模糊度整周特性，具有高精度定位能力。但双差模型仍存在一定局限与不足。观测量站间-星间双差不仅将观测量噪声放大了2倍，还使得在星间差分中，非参考卫星需要与参考星进行差分来消除与接收机相关的误差，这就导致了所有双差观测量中均引入了参考观测量的误差，产生了误差耦合问题。这种误差耦合问题会影响系统的定位精度与可靠性，例如当参考观测量存在粗差或偏差干扰，会将该误差传递给所有差分观测量中，从而影响定位误差及可靠性性能。不仅如此，当前后历元之间传递双差模糊度所对应的参考星不同时，还需要构造一个转换矩阵，用于将双差模糊度“映射”到当前历元的参考星，以确保传递的准确性与滤波的连续性。在时频传递应用中，双差模型由于前后历元参考星发生变换，将会导致时频传递中存在两参考星的双差模糊度差量，引起时频传递的“整周跳跃”[7]。如果双差模型实现绝对定位，还需要获取基站位置，这有可能会暴露基站坐标。

为了解决以上双差模型存在的问题，提出一种基于站间单差模型的精密定位方法。在基站端设计新的修正参数播发参数，无需包含基站位置信息。在用户端接收基站的修正参数，进行站间差分操作，消除卫星、大气延迟等误差，保持卫星间观测量的独立性。由于在单差模型中接收机端部分误差项并未消除，其中除了存在的接收机钟差外，伪距观测量还包含有接收机硬件延时误差，相位观测量还包含有相位偏差破坏了模糊度的整周特性。Collins在实验中发现伪距偏差与相位偏差的数值上存在不一致部分[8]。因此，有必要采用双钟差模型，设置两种接收机钟差状态量对两种不同观测量进行去耦处理[7,9]。

本文首先给出基于站间单差模型的导航定位算法在基站与用户端的函数模型与随机模型；随后构建基于扩展卡尔曼滤波估计量的系统模型与观测模型；最后通过实测车载实验，对改进模型进行验证分析。

1 基于站间单差的精密定位算法

1.1 基站端播发修正策略

基站端接收机的原始伪距、相位的观测模型可以表示为：

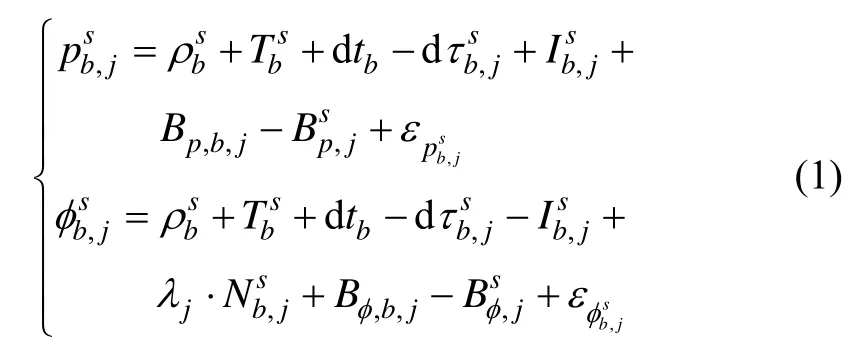
式中，下标b、j与上标s代表基站、频率和卫星；p和φ分别表示伪距和相位的原始观测值；ρ表示接收机到卫星的几何距离；T表示为对流层延迟；dt和dτ分别表示接收机钟差和卫星钟差；I表示电离层延迟；与B有关的项表示由硬件延迟、初始相位等引起的距离偏差，其中Bp,b,j和分别表示接收机端和卫星端的伪距偏差，Bφ,b,j和分别表示接收机端与卫星端的相位偏差；λ表示相位波长；N表示整周模糊度；与ε相关的项均表示观测噪声等影响。

在基站观测模型中，由于基站坐标位置已知，站星几何距离ρ可以准确求解。考虑到基站与用户所处海拔高度可能不同，对流层延迟干扰不具有强相关性，有必要采取Saastamoinen模型对其进行预测修正[10]。观测模型中包含的卫星钟差可以利用广播星历中钟差参数进行修正。对式(1)进行整理，可以得到：

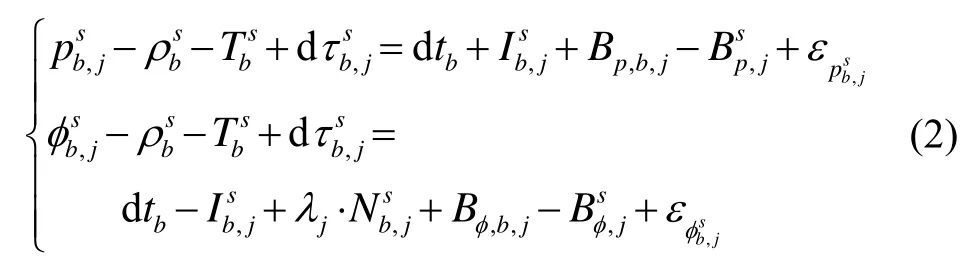
将式(2)中全部的未知误差项统一作为基站播发的综合修正项δp、δφ播发给用户，其修正项可以表示为：

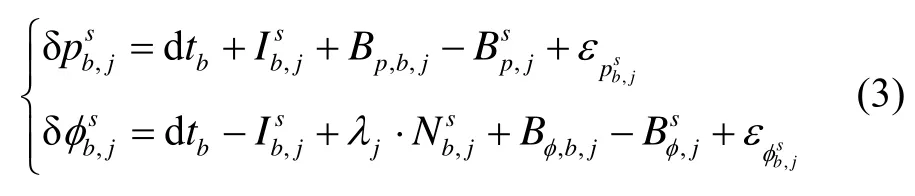
1.2 用户端的函数模型

用户端接收机的原始伪距、相位的观测模型可以表示为：

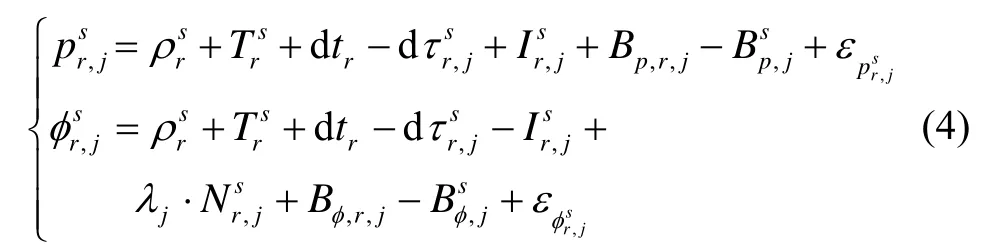
其中，下标r表示用户。用户端接收基站播发的综合修正参数δp、δφ，在原始观测模型中进行站间差分，对流层与卫星钟差同样采用模型修正。因此，用户端的站间差分修正模型，可以表示为：

由式(5)可以看出，接收机端偏差B的存在，是影响函数解算的关键。为了消除偏差作用，在模型推导之前，先定义两类接收机钟差：

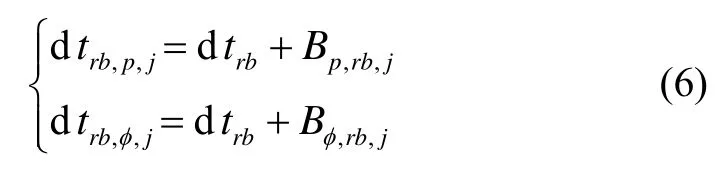
其中，dtrb,p与dtrb,φ分别表示伪距与相位的接收机钟差。需要注意，dtrb为实际钟差，而dtrb,p与dtrb,φ为定义的接收机钟差，包含了偏差项的影响。对于式(6)中下标j是代表不同频率的观测量，因而，dtrb,p,j与dtrb,φ,j代表不同频率的伪距与相位的接收机钟差。式(6)就是将不同频率不同观测类型进行接收机钟差去耦处理的函数模型，处理原因是函数模型只执行站间单差，消除了星端的偏差项，却未消除接收机端偏差干扰，而且接收机端伪距偏差与相位偏差存在不一致部分，如果采用常规单一钟差处理，将会破坏模糊度参量的整周特性，因此，为了恢复模糊度整周特性，实现厘米级的定位精度，有必要采用双钟差估计模型。将 dtrb,p与dtrb,φ两类钟差作为状态量独立估计。

1.3 基于站间单差模型的扩展卡尔曼滤波器设计

在上述对基于站间单差模型的理论分析中，基站端通过算法预处理，计算综合误差修正项作为信息播发策略，降低了通讯链路负担。用户端采用站间差分修正模型，并采用双钟差方式，恢复模糊度整周特性，通过整数最小二乘去相关（LABMDA）模糊度固定算法，输出高精度的导航结果。图1给出了具体的结构。

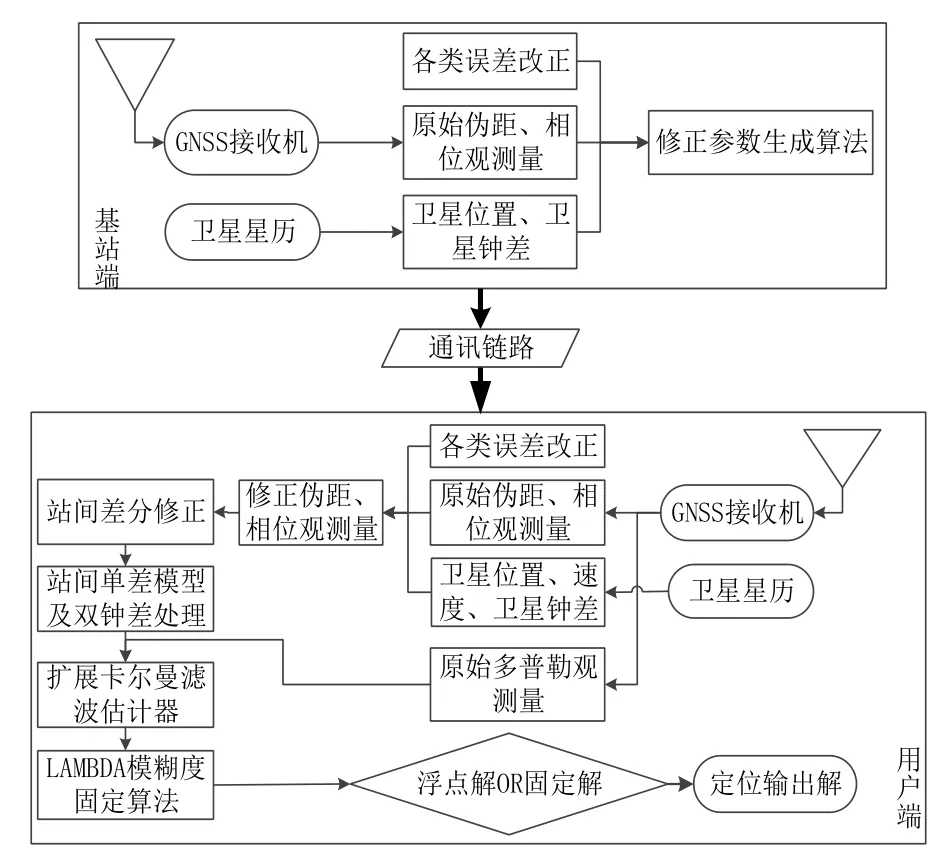
图1 站间单差模型的执行流程图Fig.1 Implementation of SD model

在上述对站间单差模型的详细分析中利用扩展卡尔曼滤波估计器（Extend Kalman Filter，EKF）作为系统的状态估计[11]。以单频系统为例，其相应的估计参数有接收机三维绝对位置、三维速度(动态)、伪距接收机钟差、相位接收机钟差、接收机钟漂、单差模糊度。滤波处理中选取的状态向量为：

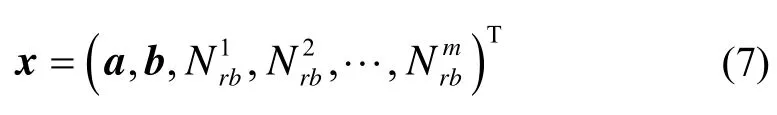
式中，a=(x, y, z, vx, vy, vz)为接收机三维位置与速度，静态条件下接收机三维速度约束为零；b=(dtrb,p,dtrb,φ, dfrb)为相应的接收机伪距钟差、相位钟差与接收机频漂，由于伪距偏差与相位偏差具有短期稳定性，不随时间变化，因而设计一个频漂状态量是合理的；Nirb为单差模糊度，m表示可视卫星的数量。其中状态估计具体方法如表1所示。

表1 状态估计方法Tab.1 State estimation

系统选取的量测量为每颗可视卫星的站间单差伪距与相位观测值，如下：

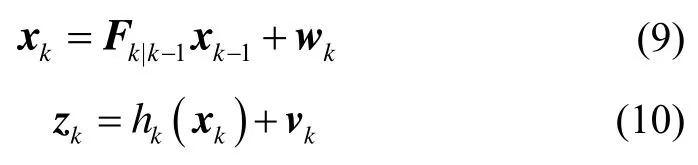
式中，hk的形式如式(5)和式(6)所示，下标k代表第k个历元。将非线性量测函数hk围绕滤波值展成泰勒级数，并略去二阶以上项，得到：

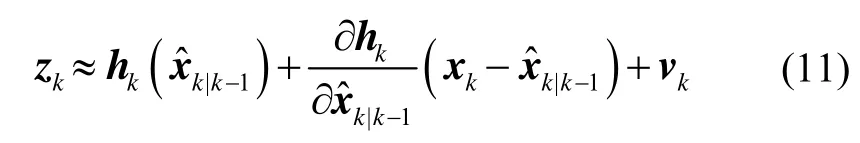
其中，

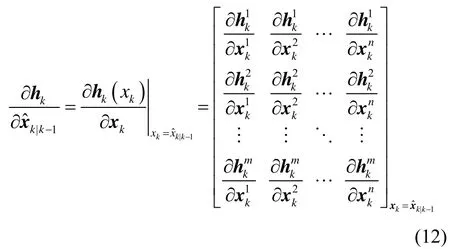
其中

令

则将非线性量测函数式(10)一阶线性化后得到量测方程为

式中，I表示单位阵，静态模式时，A=03×3，B=03×3，C=[1, 0; 0, 1]；动态模式时，A=TsI3×3，Ts是状态方程的差分步长，在这里也等于测量过程的采样时间间隔，

式中，G3×1=(L,M,N)表示接收机到卫星的观测向量三个方向上的余弦向量。G3×m表示接收机到m颗卫星余弦向量所构成的矩阵。

2 实验处理与分析

2.1 实验数据与实验条件

本文所提算法致力于实时高精度导航定位领域，采用单历元瞬时定位模式来实现。由于我国北斗卫星导航系统已经具有亚太区域定位能力，本文利用北斗双频接收机开展动态车载实验。实验的基线长度覆盖4.3～9.5 km范围内，差分用户接收机安置于试验车内。为了有效评估其动态性能，其定位参考值采用商业软件（Inertial Explorer）进行后处理，标称精度达 5 cm(1σ)。其动态测试的轨迹图如图2所示。

图2 动态测试轨迹图Fig.2 Kinematic test trajectory

需要说明的是，在对数据进行处理时，设置卫星截止高度角为20°，以尽量剔除低精度、强多径的观测值。为进一步均衡各观测量的测量精度，还应考虑各个观测量的加权系数，加权系数表示了各个观测值在系统模型的权重，正确选择权值是至关重要的。这里选择一种通常采用的卫星高度角加权模型，其表现形式为

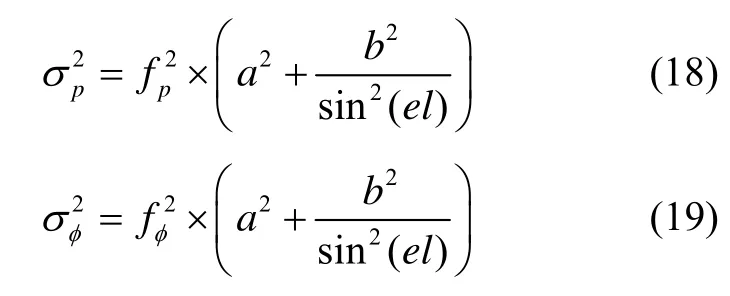
式中，、分别表示相应载波相位和伪距与高度角相关的方差大小，fp、fφ分别为相应系数，fp=100，fφ=1，a与b为载波相位观测噪声均取为0.003 m，el为卫星高度角。

2.2 结果分析

为了验证改进算法的性能，实验以常规RTK双差模型为算法对比，在固定解以及固定解+浮点解两种定位模式下，从定位精度与模糊度固定率两方面进行定位性能的综合评估。利用导航算法输出的定位结果与参考值的差值作为统计值，采用标准差（STD）与圆概率（SEP95%）统计信息作为定位精度的评定指标。其中，模糊度解算采用LAMBDA算法，比率检测门限设定为3[12]。图3给出两种定位算法的定位误差曲线，表2描述了两种定位算法的误差统计结果，其中DD-RTK表示为常规双差模型RTK技术，SD-RTK表示为改进型站间单差模型RTK技术。

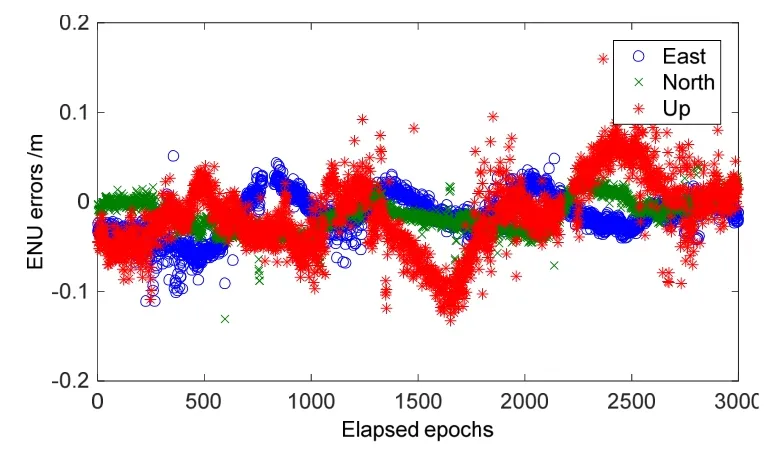
图3 (a) SD-RTK的动态误差曲线Fig.3 (a) Kinematic errors of SD-RTK

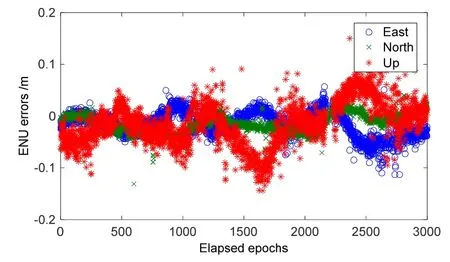
图3 (b) DD-RTK的动态误差曲线Fig.3 (b) Kinematic errors of DD-RTK

从表 2固定解+浮点解定位模式的定位误差统计SEP(95%)可以发现，SD-RTK算法精度较高，而DD-RTK算法受噪声影响相对较大。其原因在于动态原始数据观测量的噪声较大，改进的单差模型仅放大噪声倍，而双差模型将噪声干扰放大2倍，组合观测噪声的放大效应影响了定位精度。从表2中动态实时定位结果中固定解定位模式下东北天方向的STD统计信息可以看出，SD-RTK与DD-RTK的定位精度基本一致。这是由于虽然 SD-RTK可以抑制双差噪声放大的影响，但是基站用户端间的单差偏差难以消除，因此噪声抑制所带来的定位精度提升被未消除的站间单差偏差所抵偿。在模糊度固定率上，SD-RTK也具有与DD-RTK相同的性能。

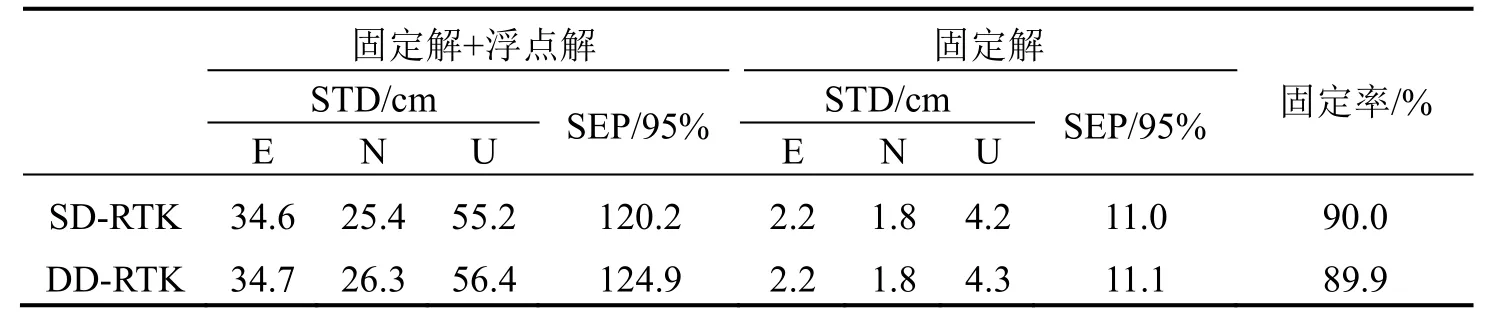
表2 三组实验定位误差的统计分析Tab.2 Three statistical analysis of positioning errors

改进算法经站间单差后，基本消除了星端、大气延迟等误差，并通过LAMBDA算法求解相位的整周模糊度。由此，在恢复相位的整周模糊度后，可以利用式(20)提取出伪距与载波相位不一致部分δtrb,pφ,j：

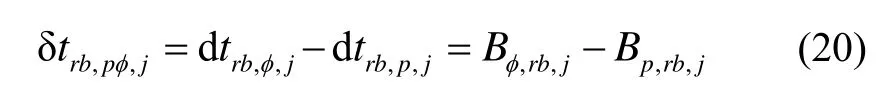
图4给出了整个动态测试中伪距与载波相位不一致部分的变化曲线，其标准差为5 cm，均值为2 cm，厘米级的误差干扰，会影响模糊度的固定性能。因而，在式(7)中采用双钟差模型是有必要的。

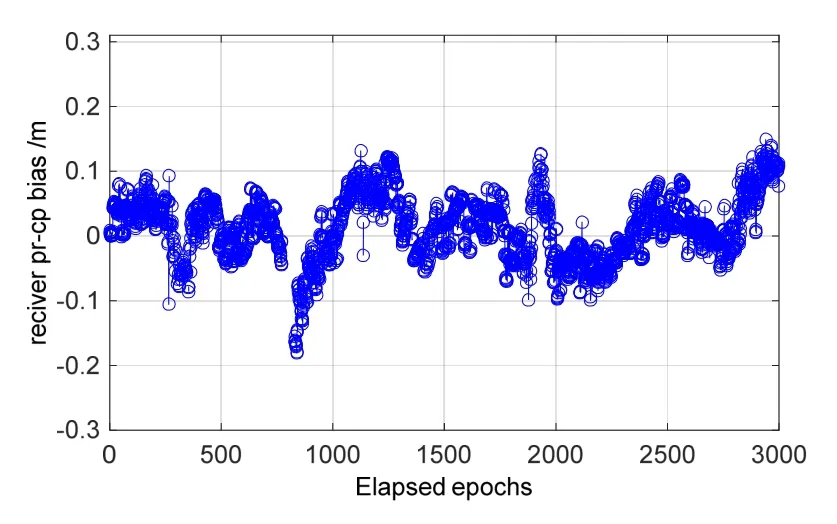
图4 接收机端伪距与相位偏差差值曲线Fig.4 Difference receiver-between phase and code bias

3 结 论

本文分析了传统双差模型在观测误差放大，参考星变化导致整周跳跃的问题，提出了一种基于站间单差的精密定位方法。通过实测车载实验对算法的验证，结果表明改进的站间单差模型具有与双差模型具有相同的定位与模糊度固定性能，在短基线能够达到厘米级定位精度。