智慧导学,让学生循序建构数感
2018-12-19王雪飞
王雪飞
【摘 要】学本课堂并非弱化教师的作用,而是对教师提出了更高的要求。在数概念的教学中,教师可以通过智慧导学,适时把握导的契机,在学生对核心概念的理解处,在学生学习的难点处,在学生对思想方法的感悟处进行导学,从而引领学生经历数概念的形成过程,循序建构数感。
【关键词】智慧导学;数概念;数感
人教版“1000以内数的认识”是“万以内数的认识”的起始部分,它上承一年级下册“100以内数的认识”,又是后面认识更大的10000以内数的基础,它是第一学段的一节数概念课。如何在数概念的教学中通过教师的智慧导学,引领学生深入理解数的意义,充分感受和体验数概念的形成,让学生循序建构数感,我们进行了实践与思考。
一、导在学生对核心概念的理解处
“万以内数的认识”是认数的第三阶段,但它的基本原理始终是“十进制计数法”,十进制计数法的核心就是“满十进一”的进位制和位值制,如果學生对进位制和位值制缺乏理解,则数感难以建立,必然导致后续认识较大数和较小数时出现严重的障碍。第一学段的学生思维形式已经慢慢从形象思维向抽象思维转变,但在形成抽象思维的过程中,仍然需要借助大量的直观形象事物的支撑。所以在教学中笔者借助几何模型和计数器,紧紧抓住“满十进一”这个关键处,不断丰富对“十进制计数法”的感性认识,帮助学生积累数感经验。
【教学片段一】认识“千”和“千位”,感知十进关系
师:桌面上所有的正方体合起来一共有几个?同桌合作数一数。(学生活动)
师:谁愿意把你们的数法和大家分享一下?(指名学生上台一边数,一边贴)
师:你们是怎么数的?
生:我们是一百一百地数,10个一百就是一千。
师:想象一下,这1000个小正方体叠起来会是什么形状呢?(先让学生闭眼想象,再课件演示)
师:回顾一下,刚才我们是怎样数小正方体的?(随着学生的回答教师贴图片)
师:一、十、百、千都是计数单位,如果我们把一个大面包看成一千,那么同学们想一想,面包粒、面包条、面包片分别代表多少?
学生闭上眼睛想象4个计数单位。
师:仔细观察这4个计数单位,说说它们之间有什么联系。
生:10个一是十、10个十是一百、10个一百是一千。
师:像这样,我们就说每相邻的两个计数单位之间的进率是10。
(出示计数器)学生操作:一个一个地拨,十个十个地拨,一百一百地拨,拨到1000。
师:在刚才拨珠子的过程中,你有什么发现?
生边拨珠边说:个位满十向十位进1,十位满十向百位进1,百位满十向千位进1。
师:这就是我们平常所说的“满十进一”,“千位”就是计数单位千所在的位置。
在充分数小正方体的过程中,经历一而十,十而百,百而千,感受“条(十)”“片(百)” “体(千)”的过程,帮助学生建立一、十、百、千的几何模型,引导学生根据直观模型的变化,由点—线—面—体,通过物象的强化,建立起“位次”感,即前一位的大小是后一位的10倍,为学生系统认识计数单位,以及相邻两个计数单位的十进位关系积累了感性经验。然后顺势让学生在计数器上拨一拨,思考“刚才拨珠子的过程中,你有什么发现?”一个看似简单的问题,实则直指数概念教学的核心,引发学生思考的欲望,让学生自主发现个位满十向十位进1,十位满十向百位进1,百位满十向千位进1,夯实学生对计数单位和数位的认识,进一步深化对“十进制”思想的感悟。
二、导在学生学习的难点处
正确数出接近整百、整千的数是本节课的难点所在。为了使学生充分理解和掌握拐弯数的知识,教学中笔者遵循由直观到抽象、由易到难、由点到面的原则,让学生充分操作、充分数数,在交流总结中帮助学生突破学习难点。
【教学片段二】数数,突破拐弯数的难点
师:一个一个地数出306后面连续的5个数,有困难可以借助计数器,数给你的同桌听。
生:307、308、309、400。(其他学生纷纷举手)
生:309的后一个数应该310。(请学生到计数器上拨一拨)
生一边拨一边说:再拨一个,个位满十向十位进1,309的后一个数是310。
师:一个一个地数,309的后面是310,你能想到3□9的后面一个数是多少吗?说给同桌听。
生①:329的后面是330,359的后面是360。
生②:499的后面是1000。(其他学生纷纷举手)
请这位学生上台到计数器上拨一拨,一边拨一边说:个位满十向十位进1,十位满十向百位进1,499的后面是500。
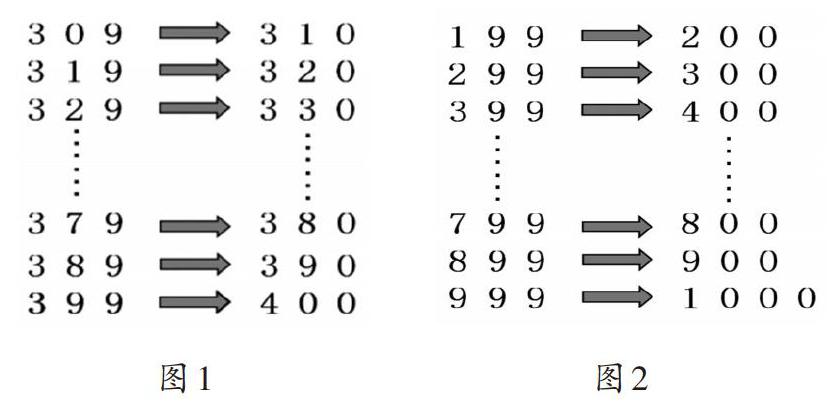
师:3□9的后面是多少,谁能把所有的都说出来?
学生口答,课件出示:
师(追问):数得这么顺溜,有什么秘诀?
生:我的秘诀是9的后面是10 ,所以309 的后面就是310,19的后面是20,所以319 的后面是320……
师:你真善于思考,把1000以内的数数转化成100以内的数数。把新知转化成旧知是学习数学的一种重要方法。
师:一个一个地数,399的后面是400,你能想到□99的后面是多少吗?
师:□99的后面是多少,谁能把所有的都说出来?(学生口答,课件出示图2)
师(追问):你又有什么发现?
师:如果从800往后十个十个地数,你会数吗?你怎么想到890的后面是900?
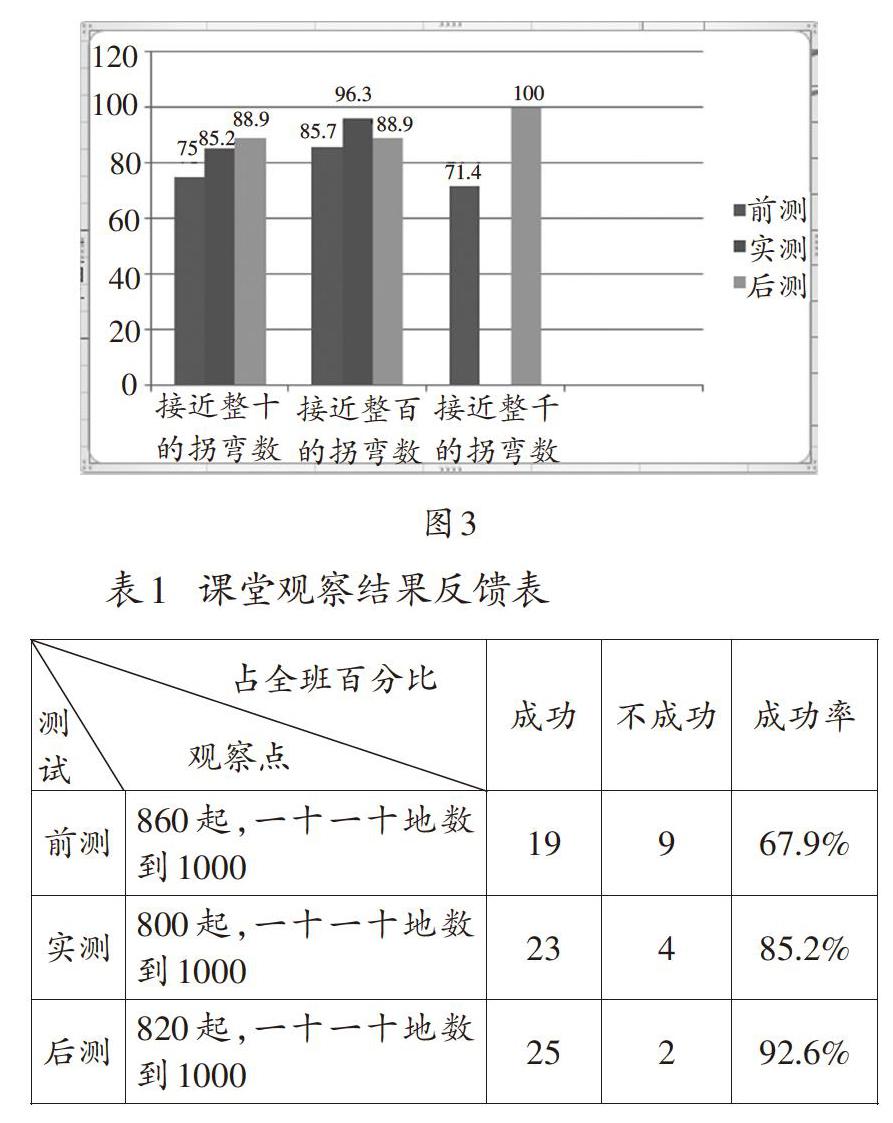
教学中以309的后一个数是310为突破口,推想3□9的后一个数是多少,继而推想出□99的后一个数是多少,然后利用计数单位“十”,一十一十地从800数到1000,当学生出现困难、出现错误时,教师没有一带而过,而是放慢节奏让学生动手拨、动口说、动脑想,在慢镜头中突破1000以内数拐弯数的难点。在此基础上,对接近整十、整百、整千的拐弯数的多个数组进行整体梳理,引导学生对数拐弯数的方法适时总结,很好地化解了教学的难点,同时又让学生在发现规律中深化对满十进一的再认识。整个数数的过程,为学生提供了充分的自主探究空间,问题导引、由扶到放、动静结合、学思并重,在学会数数的基础上,有效悟得1000以内数的顺序,内化了学生的数感。由课堂观察和课后测数据(见图3)可见,学生的数数成功率全程呈上升趋势,教师的“导”起到了举足轻重的作用。(见表1)
这是我们的课堂实测与后测:
三、导在学生对思想方法的感悟处
数学思想方法对于学生而言不是仅靠教师的教就能习得,而是需要学生经历一个从模糊到清晰、从理解到应用的过程。因此,在教学实践活动中需要教师把握契机,引导学生在主动探究数学知识的过程中,领悟数学思想方法。
【教学片段三】感受1000的大小
师:这是1根小棒,想象一下1000根小棒有多大一捆?用手比畫一下。
师:差距有点大。
师:这是100根小棒,现在你觉得需要重新调整一下吗?(学生调整后基本接近)
师:(出示1000根吸管)估计一下有几根?为什么?
生:10000根。
生:2000根。
师(一手拿1000根小棒,一手拿1000根吸管):仔细观察,估计一下有几根?
生(不由自主地喊):1000根。
师:你是怎么想的?
生:因为吸管比小棒粗。
师:对,一根吸管所占的空间比一根小棒大,所以1000根吸管所占的空间就比1000根小棒所占的空间大。
师:这是100粒黄豆,老师把它倒在了这个圆柱形的罐子里。如果装满这个罐子,大约有多少粒黄豆?
师:你是怎么估计的?
生:用尺子量一量这100粒有几厘米高,再数一数有这样的几份。
课件出示线段,用尺子来量一量、数一数,大约有几个这样的百?
生:100、200……1000。
师:装满这个罐子大约需要1000粒黄豆。看,就是这样的一罐(出示满罐的黄豆)。
对于1000的大小,学生对具体数量的感悟还是比较模糊的,笔者借助1000个小立方体、1000根小棒、1000颗黄豆、1000个座位等学生身边熟悉的事物,激活学生原有的生活经验。在估计的过程中没有让学生单纯地估,而是进行充分的猜测、估计、交流,不断反思和调整自己估数的方法,让学生经历随意猜到根据以“百”为标准进行估的过程,领悟合理估测大数的思想方法,发展学生的数感。从课堂观察中可以看到,在教师的引导下,学生对1000数量大小的建立效果是明显的(见表1)。同时,有机渗透了数形结合的思想方法,100粒黄豆用一条线段来表示,1000粒黄豆就是这样的10段,把具体的数量抽象成“形”,从“形”的角度进一步感知数、认识数,帮助学生丰富自己的数感经验,形成对1000数量大小的观念,从而建立数的概念。
学本课堂并非弱化教师的作用,而是对教师提出了更高的要求,教学中要进一步做好智慧导学,适时把握导的契机,让学生经历数概念的形成过程,循序建构数感。
参考文献:
[1]戴银杏.学本课堂——小学数学课堂教学案例与反思 [M].北京:光明日报出版社,2017.
[2]吴汝萍.让数感在认数过程中“丰满”起来[J].河北教育,2012(10).
(浙江省天台县外国语学校 317200)
