极化码的参数捷变技术及性能仿真
2018-12-19
(西安烽火电子科技有限责任公司,西安 710075)
1 引 言
随着通信系统的迅猛发展以及互联网在国民生活中的普及,人们对通信的需求正在发生变化,从最初的语音通话逐渐向综合业务方向发展,如视频点播、互动直播等多媒体业务,同时参与者的通信需求、通信时间、通信位置均变得越来越随机。在这种随机的情况下,为了实现可靠通信,发送方需要根据其与接收方之间的实际通信环境与业务需求实时改变数据传输速率。为解决这一问题,可以在信息发送端进行不同码率的信息编码。例如第3代(3G)与第4代(4G)移动通信中均采用了码率为1/3、1/2和2/3等信道编码方案。当实际的通信环境较好、信道质量较高时,发生错误的概率较低,可以在信息比特后添加少量校验位(高码率编码)来克服传输过程中可能出现的少量错误;反之,就要在信息比特后添加大量校验位(低码率编码),因为此时信息比特经信道传输会以较大的概率发生错误。
在实际应用中,码率类型越多有效性就越高[1]。然而,众多的码率类型无疑增加了收发两端的编译码复杂度,同时降低了系统整体的可靠性。因此一般的做法是制定几种常用码率,当需要其他码率时,通过一些方法(如打孔、添加已知序列等)在常用码率的基础上进行变化得到。在编译码领域将能够快速灵活地改变编译码参数的策略称为参数捷变编译码技术,此项技术使得编译码器能够随通信环境的变化而快速、灵活地改变自身的编码(码长、码率)参数,在最大化利用信道资源的情况下尽可能地提高有效性与可靠性。
极化码(Polar Code)[2]由土耳其的Arikan教授于2008年首次提出,是一种基于信道极化现象构造的码,且是目前唯一可理论证明能够达到二元输入离散无记忆信道(Binary-input Discrete Memory-less Channel,B-DMC)容量的信道编码方案。文献[3]指出,当采用串行抵消列表(Successive Cancellation List,SCL)译码算法时,极化码的整体性能在某些应用场景下取得了和当前最先进的信道编码技术如低密度奇偶校验(Low Density Parity Check,LDPC)码[4]、Turbo码[5]相同甚至更优的性能。在2016年11月结束的第5代(5G)移动通信控制信道短码方案讨论中,中国主推的极化码方案毫无悬念地从美国主推的LDPC码、法国主推的Turbo码两大竞争对手中脱颖而出,成为5G控制信道编码方案。然而,由于极化码的极化特性限制了其码字长度为2的幂次,从而限制了极化码在工程上的应用。
针对上述弊端,本文给出了基于极化码的参数捷变编译码技术,在不改变编译码器硬件结构与程序的情况下仅通过读取配置文件就能够实时、快速地改变编译码参数,以适应各种通信环境与用户需求,具有简单、快速、易实现等优点。
2 极化码的表示
2.1 信道极化现象
信道具有极化特性,类似于社会学中的马修(Matthew)现象。Matthew现象是指“The rich get richer and the poor get poorer(富者越富,穷者越穷)”。体现在信道上是经过某种组合后各个子信道具有不同的信道容量,好的信道会越来越好,趋近于无噪声信道,差的信道会越来越差,无法传输任何信息。因此好的信道适用于传输用户信息,在接收端能够以较大概率恢复。
2.2 极化码的Trellis及其编码


图1 码长为8的极化码Trellis图Fig.1 Trellis of polar code with code length 8
将图1的编码规则改写为矩阵形式有
(x0,x1,x2,…,x7)×F8×Π8=(c0,c1,c2,…,c7)。
(1)
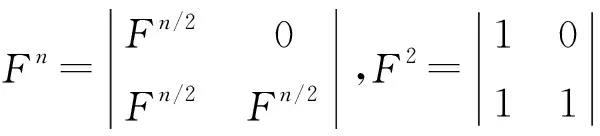
编码时只需要将待编码比特x0,x1,x2,…,xn-1置于Trellis图左边,按照Trellis上的逻辑运算规则从左向右逐级进行计算,即可得到极化码字c0,c1,c2,…,cn-1。从信道的极化特性来看,图1所示的Trellis中8条子信道具有不同的信道容量,例如x7对应的7号子信道的信道容量最大,x0对应的0号子信道的信道容量最小。因此,在编码时需要将待传送的信息放置在信道容量较大的信道上。
2.3 信道的选取
由于每个子信道是具有不同的信道容量,可以依据信道容量从大到小对个子信道进行排序,将前k条子信道作为加载信息(Information)比特的信道,其余的n-k条子信道作为加载固定(Frozen)比特的信道。因此在编码前将待编码比特x0,x1,x2,…,x7划分为信息比特和固定比特。编码时将固定比特设置为收发端事先约定好的比特(如0 bit),依据Trellis图中的逻辑顺序逐级计算从而得到极化码。
需要说明的是,承载信息比特和固定比特的信道选取不是一成不变的,它与信道模型紧密相关,不同类型的信道所选取出的信息信道也是不同的。严格来说,即便都是加性白色高斯噪声(Additive White Gaussian Noise,AWGN)信道,如果传输信道的信噪比(Signal-to-Noise Ratio,SNR)不同,那么加载信息比特和固定比特的信道也不同。对于常用的AWGN信道,可利用密度进化(Density Evolution,DE)理论[7]对信道进行选取。
3 系统极化码
前面介绍的为非系统极化码,即有用信息在码字中是不能直接观测的,而实际的通信系统中经常用到的是系统码,即有用信息在生成的码字中能够直接观测的。系统极化码的编码主要思想如下:将Trellis图右边的输出比特位分为两部分,一部分为系统信息(A),一部分为系统校验(B);相应的在Trellis图左边的输入比特为也分为两部分,一部分为信息比特,一部分为固定比特,如图2所示。

图2 系统极化码生成过程Fig.2 Systematic polar code
系统极化码的编码目的就是在已知系统信息和固定比特的情况下,导出信息比特和系统校验,其本质为求解线性方程组。需要指出的是,Trellis图右边承载系统信息和系统校验的子信道的选取是信息比特和固定比特子信道序号的函数,即A和B的选取是和Information、Frozen紧密相关的。若分配给信息、固定比特的序号改变,则系统信息和系统校验的序号选取也跟随着产生变化。
令(x0,x1,x2,…,xn-1)×Fn=(q0,q1,q2,…,qn-1),由公式(1)可知
(q0,q1,q2,…,qn-1)×Πn=(c0,c1,c2,…,cn-1)。
(2)
若(x0,x1,x2,…,xn-1)中信息比特序号与(q0,q1,q2,…,qn-1)中序号选取的完全相同,则系统极化码对应的线性方程组有唯一解。假设第i条子信道的容量经排序(由大到小)后的序号为j=D(i),则有i=D-1(j)。其中,函数D(·)表示密度进化(DE)过程,函数D-1(·)表示函数D(·)的反函数。例如,图2 所示的Trellis在AWGN环境下子信道容量大小顺序与子信道序号关系如表1所示。

表1 码长为8的极化码子信道容量与序号关系Tab.1 The relationship between capacity and index of sub-channel with polar code length 8
从表1可知,第7条子信道对应的信道容量最大,第6条子信道对应的信道容量次之。编码时可以按照容量由大到小的顺序选取前k条子信道加载信息比特。例如有3个待编码的比特,则选取前3个信道容量较大的信道,即第7=D-1(0)、6=D-1(1)、5=D-1(2)号信道加载的x7、x6、x5为信息比特,则相应的选取q7、q6、q5为系统信息,即Trellis图中的c3、c5、c7应为承载系统信息的比特位。因为
(3)
4 参数捷变编码技术
捷变编码技术中需要处理的主要涉及码率、码长两个重要参数,因此便捷编码技术需要解决的问题有构造码长不变、系统信息长度可变的码字和构造系统信息长度不变、码长可变的码字。
4.1 码长不变、系统信息长度可变的码字
利用密度进化理论对各个子信道的信道容量进行大小排序,并生成配置文件。利用信息比特与系统信息之间的关系生成系统极化码,具体的算法如下:
Step1 生成配置文件F。
Step1.1 新建空白配置文件F,给出码长为n(n=2m)的Trellis图。
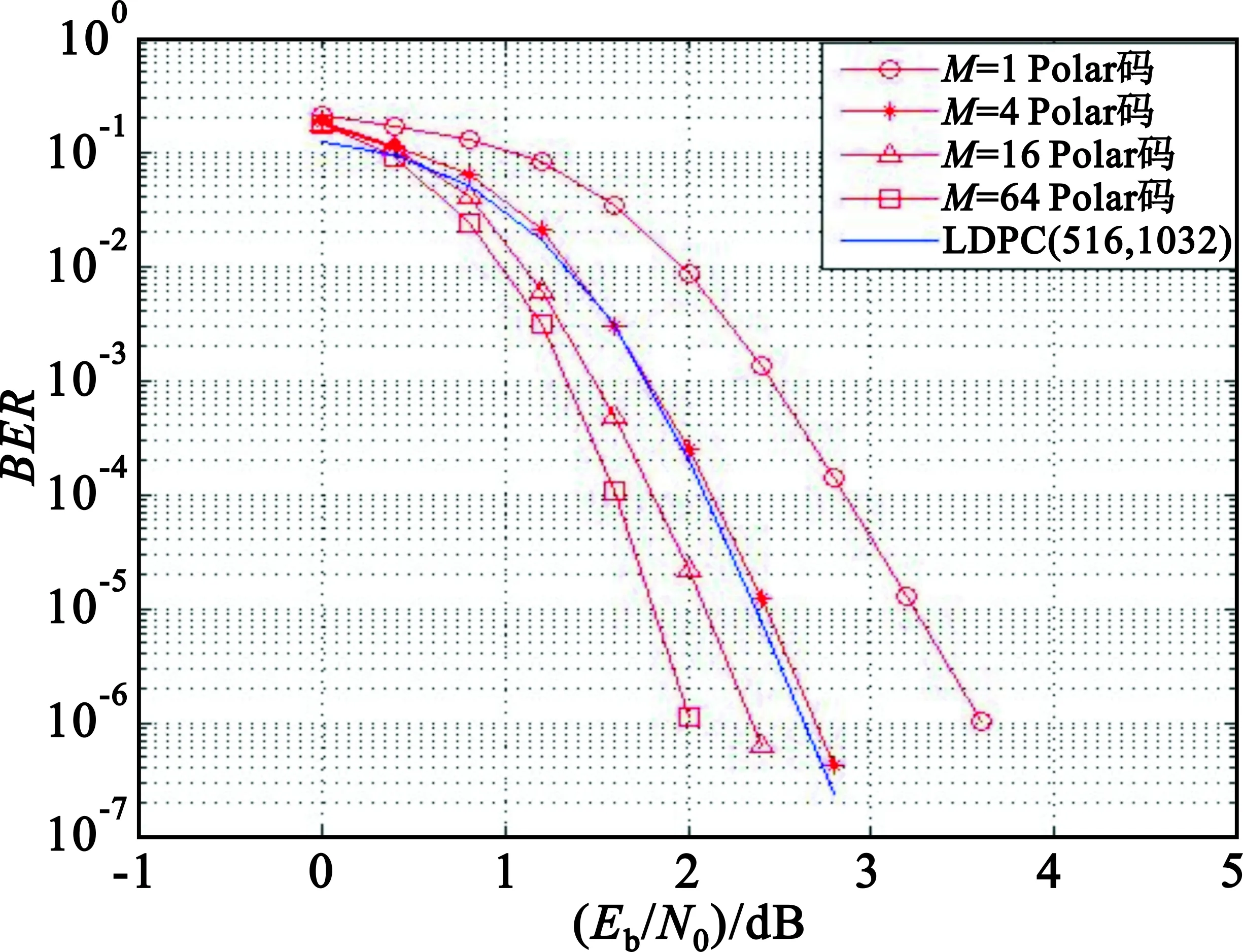
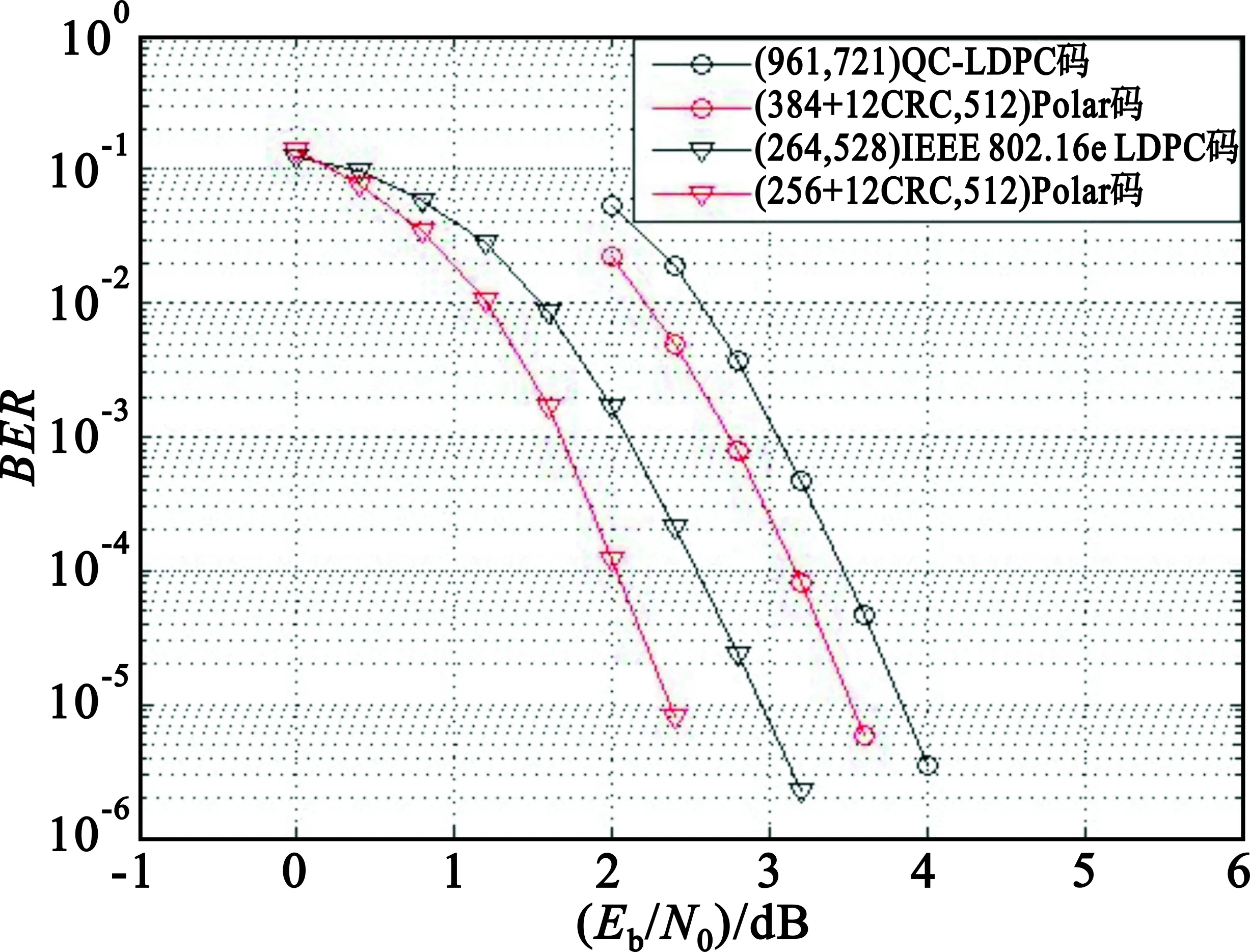
Step1.2 利用DE理论对各个子信道的信道容量进行由大到小排序,第i子信道容量由大到小排序后的序号为j=D(i)(0≤i Step1.3 令j=0, (1)在配置文件F中追加信道容量排在第j位的子信道序号i=D-1(j); (2)j=j+1; (3)若j Step2 系统信息的子信道选取。 Step2.2 构造集合Q={q0,q1,…,qi,…,qk-1},其中,qi=1,若i∈L;否则qi=0。 Step3 生成系统极化码。 Step3.3 令I=0,进行以下迭代过程: (1)按照Trellis上的逻辑运算规则从左向右逐级进行计算; (2)按照Trellis上的逻辑运算规则从右至左逐级进行计算; 系统信息比特个数为k,基码码长为n,则生成码字长度为l(k≤l≤n)的极化码算法(参数捷变的极化编码算法)如下: Step1 生成码长为n(n=2m)的极化码的配置文件F。 Step4 在长度为n(n=2m)的极化码中随机选取n-l个序号,并将对应的比特进行打孔,得到长度为l的极化码字。 极化译码器采用列表(List)译码算法[8]进行译码。List译码是指将可能的码字进行列表,基于表中的码字进行扩展,并利用某种取舍准则从扩展后的列表中抛弃一些不可能的码字,剩余的M个码字组成的列表作为下一次扩展的基列表。极化译码是从第0 bit开始逐比特进行判决/扩展,直到码字的最后1 bit为止。需要说明的是,当M=1即幸存列表中仅有一个幸存码字时,SCL译码算法退化为串行抵消(Successive Cancellation,SC)译码算法。 一般地,在通信系统中会利用循环冗余校验(Cyclic Redundancy Check,CRC)来提高系统的可靠度,也即信息比特序列是符合CRC校验的。极化译码器同样可以利用CRC来提升译码性能,此时译码器的输出准则改为选取置信度最大且能通过CRC校验的码字作为译码器输出,这种算法即为循环冗余辅助的串行抵消列表(CRC Aided SCL,CA-SCL)译码算法。 置信度增量计算是极化译码的重要过程,是基于Trellis图从右向左进行,信息度量为对数似然比LLR(x),它是基于接收值y判断比特取0的概率与比特取1的概率之比: (4) 从极化码的Trellis图上来看,译码器处理的最小单元为一个蝶形,置信度增量计算包括硬信息交换和软信息交换过程,如图3和图4所示。 图3 蝶形单元硬信息交换Fig.3 Hard information exchange 图4 蝶形单元软信息交换Fig.4 Soft information exchange (1)硬信息交换 将幸存码字放置在Trellis的左边,按照Tannr图上的逻辑运算规则从左向右逐级进行计算。 (5) (6) (2)软信息交换 (7) (8) 将计算得到的输出依Trellis的连接传送至前一级,而后对每一个蝶形单元执行信息交换过程。当计算到第0级时,对目标比特进行判决,例如对第i比特进行判决,有 (9) 式中: 第i比特对应的置信度增量计算规则如下: 以下仿真中的信道均为AWGN信道,调制方式为二进制相移键控(Binary Phase Shift Key,BPSK)。 信息位长度512 bit,极化码字长度1 024 bit,极化译码算法采用SC译码算法,仿真结果如图5所示。从图5中可以看到系统极化码与非系统极化码两者的误帧率(Frame Error Ratio,FER)几乎相同,而误码率(Bit Error Ratio,BER)不同,系统码的误码率明显优于非系统码的误码率。例如,当BER=10-5时,系统码需要的信噪比约为3.2 dB,而非系统码需要的信噪比约为3.5 dB,两者之间有0.3 dB的性能差异。由于系统码的性能优于非系统码,因此以下仿真均采用极化系统码进行。 图5 系统码与非系统码的性能比较Fig.5 Comparison between systematic and non-systematic polar codes 信息位长度512 bit,极化码字长度1 024 bit,CRC生成多项式g(x)=x12+x11+x3+x2+x+1,为了简单起见将其记作(512+12CRC,1 024)。同时为了便于比较,也给出了宽带无线接入空中接口标准(IEEE 802.16e)中所采用的码率为0.50的LDPC码字性能。其中,LDPC码校验基矩阵维数12×24,选取扩展因子43,从而得到LDPC码字(516,1 032)。译码采用和积译码算法[9](Sum Product Algorithm,SPA),迭代次数50次,仿真结果如图6所示。 图6 CA-SCL译码算法在不同参数下的性能Fig.6 The performances of CA-SCL decoding algorithm with different parameters 从图中可以看到: (1)幸存码字个数越多,CA-SCL译码算法的性能越好。例如当BER=10-6时,在M=1的情况下所需信噪比为3.6 dB;在M=64的情况下所需信噪比为2.0 dB,两种情况下存在1.6 dB的性能差异。 (2)当M=4时,极化码的性能基本与LDPC码相同;当M>4时极化码的性能明显优于LDPC码。例如当BER=10-6、M=64时,极化码相比于LDPC码可获得约0.55 dB的增益。 使用基码长度为512的极化码进行参数捷变,分别实现码率为0.75的(412+12CRC,512)和码率为0.50的(256+12CRC,512)极化码以及码率为0.33的(150+12CRC,450)缩短极化码,译码算法采用CA-SCL算法,幸存码字个数M=16。为了便于比较,同时给出了编码参数近似相同的LDPC码,分别是码率0.749的大数逻辑可译LDPC码(961,721)[10-11]、IEEE 802.16e标准所采用的码率0.50的(264,528)LDPC码和IEEE 802.16e标准所采用的码率0.33的(150,450)LDPC码,仿真结果如图7和图8所示。 图7 码率为0.75和0.50极化码与LDPC码性能比较Fig.7 Performances comparison between polar and LDPC codes with code rates 0.75 and 0.50 图8 码率为0.33极化码与LDPC码性能比较Fig.8 Performance comparison between polar and LDPC code with codes rate 0.33 从仿真图形中可以看到,当编码参数近似相同时极化码和缩短极化码的性能明显好于LDPC码。例如在BER=10-5时,码率为0.75、0.50和0.33的极化码分别优于LDPC码0.3 dB、0.6 dB和1.3 dB。这里需要指出的是,3个不同参数的LDPC码对应3个不同的校验矩阵,若一个通信系统要使用不同码率的码字,则需要由硬件分别编写3个LDPC的编译码程序。然而对于极化码来说,3个不同参数的码字均由1个基码通过参数捷变得到,收/发两端分别使用1套编/译码器即可完成3个不同参数码字的编译码,大大降低了系统的复杂度,这为极化码在实际的应用带来了便捷。 本文从Trellis的角度对极化码进行了描述,详细分析了极化系统码与非系统码生成过程,介绍了SC、SCL和CA-SCL译码算法,基于凿孔与密度进化理论提出了编码参数捷变技术,能够在不改变编译码器硬件结构与程序的情况下实时、快速地改变编译码参数,不同参数的码字均由1个基码通过参数捷变得到,收/发两端分别使用1套编/译码器即可。仿真结果表明,在高、中、低很宽的码率范围且编码参数近似相同的情况下,极化码的性能要优于低密度奇偶校验码。本文提出的极化编译码参数捷变技术可为极化码在实际通信系统中的应用提供相关的理论参考,更为今后该方面课题的研究提供了借鉴。


4.2 系统信息长度不变、码长可变的码字



5 极化码的译码算法
5.1 译码原理与流程
5.2 置信度增量
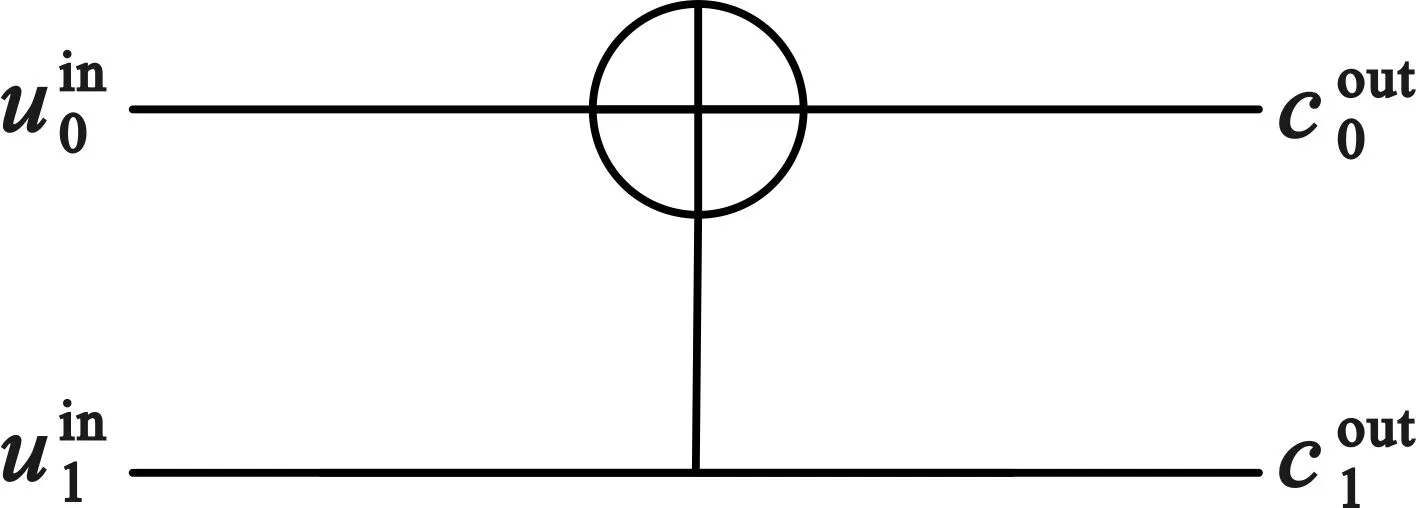
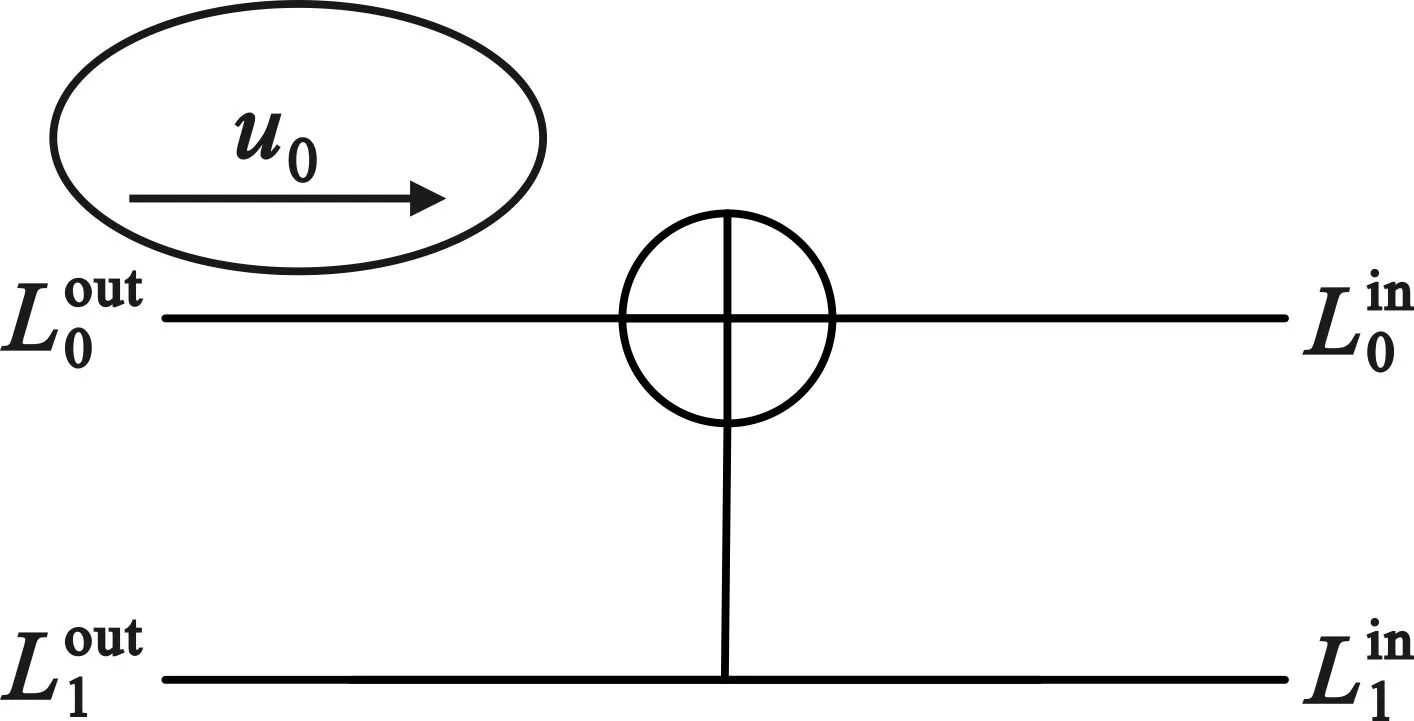

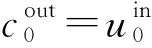


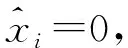

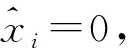
6 性能仿真分析
6.1 极化系统码与非系统码之间的性能差异

6.2 CA-SCL译码算法的性能
6.3 参数捷变的极化码性能

7 结束语
