利用超导量子电路模拟拓扑量子材料∗
2018-12-18喻祥敏谭新生于海峰于扬
喻祥敏 谭新生 于海峰 于扬
(南京大学物理学院,固体微结构国家重点实验室,南京 210093)
(2018年10月16日收到;2018年11月16日收到修改稿)
1 引 言
量子力学是描述微观世界的基本理论,把量子力学应用于凝聚态多体系统,探索新的材料及其物理性质具有重要意义,也取得了很大的成功.但是,随着多体数目及自由度的增大,量子系统的Hilbert空间维度呈指数增加,指数爆炸将导致用经典计算机难以计算量子多体系统.因此,Feynman[1]提出了量子模拟的思想,即通过构建一个人工量子系统模拟量子多体系统,将关于量子多体系统的复杂计算问题转化为控制人工量子系统演化,并测量演化结果的实验问题,从而实现对复杂量子多体系统的间接研究.由于复杂凝聚态系统大都存在自旋-轨道耦合,初期量子模拟主要利用冷原子和光晶格系统[2,3].相比冷原子和光晶格系统,超导量子电路作为全固态器件,在扩展性、集成性、调控性上都具有更大优势[4],超导电路系统在模拟原子分子物理和量子光学方面也取得了巨大成功[5].但是超导量子电路在模拟凝聚态量子材料方面一直是一个尚待开发的领域.随着对超导量子比特研究的不断深入,人们已经可以将退相干时间延长至100µs[6],同时对于超导量子电路的调控也日趋成熟.我们发现可以把凝聚态多体系统的准动量空间映射到调控超导量子比特的微波场参量空间,利用超导量子电路实现其哈密顿量,通过直接测量能谱即可得到决定系统性质的能带结构.利用超导量子电路的高度可控性,可以测量系统的拓扑性质,观测系统的拓扑相变.通过对系统的量子模拟,人们可以研究复杂凝聚态系统的新奇拓扑性质.
本文简要介绍了量子模拟的基本概念、基本类型以及基于超导电路系统的量子模拟方案;介绍了利用超导电路系统对拓扑体系进行量子模拟的基本原理和实验过程;利用超导电路系统模拟拓扑材料的Hamilton量,实现时间-空间反演对称性保护的拓扑半金属、Hopf-link半金属、Maxwell半金属;最后对全文进行了总结,并展望利用超导电路系统研究拓扑材料的前景.
2 量子模拟
自量子模拟的构想提出以来,量子模拟一直应用于可控人工量子系统.量子模拟原理如图1所示,通过在被模拟系统的哈密顿量和量子模拟器的哈密顿量之间建立映射关系,量子系统就可被量子模拟器模拟.根据量子模拟器的演化规律,可以得到被模拟系统的信息.因为人工量子系统的演化自然地服从量子力学规律,模拟量子系统时没有经典计算机那样的限制,故量子模拟器可以处理复杂的量子多体问题.

图1 量子模拟器图解 量子系统经过幺正变换U=exp(−i}Hsyst) 由态演化至态 相应的量子模拟器经过幺正变换U′=exp(−i}Hsimt)由态|ψ(0)⟩演化至态 通过设计量子模拟器,可以在被模拟系统的哈密顿量和量子模拟器的哈密顿量之间建立映射关系,因此量子模拟器的末态将提供被模拟系统的演化信息[6]Fig.1.Schematic of a quantum simulator.The quantum system evolves from the initial stateto the final statevia the unitary transformation U=exp(−i}Hsyst).The quantum simulator evolves from the initial stateto the final statevia U′=exp(−i}Hsimt).One can design the simulator such that there is a mapping between the simulator and the simulated quantum system.As a consequence,the final statewill provide information about the simulated system[6].
量子模拟按原理可分为两种类型:数字式量子模拟(digital quantum simulation,DQS)和模拟式量子模拟(analog quantum simulation,AQS)[7].数字式量子模拟就是用量子位来编码量子态,利用门操作实现量子演化[8].因为任意幺正演化可以由通用逻辑门的组合实现,数字式量子模拟方法原则上是普适的,但是实际上模拟线路一般无法接近真实系统的物理本质,模拟线路与真实系统的接近程度决定了数字式量子模拟的精度.模拟式量子模拟要求量子模拟器和被模拟系统应该有相同的动力学特征(即相似的哈密顿量),因而利用量子模拟器的动力学演化可以研究被模拟系统的物理特性[9].模拟系统和被模拟系统之间映射的准确性是模拟式量子模拟的优势,但是模拟式量子模拟方案通用性比较差,只能够模拟特定类型的量子系统.
可以被用作量子模拟器的量子系统需要满足Cirac-Zoller判据[10]:1)量子系统,即量子模拟器是一个具有多自由度的量子系统;2)初始化,即量子模拟器可以把系统制备在一个确定的态上,理想情况下,应该是纯态;3)设计,即可以设计一系列的与外场或者不同粒子之间的可控制的相互作用;4)探测,可以对量子模拟器进行测量;5)验证,超导量子电路是一个多自由度的介观量子系统,因为约瑟夫森结的非线性特征,超导量子电路可以视为具有非均匀能级结构(即可调控)的人工原子.超导量子电路工作于极低温度(mK级)环境,因此只要等待时间足够长(约几倍能量弛豫时间),人工原子就能弛豫到基态,实现初态制备.超导量子电路系统可以通过使用微波谐振腔和超导量子比特(即人工原子)实现强耦合,此外超导量子比特不但可以实现单次的破坏性测量,也可以进行量子非破坏性测量.因此,超导电路系统是很好的量子模拟器.
3 基于超导电路系统对拓扑体系的量子模拟
3.1 基本原理
一般而言,在立方晶格的基础上,通过紧束缚近似构造两能带模型可以描述某些具有拓扑相的凝聚态物质系统,这个模型的一个典型哈密顿量(自旋−1/2)在准动量空间(即K空间)中可以描述为

其中σi(i=1,2,3)为Pauli矩阵.
利用旋转波近似,在以驱动微波频率旋转的旋转坐标系中,与微波光子相互作用的二能级系统的哈密顿量可化为

其中Ω1,Ω2分别是沿x轴、y轴的Rabi频率,Ω3=ω21−ωm是系统能级间隔(即跃迁频率)与微波频率之间的失谐.Ω1,Ω2由驱动微波的振幅、相位决定,Ω3由驱动微波的频率决定.
通常情况下,K各分量之间对易并且和哈密顿量对易,我们可以把di(i=1,2,3)看作参数而不是算符.因此通过校准参量Ω1,Ω2,Ω3,利用微波有源器件,设计微波振幅、频率和相位,使Ω1=Ω∗d1(K),Ω2= Ω∗d2(K),Ω3= Ω∗d3(K)(Ω 为能量单位),可以将拓扑体系的准动量空间(K空间)精确映射至超导量子电路的微波场参数空间(Ω空间),即可实现H(K)的精确模拟.通过连续调整微波场参数,测量不同参数下的量子比特能谱,可以直接得到晶格在第一布里渊区的能带结构,在此基础上可以进一步研究其拓扑性质.该方法可以进一步推广至高自旋体系,对应于三能级乃至多能级系统.
3.2 实验方案
下面以超导传输子量子比特(以下简称Transmon)为例来说明基于超导量子电路的拓扑能带模拟方法.
超导电路系统中量子调控和量子读取装置如图2所示[11].样品放置于稀释制冷机中,并冷却至10 mK左右的基本温度.3D Transmon系统的动力学等价于人工原子与谐振腔耦合,由电路量子电动力学描述[12].在3D腔上有两个SMA接头,分别用于微波输入和输出.调控和读取qubit的微波脉冲在合适的衰减和滤波后,通过输入接头送入.用于驱动量子比特的微波需要精确调节相位以达到操纵量子比特的目的,通常利用任意波形发生器(arbitrarywaveformgenerator,AWG)和双臂混频器(inphase and quadrature mixer,IQ mixer)联合实现驱动微波的开关和相位调制.为了读出qubit的状态,一般应设计微波外差装置[13].输出微波由位于稀释制冷机中4K平台的高电子迁移率晶体管(high electron mobility transistor,HEMT)预放大,并且在室温下由两个低噪音放大器进一步放大,然后利用外差装置,把微波信号转换为中频信号,并被数据采集卡(data acquisition card,DAQ)采集.
考虑到实验的主要目标是测量能谱,一般选择高功率读取(high power readout)方案[14],这样不仅能够有效增强数据的信噪比,而且可以简化实验步骤和数据分析.所谓高功率读取方法,简单来说就是送入一个与腔模共振的微波,由于高功率下谐振腔的非线性性,微波的传输振幅将反映Transmon状态.

图2 3D超导Transmon比特的调控与读取实验装置图 红色线框中的微波源联合IQ mixer用于调控qubit,蓝色线框中的微波源通过谐振腔的传输特性读取qubit状态,绿色线框表示利用微波外差装置收集数据,室温放大器用于增强信噪比Fig.2.Schematic of experimental setup for a 3D superconducting transmon qubit.The microwave source in red box combined with IQ mixer is used to manipulate qubit.Another microwave source in blue box is used to read out qubit state by measuring cavity transmission.Digital heterodyne is used for data acquisition.Transmission signal of cavity is mixed down to 50 MHz by arbitrary waveform generator and IQ mixer.Amplifiers are used to increase signal-to-noise ratio.
根据电路量子电动力学理论,Transmon与谐振腔的耦合体系是非谐性多能级体系,在实验中,通常可以使用最低的三个能级|0,|1,|2,状态|1,|2构成自旋1/2的人工原子,与微波场的耦合可以用三个泡利矩阵σ1,σ2,σ3描述,从而构造哈密顿量.|0态被选作为辅助能级,可以把系统初始化到该能级,用于探测该模拟系统的能谱.在能级|1,|2之间加入驱动微波,两个能级将与微波场耦合,忽略|0态影响,系统由哈密顿量(2)描述,本征能量为±}Ω,考虑|0态影响,两个能级将与微波场耦合产生奥特勒-汤尼斯劈裂(Autler-Townes splitting)[15],从|0态到|1态的跃迁将变为从|0态到劈裂后的缀饰态的跃迁,此时在能谱上将观测到相近的两个共振峰.缀饰态的本征值大小为±}Ω/2,相应的劈裂大小为}Ω.因此通过控制微波,将能够测量某些拓扑材料第一布里渊区的能带结构.
拓扑材料的拓扑性质主要包括拓扑保护和拓扑相变.拓扑保护主要依赖于哈密顿量的对称性,在哈密顿量中引入破坏或保护对称性的微扰,依上述方法测量其能带结构,观察能带交叉点的变化可分析拓扑保护性.拓扑相变由拓扑不变量表征,在改变系统的参数过程中,拓扑不变量的突变意味着拓扑相变的发生,拓扑材料的拓扑不变量一般和电子绝热的经历布里渊区所积累的Berry相位相关.最常见的拓扑不变量是Chern数,它等于基态电子的Berry曲率沿拓扑材料能带的布里渊区的曲面积分.表征拓扑不变量的测量方法主要有两种,一种方法是利用绝热方法测量Berry相位[16],另一种方法是利用动力学方法测量Berry曲率[17],并直接计算拓扑不变量.
绝热方法测量Berry相位的关键是消除动力学相位,根据动力学相位与演化路径无关,只依赖于瞬时本征能量对时间的累积,而几何相位与演化路径有关,且依赖人工原子的状态的特点,可以利用自旋回波π脉冲消除动力学相位.经过自旋回波量子比特|0和|1态发生反转,动力学相位将变成不具有观测效应的整体相位,几何相位则变成具有观测效应的相对相位.为简化实验,一般将量子比特的初态制备在|0到|1的叠加态,利用Ramsey干涉方法测量Berry相位,最后根据量子态层析的结果得到几何相位[18].动力学测量方法的原理与利用粒子在弯曲空间的运动轨迹推导空间曲率分布相似,以一定速率改变哈密顿量,即等效于在弯曲空间移动一个人工原子,贝里曲率将导致量子态在Bloch球上的运动轨迹偏离预定演化路径,根据动力学响应可测定基态电子的Berry曲率,测定能带各点的贝里曲率,通过曲面积分即可以计算出体系的拓扑不变量.由于动力学方法仅要求体系准绝热演化,因此比绝热方法更具普遍性.
4 自旋1/2系统的模拟
在实际拓扑材料中实现能谱测量,并研究拓扑相变等性质或合成理论预言的新型拓扑材料十分困难.目前,量子模拟是研究拓扑材料的一种重要的研究方案,研究者已经在多种可控量子系统中成功实现了对特定拓扑体系的模拟.清华大学段路明课题组在2017年和2018年分别以金刚石NV色心和冷原子系统为量子模拟器研究了Hopf绝缘体[19,20],他们通过模拟Hopf绝缘体的二能带模型哈密顿量,发现了编码在Hopf绝缘体自旋电子学中的链环或纽结结构,并分别基于离散化方案和time-of-flight成像技术进行能带基态的量子态层析测量,通过能带基态计算出相应的Berry曲率,得到描述该3D拓扑绝缘体的拓扑不变量,首次实现了早已由理论预言但却从未在实验上观测到的这一类拓扑材料的系统研究.
相比其他人工量子系统,超导量子电路系统的调控主要基于成熟的微波技术,因此单个量子比特的可控性更强,实验的测量精度也更高,同时超导量子比特的扩展性较好,最有希望实现多比特耦合体系.通过近几年的研究,我们课题组已经发展出一套基于超导电路系统模拟拓扑体系的研究方法,以下主要介绍利用超导电路系统模拟拓扑半金属的工作
拓扑半金属是一类全新的拓扑电子态,其能带结构的导带和价带在动量空间相交形成一系列能带交叉点,近年来已迅速成为量子材料领域的研究热点.根据能带在费米面附近的交叉点在晶格动量空间的分布,拓扑半金属一般可以分为Weyl半金属、Dirac半金属和节线半金属以及其他一些非常规的拓扑半金属.
4.1 时间-空间反演(P-T)对称性保护的拓扑半金属
众所周知,时间反演对称性(T),空间反演对称性(P),电荷共轭对称性(C)是粒子物理学重要的三类分立对称性,在凝聚态物质体系中,P,T,C对能带结构的约束也普遍存在,将导致关于能带结构的拓扑分类方法[21],在P,T,C的各种联合对称性中,PT联合对称性即时空反演对称性可以表示为:xµ→−xµ,其中µ=0,1,2,3.
一个具有代表性的描述受PT对称性保护的拓扑半金属(简称PT半金属)的哈密顿量(设为无量纲的)在准动量空间(即K空间)中可以写为[22]:


其中,σi(i=2,3)为泡利矩阵,λ为可调参数.
考虑哈密顿量的对称性,空间反演算子和时间反演算子可以表示为P=σ3i和T=Ki,其中i是K空间反演算子,K为复共轭算子.显然,该哈密顿量具有独立的时间反演对称性和空间反演对称性.因此,该哈密顿量也具有PT联合对称性,在能带理论中,PT对称性可以用对易关系[A,H]=0表示,其中H是系统哈密顿量,A=σ3K为反幺正算子,满足A2=I,根据群理论,可以预言此二维系统的能带结构在能带交叉点存在Z2拓扑电荷(拓扑量子数).当−1<λ<1时,上述模型描述一个二维的拓扑非平庸系统,有4个具有Z2拓扑电荷的能带交叉点.值得注意的是,尽管该简化模型具有独立的P,T对称性,能带交叉点的拓扑稳定性仅仅要求PT联合对称性.
利用超导量子电路的参数空间和晶格Hamilton量动量空间(K空间)的映射,通过微波场调控超导量子比特,得到哈密顿量(3).参数λ对PT半金属的拓扑性质起关键作用.为观测能带结构,不失一般性,可设λ=0,测量系统在第一布里渊区的完整能带,如图3所示.在实验中,对于第一布里渊区,即(kx,ky)∈ [−π,π)×[−π,π),通过测量微波吸收共振峰,便可确定共振峰频率作为kx,ky的函数.PT半金属的主要特点是反映能带交叉的非平庸Z2类型Dirac点,若观测到Dirac锥结构,即表明实验已经成功地模拟出PT半金属能带结构,如图3所示,Dirac点的位置在(π,±π/2),(0,±π/2),和λ=0的理论计算结果一致.
超导电路系统可用于研究受PT对称性拓扑保护的非平庸Z2类型Dirac点的拓扑稳定性.为此在实验中引入微扰=ησ2(η=1/2Ω为常数),此时哈密顿量(3)中σ2项的系数为Ω2(kx)=Ω(sinkx+1/2),该微扰在破坏独立的P,T对称性的同时,依然保持PT联合对称性.系统能谱结构如图4(a)所示,可以发现,尽管能带交叉点的位置和能带图案发生剧烈变化,能隙依然没有打开.实验结果与拓扑能带理论预言一致.另一方面,引入另一微扰=εσ1(ε∼0.5Ω为常数),由于该微扰破坏了P对称性,保持了T对称性,因此在此微扰下,PT联合对称性遭到破坏,相应的,PT对称性的拓扑保护消失.实验结果如图4(b)所示,与理论预言一致,可以观察到此时能隙打开,一个平庸的绝缘相出现.

图3 典型的PT半金属能带结构图[23] (a)通过逐渐调节驱动微波的振幅、频率、相位,逐点绘制出系统在动量空间的三维能带结构;(b)通过将第一布里渊区的能谱作为kx和ky的函数可以得到能隙量级,可以清楚地在(0,±π/2),(π,±π/2)处观测到四个非平庸的Z2类型Dirac点,与理论预言一致Fig.3.Measured energy spectrum of a typical space-time inversion invariant topological semimetal[23]:(a)Three dimensional plot of the band structure of spectroscopy measurement,by tuning the driving amplitude,frequency,and phase gradually,we image the band structure of the system in the momentum space point by point;(b)magnitude of energy gap obtained from direct measurements of the energy spectrum of the system as function of kxand kyin the first BZ,four nontrivial Z2-type Dirac points located inside the bright regions can be observed at(0,±π/2),(π,±π/2),in a full agreement with the theoretical prediction.
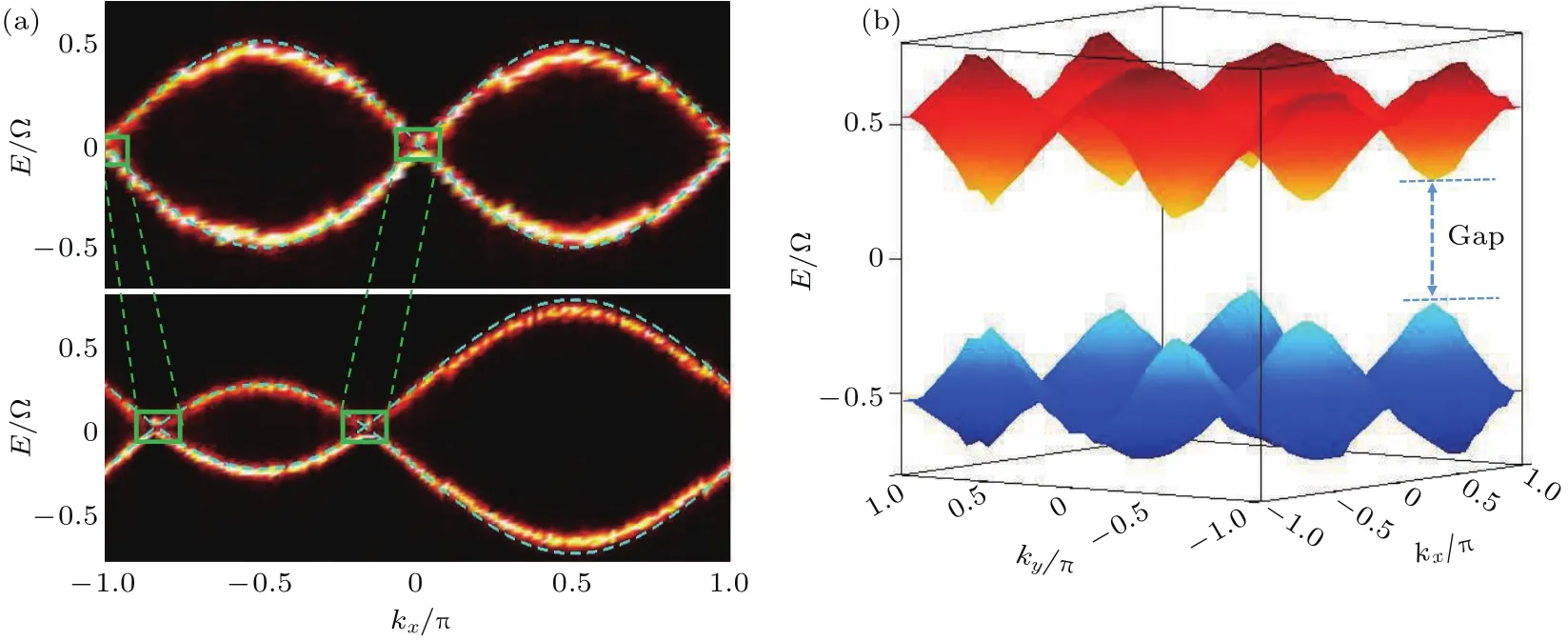
图4 在两种具有代表性的微扰作用下研究Dirac点的拓扑性质[23] (a)当引入破坏独立的P,T对称性,但保持PT联合对称性的微扰=ησ2后,Dirac点依然存在,虽然此时能带交叉点的位置和能带图案发生剧烈变化,这表明Dirac点的拓扑性质受PT联合对称性保护,其中,上下两图位于ky=π/2平面,参数η分别为0和0.5,黄线和绿线分别表示实验数据与理论结果;(b)当引入破坏PT联合对称的微扰=εσ1后能带结构的变化,此时能带交叉点消失,能隙打开,出现平庸绝缘相,其中参数ε=0.5;(a),(b)中λ均取为0Fig.4.Symmetry-related topological features of the Dirac points for two different but representative kinds of perturbations.(a)When=ησ2is added with η=0.5 in unit of Ω,which breaks both T and P but preserves the PT symmetry,Dirac-like points still exist,though the gapless point positions are shifted(marked by the green square)and the band pattern is distorted drastically,showing the robust of the topological nature protected by the PT symmetry.Top and bottom panels correspond respectively to the cases of η =0 and η =0.5 on the plane of ky=π/2.The bright yellow and dashed green lines denote the experimental data and theoretical calculations from Eq.(3)with being added,respectively.(b)Whenever the PT symmetry is broken by adding the term =εσ1 with a constant ε (=0.5 Ω),a gap is fully opened.Here λ =0 for both(a)and(b).

图5 通过改变参数λ研究从拓扑半金属到绝缘体的拓扑相变[23] (a)λ分别对于0,0.5,1,1.5时kx≈0平面能带结构,可以观察到λ从到1再到大于1,Dirac点数目由4变为2在变为0,表明系统能隙逐渐打开,发生从拓扑半金属到绝缘体的拓扑相变;(b)第一布里渊区的最小能隙量级随参数λ的变化,与理论预言一致Fig.5.Quantum phase transitions from a topological gapless semimetal to a gapped insulator as changing parameter λ[23].(a)Spectroscopy at kx ≈ 0 for various λ.From right to left λ are 0,0.5,1.0 and 1.5,respectively.It is seen that when λ is increased from 0 to 1,then larger than 1,the number of Dirac-like points decreases from 4,to 2,then to 0,where the gap gradually is opened,demonstrating that a topological PT invariant semimetal phase transits to a normal insulator phase.(b)magnitude of minimum energy gap in the first Brillouin zone as a function of λ,as predicted theoretically.
利用超导电路系统还可以考察拓扑电荷的Z2性质.对于一些具有代表性的λ值,能谱如图5所示,可以观察到Z2类型能带交叉点合并直至消失的过程.根据拓扑能带理论的一般性原理可知,即使保持PT对称性,两个能带交叉点νZ2=1合并成一个平庸拓扑电荷的能带交叉点νZ2=2≡0 mod 2,也将使能隙打开.如图5(a)所示,实验中从到2连续增加变量λ.在kx=0平面上,当λ=0时,两个能带交叉点分别在ky=±π/2,当λ平滑地增加,两个能带交叉点逐渐相互靠近(注意布里渊区具有周期性),然后,当λ=1,在布里渊区边界处两个能带交叉点合并为一个新的能带交叉点,根据拓扑能带理论,这是一个拓扑平庸点,当λ>1时,可以观察到具有平庸拓扑电荷的能带交叉点打开,拓扑半金属转变为平庸绝缘体,这验证了理论预言,如图5(b).
4.2 Hopf-link半金属
除了具有能量节点的能带结构,人们还理论预言了具有能量节线的拓扑能带结构.这些节线还可以形成链状结构,比如Hopf-link.一个典型的描述Hopf-link半金属的哈密顿量(设为无量纲的)在准动量空间(即K空间)中可以描述为[24]:
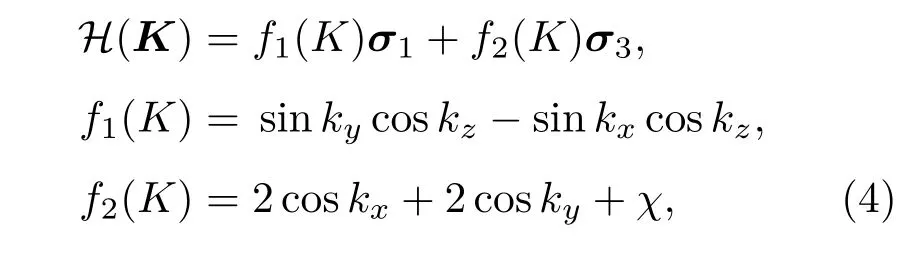
其中σi(i=1,3)为泡利矩阵,χ为可调参数.
由哈密顿量(4)可知,两个曲面Sx:f1(K)=0和Sy:f2(K)=0在布里渊区内相交形成两条节线,并且两条节线成双螺旋结构,考虑到布里渊区的周期性,如图1所示,双螺旋结构投影,即导带和价带接触点构成一个Hopf链[24](如图6(a)所示).
考虑哈密顿量(4)的对称性,对于一个没有自旋轨道耦合的系统,时间反演算子作用于哈密顿量(4)得TH(K)T−1=H∗(−K),空间反演算子作用于哈密顿量(4)得PH(K)P−1=H(−K),即独立的时间反演对称性和空间反演对称性都是破缺的;而考虑PT联合对称性,得[H(K),PT]=0,即这个相也受到PT联合对称性的拓扑保护[24].
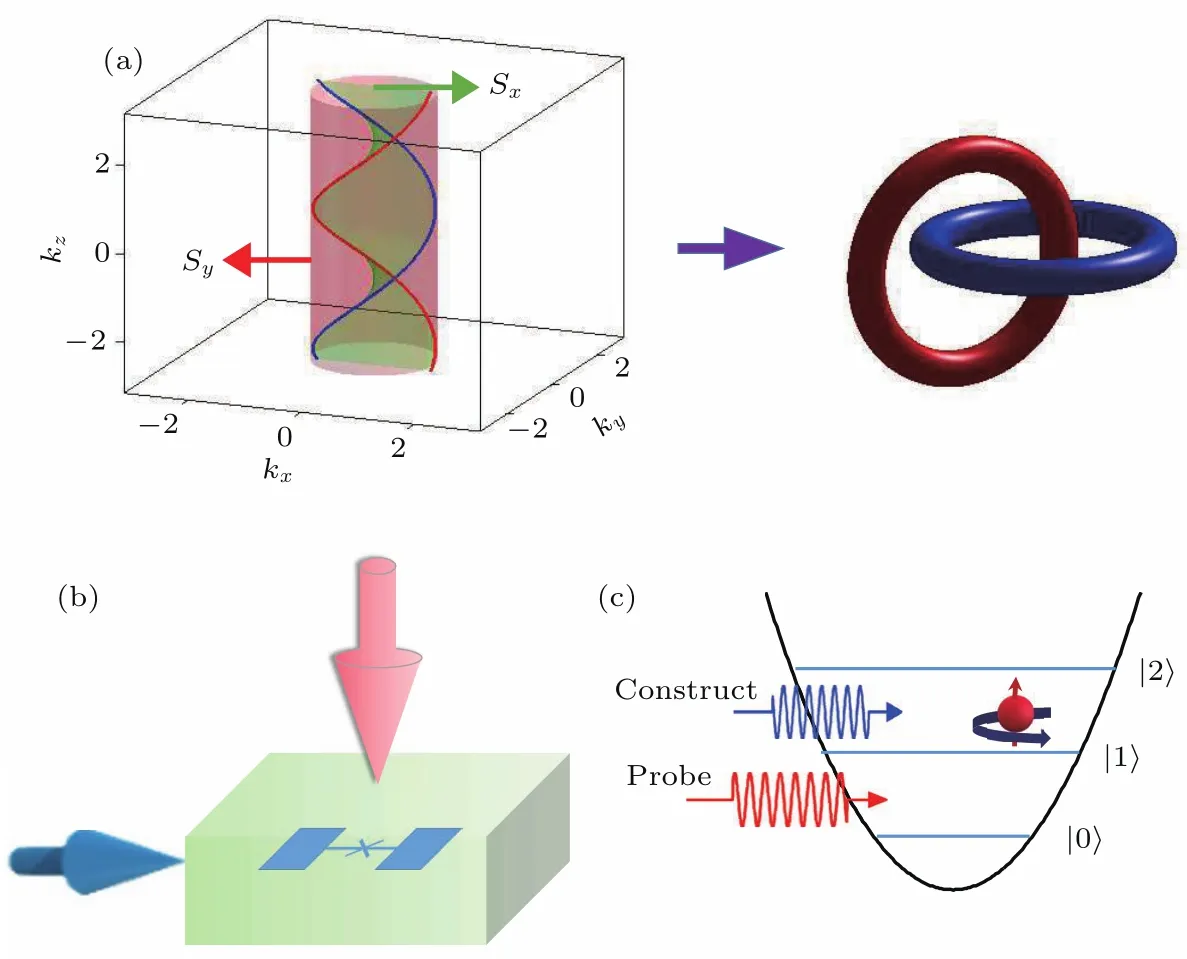
图6 实验方案[26] (a)曲面Sx和Sy在布里渊区内相交形成与Hopf链拓扑等价的两条双螺旋结构节线;(b)实验上用于模拟Hopf-link半金属有效哈密顿量的3D Transmon样品;(c)Transmon的能级结构图解,最低的三个能级用于量子模拟Fig.6.(a)Nodal lines with a double-helix structure formed by the intersection of two surface Sx and Sy,it is topologically equivalent to a Hopf-link;(b)a superconducting transmon embedded in three-dimensional cavity are driven by designed microwaves,realizing the effective Hamiltonian to simulate Hopf-link semimetals;(c)the schematic energy structure of a transmon,the lowest three energy levels are used to do the simulation[26].
理论预言参数χ对拓扑半金属的双螺旋节线的形成起重要作用[27],因此首先可以利用超导电路系统测量随着χ的变化,Hopf-link半金属能带结构的变化.采用前面提到的实验方案,系统初始状态设定处于|0态,预先设置参数范围为第一布里渊区,即(kx,ky,kz)∈ [−π,π)×[−π,π)×[−π,π),逐渐改变kx,ky,kz的值,从共振峰能谱可得到半金属在第一布里渊区的完整能带.能带结构节点即能量零点能够从能带中直接得到.如图7所示,不难发现第一布里渊区的节点可以形成一条节线.当χ=−3时,能够观测到双螺旋结构,且节线位置与理论计算结果符合得很好,这表明该方案成功实现了Hopf-link半金属的能带模拟.随着χ的增加,曲面Sy扩张,导致双螺旋结构发生剧烈改变,在χ=0时,Sy接触布里渊区边界,双螺旋结构畸变,在χ=2时,Sy形成一个中心位于(π,π)的圆柱,曲面Sx,Sy的交集依然保持双螺旋结构.
与PT半金属情形相似,利用超导电路系统的可调控性也能够探究Hopf-link半金属的拓扑相变和拓扑稳定性.首先可以引入一个附加项=λsinkyσ1来研究link-unlink拓扑相变,其中以Ω为单位,λ为可调参数,图8(a)所示为λ依次为不同值时半金属的节线结构,当λ<1时,两条节线相互连接,逐渐增加至λ>1,两条节线分离,形成两个拓扑不连接的孤立圆环,对于λ=1,节线相交于一点,可以认为该点即为拓扑相变的临界点.考虑到哈密顿量(4)与PT对易,Hopf-link半金属应当受PT联合对称性保护,为了验证这一点,可在哈密顿量(4)中添加一项微扰=ησ3,其中以Ω为单位.此时哈密顿量(4)的P,T对称性均被破坏,但是保持PT联合对称性,实验表明随着η的增加,能带结构逐渐扭曲,并且位于布里渊区的节线位置逐渐变化.然而,节线依然形成双螺旋结构,没有打开能隙,如图8(b),这支持Hopf-link结构受PT联合对称性的拓扑保护的理论.
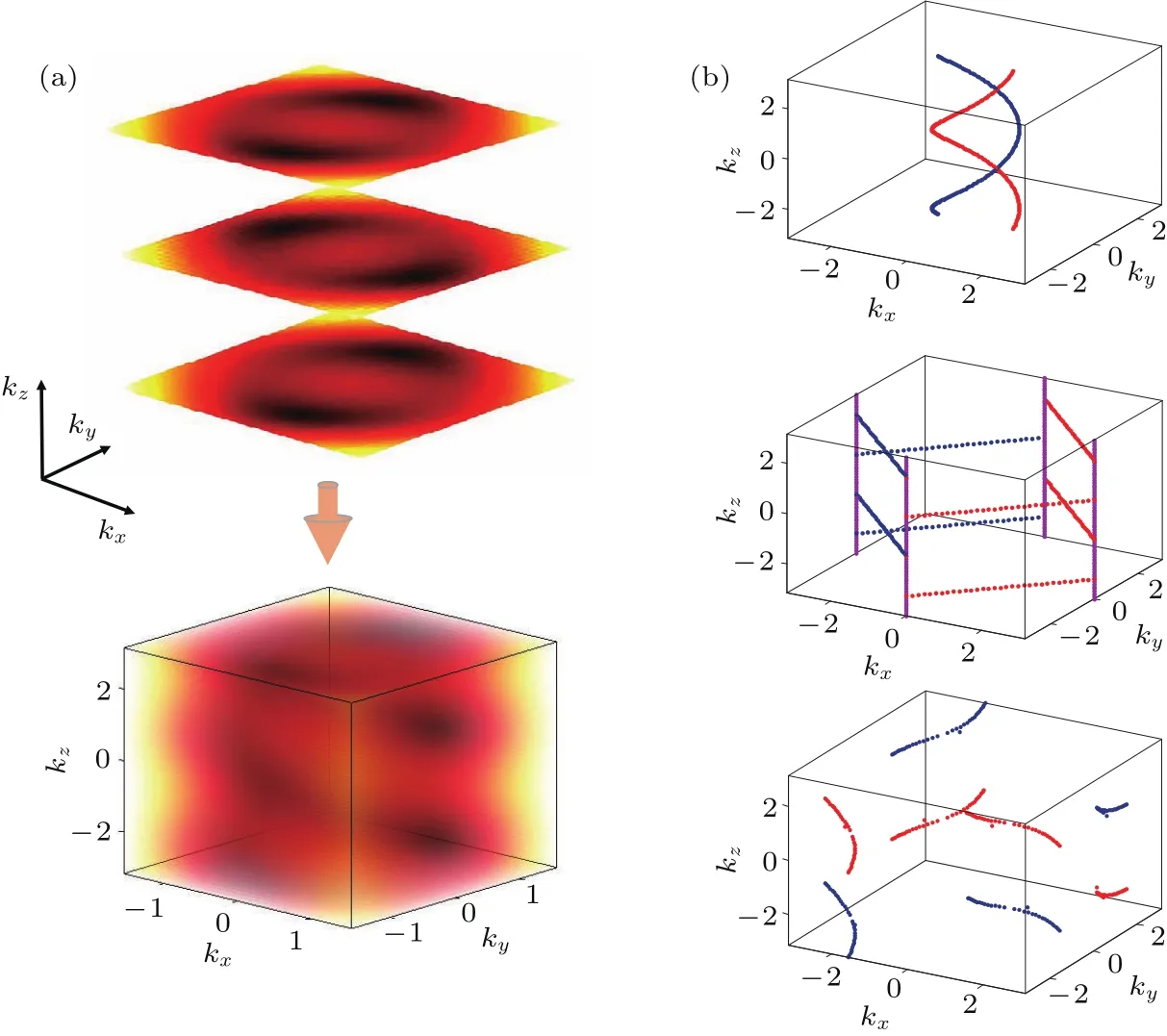
图7 Hopf-link半金属在第一布里渊区的能带结构[26] (a)上图表示在区间[−π,π]内逐步变化kz得到的等能线,下图表示综合等能线得到Hopf-link半金属的节线,为了清晰地绘制无限能带结构,可以选定(kx,ky)测量范围为[−π/2,π/2)×[−π/2,π/2);(b)从上到下参数χ分别等于−3,0,2时的节线Fig.7.(a)Measurement of the band structure of the Hopf-link semimetal in the first Brillouin zone.Top panel:contour plots of the energy gap with varying kzgradually in the range of[−π,π].Bottom panel:By collecting all these contour plots together,we obtain the nodal lines of the Hopf-link semimetal.To image the gapless band structure clearly,we set the range of(kx,ky)as[−π/2,π/2)×[−π/2,π/2).(b)Nodal lines obtained from the measured energy spectrum for various χ.From top to bottom:χ=−3,0,and 2,respectively[26].
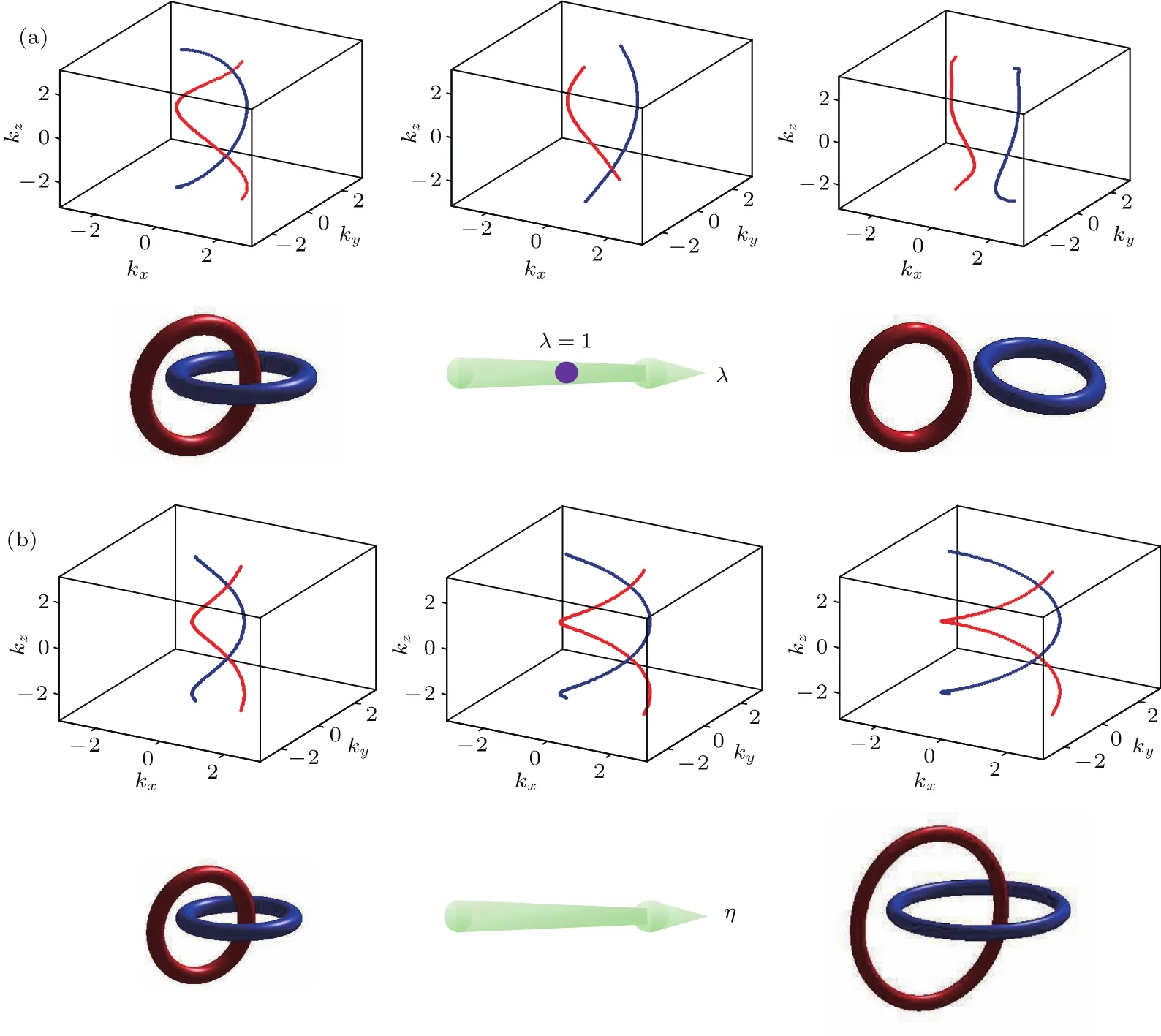
图8 两种具有代表性的微扰作用下节线的拓扑性质[26](a)引入微扰=λsinkyσ1后,Hopf-link半金属的link-unlink相变,从左到右分别为参数λ=0.5,1.0,1.5时的节线位置,正如理论预言,λ=1为临界点,此时两条节线仅相交一点;(b)引入微扰=ησ3时,Hopf-link半金属的拓扑稳定性,从左到右分别为参数η=−0.5,0.5,1.5时的节线位置Fig.8.(a)Link-unlink transition of the Hopf-link semimetal after we added =λsinkyσ1to the Hamiltonian(4).From left to right:nodal lines with λ =0.5,1.0,and 1.5,respectively.As predicted,λ =1 is the critical point,where two nodal rings only touch at one point.(b)Stability of the Hopf-link against the perturbation of=ησ3.From left to right:nodal lines with η = −0.5,0.5,and 1.5,respectively[26].
拓扑不变量是一个与拓扑现象紧密相关的特征量.描述Hopf链拓扑性质的拓扑示性数为连环数.理论上通过测量系统沿参数空间的封闭路径绝热演化积累的Berry相位可以得到连环数的信息[25].通过绝热方法在超导电路中测量Berry相位是一种十分方便的方法[28,29].
如图9(a)所示,对于具体的实验,我们需要在布里渊区内设计一条穿过Hopf链的封闭路径以测量Berry相位,此时整个绝热演化过程由两部分构成,由紫色虚线标志的部分,穿过Hopf链,贡献了Berry相位π,由灰色虚线标志的部分,对Berry相位没有贡献.在实验设计上,必须将动量空间的回路映射到超导电路系统的参数空间.理论上,由紫色虚线标志的回路与Bloch球面上经线等价,不失一般性,可以设计一条测地线以取代原始路径,测地线选取{Ωx,Ωy,Ωz}={sinθcosϕ+Λ1,Λ2sinϕ,cosθcosϕ+Λ1}其中θ∈[0,π],ϕ∈[0,2π]为球面坐标.通过调整参量Λ1和Λ2,即可在布里渊区构造任何封闭路径.这里我们利用Ramsey干涉技术,测量绝热演化后的Berry相位.通过调整参数,可以移动K空间封闭路径的位置.如图9(d)所示,在kz=0平面沿kx轴移动紫色虚线的位置,原本环绕红色节线的回路不再环绕任何节线,测得的几何相位在kx=π/3突然由π变为0,这表明在这个临界点,参数空间的封闭路径不再是测地线.同时,通过在kx=0平面沿kz轴移动回路,原本环绕红色节线的回路开始环绕蓝色节线,在kz=π/2时Berry相位突然由π跃变至−π.综上,在第一布里渊区测量的Berry相位很好地描述了Hopf链的拓扑性质.

图9 构造闭合回路测量Berry相位[26] (a)在第一布里渊区内沿一条封闭路径(虚线)测量积累的Berry相位的实验方案;(b)量子比特在与(a)中准动量空间相对应的参数空间中的演化路径;(c)测量量子比特沿(b)中所示路径演化而积累的Berry相位的时序方案;(d)Berry相位对演化路径的依赖性,实验测量了三个典型的Berry相位值:π,−π和0;(e)Berry相位分别作为kx(上图)和kz(下图)的函数Fig.9.(a)Schematic of an example of closed path(dashed line)in the first Brillouin zone to accumulate Berry phase,from which the linking number can be characterized;(b)evolving path in parameter space of qubit mapped from momentum space in(a);(c)schematic of time profile to probe Berry phase accumulated from the evolution in(b);(d)dependance of the Berry phase carried on the loop of the closed path,there are three typical values:π,−π and 0;(e)berry phase measured as a function of kx(top panel)and kz(down panel),respectively[26].
5 自旋为1的系统:Maxwell金属
利用超导量子电路还可以模拟一些高自旋系统.例如,最近新奇的费米型元激发引起了研究者的广泛兴趣,理论预言,在一些三重或多重简并点的能带结构中将出现不同于Dirac费米子或Weyl费米子的新型费米子——整数赝自旋费米子[30].
一个具有代表性的描述赝自旋-1自由费米子的哈密顿量(设为无量纲的)在准动量空间(即K空间)中可以描述为[31]:
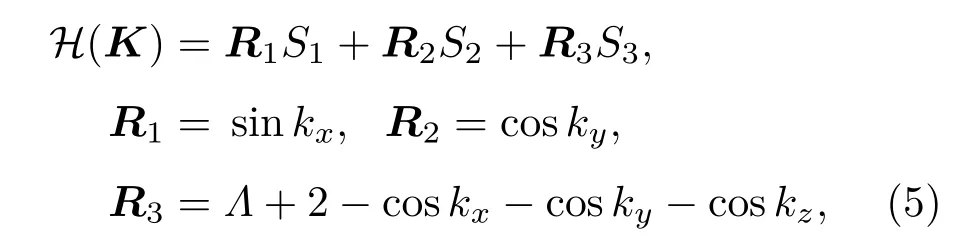
其中K=(kx,ky,kz)表示准动量,Λ为可控参量,Ri(i=1,2,3)为自旋-1矩阵.
对于上述模型的哈密顿量,选择合适的Λ,在第一布里渊区存在三个能带,其中能量为零的平带(flat band)位于另外两个能带中间.在某些点三个能带相互接触,形成三重简并点.例如,当|Λ|<1,能带有两个三重简并点在M±=(0,0,±arccosΛ)处,在M±附近有效哈密顿量为H±(q)=q1S1+q2S2±αq3S3,其中,该方程与描述光子的动量空间Maxwell方程相似,因此低能赝自旋-1元激发可由动量空间Maxwell方程有效描述[31,32].在这个意义上,类似于赝自旋-1/2系统的Dirac点和Weyl点,三重简并点称为Maxwell点.
由上述哈密顿量描述的自旋-1系统存在由Λ决定的两个不同的拓扑相,当|Λ|<1,系统能带中具有一对Maxwell点,即处于Maxwell金属相,当|Λ|>1,系统能隙打开,即处于拓扑平庸的绝缘相,在临界点|Λ|=1,两个Maxwell点合并,然后在能带中心处消失,表明此时系统发生了拓扑相变.相图和典型的能带结构如图10所示.
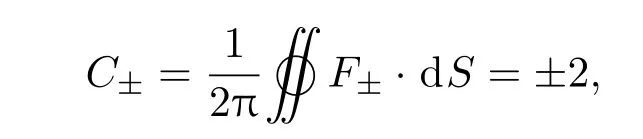
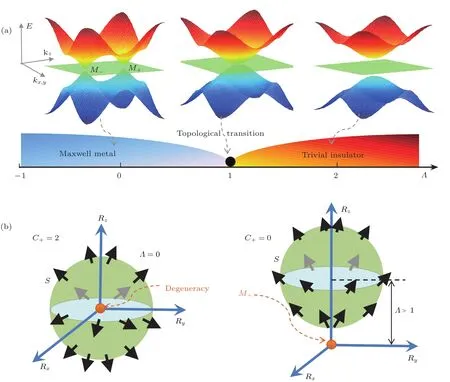
图10 赝自旋-1元激发系统的相图及拓扑直观解释[33] (a)赝自旋-1元激发系统关于参数Λ的相图,从左到右:当|Λ|=0时,系统处于Maxwell金属相,此时能谱出现一对Maxwell点;当Λ=1,系统发生拓扑相变,此时两个Maxwell点合并:当Λ=2,系统处于拓扑平庸的绝缘相,此时能隙打开,Maxwell点消失;(b)金属相与绝缘相拓扑性质差异的几何直观解释,当球面流形S沿z方向退化Λ距离,Berry流矢量在拓扑非平庸与拓扑平庸相具有本质的不同,当Λ=0(Λ>1),Berry流矢量完全(不完全)缠绕球面,二者分别给出Chern数C+=2(C+=0)Fig.10.Phase diagram and geometric illustration of the spin-1 Maxwell system[33].(a)Phase diagram of the Maxwell system with respect to the parameter Λ.From left to right:the energy spectra for the Maxwell metal phase with a pair of Maxwell points denoted by M±(Λ =0),the topological transition point with the merging of the two points(Λ =1),and the trivial insulator phase with band gaps(Λ =2);(b)geometric illustrations of the topological difference between the two distinct phases when the spherical manifold S moves from the degeneracy in the z direction by distance Λ.The Berry flux vectors are schematically presented by arrows,showing the different signature textures for the topological and trivial phases:the vectors fully(do not)wind around in the topological(trivial)case with Λ =0(Λ >1),giving the Chern number C+=2(C+=0).
也可以从拓扑不变量角度分析Maxwell金属.根据微分几何,描述Maxwell点M±的拓扑示性数是Chern数,Chern数可以用动量空间中封闭流形S上的面积分表示:其中F±表示Berry曲率.因此,拓扑相变可以由半径为1的球面流形沿z方向退化的距离Λ的运动表示.如图10(b)所示当|Λ|<1,系统处于具有非平庸拓扑电荷的Maxwell金属相,Chern数C±=±2,当|Λ|>1,系统处于具有平庸拓扑电荷的绝缘相,Chern数C±=0.
利用超导量子电路加上微波驱动,可以对Maxwell金属进行精确模拟.与自旋1/2系统不同,由于哈密顿量H(K)=R1S1+R2S2+R3S3,因此需要利用一个三能级系统模拟哈密顿量.由于超导量子电路是一个多能级系统,该实验需要选取能量最低的四个能态,记为其中|0作为辅助能态,与微波场耦合,构建需要模拟的哈密顿量.不失一般性,为了方便,在模拟中可以设ky=0.先将系统初始化在|0态,在给定kx和kz的驱动微波下,系统的本征态为|0d和一个探测微波脉冲将系统从|0态抽运到本征态,通过测量微波吸收共振峰,即可得到能谱.改变kx和kz,可以得到不同能谱,将能谱作为kx和kz的函数,即得到该拓扑体系在第一布里渊区的完整能带结构,如图11所示.与图10的理论结果一致,赝自旋-1的Maxwell系统的拓扑性质依赖于Λ.如图11(a)—(c)所示,通过实验可以测量具有代表性的Λ值的能谱.对于Λ=0,系统处于Maxwell金属相,位于(0,±π/2)的一对Maxwell点在kx-kz平面被观测到;当Λ增加到1时,两个Maxwell点合并,表明发生了拓扑相变;随着Λ进一步增加,Maxwell点在能带中心消失,系统变为平庸绝缘体.通过包含Maxwell点的横截面kx=0的E-kz平面,可以更清晰地观测到相变,如图11(d)—(f)所示.能谱的共振峰可以直接得到本征能量E±,正如理论预言,当Λ=1时,色散关系从平带的Maxwell点附近的线性关系变为平方关系.

图11 实验所测能带结构[33] (a),(b),(c)表示参数Λ=0,1,2时系统在第一布里渊区的完整能带结构;(d),(e),(f)表示参数Λ=0,1,2时系统在包含Maxwell点的横截面kx≈0的E-kz平面的能带结构;在Maxwell金属相可以观测到线性色散关系,理论计算结果用红色虚线表示Fig.11.Measured Maxwell bands[33]:(a),(b),(c)are band structures in the first Brillouin zone for Λ=0,1,2,respectively;(d),(e),(f)show the corresponding cross sections of band structures containing Maxwell points in E-kz(kx≈0)plane of(a)to(c).A linear dispersion is observed in the Maxwell metal phase.The theoretical calculations are plotted with the red dashed lines.
将测量自旋-1/2系统的Berry曲率的动力学方法推广至自旋-1系统[34],可以测量Maxwell点的Chern数.因为辅助能级在这个测量中不再需要,因此只需选取超导Transmon中最低的三个能级,分别记为|1,|2,|3. 在参数空间球面流形上需要设计一条包围Maxwell点M±的闭合回路.不失一般性,实验中可以选择{Ω12,Ω13,Ω23}={sinθcosϕ,sinθsinϕ,cosθ+ Λ},其中θ∈ [0,π],ϕ ∈[0,2π]为球面坐标,通过制备初始三能级态即S3的本征态,使演化路径起点位于北极点.然后,倾斜角度θ使系统沿子午线ϕ=0准绝热演化.最后,在某一时间tmeasure停止准绝热演化,并对此三能级系统实行层析.对任意tmeasure,我们可以通过测量⟨S2的值计算Berry曲率,当Λ =0时,实验测得对于Maxwell点M±,Chern数分别为C+=1.98±0.34,C−=−2.14±0.05.
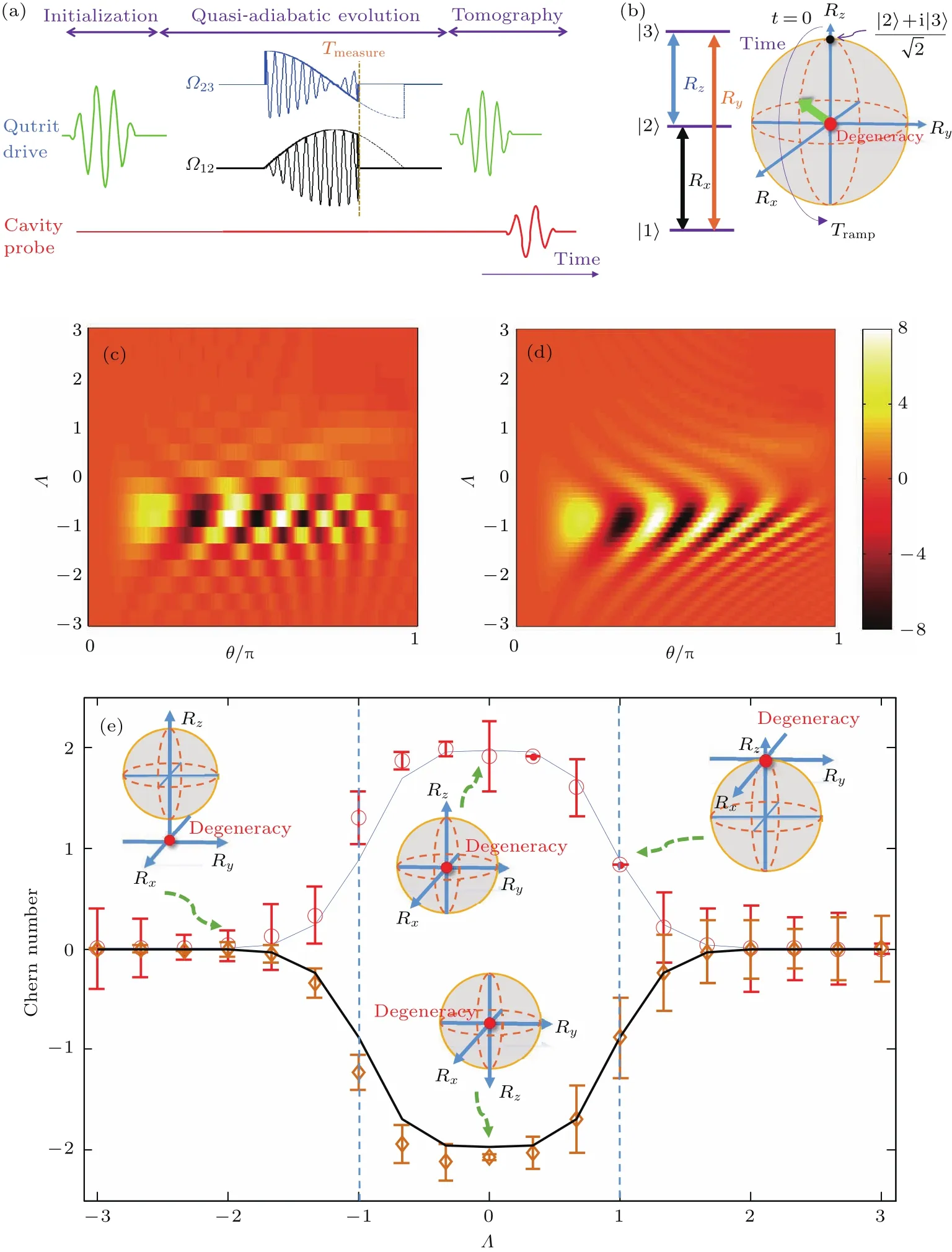
图12 测量Maxwell点的Chern数[33](a)表示测量Chern数的微波时序三态原子(qutrit)初始态位于(|2⟩+i|3⟩)驱动微波使原子沿子午线做准绝热演化,经过时间tmeasure后对末态做层析;(b)三个最低能级耦合微波用于构建赝自旋-1系统的哈密顿量,设计微波时序使系统在参数空间的球面流形上沿子午线ϕ=0演化;(c),(d)表示测量得到的作为θ和Λ的函数的Berry曲率振荡图案表示非绝热响应;(e)表示测量得到的作为参数Λ的函数的Chern数,当|Λ|<1时,|C±|≈2表明系统具有非平庸拓扑电荷,即系统处于Maxwell金属相;当|Λ|>1时,|C±|≈0,表明系统具有平庸拓扑电荷,即系统处于绝缘相 √Fig.12.(a)Time profile for the measurement of Chern number.The qutrit state is initialized at(|2⟩+i|3⟩)/2 and then evolves quasi-adiabatically during a non-adiabatic ramp,which is followed by state tomography;(b)three lowest energy levels{|1⟩,|2⟩,|3⟩}coupled by pluses Rx,y,zare used to construct the spin-1 Hamiltonian,and the pulse sequence results in a parameter-space motion along the ϕ=0 meridian on thespherical manifold;(c)and(d)The measured and simulated(with the measured decoherence time of the transmon)Berry curvature as functions of θ and Λ.The oscillation pattern suggests a non-adiabatic response;(e)the measured(circles and diamonds)and simulated(solid line)Chern numbers as a function of Λ for the Maxwell points.For|Λ|<1,|C±|=2 indicates the Maxwell points in the topological Maxwell metal phase;for|Λ|>1,|C±|=0 indicates the system in the trivial insulator phase[33].
为了进一步理解拓扑相变,可以利用超导电路系统测量Maxwell点的作为θ和Λ的函数的Berry曲率.如图12所示,在Λ =0时,Chern数|C±|≈2,表明体系具有非平庸拓扑电荷,即处于拓扑非平庸相——Maxwell金属相.通过沿R3轴移动变化Λ,当|Λ|<1时,依然有|C±|≈2表明系统依然处于拓扑非平庸相,当|Λ|>1时,|C±|≈0,表明系统不具有非平庸拓扑电荷,故处于平庸绝缘体相.因此拓扑相变发生在|Λ|=1时,此时Chern数在两个分立值之间发生突变.值得注意的是,实验数据显示在临界点Chern数的转变不是突变式的,这主要是因为超导量子电路存在有限的退相干时间.
利用超导三能级系统可以帮助我们研究具有非常规的拓扑能带结构凝聚态物质——Maxwell金属的拓扑性质.事实上,利用上述模型,还可以进一步模拟赝自旋-1粒子的相对论粒子动力学.同时,通过充分利用超导人工原子的更多能级,可以模拟具有更高自旋量子数元激发的拓扑体系的能带.
6 总结与展望
本文主要介绍了利用单比特超导电路系统对拓扑材料能带结构的模拟,在此基础上研究了拓扑体系的物理性质,如拓扑保护、拓扑相变、拓扑不变量等.鉴于在实际材料中研究拓扑性质的困难,上述实验结果表明基于超导电路系统的量子模拟器作为一个强大的工具有助于对拓扑体系更深入的研究,为研究拓扑体系的物理性质提供了一种独特的思路.当然,耦合多比特系统是目前研究的重要方向,它可以在模拟更复杂的拓扑体系方面发挥重要作用.比如UCSB的研究团队利用两比特超导电路系统成功地模拟出描述拓扑系统的重要模型——Haldane模型[35].但是由于多比特体系难以实现精确调控,目前国际上利用超导电路系统进行拓扑量子模拟主要仍是基于少数量子比特体系实现的.但利用多比特模拟更加复杂的甚至具有相互作用的凝聚态系统仍然是以后发展的重要方向.可以预见,随着模拟方案的优化和调控技术手段的提高,利用多比特体系研究拓扑材料的实验方法也将日趋成熟,拓扑量子模拟这个方向将会不断发展.
