单分子尺度的光量子态调控与单分子电致发光研究∗
2018-12-18张尧张杨董振超
张尧 张杨 董振超
(中国科学技术大学,合肥微尺度物质科学国家研究中心,合肥 230026)
(2018年9月16日收到;2018年10月26日收到修改稿)
1 引 言
未来信息和能源技术的一个重要发展方向是基于分子和纳米结构的单分子光电器件的研究[1−3],其物理基础在于分子尺度上的光电相互作用规律.而可控地实现单分子电致发光是研究诸如单分子尺度的光电转化及分子与场的相互作用等规律的实验基础.从实现单分子电致发光这一目标所采用的器件构型上看,可以将目前的单分子电致发光研究主要分成两类:一类是基于微纳电极加工技术的横向型器件结构的研究,另一类是基于扫描隧穿显微技术(STM)的竖直型器件结构的研究.对于基于微纳电极加工技术的横向型器件结构的研究而言,这类技术非常有利于未来光电器件的集成.在这类研究中所使用的发光材料一般为单个的纳米粒子[3−5]、纳米线[6]、或纳米管[7,8],或纳米管和分子的复合体系[9].此类研究的难点在于将纳米管线等纳米结构可控地植入这种微纳电极之间本身就很难,而要将有机单分子清晰地定位于这种纳米隧道结、构成有效接触并实现可控发光的难度就更大了.而基于STM技术的竖直型器件结构,不仅可以利用扫描针尖本身特有的高空间分辨能力直接获得分子的实空间几何结构特征与电子态信息,而且其高度局域化的隧穿电子还可以用来激发分子,可以获得分子的局域光学响应信息,这使得它成为在空间和能量尺度上深入研究单分子发光特性的有力工具.因此,基于STM诱导发光技术(STML)的竖直型器件结构的研究[10],是目前研究有机单分子电致发光的主要手段[11−17].
要实现STM隧道结中的单个分子的电致荧光需要解决两个难点.其一,是如何避免金属性衬底对分子荧光的淬灭.由于STM研究中需要使用金属性的衬底,然而,对于直接吸附在金属衬底上的分子,由于存在与衬底间的直接电荷转移,处于激发态的分子会很快将能量传递给金属衬底,从而导致分子荧光被淬灭.因此,为了抑制荧光淬灭,常常需要采用物理[12−14,18−22]或化学[23,24]的脱耦合方法来隔绝分子与金属衬底间的直接电荷转移以及削弱分子与金属衬底间的能量转移.其二,由于单分子的电致发光强度非常弱,要有效探测到远场的荧光信号,还需要调控STM隧道结中的纳腔等离激元(NCP)共振,使之与分子本征能级间跃迁的能量相匹配,以便有效地增强分子发光的强度.值得一提的是,纳腔等离激元不仅在分子发光增强中起着重要作用,还可以与单分子发生相互作用,从而导致相应的电致荧光光谱特征发生变化[21,25−27].此外,如果吸附在衬底上的单分子之间存在相互作用,相应的STML的光谱特征也会与独立的单分子有明显不同,这些光谱上的变化信息也可以为阐明分子间的相互作用机理提供依据[14,15,28].
在本文中,我们以锌酞箐(ZnPc)分子为研究对象,综合阐述我们研究组近些年在单分子电致荧光以及单分子光量子态调控领域的相关研究进展[29].通过将电子脱耦合和纳腔等离激元增强这两种分子激发态调控技术有效结合起来,我们可以在单个中性ZnPc分子上获得强而稳定的单分子电致荧光.通过发展与STML技术相结合的光子符合计数(HBT)系统,我们首次展示了来自孤立单个分子的电致荧光的单光子发射统计特性[20].我们还利用STM操纵技术,可控地构筑了ZnPc分子二聚体结构,并研究了分子间偶极-偶极相干耦合作用的实空间特征[14].此外,利用隧穿电子在分子旁边直接激发纳腔等离激元而不是直接激发分子,通过研究光谱特征中Fano线型的演化,研究了分子与纳腔等离激元之间的相干相互作用的规律[21].以上这些研究成果表明,单分子电致荧光研究可以为在单光子和亚纳米尺度上探索单分子及其耦合体系的发光特性提供新的方法,并为研发基于分子体系的量子光源、捕光结构以及纳米光电器件等提供了重要的科学信息和依据.
2 单分子电致发光和单光子发射
单光子源一直是量子信息领域的核心研究领域,清晰可控的高密度单光子源阵列更是构建量子芯片器件和量子网络的关键.在众多的单量子发光体(包括半导体量子点、原子、分子、色心等)中,单分子体系由于其发光频率易于调控、谱线较窄、且发光行为具有高度的均一性而受到广泛的关注.另一方面,电泵单光子源还在纳米光电集成和相关量子器件方面具有潜在的应用前景.有人曾尝试利用有机发光二极管器件结构来研究电激励分子单光子发射现象[30],但其研究手段很难排除周围环境对单分子发光特性的影响.在之前的单分子体系的电泵单光子源研究中,由于受到实验技术和荧光淬灭效应的制约,一直难以实现从空间位置和形貌确定的单个分子产生强而稳定的单分子电致发光信号,基于单个清晰分子的电泵单光子发射行为一直有待展示和验证.为此,我们利用STML技术对这一目标进行了攻关.针对电泵单分子单光子源的展示需要强而稳定的单分子发光的需求,我们通过长期摸索,精心选择了合适的金属电极、脱耦合层和荧光分子材料,利用氯化钠薄膜的脱耦合作用和银金属构成的纳腔等离激元的增强效应,成功获得了来自孤立单个酞菁分子强而稳定的分子荧光,并进一步通过光子强度相关性测量,清晰明确地展示了的电泵单分子单光子发射现象.

图1 单个ZnPc分子的STM诱导电致发光示意图[20]NaCl作为脱耦合层把分子与金属衬底隔开,抑制荧光淬灭效应Fig.1.Schematic of STM induced luminescence from a single ZnPc molecule adsorbed on the Ag(100)surface,where the NaCl serves as a decoupling layer[20].
如图1所示,利用氯化钠(NaCl)薄膜来隔绝单个的ZnPc分子与Ag(100)衬底之间的直接电荷转移,以避免分子荧光被淬灭.图2(a)展示出了分别吸附在3层和4层NaCl上的单个孤立的ZnPc分子的STML光谱(分别用蓝色和红色谱线表示).发光光谱在∼1.9 eV附近均表现出尖锐的具有分子特征的发光峰,这与文献中报道的中性ZnPc分子的Q带跃迁相符合,这表明3和4层的NaCl薄膜具有良好的脱耦合效果,使我们得以实现单分子电致发光.同时,图2(a)中还给出了银表面上的纳腔等离激元的光谱(如黑色谱线所示).从光谱特征上看,可以发现等离激元共振频率与分子发光能量之间有较好的匹配,这样的纳腔等离激元模式可以较好地增强分子荧光并使我们可以观察到较强的单分子电致发光信号.图2(a)中展示的单分子发光是在−2.5 V的激发偏压下实现的,这时隧穿电子的能量高于分子光学带隙的宽度(∼1.9 eV).在这样的激发偏压下,虽然诸如非弹性电子散射机理和等离激元辅助能量转移等激发机理的贡献并不能完全排除[24],但是,我们通过分子发光强度的偏压依赖关系与分子电子态之间的关联,认为这种情况下分子激子的产生应该主要是通过载流子注入机理来实现的[14].

图2 STM诱导单分子电致发光的单光子发射特性[20] (a)吸附在3层和4层NaCl薄层上的单个ZnPc分子的STML光谱(−2.5 V,100 pA,30 s),红色和蓝色光谱中的尖锐发光峰来源于ZnPc分子的Q带跃迁,黑色光谱为针尖在金属衬底上时纳腔等离激元对应的STML光谱;(b)对应于图(a)中三种不同位置的STML光谱的二阶光子关联性测量;(c)−2.5 V偏压下吸附在4层NaCl薄层上的单个ZnPc分子的二阶光子关联性随隧穿电流(40—120 pA)的变化关系;(d)与(c)中二阶光子关联性相对应的g(2)(0)值(红色方框)和时间常数τ0(蓝色圆圈)随隧穿电流的变化关系Fig.2.Single-photon emission properties of the STM induced luminescence from a single ZnPc molecule[20].(a)STML spectra of a single ZnPc molecule adsorbed on 3 and 4 monolayer(ML)of NaCl(−2.5 V,100 pA,30 s).The sharp emission peaks in red and blue spectra are originated from the Q-band transition of the ZnPc molecule,while the black curve corresponds to the STML spectrum of the nanocavity plasmon when the tip is above the metal substrate.(b)Second-order correlation measurements of the emitted photons corresponding to the STML spectra at three different sites in(a).(c)Second-order correlation measurements of the single ZnPc molecule adsorbed on 4 ML of NaCl for different tunneling currents(40–120 pA)under the bias-2.5 V.(d)Estimated g(2)(0)values(red squares)and time constant τ0(blue circles)at different tunneling currents.
由于光子发射的统计特性可以通过测量光子之间的相关性来判断[31−34],因此,我们搭建了与STML技术相结合的Hanbury-Brown-Twiss(HBT)干涉装置,这是一种光子发射的符合计数测量技术,可以测量隧穿电子激发下分子发光的二阶关联函数[g(2)(τ)].如图2(b)所示,对于吸附在3层和4层NaCl薄膜表面的ZnPc分子发光而言,相应的二阶相关函数曲线上均表现出了显著的光子反聚束凹谷特征,而对于NCP的发光而言,却没有观察到任何的凹谷特征.这表明,单分子的电致发光具有清晰的光子反聚束效应,即其光子发射具有明显的单光子发射特性.
单光子发射的纯度可以通过对实验数据进行指数拟合来进行估算: g(2)(τ)= 1−[1 − g(2)(0)]e−|τ|/τ0. 对于吸附在4层NaCl上的ZnPc分子,估算的g(2)(0)值为0.12(2),而对于吸附在3层NaCl上的ZnPc分子,估算的g(2)(0)值为0.41(4),二者都小于单光子发射的判据阈值0.5[35,36].此外,与荧光过程相关的时间常数(τ0)也可以通过二阶关联函数的测量来估算.对于吸附在3层和4层NaCl上的ZnPc分子,相应的τ0值分别为0.48(5)ns和1.26(3)ns.结合3层NaCl上的ZnPc分子的发光强度要比4层NaCl上的分子弱得多的现象,较短的时间常数说明较薄的NaCl脱耦合层具有较大的非辐射衰变速率,荧光淬灭效应较强.图2(c)给出了在不同隧穿电流激发下的吸附在4层NaCl上的ZnPc分子对应的二阶关联函数曲线.如图2(d)所示,在相同的NaCl脱耦合层厚度下,随着隧穿电流的增大,针尖逐渐逼近分子,分子的辐射跃迁速率以及非辐射速率也会增大,从而导致所测量的时间常数变短.对时间常数的测量与分析可以被用来研究位于金属附近和等离激元纳腔内的单个分子中激子的产生与衰减等动力学过程[20,34].特别值得一提的是,对于这种金属作为衬底的样品结构,即便分子与探针之间的间隔小到1 nm以下,分子荧光的量子效率仍然随着距离的减小而增加,这种规律是与之前分子在玻璃衬底样品的光致荧光研究中报道的金属纳米颗粒的短距离淬灭现象不同的.
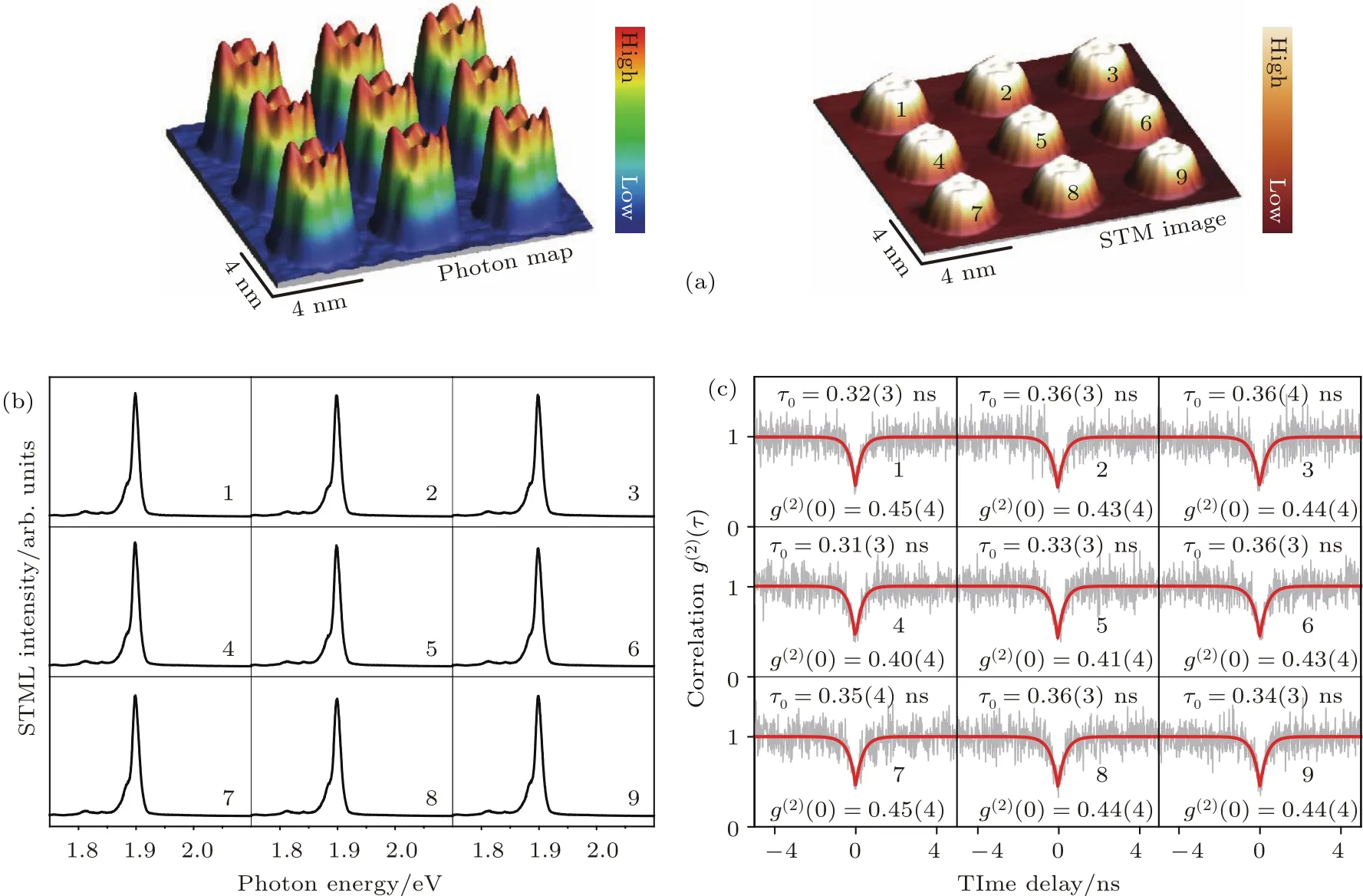
图3 人工构建的单光子发光体阵列[20] (a)在吸附在3层NaCl薄膜上的通过STM人工构建的3×3的ZnPc单分子阵列上同步采集的光子图(上图)与STM拓扑图(下图);(b)和(c)为相应于(a)中9个分子对应的STML光谱(−2.5 V,300 pA,10 s)与二阶光子关联性测量结果(−2.5 V,300 pA)Fig.3.Artificially constructed single-photon emitter array[20].(a)Simultaneously acquired photon map(top)and STM image(bottom)of a 3 ×3 ZnPc molecular array on 3 ML NaCl through STM manipulation(−2.5 V,50 pA,14×14 nm2).(b),(c)STML spectra(b),−2.5 V,300 pA,10 s and second-order correlation functions(c),−2.5 V,300 pA acquired from corresponding ZnPc molecules marked with numbers in(a).
由于STM具有非常强的单分子操纵能力,所以可以利用STM来构筑特定的分子结构.如图3所示,我们利用STM操纵,在3层NaCl衬底上构建了一个3×3的ZnPc分子阵列结构,分子间距为∼4.4 nm.图3(a)的下图给出了分子阵列的STM图像,上图给出了同步采集的光子图.如图3(c)和图3(d)所示,分别对阵列中不同的分子进行STML光谱和二阶关联函数g(2)(τ)测量,我们发现阵列中不同的单个ZnPc分子都表现出非常相似的发光特征,即每个分子都具有相似的发光光谱和单光子发射特征(即反聚束的“凹谷”特征,相应的g(2)(0)值都小于0.5).这样一来,我们就构筑了一个几乎全同的单光子源阵列.这些单分子电致发光和单光子发射研究结果,不仅为在纳米尺度上研究金属附近分子的光物理现象提供了新的手段,也为研发面向光电集成量子技术的电泵单光子源提供了新的思路.
3 分子间偶极-偶极相干耦合的可视化
在第2节中我们展示了如何利用STM操纵来构建单光子源阵列,其中每个分子的发光特性都几乎相同而且与孤立的分子单体很类似.这表明当分子间距为大约4 nm时,两个分子间的相互作用是可以忽略不计的,可作为孤立的单分子来处理.那么一个随之而来的问题是:如果两个分子之间的距离变得足够近的话,它们的光谱特征会发生什么变化呢?
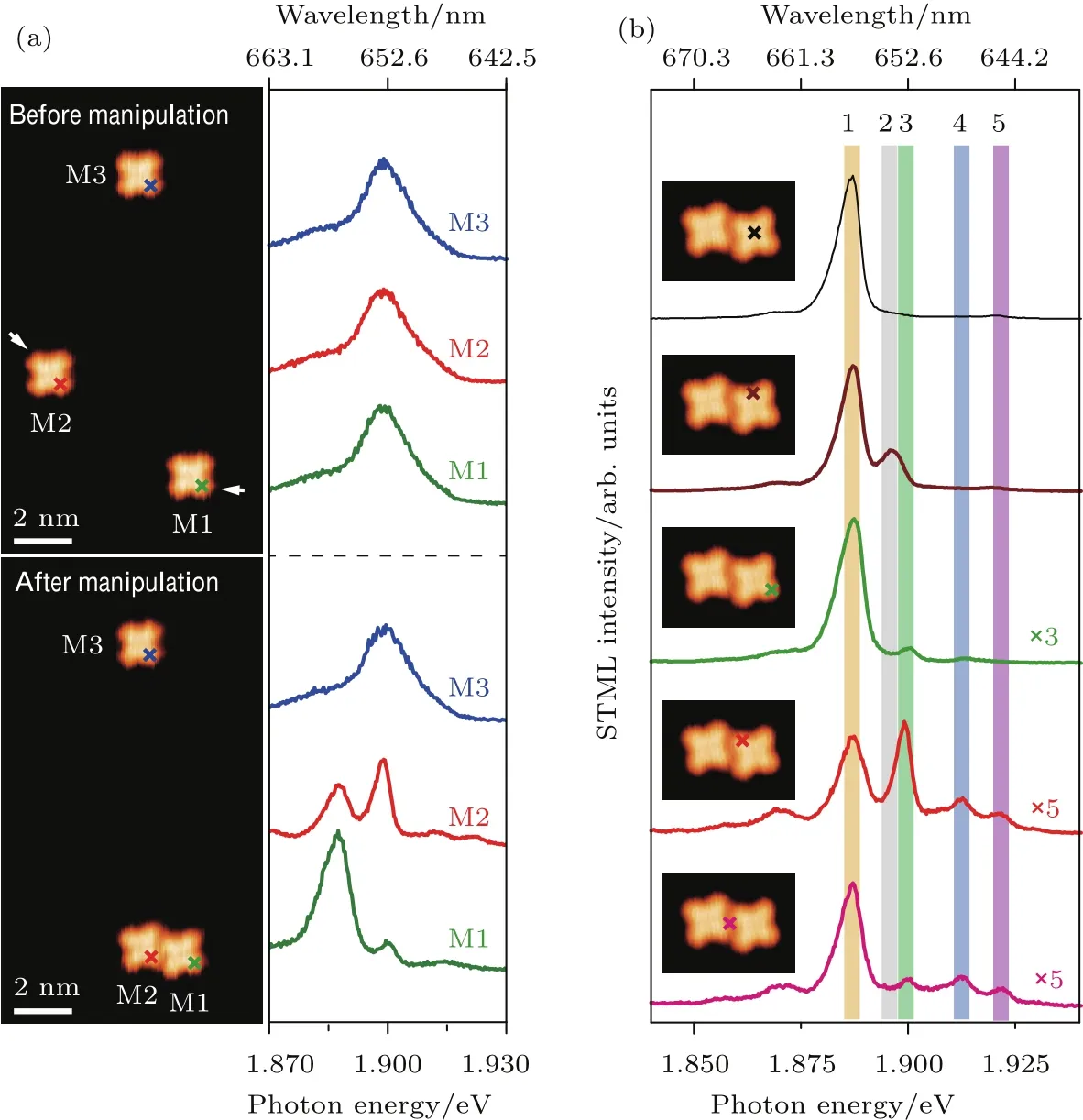
图4 单个ZnPc分子与人工构造分子二聚体的STML光谱比较[14] (a)STM操纵前后对应的STM拓扑图(左图 −1.7 V,2 pA)与STML光谱(右图 −2.5 V,200 pA,60 s);(b)分子二聚体内不同位置的STML光谱(−2.5 V,200 pA,60 s),可以识别出5个特征峰Fig.4.STML comparison between an isolated ZnPc monomer and an artificially constructed molecular dimer[14]:(a)STM topograph(left,−1.7 V,2 pA)and corresponding STML spectra(right,−2.5 V,200 pA,60 s)before and after manipulation;(b)site-dependent STML spectra(−2.5 V,200 pA,60 s)corresponding to different positions inside the molecular dimer,in which 5 emission peaks can be identified.
如图4(a)所示,我们利用STM操纵将两个孤立的ZnPc分子(M1和M2)推到一起,构成了一个分子中心间距约为1.45 nm的ZnPc分子二聚体.利用STML技术,将一定能量的隧穿电子注入到STM探针下方的分子,将其激发至激发态,并测量二聚体的电致发光光谱(图4(a)右图).我们发现二聚体的STML光谱特征变得与孤立的单个分子(M3)完全不同,谱峰发生了明显劈裂.进一步通过在ZnPc分子二聚体的不同特征位点处来激发分子二聚体,发现分子二聚体主要有5个特征荧光峰,分别对应于5个模式(如图4(b)和图5(a)所示).分子二聚体STML光谱特征的变化表明,当分子通过库仑作用相干地耦合在一起时,从STM探针局域注入的电子激发能量迅速地被整个分子二聚体所共有,其单体特征消失了,即分子二聚体构成了一个单激子量子纠缠体系.
为了给出这5个发光模式的全景图像,我们在扫描过程中逐个像素点记录相应的STML光谱,从而得到具有亚纳米空间分辨的光谱成像,如图5(b)所示.针对不同发光峰进行积分,我们发现不同发光峰所对应的发光产率空间分布的特征各不相同,而且与单个分子的光子图成像特征也有很大的不同.单个ZnPc分子与分子二聚体各个模式之间的光子图像特征上的差异也表明,当两个ZnPc分子形成分子二聚体后,单体原有的量子特征就消失了,分子二聚体的光谱特征由新的激发态决定.
二聚体的单激子激发态的波函数可以表示为单体波函数直积的叠加,即: Ψdim,e=(ψ1,eψ2,g±ψ1,gψ2,e其中,下标1或2表示波函数分别归属于单体1或者单体2,下标e或g分别表示激发态或基态.这种叠加态意味着二聚体的量子态必须要从整体来考虑,其中单体的孤立量子特性已经消失,单体可以同时部分处于基态和激发态,但其所处的量子态与另一个单体所处的量子态相关联:即单体1处于激发态时单体2处于基态,反之,单体1处于基态时单体2处于激发态.这意味着能量可以相干地在单体1和单体2间振荡,形成离域的激子.此时,二聚体体系的能量会发生劈裂(图2(d)),相关的激子劈裂能可以表示为J=其中,为相互作用微扰项.这样一来,如图5(c)所示,对于一个相干耦合的分子二聚体,相应的光学跃迁能量∆Edim可以写为∆Edim=∆Emono−∆W±|J|,其中∆Emono为孤立的单个分子的跃迁能量,∆W为由于分子间的范德华相互作用导致的能级移动.令人惊喜的是,二聚体中分子之间的这种相互作用和光谱演化可以借助偶极-偶极相互作用模型来加以理解.在点偶极近似模型[37,38]下,激子劈裂能|J|:J=[µ1·µ2−3(µ1)(µ2)]/(4πε0r3),其中µ1(µ2)为对应于分子单体的跃迁偶极距(偶极大小为µ0),r为两分子的中心间距,间距大小为r=|r|,方向为ˆr.由于单个ZnPc分子具有两个简并的激发态,分别对应于沿着x和y轴方向具有相同大小的两个互相垂直的跃迁偶极距,所以分子二聚体会有5种不同的偶极耦合模式:共线同相位(→→)、共线反相位(→←)、平行同相位(↑↑)、平行反相位(↑↓),和垂直正交(↑→与→↑). 对于这些不同的偶极耦合模式,相应的偶极耦合强度可以分别写为:J→→= −J→←= −/4πε0r3,J↑↑= −J↑↓=/4πε0r3和J↑→=J→↑=0.根据偶极耦合强度的大小以及正负关系(图5(d)),可以把图5(a)中的5个发光峰与5种偶极耦合模式关联起来.
我们基于点电荷理论模型[14]计算出了不同偶极耦合下的光子图的图案,并将理论计算出来的图案特征与实验获得的光子图相比较.如图5(b)所示,我们发现实验获得的光子图的发光强度最大值的位置以及图像节点的位置和数目都与理论图像符合得较好,这又进一步支持了我们对发光峰所对应偶极耦合模式的归属.实验图像中的一些细节特征可能与隧穿电子对分子的激发过程有关,反映了分子电子态的空间分布特征.
值得一提的是,不同偶极耦合构型的光谱成像图案具有类似σ或π成键反键轨道的空间分布特征(图5(b)).这些空间特征不仅反映了分子二聚体的局域光学响应特性,而且还直观地揭示了分子二聚体中各个单体跃迁偶极之间的耦合方向和相位信息.特别地,模式1与模式4对应的跃迁偶极组合方式由于其耦合相位同相可以被归属为超辐射(superradiance)模式,而模式2与模式5则由于耦合相位相反,属于亚辐射(subradiance)模式.对亚辐射模式而言,由于远场观察下的净偶极为零,所以通常无法被远场观察到,也被称为“暗(dark)”模式.在这里,之所以这样的“暗”模式能够被探测到,是因为针尖-衬底构成的纳腔中由于针尖相对于分子中心的位置导致的非对称的镜像偶极效应,进而被纳腔放大为远场信号的结果.由于可以同时探测到超辐射与亚辐射模式,这使得我们可以对偶极耦合强度|J|进行直接测量,对于共线组合模式和平行组合模式相应的耦合强度分别为17.3(3)meV和8.2(3)meV.由于位于针尖下方的单个分子被隧穿电子激发后,激发能量会快速分享给邻近分子,然后能量在两个分子之间来回振荡传递,从而实现两个分子的纠缠与耦合.从实验测量得到的耦合能,可以估算出相应的振荡频率大约在1013s−1数量级,这一数值远远地快于振动弛豫过程的时间[39].由此看来,ZnPc分子与金属衬底之间通过NaCl薄层的有效脱耦合,更易于实现分子二聚体中的偶极-偶极相干相互作用的观测.

图5 ZnPc分子二聚体内相干偶极耦合的实空间成像[14] (a)二聚体的典型STML光谱(−2.5 V,200 pA,60 s)及其5个特征峰;(b)对应于五个发光峰的二聚体内不同偶极组合模式(左图)与相应的实空间光子图成像(中图−2.5 V,200 pA,每个像素点采集时间为5 s,图像大小为5 nm×4 nm,33×22像素),基于点电荷模型的理论模拟图如右图所示;(c)分子二聚体的能级示意图;(d)偶极耦合模型对应的能级劈裂图Fig.5.Real-space mapping of the coherently coupled ZnPc dimer[14]:(a)Typical STML spectra(−2.5 V,200 pA,60 s)with five distinctive emission peaks;(b)schematic arrangements of the transition dipoles in the ZnPc dimer(left)and corresponding real-space photon images(−2.5 V,200 pA,5 s per pixel;the image size is 5 nm×4 nm,34×22 pixels)for five emission peaks;the theoretical simulations based on the point-charge model is shown on the right panel;(c)the band energy diagram of a molecular dimer;(d)the energy splitting diagram for different dipole-dipole coupling modes.
由于共线同相位的偶极耦合模式可以产生大的总偶极距和强的超辐射,所以在分子二聚体的基础上,我们进一步构建了由3到4个ZnPc分子组成的分子链体系,如图6(a)所示,图中还给出了二聚体、三聚体和四聚体的共线同相位超辐射模式对应的实空间光子成像图样,以及相应的理论模拟结果.从图6(b)给出的STML光谱可以发现,分子链的辐射强度随着分子数目的增加而不断变强.进一步分析辐射增强因子R随分子数目N的变化关系(如图6(c)所示),在分子数目很少时辐射强度基本上随N呈线性变化的关系,但当分子链较长时(N>3),数据出现了偏离,这可能来源于纳腔等离激元局域场的有限的空间分布范围,还有待进一步研究.偶极耦合是激发状态下分子间库仑相互作用的一种基本形式,对分子材料和生物体系中的能量转移过程以及量子光学中纠缠体系的构筑均起着关键性的作用.这里展示的在亚纳米分辨的水平上研究分子间相干偶极耦合的实空间光学特征的能力,将为在单分子水平上研究分子间的相互作用和能量转移提供新的途径.

图6 ZnPc分子链中的超辐射现象[14] (a)由1—4个ZnPc分子构成的分子链体系对应的跃迁偶极分布(第一行),STM形貌图(−2.5 V,2 pA;第二行)、实空间STML光子图成像(−2.5 V,200 pA,5 s/pixel;第三行),对应的谱峰积分范围从左到右分别为(1.899±1.5),(1.887±1.5),(1.880±1.5)和(1.875±1.5)meV,第四行是共线同相位偶极耦合模型得到的理论模拟光子图图样;(b)对应于(a)中第二行“×”标记位置的STML光谱(−2.5 V,200 pA,60 s);(c)分子链超辐射模式的辐射增强因子R随分子数目N的变化关系(蓝色方框),其中红色曲线表示理想条件下R=N的变化关系Fig.6.Superradiance of the ZnPc molecular chain[14]:(a)Schematic arrangements of molecular transition dipoles(first row),STM topograph(−2.5 V,2 pA,second row),real-space STML photon images(−2.5 V,200 pA,5 s/pixel,third row),corresponding to the integration ranges(left to right)as(1.899±1.5)(1.887±1.5),(1.880±1.5)and(1.875±1.5)meV,the fourth row corresponds to the simulated patterns based on the in-line in-phase coupled dipole models;(b)STML spectra(−2.5 V,200 pA,60 s)corresponding to the ‘×’positions marked in the second row of(a);(c)the emission enhancement ratio R of the superradiant modes of the molecular chains as a function of the molecular number N(blue squares),in which the red curve represents the ideal R=N relation.
4 等离激元纳腔中的单分子Fano共振效应
在第2,3节中,我们在亚纳米尺度上利用高度局域的隧穿电子激发分子发光,并利用纳腔等离激元作为局域放大器来增强分子的发光信号.事实上,高度局域的隧穿电子也可以被用来在空间不同位置可控地激发纳腔等离激元,为研究等离激元场与分子间的相互作用提供有用的信息.当一个发光体与纳腔等离激元发生共振相互作用时,由于发光体的离散态跃迁与纳腔等离激元的连续态跃迁之间的相干耦合会发生量子干涉,从而导致光谱的线型发生变化,这就是Fano共振效应[21,25,28].如图7所示,当STM针尖(也就是相应的等离激元纳腔)位于孤立的脱耦合的单个ZnPc分子近邻位置时,通过利用隧穿电子激发纳腔等离激元,并通过等离激元与分子相互作用,就可以观察到Fano共振效应.
当STM针尖位于ZnPc分子正上方时(如图7(b)中的蓝色圆点和图7(c)中的情形I所示),分子直接被隧穿电子所激发,从而产生尖锐的分子发射峰.另一方面,如果针尖位于远离分子的衬底上方(如图7(b)中的绿色圆点和图7(c)中的情形III所示),则会观察到一个展宽约为160 meV的等离激元发光峰.当把针尖移动到ZnPc分子近邻位置时(如图7(b)中的红色圆点和图7(c)中的情形II所示),在宽的等离激元背景光谱上,叠加了一个清晰的“凹谷”,而且谷底的位置与ZnPc分子的发光峰位密切相关.这种典型的Fano线形的光谱特征表明分子跃迁与纳腔等离激元共振之间存在相干耦合过程.
通过利用STM技术的原子级分辨的空间定位能力并且精确控制单分子与STM探针之间的相对距离,可以调控分子与STM探针-衬底纳腔之间的耦合强度.当针尖从ZnPc分子边缘沿着图中所示路径逐渐远离分子时,相应的光谱也从具有Fano线形特征的STML光谱逐渐演化为宽的纯粹的等离激元发光光谱(如图8(a)所示).换句话说,当针尖逐渐靠近分子时,Fano凹谷会逐渐变宽变深,这表明ZnPc分子与纳腔等离激元之间的耦合强度在逐渐变强.这样一来,我们就可以通过对凹谷深度的分析,了解分子与纳腔等离激元间的相互作用强度.通过对凹谷深度进行归一化处理,我们发现其随着间距的增大呈现出指数衰减的特性,估算的衰减长度只有∼0.9(1)nm.这表明纳腔等离激元的有效作用距离也被高度限域在约1 nm范围内.通过利用修正的偶极耦合模型[21]对归一化的凹谷深度进行定量分析,我们可以估算出相应的耦合强度大小,其值最大可以达到∼15 meV,如图8(b)所示.

图7 单分子Fano共振效应[21] (a)基于单个ZnPc分子电致发光的单分子Fano共振实验示意图;(b)单个ZnPc分子的STM形貌图;(c)对应于(b)中标记的三种不同的单分子-等离激元纳腔结构组合(上图)与对应的STML光谱(下图;−2.5 V,200 pA,20 s)Fig.7.Single-molecule Fano resonance effect[21]:(a)Schematic of experimental setup for single-molecule Fano resonance based on the electroluminescence of a single ZnPc molecule;(b)STM topograph of a single ZnPc molecule;(c)three type of single-molecule/plamonic-nanocavity configurations(top)and corresponding STML spectra(bottom,−2.5 V,200 pA,20 s).
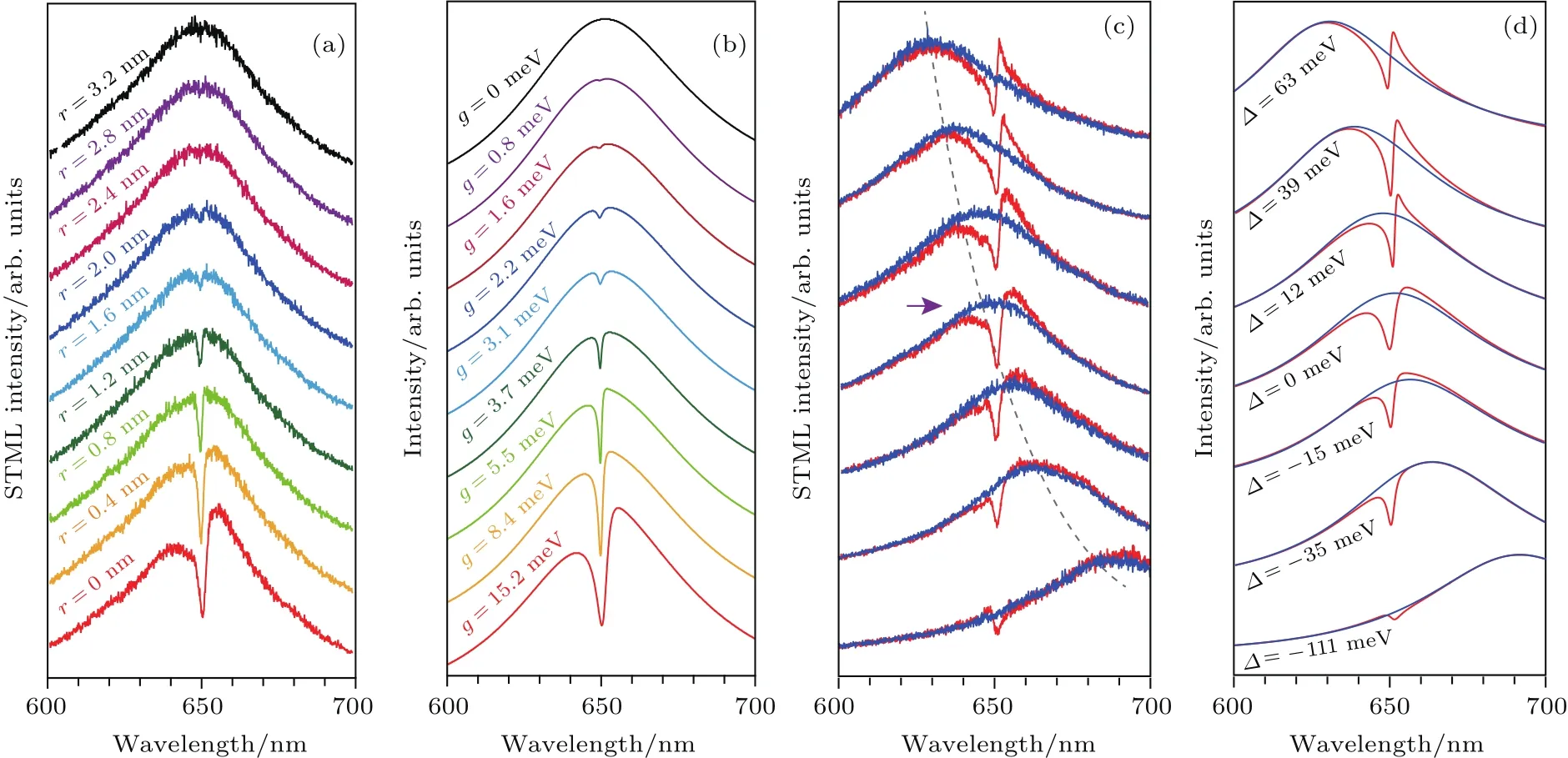
图8 单分子Fano共振效应的调控[21](a)针尖从ZnPc分子边缘远离时相应的STML光谱的变化(−2.5 V,200 pA,20 s);(b)对应于(a)的具有不同耦合强度的理论模拟光谱;(c),(d)分别为实验(−2.5 V,200 pA,20 s)和理论对应的不同能量失谐条件下的Fano光谱Fig.8.Tunable single-molecule Fano resonance[21]:(a)Distance dependent STML spectra when the tip is moved away from the ZnPc molecule’s edge;(b)simulated spectra with different coupling strength corresponding to(a);(c),(d)are the experimental(−2.5 V,200 pA,20 s)and theoretical Fano spectra under different detuning conditions.
通过改变STM的针尖形貌,可以调节纳腔等离激元共振频率,使之相对于分子跃迁频率具有不同的能量失谐值,进而研究不同能量失谐对单分子Fano共振的影响.如图8(c)所示,NCP的共振频率可以从620 nm调节到690 nm(蓝色谱线),相应的Fano光谱(红色谱线)也表现出不同的非对称光谱特征.需要指出的是,即使是在能量零失谐的条件下,Fano线形也依然表现出一定的非对称性,这表明等离激元与分子之前的相互作用已经不能用简单的点偶极耦合模型来解释,而是需要考虑分子跃迁偶极的空间分布与纳腔等离激元模式的高阶效应的影响.此外,我们还观察到了Fano凹谷的反常位移,谷底位置最大可以移动3 meV,可以认为是由于单分子在强等离激元场中的自相互作用导致的Lamb位移所致.
下面我们将从分子跃迁偶极与等离激元局域场的矢量属性出发,对Fano凹谷的反常位移进行进一步探究.在前文中我们曾指出,ZnPc分子具有D4h对称性,存在两个正交简并的跃迁偶极距(px和py),分别沿着分子瓣的方向(如图9(a)中的绿色和橙色箭头所示),因此当把STM针尖放置在相对于分子的不同取向和位置时,分子与纳腔等离激元之间的相干耦合也会由于跃迁偶极与局域场的矢量性而出现不同.通过将STM针尖沿环形路径(如图9(a)中的红色虚线所示)绕分子一周,我们对取向依赖的STML光谱进行了测量.图9(b)给出了在零失谐条件下针尖位置相对于分子的两个不同取向(0◦和45◦)对应的Fano光谱.可以发现,这两条光谱几乎是重合在一起的,只有把Fano凹谷对应的区域放大后才会观察到很小的频率移动,如图9(b)中的插图所示.进一步将Fano光谱按照针尖位置的不同取向角度从0◦到360◦做图 (如图9(c)所示),可以得到一个周期性花样,四个周期正好对应分子的四个瓣结构,其中0◦,90◦,180◦和270◦对应的是针尖位置靠近ZnPc分子四个瓣时测量的光谱,Fano凹谷表现出大的Lamb 位移(∼3 meV);45◦,135◦,225◦和315◦对应的是针尖位于ZnPc分子瓣之间的情形,相应的Lamb位移较小(∼1 meV).对于不同能量失谐条件下的Fano光谱,我们都观察到了类似的周期性变化特征.我们认为这样的周期性变化是因为光学Lamb位移本身是与分子跃迁偶极距与纳腔结构对应的格林函数有关的,一般可以写为由于格林函数的并矢特性与跃迁偶极的矢量性,因此,Lamb位移的大小也具有了取向依赖性.由于真实的针尖-衬底体系对应的格林函数无法准确知晓,因此,我们只有唯像地用cos4θ和sin4θ来近似描述针尖位置相对于分子跃迁偶极px和py不同取向时的角度依赖关系,并且通过理论模拟得到了Fano光谱及相应的Lamb位移与实验观测到的光谱特征符合得很好,如图9(d)所示.这种对针尖位置和取向依赖的特性,也表明单个分子与纳腔等离激元之间的相干耦合过程存在着各向异性,揭示了纳腔等离激元场和分子跃迁偶极的矢量特征、以及纳腔等离激元场除主导的轴向分量外还具有可观水平分量的重要信息.对单分子Fano共振效应在空间上的原子级别的调控能力,表明了纳腔等离激元以及分子-等离激元耦合强度分布在空间上具有高度限域的特征,也为探索相干耦合的物理机理提供了新的思路.
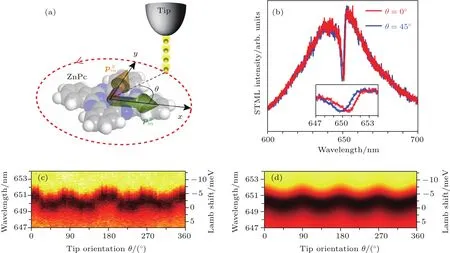
图9 单分子Lamb位移的取向依赖关系[21] (a)单分子Fano共振的取向依赖关系测量示意图;(b)两种典型条件下(0◦和45◦)对应的单分子Fano光谱(−2.5 V,200 pA,5 s);(c),(d)分别为实验和理论对应的Fano凹谷随针尖取向的变化Fig.9.Orientation dependent single-molecule Lamb shift[21]:(a)Schematic of orientation dependent measurement of the single-molecule Fano resonance;(b)two typical single-molecule Fano spectra(−2.5 V,200 pA,5 s)with the orientation angle of 0◦ and 45◦,respectively;(c),(d)are the experimental and theoretical results for the Fano dip varying with the tip orientations,respectively.
5 总 结
本文综述了本研究组近期在单分子电致发光与分子光量子态调控方向的最新进展.我们利用STM诱导发光技术,通过有效的电子脱耦合与纳腔等离激元调控,实现了单个分子的电致荧光,并证明了单个分子在隧穿电子激发下的电致荧光现象具有单光子发射特性;发展了具有亚纳米空间分辨的荧光光谱成像技术,实现了对分子间相干偶极相互作用特征的实空间观察;通过精确控制分子与探针之间的距离,调控了分子与纳腔等离激元之间的相干相互作用,在单分子水平上观察到了法诺共振和兰姆位移效应.在此基础上,如何实现单分子与STM隧道结中纳腔等离激元间的强耦合并研究其特性将是未来单分子电致发光领域的一个重要问题.此外,STML技术与超快时间分辨测量技术的结合也将是一个重要的研究方法的发展方向,并将提供单分子尺度上的激发态演化动力学信息.总之,单分子尺度的电致发光研究不仅可以为深入理解单个分子及其耦合系统的光学特性提供丰富的信息,并且可以为研发基于分子体系的纳米光源、单光子源、捕光天线系统以及纳米光电器件等提供科学依据.
感谢中国科学技术大学侯建国院士、杨金龙教授、罗毅教授、王兵教授,以及西班牙材料物理中心Javier Aizpurua教授的合作与讨论;感谢张力博士、骆阳博士、孟秋实博士、郁云杰博士等在实验数据采集与分析上的贡献.
