核磁共振量子信息处理研究的新进展∗

孔祥宇 朱垣晔 闻经纬 辛涛 李可仁 龙桂鲁2)†

1)(清华大学物理系,低维量子物理国家重点实验室,北京 100084)

2)(量子物质科学协同创新中心,北京 100084)

(2018年4月20日收到;2018年5月24日收到修改稿)

1 引 言

量子信息是量子力学和信息科学的交叉学科,与传统信息科学相比,量子信息包含完全不同于以往经典概念的特性,如波粒二象性、量子纠缠、量子态叠加等.量子计算起源于1980年,Benio ff[1]试图运用量子力学来进行可逆计算以减少热能耗散,Feynman[2]则从高效量子模拟的角度出发,两人分别独立地提出了量子计算的概念.很少为人知晓的是,苏联科学家Manin[3]也在同时期提出了量子计算的思想.由于量子的并行性,量子计算处理数据和存储数据的能力与经典计算相比要显得更强大.自1995年以来,量子计算逐渐成为国际上最炙手可热的研究前沿,多种可能实现量子计算机的方案相继被提出.DiVincenzo[4]在2000年总结了实现量子计算的潜在物理体系需要满足的五项要求.其中,最为重要的一点是该系统应该具有可扩展的量子比特.迄今为止,核磁共振系统、超导约瑟夫森结、金刚石色心、离子阱、量子点等物理体系因各自不同的优点,成为建造通用量子处理器的热门候选者.在这篇综述中,我们仅限于讨论当前量子信息处理中有关液态核磁共振的技术和成果.

1946年,Bloch和Purcell观测到处于强磁场中的核自旋可以吸收和发射具有共振频率的电磁辐射.此后核磁共振(NMR)技术得到迅速发展与应用,不仅可以用于分析化合物结构,而且能够进行医学成像、探矿等.1998年,Chuang,Laflamme和Cory等提出可以将核磁共振系统作为量子信息处理器[5−7],从而开启了核磁共振量子计算这一研究方向.与其他量子计算系统相比,核磁共振系统在噪声环境下具有较强的鲁棒性,具有长相干时间,可以实现对量子比特精确的控制[8].近年来,核磁共振平台上的一些量子控制技术,不仅提高了基于核磁共振的量子信息处理的能力,而且为操控其他量子系统提供了技术和启发.例如,梯度上升脉冲方法(GRAPE)[9],通过计算梯度和优化目标函数,实现对量子系统的高精度优化操控.该技术目前已被广泛用于超导电路、离子阱和金刚石色心等量子计算平台中.最近,这一技术又取得了新的进展,在GRAPE中,优化目标函数和梯度的计算是在经典计算机上完成,花费的计算时间随着系统的增大而呈指数增加.最近基于GRAPE技术[10−12]发展起来的测量量子反馈控制技术(MQFC)可以在所研究的量子体系中完成对量子信息处理器目标函数和梯度的计算,也就是在量子系统中进行计算,一方面加快了优化速度,一方面能修正系统误差.MQFC技术已经在12个量子比特的核磁共振系统上进行了高精度优化控制的验证.另一个重要发展是Laflamme研究组提出的“脉冲编译器方法”,以解决GRAPE技术在高比特量子系统[13,14]中的不可拓展性.在核磁共振的发展过程中一些重要的理论也被应用到其他方面,比如,平均哈密顿理论[15]是利用脉冲序列对核自旋内部哈密顿量进行调制的普遍方法,被广泛用于设计解耦序列,如WHH4和WHH16[16,17].基于平均哈密顿理论的动力学解耦技术,可以消除或减少自旋和环境之间的相互作用,从而延长量子态的相干时间[18−20].此外动态解耦技术还可以与量子门相结合,通过实现动力学解耦序列之间的协同操作可以保护量子门操作[21,22].绝热量子计算是通过缓慢调节系统的哈密顿量进而实现目标哈密顿量从初态到目标态的演化,通常用于研究多体量子系统的基态性质[23−25].

另一方面,核磁共振技术的发展使得许多量子算法的演示成为可能,如Grover搜索算法[26−28]、Shor大数分解算法[29]、Deutsch-Jozsa算法[30]、Ordering-Finding算法[31]、Hogg算法[32]和线性方程求解的算法[33].值得一提的是,非绝热和乐量子计算也首先在核磁共振[34,35]中得到实现.而且,核磁共振系统作为一个量子模拟器,可以用于模拟基本量子力学模型、量子延迟选择[36,37]、量子相变[38,39]、量子隧道效应[40,41]和其他不易操控的量子系统等.核磁共振量子处理器还可用于探索隐变量理论和量子力学基本原理的研究,包括量子隐形传态、量子超密编码、波粒二象性、波函数、Bell不等式、超导现象研究[42−48]等.

本综述其余部分安排如下:第2节介绍核磁共振量子计算的基本原理,主要包括核磁共振物理系统的原理以及为了实现量子计算而发展的一些技术；第3—5节主要介绍利用核磁共振系统进行的研究工作,包括利用核磁共振系统已经实现的量子算法、利用核磁共振系统进行量子模拟的成果以及我们研究组发布的核磁共振量子云平台；在第6节,对核磁共振作为一个量子计算平台进行总结和展望,包括液态核磁共振的局限性、固态核磁共振的性质以及未来的发展方向.

2 核磁共振量子计算基础

在目前可用于进行量子计算的物理体系中,核磁共振系统具有相干时间长、量子门操作易于实现、实验技术完善等优势,是实验上实现可操控量子比特数较多以及演示算法数较多的物理体系之一.简言之,核磁共振量子计算的基本过程包括:以样品分子中的碳、氢等原子的核自旋在外加磁场的作用下形成的二能级系统作为量子比特,结合高精度的控制脉冲实现通用化的控制逻辑门[49],并通过探测自由衰减信号实现对末态结果的读取测量[50].

由于单个核磁矩信号很微弱,所以要产生可探测的信号就需要大量分子,这意味着核磁共振系统是一个宏观的系综系统,把处于特定环境下所有不可区分粒子的核自旋整体作为一个量子比特.所以可以取样品粒子中n个可区分的1/2自旋的核作为n个不同的量子比特,即该样品分子本身就是一台n量子比特的量子计算机.这里的可区分一般是指不同的元素,或者是化学位移不同的同一种元素.常用的两量子比特样品分子是13C标记的氯仿,三量子比特样品分子有13C标记的三氯乙烯,13C标记的丙氨酸,13C标记的氟代丙二酸二乙酯.为解决核磁信号微弱而采用系综系统也带来核磁系统的初始化问题,直到1997年Cory等[7]提出以赝纯态作为核磁共振量子计算初始态的方案才解决了这一问题.发展至今,典型的赝纯态制备方法有空间平均法[51−53]、时间平均法[54]、逻辑标记法[55]、猫态制备法[56,57]等.关于量子态的控制,通过控制外加射频脉冲来对核自旋进行任意角度的旋转,即可实现单比特操作,再利用核自旋间的J耦合作用可以实现两比特门,如CNOT门.而任意单比特逻辑门和CNOT逻辑门的实现则意味着通用量子门的实现.实际工作中,由于具体算法的量子线路拆解为基本逻辑门后数量很多,而且硬脉冲控制下的演化精度很低,所以一般会结合脉冲数值优化技术来提高对量子系统的控制精度,典型的有强调制脉冲技术(SMP)和GRAPE法.系综体系的量子态用密度矩阵来表示,量子计算的结果则通过施加一系列辅助脉冲来重构密度矩阵的方式获取,称为量子态重构(quantum state tomography).

2.1 赝纯态制备的“二步法”和“一步法”

在核磁共振体系中由于热平衡态是一个混合态,因此量子计算初始化便成了一个非幺正的过程.这个非幺正性,在空间平均法中通过梯度场实现；逻辑标记法通过约化到子空间实现,等价于测量操作；时间平均法则是利用多个幺正操作相加的非幺正性实现.但列举的这几种典型赝纯态制备方案都有不可回避的缺点,例如空间平均法会造成信号强度的损失,逻辑标记法则会带来比特资源的耗费,时间平均法需要重复实验等.近期我们组在理论与实践中发展出一些新的赝纯态制备方法,我们称之为“两步法”和“一步法”[58].接下来以这两种方法为例简要介绍赝纯态的制备过程.

首先以三量子比特系统为例说明“两步法”的赝纯态制备过程.核磁体系三比特系统的热平衡态的偏移密度矩阵为:

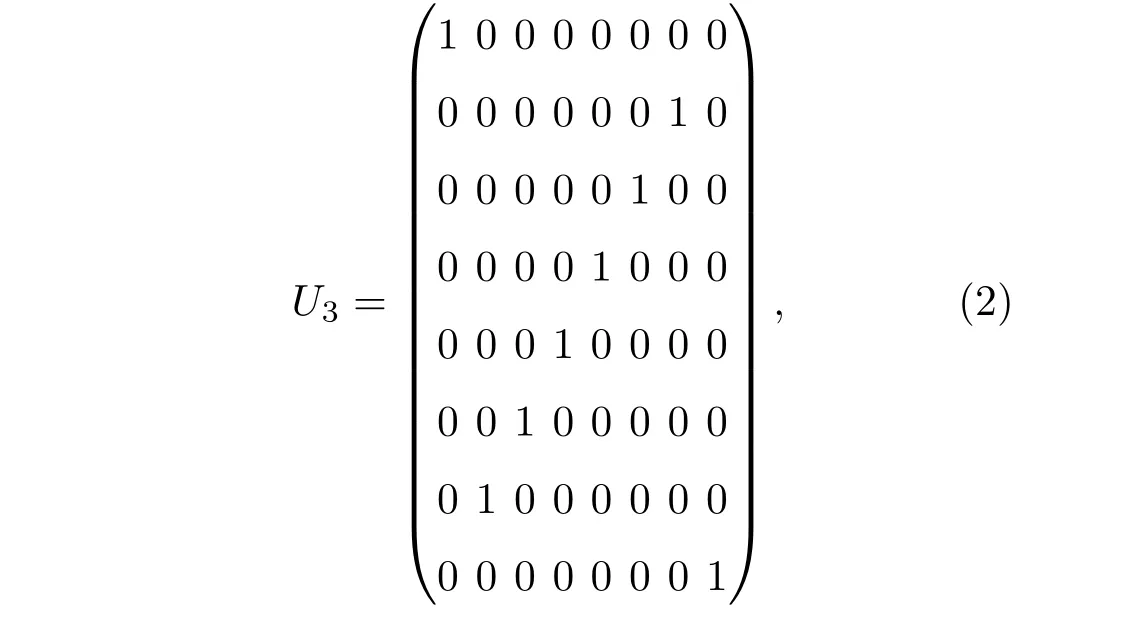
得到态:

将此态与热平衡态相加即得到如下形式的结果:

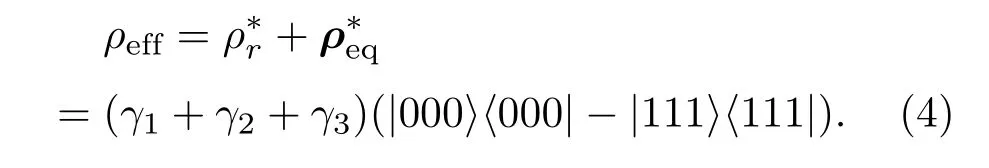
所以具体的实验制备过程是将热平衡态直接取样,再对热平衡态施加变换操作U3再采样,将两次采样的计算结果相加得到的密度矩阵在子空间中的形式等价于纯态.

对于一般量子比特热平衡态变换Un的通用量子线路如图1所示.

图1 幺正变换Un的量子电路Fig.1.The quantum circuit of unitary transformation Un.

两步方案结合了逻辑标记法和时间平均法的思路,同时最大程度地减小了比特资源的浪费,也不存在一次实验而多次使用梯度场对信号的减弱,而且对分子结构没有特殊要求,更减少了操作步骤,综合来看是一个相对以往算法性能更加优异的赝纯态制备方法.

除了“两步法”之外,还有操作步骤更为简单的称为“一步法”的有效纯态制备方案,该方案的核心思路是引入一个辅助比特,先对热平衡态做一系列的幺正变换,再对整个体系加一次梯度场,一次性地除去不需要的磁化分量,使最终密度矩阵在子空间的形式等价于纯态.一步法的量子线路如图2所示.

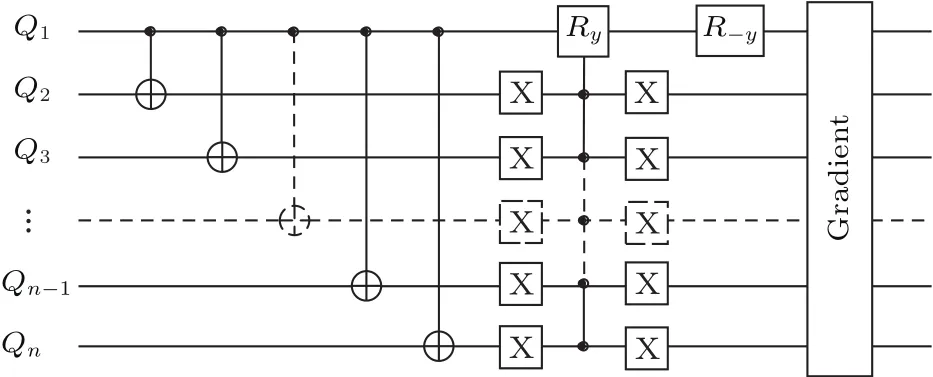
图2 一步法的量子线路图Fig.2.The quantum circuit of onestep algorithm.

一步法的核心思路与空间平均法类似,但在一定程度上减少了梯度场的使用次数以避免信号强度的严重损失,并且简化了操作流程,结合GRAPE脉冲优化算法可以实现高保真度的赝纯态制备.与之前在核磁共振中常用制备赝纯态的四种方法,我们进行了复杂性分析.如表1所示,其中f(n)表示与系统所包含的比特数n有关的函数,下标对应各类初始化方案的英文首字母,通常f(n)都是随着n的增大而不断增大的.而我们提出的一步法和两步法在随着系统维度增大时,实验采集次数、使用梯度场次、辅助比特使用个数都不依赖于系统所包含的比特数目.因此这两种方案因比特数目增加所带来的困难将会是最小的.而且我们给出了n比特的量子线路,结合自旋共振体系的GRAPE脉冲优化算法,这两种方案具有很强的拓展性.

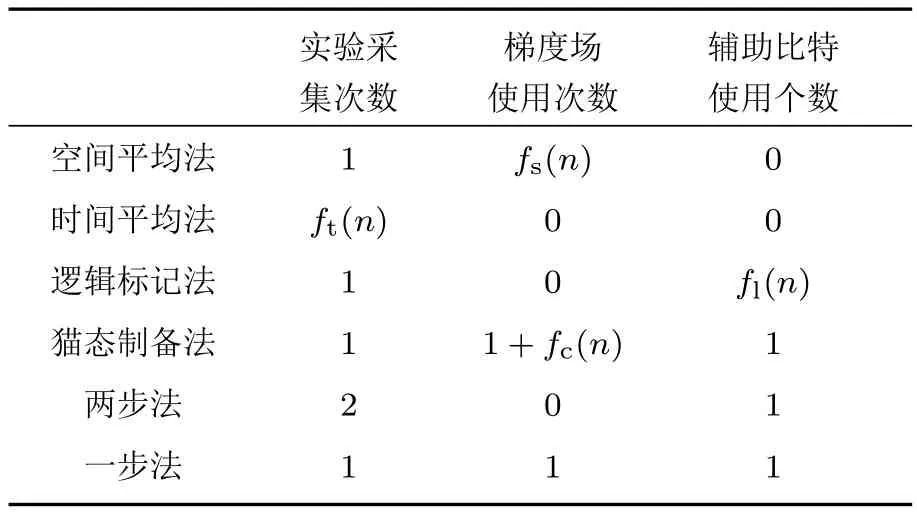
表1 两种方案与之前方案比较Table 1.The differences between the two protocols and previous protocols.

2.2 量子噪声注入技术

环境噪声是一把双刃剑,在一些特定的情况下噪声是不必要的,需要采取方法进行抑制,但是另一方面,噪声也是产生某些新奇物理现象的关键因素[59,60].例如观察CDD,UDD,QDD等DD序列在噪声下的演化,或者是研究特定噪声环境下开放系统的动力学行为,另外量子模拟也需要人为模拟一些噪声.因此有时需要在可控量子系统中构建人工噪声.这里介绍一些在核磁共振系统中注入各种噪声的方式,包括纵向弛豫噪声、横向弛豫噪声和混合噪声[61−63].

2.2.1 纵向弛豫噪声

在量子体系完全稳定的情况下,核磁共振系统的纵向弛豫是由控制场泄露或者幅度波动导致. 相应的哈密顿模型可以等价地写为HLR(t)=其中βx(t)为时域上具有正态分布的随机噪声,Ω是拉比频率,的形式如下:

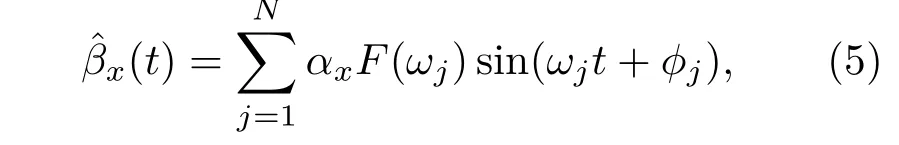
其中αi=x,y,z是噪声幅值;ϕj是随机相位;噪声频率ωj是基础频率ω0的整倍数,即ωj=jω0;Nω0确定高频截断点;函数F(ωj)是该模型的噪声谱函数.βx(t)时间关联函数写为

能量谱密度(PSD)可以表示为随机信号在频域的能量分布.应用Wiener-Khintchine理论,可以通过傅里叶变换得到PSD:

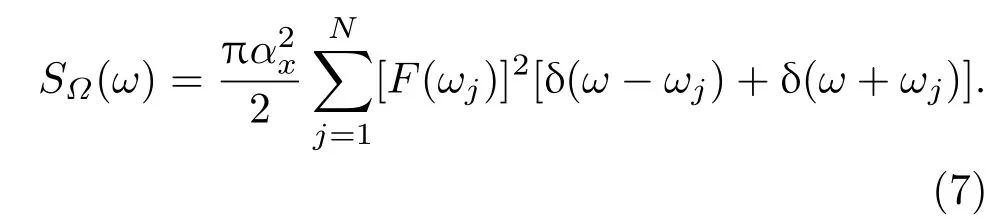
因此,可以用PSD模型来反求时域的噪声分布.例如,如果我们想模拟SΩ(ω)∼ωp,调制函数为F(ωj)=(ωj)p,由函数F(ωj)直接可以获得时域分布ˆβx(t).我们可以研究在此噪声模型下的量子系统的动力学行为.

2.2.2 横向弛豫噪声

横向弛豫噪声一般导致系统的退相干效应,主要源于核磁共振系统的不均匀性以及非静态的磁场等因素.与处理纵向弛豫噪声的方法类似,

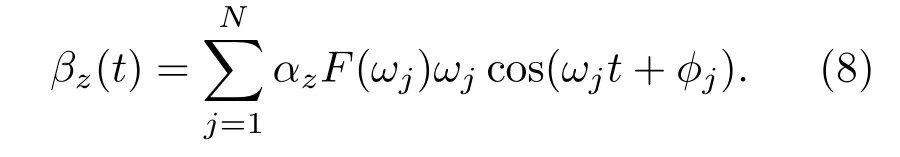
PSD和噪声谱函数F(ωj)可以写为

总之,由图3可知需要确定F(ωj)的函数形式以实现一般化的噪声PSD.

图3 各类噪声振幅和相位对比Fig.3.Various types of noise amplitude and phase contrast.

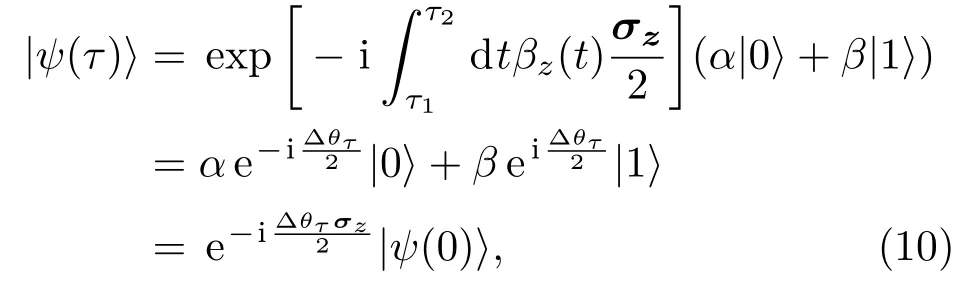
这里的∆θτ是βz(t)的积分,ωL表示拉莫频率.因此如果想要在退相干环境中模拟量子系统的演化过程,只需要在合适的时间点绕z轴转动∆θτ.

2.2.3 混合噪声

通过把上述两种噪声简单结合并不能得到混合噪声,因为βx(t)σx和βz(t)σz是不对易的.在满足共振条件ω=ωL的旋转坐标系中,存在混合噪声的控制场的系统哈密顿量为

考虑到绕z轴的旋转在核磁共振实验平台是不可直接实现的,我们一般把上述哈密顿量转换到相互作用绘景.在相互作用绘景中哈密顿量的形式为

当再变换到旋转坐标系,退相干效应的传播子为

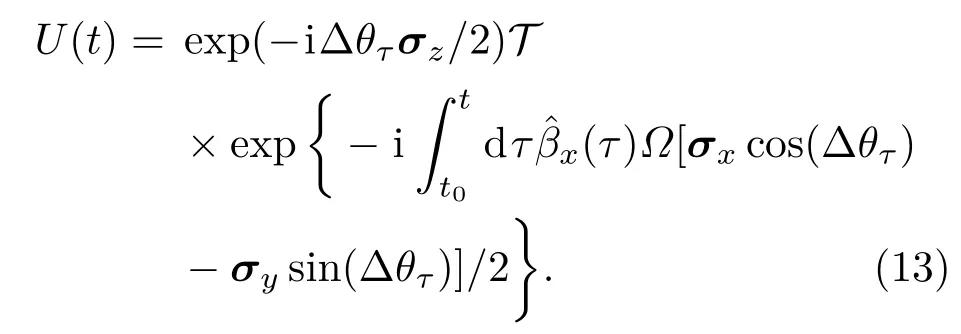
为了制造混合噪声环境,噪声波函数β(t)和θ(t)是人为引入的,并注入信号发生器以调制控制场脉冲.量子比特在x-y平面绕变动的轴以浮动的拉比频率转动,然后绕z轴转动角度∆θt.至此,我们提出了在可控系统中引入人工噪声的方法[63,64].值得注意的是,这里引入噪声的方法是在可控操作中加入噪声来模拟真实噪声环境,例如在核磁共振中就是在控制射频脉冲中加入噪声项.与用Kraus算子构造噪声信道是不同的,不存在辅助比特等资源的浪费,在现有各种体系中对控制技术做适当修正即可实现,也更符合实际的噪声产生情形.

2.3 量子态重构

核磁系统的实验样品并不是一个单独存在的分子而是大量全同分子组成的系综,因此核磁共振系统所做的量子态测量并不是投影测量,而是系综平均测量.当量子计算结束时,末态的核自旋会绕着静磁场方向进动并恢复到热平衡态,进动的核自旋就会在x-y平面的感应线圈内感应出电信号.因此核磁共振系统测量的物理量是横向磁化矢量,而横向磁化矢量信号会随着回复到热平衡态慢慢变成0,这个信号称为自由衰减信号(FID).感应线圈探测的自由衰减信号经过傅里叶变换得到频域中的实验谱图,根据这些谱图可以计算得出末态的矩阵元信息,从而实现量子态测量的目的.

设系统的末态密度矩阵为ρ(0),撤去控制脉冲后体系将在系统哈密顿量Hsys的控制下演化,演化方程为

所以第一个核的自由衰减信号:

在频率(ω1/2π−J/2)处谱峰的幅值与ρ13成正比,在频率(ω1/2π+J/2)处谱峰的幅值与ρ24成正比,所以ρ13和ρ24可测.同理对于第二个核可测ρ12和ρ34.由此可以看出如果只是直接测量自由衰减信号,只能得到4个分量.分析可知ρ(0)有ρ11,ρ12,ρ13,ρ14,ρ22,ρ23,ρ24,ρ33,ρ34和ρ44共十个独立分量.因此通过一次直接测量并不能对一个未知的量子态进行重构,解决方法是通过引入观测脉冲再进行间接测量.实验上通过一定的观测脉冲集合可完全实现对未知量子态的重构.例如对上面讨论的两比特系统,可以引入观测脉冲集合{II,XX,IX,IY}来完成量子态重构.

3 利用核磁共振实现量子算法

量子计算是利用量子力学原理来实现计算的模型,它利用量子叠加态这一不同于经典计算机的资源,使得其运算速度远快于经典计算机,于是可以用量子计算机来解决一些在经典计算机上不可行的难题.例如,使用最好的经典算法来质因数分解一个n位的整数需要Θ(exp(n1/3log2/3n))次操作.然而,用Shor提出的量子算法完成同样的任务只需要Θ(n2lognloglogn)次操作[65].也就是说,运用量子算法进行质因数分解相比于经典算法可以实现指数加速.目前在很多量子计算平台都已成功地演示了Shor算法[66−70].考虑退相干效应,此时第k个核的系综平均测量信号为

其中Vk0是初始信号强度,是第k个核的横向弛豫时间.以两比特的测量为例:

本文简单介绍求解线性方程组的Horrow-Hassidim-Lioyd(HHL)算法、与机器学习有关的量子支持向量机(SVM)算法、可以实现非酉操作的对偶量子算法,以及这些算法在核磁共振系统上的实现.

3.1 HHL算法

线性方程组的求解问题在科学和工程领域都起着极其重要的作用.例如在导航系统中终端接受到N个卫星的信号去定位一辆汽车的位置,然后通过地理位置关系和数学变换得到一个(N−1)维的线性方程组,求解该方程便可以得到车辆的位置信息.杜江峰研究研究组[33]第一次利用核磁共振系统成功的演示了HHL算法.对于经典计算机求解N个未知数的线性方程组,即使得到一个近似的解,一般来说需要的时间与未知数的个数N成正比.Harrow等提出的HHL算法解一个N维的线性方程组的速度与O(logN)成正比,与经典算法对比实现了指数加速的效果[71].值得一提的是,最近的量子算法普遍采用了酉算子的线性组合来的对偶量子计算范式[72].已证明,HHL算法可通过计算范式的酉算子线性组合的方式来构造[73].HHL算法的细节如下.

这样定义保证了A′的厄米性[74],我们可以在量子处理器上求解线性方程组(18)进而得到它的解x.在下面的讨论中假定A是厄米的.如图4所示,本算法为了进行相位估计引进量子寄存器c,为了投影测量又增加了一个辅助比特.量子寄存器b为工作比特,将向量b编码在这个比特上,同时最后的解向量x也在这个比特上输出.

这个算法中最主要的有两点.首先,使用相位估计算法,选择受控酉门为eiAτt0/T,其中 T=2l,t0=O(κ/ε),l 为量子寄存器c所需的量子位数量.完成步骤1后得到的量子寄存器c和b的量子态是以矩阵A的本征矢量为表象的量子态:其次, 增加一个辅助比特用作为控制位,通过受控旋转门来得到最终量子态:

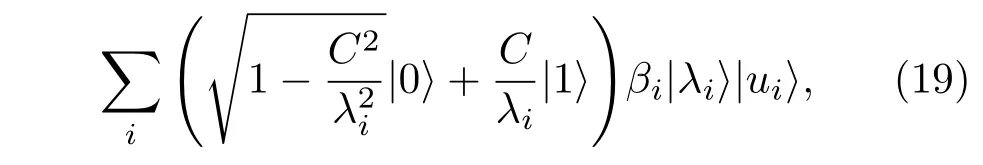
选择一个适当的常数C来满足归一化条件.为了实现这样一个态,首先制备态其中 θi=2arcsin(C/λi) 从态开始,态来控制辅助比特旋转.最后,进行相位估计的逆过程得到

图4 核磁共振实现HHL算法量√子线路图 其中r=2,t0=2π;单比特操作S和H是相移门和Hadmard门,S=(1 0;0 i),H=(1 1;1 −1)/;R(θ) 是绕 y 轴的旋转操作,R(θ)=(cos(θ/2) − sin(θ/2);sin(θ/2)cos(θ/2)),带有×的竖线代表交换门Fig.4.The quantum circuit of nuclear magnetic resonance(NMR)realizing HHL algorithm,where r=2,t0=√2π.The single-qubit operations S and H are phase-shift gates and Hardmard gates.S=(1 0;0 i),H=(1 1;1−1)/R(θ)is a rotation around y axis.R(θ)=(cos(θ/2) −sin(θ/2);sin(θ/2)cos(θ/2)).The vertical line with × represents the exchange gate.

关于实验方面的进展,Pan等[33]用核磁共振量子处理器演示了该算法.选择溶解在氘代氯仿中的碘三氟乙烯作为4比特样品,其中13C核和三个19F核组成一个4比特系统.实验主要分为3个步骤:首先把系统制备到有效纯态(PPS).然后对第三个量子位进行绕y轴旋转θ角度旋转操作,得到初态归一化的状态最后,在初态ρ0之上实现如图4的量子线路.

在实验中,他们选取一个特殊的矩阵A:所有的操作都通过梯度上升算法优化的脉冲序列来实现.最后进行单量子比特的态重构,从末态读出目标态|x.这是首次在核磁共振量子处理器上实现解线性方程组的量子算法的演示.

3.2 量子机器学习

人工智能和机器学习的研究一浪高过一浪.然而在经典计算机上,这些算法需要大量的资源支持[75].伴随着量子信息技术的发展,人们可以试图利用量子并行性来构造量子机器学习算法,来解决这些问题,与经典机器学习算法相比,有的量子算法甚至是可以接近指数加速[76,77].量子计算机的产生从某些层面上也推动了经典机器学习的发展.运用量子力学的原理可以优化经典的机器学习算法[78−80].

量子信息和机器学习的交叉领域无论理论还是实验上都取得了一些进展[81−84],其中之一就是实验上演示了量子版本的支持向量机算法.支持向量机算法是监督学习的一种,通过运用标准数据的训练,可以对未知数据进行分类,解决的是二元分类问题[83].Li等[84]运用支持向量机解决图像识别问题,展示了这种算法可以学习标准集的特征,然后从两个备选答案中识别图像的特征.作者利用打印的标准字体‘6’和‘9’来训练机器,然后让机器识别手写的‘6’和‘9’. 具体来说,首先数学处理图片转化为向量,包括垂直比和水平比.其中垂直比由垂直方向上半部分的像素点总和除以下半部分的像素点总和；同样的水平比是水平方向左半部分像素点总和除以右半部分总和.计算标准字体‘6’的打印图片可得其向量为x1=(0.987,0.159),计算标准字体‘9’可得代表它的向量为x2=(0.354,0.935).同样的手写的字体也要经过这样的数学处理.文中作者定义字体‘6’为一类,用y=1表示,为正类；字体‘9’为一类,用y=−1表示,为负类.而支持向量机算法就是通过对已知标记结果的数据进行训练,然后对一个新的向量x0进行二元分类.

在数学上,存在一个超平面,定义为:w·x+b=0.而正类中所有数据满足w·x+b>1,负类中所有数据满足w·x+b 6 1.那么接下来支持向量机算法中最核心的一个最优化的问题:在满足yi(w·x+b)>1的条件下,通过求解w和b来实现最优超平面(两类之间的距离最大).在最后求得超平面的参数得到的情况下,对一个新向量x0进行分类,计算结果由下式得到:如果y(x0)=+1,我们把这个新向量归到正类,这就是这个向量代表的手写字是‘6’.如果y(x0)=−1,就把这个新向量归到负类,也就是这个向量代表的手写字是‘9’.在支持向量机算法中,向量w可以表示为其中M为训练的数据量,αi是第i个训练数据xi的权重.因此,求解αi和b来实现最优化超平面.根据支持向量机的最小二乘法近似[85],这些参数可以由求解方程得到:

3.3 对偶量子计算

回顾已有的量子算法都是使用酉操作的乘积,酉算符的逆算符也是酉算符,因此过去的量子算法都是通过酉算符的乘或除进行的.因此经典算法中的许多操作都无法在量子算法中直接运用,如加减乘除及其线性组合.量子算法操作的幺正性严重限制了量子算法的发展.如果能够利用酉算符的线性叠加来构造量子算法,则可以吸纳很多经典算法的很多技巧.

利用酉算符线性叠加来进行量子计算的对偶量子计算算法在2002年提出[72],随后得到了飞速的发展[86−103].这种新的计算模式采用了辅助比特,在整个量子体系和辅助比特所构成的系统中演化是酉的,但在量子计算子空间中,演化不再是酉的.其数学理论框架在Gudder,杜鸿科,曹怀信以及龙桂鲁的努力下已经趋于成熟.

近年来量子算法取得了重要的进展.线性方程组求解算法[73]、封闭量子体系的新型模拟算法,以及开放量子体系的模拟算法[104]等新量子算法本质上都是利用了酉算符线性叠加的对偶量子算法.

不同于传统的量子计算方法,如图5所示,对偶量子计算是利用量子力学中的波粒二象性,可以理解为对通过不同狭缝的波函数进行平行操作实现非酉演化的操作.在对偶量子计算机中,波函数被分为若干个子波并使其通过不同的路径,在不同的路径中施加不同的量子门操作,然后这些子波重新干涉,给出计算结果.

对偶量子计算整个过程分为四个步骤.考虑一个由工作系统|ψ和辅助系统|0⊗n构成的对偶量子计算系统,其中d=2n为工作系统中需要线性叠加酉算符个数,量子线路如图6所示.

图5 三狭缝对偶量子计算演示图,由一条狭缝注入光波,再由中间的3个狭缝分为3个子波,中间屏后对不同的子波进行不同的操作,对偶量子计算的输出从右边的3个狭缝获得,不同狭缝处的输出对应着不同的量子计算结果[104]Fig.5.Three slits dual quantum computation diagram.The light waves begin with one slit,and then it is divided into three sub-wave with three slits,the middle of the screen after the different wavelets for different operations.The output of the dual quantum computation is obtained from the three slits on the right,and the outputs at the different slits correspond to different quantum computation results[104].

图6 输出的对偶量子计算线路图,|ψ⟩是工作比特初态,|0⟩是辅助比特初态[104]Fig.6.Multi-output dual quantum circuit diagram.|ψ⟩is the working bit initial state,and|0⟩is the auxiliary bit initial state[104].

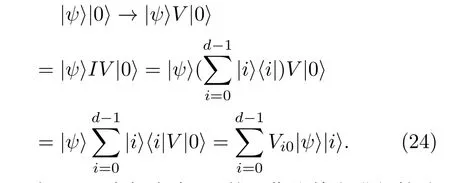
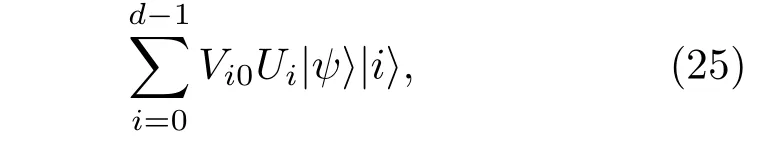
步骤4 在步骤3之后,辅助比特处于叠加态,首先进行振幅放大操作,然后经过测量得到系统输出态.

需要特别指出,当用对偶量子算法来构造闭合系统的动力学演化过程时,如果不进行振幅放大,算法是有成功概率的.算法的成功概率Ps对应着辅助比特处于|0态的概率.计算可得:

失败概率为

举个具体例子来说,我们可以利用对偶量子算法模拟开放量子系统.由于和环境不可避免的耦合作用,几乎所有现实的量子系统都是开放量子体系.开放量子体系的演化通常是非幺正的,因此也适合使用对偶量子计算模式进行模拟[104],量子线路如图7所示.开放量子体系的时间演化可以通过Kraus算子来实现,而Kraus算子可以表示为幺正算符线性叠加的形式.我们通过实现Kraus算子的方式给出了一种模拟开放量子体系演化的对偶量子算法,这种算法相比较于传统的幺正算法有两个优势.首先,算法的询问复杂度由原来的维度的四次方量级O(d4)降低到三次方量级O(d3).第二,通过使用泰勒展开截断近似的方法,相较于以前的幺正模拟算法精度有了指数级提高.

我们考虑一个与单比特环境耦合的单比特工作系统.U是作用在工作比特和环境上的算符[104].U表示为

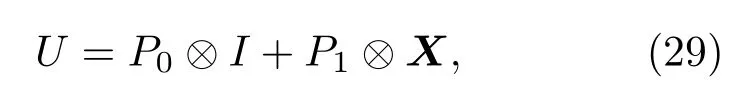
其中X是表示作用在环境上的泡利矩阵,P0=作用在工作系统的投影算符.环境的初态为在这种特殊情况下,Kraus算子的数目为2.演化方程为

其中E0=P0,E1=P1,并满足完备条件:

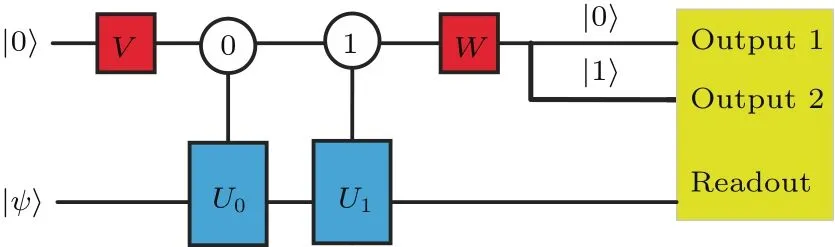
图7 实现单比特开放量子体系演化的线路图,其中V,W 是正文中提到的合波、分波算符,U1,U2在下文中有详细叙述Fig.7. The quantum circuit of the evolution of a single-qubit open quantum system. Where V and W are the combined wave and split wave operators.U1,U2are described in detail below.

E0和E1可以分别由对偶量子门 L0=实现.将E0和E1分解为如下形式:

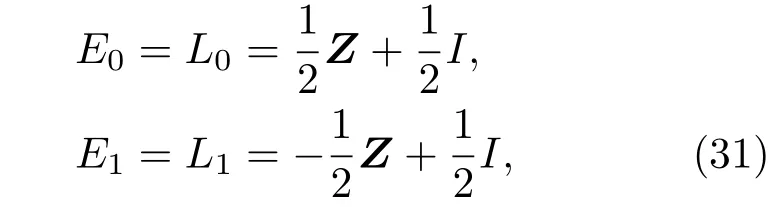
其中Z是泡利矩阵,U0=Z,U1=I.幺正算符V和W可以选定为

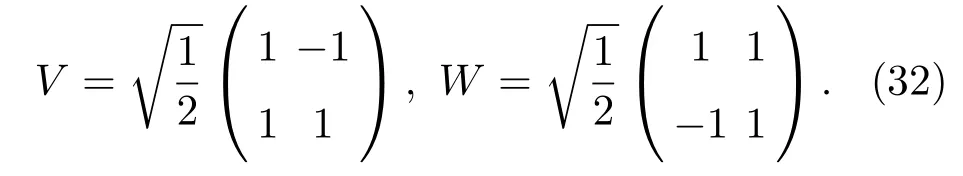
在获得U0和U1对应的哈密顿量后,可以通过泰勒展开截断近似的方法在对偶量子计算里实现哈密顿量的近似模拟.

另外基于对偶量子计算对量子通道的模拟已由Wei等[105]在核磁共振平台实现.

4 利用核磁共振实现量子模拟

从20世纪80年代开始,人们逐渐意识到:由于真实的世界是遵循量子力学的,需要利用希尔伯特空间来描述.那么随着系统规模的增加,利用传统的方法来模拟真实物理过程将变得非常困难.一个最直接的困难就是,利用经典的方法模拟系统维度会随着真实系统规模的增加而成指数增加,需要的参数个数将会成指数增加,那么用到的经典计算机的存储资源也将成指数增加.这可能会超越经典计算机的存储能力,而且经典的CPU也不能对如此大的数据量进行处理.由于经典计算机无法有效地模拟量子系统,1982年费曼曾经提出过用量子系统来模拟真实的物理现象[2],这也被认为是量子计算机概念的起源.1996年,Lloyd进一步提出量子计算机可以作为通用量子模拟器对真实系统进行模拟.在实际情况中,针对特定问题的模拟往往可以采用专用量子模拟器来处理[106],并不一定由通用量子模拟器(量子计算机)来实现.

实现所谓的“量子霸权”可以看作量子计算领域的一块里程碑.“量子霸权”,即量子器件在某种实现上可以超越经典超级计算机.量子模拟器则被认为是具有特定目标性的量子计算机,在将来几年可能会触及一些“量子霸权”.这也是实现通用量子计算机的第一步,最近的一些实验已经揭开了序幕.量子模拟器已经成功地在多个量子平台实现,比如离子阱、光学系统和超导系统,还有我们熟知的核磁共振系统[107].核磁共振系统距今也已经历了六十年的发展,其量子控制技术目前可以达到对12量子比特的样品进行精确控制.液态核磁共振量子信息处理首先在理论上分别独立由Cory,Gershenfeld和Chuang在1997年提出.由于退相干时间长且射频脉冲控制精确,往往被认为是一个优秀的量子模拟平台.从2004年起,在核磁共振平台上展示了一系列关于模拟其他物理系统的实验[108−110].2004年,张竞夫等[111]使用三量子比特核磁共振量子系统,实现了基于量子相位估计的量子时钟同步算法.Zhang等[112]在2008年研究了量子临界点的相变,并通过开发量子探针技术使核磁共振系统可以实现更复杂的模拟.2009年,Peng等[39]模拟了具有两体和三体相互作用的哈密顿量,他们利用哈密顿量的绝热演化制备了基态,开辟了在核磁共振系统中模拟复杂哈密顿量的新方法.2010年,Du等[113]在核磁共振系统对一个氢分子进行了模拟,最后得到了基态能量,展示了量子模拟在计算量子化学领域的巨大潜力.同年,退相干引起的局域化效应也被Suter等[114]模拟.2013年,Feng等[40]在核磁共振平台利用数字量子模拟算法对一维空间中粒子在双势阱中的隧穿现象进行了模拟.近期,有很多与生物和量子信息处理相关的交叉方向,而核磁共振量子模拟器甚至可以用来研究一些生物学行为[115,116].

本文将详细介绍单粒子隧穿现象的量子模拟,以及目前NMR量子模拟的两个热点方向:拓扑结构[117,118]和高能物理[119,120].

4.1 隧穿现象的量子模拟

在量子力学的体系里,量子隧穿现象是指如电子等微观粒子能够穿过势垒能量高于自身总能量的一种量子行为.而经典力学里,这是不可能发生的,但是在量子理论中却可以概率性地发生.作为一种基本而重要的量子现象,量子隧穿在很多量子效应中都有着非常重要的应用,例如原子核的α衰变中的隧穿[121],超导库珀对中的隧穿[122].另外量子隧穿还广泛应用于各种现代实验器件,例如扫描隧道显微镜、约瑟夫森结[123].因此对量子隧穿这一基本的现象的模拟无疑有着重要的意义.

考虑一个在囚禁在一维双势阱中运动的微观粒子,其运动规律遵循薛定谔(Schrödinger)方程,

为方便讨论,在这里选取自然单位制,即~等于1,其中ˆP和ˆX分别是量子力学中的动量和坐标算符,为势阱中粒子的哈密顿量.因此,系统波函数随时间的演化如下:

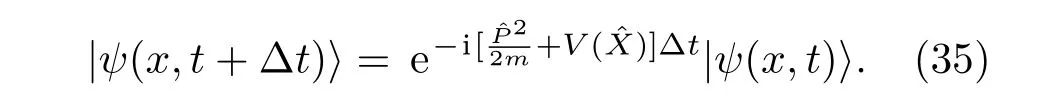
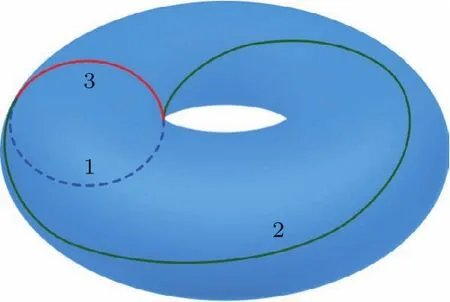
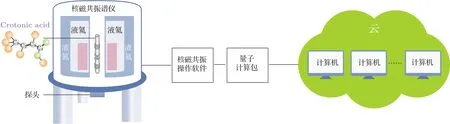
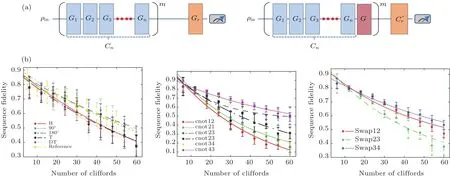
一般而言,粒子波函数在一维空间内是连续分布的,若要对此进行有效模拟,必须把连续的一维空间离散化.Zalka[124]和Wiesner[125]提出了一个算法,假设ψ(x,t)在一维空间是周期分布的,因此只考虑0

其中xk=(k+1/2)∆l,∆l=1/2n,而|k的二进制展开对应的是n比特量子寄存器的基矢.那么接下来的任务就是把(35)式中的动量算符ˆP和势能算符V(ˆX)进行离散化,并在上述基矢下展开.很显然的是势能算符V(ˆX)是坐标ˆX的一个函数,所以V(ˆX)离散化之后在坐标表象下的矩阵形式是对角的[126],某个对角元的数值对应于V(ˆX)离散化后在该坐标下的势能值.同样的方法来考虑动量算符:因为动量算符在自身表象下是对角化的,所以首先我们从它在动量表象下的矩阵形式出发,通过量子傅里叶变换(QFT)得到坐标表象下的矩阵形式.下一步将时间离散化,我们将时间分成许多长度为∆t的时间间隔,然后系统逐步演化,每一步的演化算符U可以由图8来实现.根据Trotter等式[127],

可以把动能和势能算符的同时作用拆成很多个在非常短的时间间隔∆t内动能算符和势能算符相继作用,正如图8所示.在图8中是个三比特系统,对应N=8.其中F是三比特的傅里叶变换算符,F−1是三比特的傅里叶逆变换算符.D是动能演化算符,傅里叶变换会使比特位倒置,所以D=S,S是比特位数倒置算符.Q=是势能演化算符,V(ˆX)在本文中只与第二个比特有关.

图8 对一个步长∆t内的系统演化进行模拟的三比特处理器量子线路图[40] |ψ1⟩,|ψ2⟩和 ψ3 分别是量子处理器的第一个、第二个和第三个比特的输入态波函数,其中F是三比特傅里叶变换算符,F−1是三比特傅里叶逆变换算符,D是动能算符(正文中有详细解释)Fig.8.A three-bit processor quantum circuit diagram simulating the evolution of a system in one step in time of∆t.|ψ1⟩,|ψ2⟩and ψ3are the initial quantum state.F is the three-qubit Fourier transform operator and F−1is the three-qubit inverse Fourier transform operator.D is a kinetic energy operator(explained in detail below)[40].

至此,我们将一维空间中的粒子波函数在空间和时间上都离散化了,而且把作用在波函数上的每一步的U操作也离散化了,拆分成量子计算机可实现的门操作,那么这个过程就可以在一个n比特量子处理器上进行模拟.在本实验中,选择一个三比特核磁样品,也就是N=8,对应于八个基矢:|000,|001,···,|111. 考虑双势阱的每个势阱占据两个格点位置,一个势阱的位置是|010和|011,另一个势阱在位置|110和|111,其他位置是势垒.在本实验中,势阱深度为−V0,势垒高度为V0.利用梯度上升脉冲算法(GRAPE)优化脉冲序列来精确实现每一个时间段的U操作[9].如图9所示,初始时制备粒子在态|110上,或者说粒子处在右边的势阱里.经过几段时间∆t的哈密顿量的演化,最后得到实验结果如图9所示,粒子也有一定的概率处于左边的势阱.所以我们说粒子在两个势阱之间发生了隧穿,而且可以定量地求得隧穿几率.也就是说对于一个把一维空间离散为N个格点的系统,利用量子计算机来模拟只需要log2N个量子比特就可以完成对量子隧穿的有效模拟,这要远小于用经典计算机进行模拟所需要的比特数.因此,可以看到量子计算机和量子模拟的巨大优势以及广泛的应用前景.

图9 利用三比特核磁样品进行模拟双势阱隧穿的实验结果与理论的对比[40] (a)理论分布;(b)实验结果;从左至右依次是粒子在八个格点几率分布随时间的变化,时间取值为0,∆t,2∆t,3∆t,4∆t,5∆tFig.9.The experimental results and theoretical comparison of the dual-well tunneling using a three-bit NMR sample are shown[40]:(a)The theoretical distribution;(b)the experimental results.From left to right,the probability distribution of particles in eight grid points changes with time,and the time value is 0,∆t,2∆t,3∆t,4∆t,5∆t.

4.2 拓扑结构的量子模拟

拓扑量子计算(TQC)作为量子计算体系之一,在2003年由Kitaev提出[118].由于拓扑结构对局部微扰具有鲁棒性,因此拓扑量子计算有望成为实现容错量子计算的一种方法.拓扑量子计算中使用的基本元素是一种二维系统中具有不平庸统计的激发子,被称为任意子.通过在2+1(时间)维时空中编织任意子的世界线实现辫子操作,而拓扑量子计算的酉操作即由这些辫子操作生成.和其他量子计算模型相比,拓扑量子计算具有天然的优势,即局部误差对这些辫子没有影响,因此这种量子计算的体系结构对于小的扰动或错误有极强的抗干扰性.然而,这个有前途的计算架构自从提出以来仍然停留在理论阶段,拓扑量子计算在真实物理系统中仍然没有实现.然而量子模拟器的发展却为我们提供了一种研究拓扑结构的新方法.这样,我们可以运用一个量子体系来研究拓扑结构的问题,而不是建立在一个真实的物理系统中.例如,拓扑阿贝尔和非阿贝尔之间的拓扑序可以被有效地模拟.在众多的科研问题中,有一个问题是如何区分拓扑序.事实上,拓扑序可以由以下三个因素唯一地确定.任意子类型,拓扑性质和受拓扑保护的基态.任意子类型和拓扑保护的基态在圆环上都是等价的,因此标识一个拓扑序只依赖于任意子的拓扑性质:自统计、编织和融合.其中一种常用的方法是研究它们提供的模块化S和T矩阵,其中包涵了任意子拓扑性质的完整信息.如图10,最近我们研究组报道的一个实验表明,可以表征拓扑序,并通过模块化的S和T矩阵来识别它们,这个实验在三量子比特核磁共振量子模拟器上实现[128].在核磁共振实现过程中,用溶解在氘代氯仿溶剂中的13C标记的三氯乙烯(TCE)样品作为一个三比特量子处理器.实验过程分成三个步骤:制备拓扑保护基态、调节控制脉冲驱动样品进行模块化的演化以及进行最后的测量.实验成功模拟了Z2环面编码的状态、双西蒙序和双斐波那契序,而且还可以通过实验结果区分它们.在同一时间,Luo等[129]解决了一个新的问题:“使用最先进的技术究竟可以观察到多少遵守物理原理的拓扑序的细节？”他们的实验样品是1-溴-2,4,5-三氟化苯,由此作为一个5比特的核磁共振量子模拟器.他们在绝热条件下制备了随机基态并测量了模块化的S和T矩阵.他们发现可以通过使用最小输入哈密顿量函数从制备到测量来解决Z2环面编码模型.这是第一个实现拓扑序的实验,并测试了它们在微扰条件下的鲁棒性.这将会开拓一个新的领域,来研究其哈密顿量的拓扑序是否完全可解.

图10 这项工作是模拟环面上的最小蜂窝格,这个圆环只包含一个辫子,两个顶点和三个边,1,2,3分别是可以用三个量子比特来模拟的三条边[128]Fig.10.The work is to simulate the minimal honeycomb lattice on a torus.This torus only contains one plaquette,two vertices,and three edges.1,2,3 are three edges which can be simulated by three qubits respectively[128].

4.3 高能物理的量子模拟

接下来介绍下我们研究组在另一方面的工作:利用核磁共振量子处理器模拟高能物理领域的问题.其他一些量子计算系统已经证明了高能物理的问题可以在量子模拟器上进行模拟[130].核磁共振量子模拟器也有一些高能物理模拟的成果.最近,我们研究组使用核磁共振量子模拟器,测量全息纠缠熵,模拟了反德西特/保形场理论对偶问题(ADS-CFT)[131].

图11 RT公式示意图 (a)锚定到所选边界区域A的最小表面(红线);(b)张量网络态的一个例子.(六边形)节点代表张量.这些连接代表了张量之间的纠缠,而悬腿是多体系统中的物理量子比特.红色虚线弧表示锚定到区域A的虚拟表面S,它的截面将切割一个最小连接数[131]Fig.11.Discription of the RT formula[131].(a)The bulk minimal surface(red line)is anchored at the boundary of the boundary region A.(b)An example of tensor network state.The(hexagon)nodes represent tensors. The links represent the contraction of tensors.The dangling legs are physical DOFs in many-body system.The red dashed curve illustrates the virtual surface S anchored to region A,which cuts a minimal number of links.

在经典的时空观中,物理量是连续的.但是,一些物理量在量子时空中是不对易的.因此,这些曾经是连续的物理量可能现在变得离散.量子时空是对时空概念的一种概括,它是一个新兴的领域,包涵了量子力学和广义相对论.目前主要有两种方法来研究和扩展量子力学或广义相对论.第一种是著名的弦理论,弦理论是通过考虑当前量子场论中的引力来构建的,最终成为有关量子引力的一种理论.其次,作为弦理论的主要竞争者,圈量子引力(LQG)从相对论开始引入,试图增加量子性质.在过去的二十年里,反德西特/保形场理论对偶是其中一个与量子引力理论有关的重要猜想之一.它预言了量子场理论在低维空间,量子引力理论在大的反德西特时空中与保形场理论是等价的.

从边界场理论中的纠缠出发,Li等[131]全面重建了一个空间.为了确定纠缠熵SEE(A),文中引用了Ryu-Takayanagi(RT)公式:

其中GN是牛顿常数,A是(d−1)维的边界区域,具有(d−2)维最小的表面Armin锚定到A.另一方面,最近比较热的领域称为张量网络介绍了一种RT公式的离散化版本,见图11.在这些发展的引导下,量子模拟器可以有效地来模拟这些过程.例如,六比特的核磁共振量子模拟器最近被用来实现这些过程的演示.用溶解在d6-丙酮中的1/2自旋13C标记的13C二氯-环丁酮样品是6比特量子处理器.Li等使用控制技术包括GRAPE和一个脉冲反馈程序以提高射频脉冲的准确性.实验成功演示了等级-6的最小PT的模拟.虽然他们只是实现了RT公式中最小的情况,但他们的结果进一步表明RT公式或反德西特/保形场理论对偶问题可以在一个更大的量子系统上进行模拟.

对量子引力而言,圈量子引力是对量子时空的另一种描述.在LQG的框架中,在某个时间点,几何可以被认为是集中在一维上的结构.它只是一个简化的面向一维的网络,因此被称为自旋网络.Penrose第一次提出导向线连接在一起可以形成一个完整的网络.在自旋网络中,量子时空可以分解成某种量子四面体.这个四面体对应于某个态,也可以在当前量子器件如核磁共振量子模拟器平台上进行模拟[132].另外,如果量子比特数增多,我们可以来模拟它们的动力学演化过程.而且,核磁共振平台也可以用来模拟其他相关的模型,比如被看作是混沌系统中的量子扰码的黑洞[133,134],Sachdev-Ye-Kitaev模型[135]和时空几何涉及的纠缠[136].

5 核磁共振量子云计算平台

基于云的量子计算平台(量子云计算平台)的出现,有望成为大众触手可及的量子计算平台,广大量子信息理论工作者乃至量子计算爱好者可以切身地体验量子计算与经典计算的不同.与平常使用的云服务类似,量子云也是一项云服务,区别在于它的服务器是存放于实验室的量子计算物理系统.来自互联网的用户们可以将想要执行的量子程序远程上传到量子云平台的服务器上,并在真实的量子系统上完成所需执行的程序.IBM公司引领着这个崭新领域:早在2016年5月,他们的超导量子团队便迈出了第一步,发布了5比特超导量子云平台.在随后的一年中,IBM一边积累维护量子系统的经验,一边不断积累用户的反馈数据.在2017年5月他们将超导云平台的量子比特数目由5扩展到了16.

视线转向东方.在2017年10月11日,我们也发布了自己的量子计算云平台(http://nmrcloudq.com/zh-hans/):NMRCloudQ[137].核磁共振量子系统,如前所述,对量子计算的发展发挥了许多重要的作用.基于此系统,我们希望能够在这个瞬息万变的时代,紧跟量子技术变革的步伐,为实现让更多的人能体验量子计算机的目标而努力.这项工作旨在使无论是专家还是新手,都能较好地在该平台上体验量子计算的乐趣.

我们的量子云平台,如图12所示,主要部分是核磁共振谱仪,另外为了与远在云端的用户连接起来,运用一台服务器整合量子计算算法包和核磁共振谱仪操控软件.另外,这台服务器也承担着管理用户和实验任务的使命.我们提供了高保真度的20个单比特操作和9个两比特操作,按照理论,这些操作能够造出任意的4比特门.用户可以登陆我们的网站,按照网页提示,利用这29个量子门构造出自己希望的量子操作,设计4比特以内的量子线路,并提交任务等待实验.一旦实验完成,系统会自动进行完全态重构,我们会提供所有的测量信息作为反馈.

通常来讲,一个量子计算实验往往包含三个部分:初始化、实现量子线路和测量.在核磁共振量子计算中,初始化是通过制备赝纯态来实现的.在我们的云平台中,采用了空间平均法[138]来实现这个过程.通过态重构技术,测得这一赝纯态的保真度达到了98.77%.理论上,任何的量子线路图都可以分解成一系列通用量子门组合的序列.我们在机器中储存了大量事先优化完成的脉冲序列,这些序列包括对四个比特的单比特操作:Hardamard门,90◦和180◦旋转和两类相位门,以及6种控制非门和3种交换门.可以证明,这些门是通用量子门集合的一种选择.通过GRAPE方法,能在4比特的核磁共振系统中找到高保真度的控制脉冲.通过随机检测基准(RB),如图13所示,得到实现这些通用量子门的脉冲序列:单比特操作保真度达到99.10%,两比特保真度达到97.15%.在这之后,我们会统一地对量子线路的结果进行态重构,并将态重构的结果返回给用户.对于用户而言,他们所需的是要确定进行的操作和顺序,并按照网站规则提交控制命令即可.

图12 核磁共振量子云平台各组件连接方式:基于4比特核磁共振量子系统,我们整合核磁共振操控软件和量子计算相关程序,在访问我们的服务器后,外接用户通过基本的量子线路,便可以体验量子计算机这一真实物理系统的运行方式Fig.12.The components of NMR quantum cloud platform:We integrate NMR manipulation software and quantum computing procedures.After accessing our server,the user can experience the real physical system of the 4-qubit quantum computer.

图13 (a)随机基准化(RB)序列图,包括两个子图,其中左图为标准的随机基准序列,它的作用是作为参考,我们重复m次随机构成的n个逻辑门组成的序列,其中逻辑门由Gi表示,并通过一个恢复操作Cr测量出最后系统的保真度,右图则为测量目标门G的随机基准化的序列,其中与标准的随机基准化序列不同的是,在每一次重复n个逻辑门Gi后,所添加的目标门G,同样最后在恢复操作Cr的作用后测出最后系统的保真度;(b)实验结果包括三个图,分别是单比特逻辑门随机基准化结果、控制非门的随机基准化结果和交换门的随机基准化结果,其中横坐标表示随机基准化序列中门序列的个数,纵坐标表示最后测量系统的保真度Fig.13.(a)RB(randomized benchmarking)circuits.The left part is about standard RB as a reference is implemented by constructing a sequence of m random gate set.The right part is that interleaved RB is performed to estimate the error of a specific gates,where is interleaved with random gate set.Final gates and are performed in the end,as the recovery operations.(b)RB results for single-qubit gates,CNOT gates and SWAP gates.The leftfigure single-qubit RB result for the first qubit.The middle figure RB results for CNOT gates and the right one results for SWAP gates.

就未来的发展来看,制约4比特核磁共振量子云平台发展的一个很重要因素是控制脉冲的精准度.平均来看,单比特门的错误率0.90%和两比特门错误率2.85%,并不能算是杰出.实际上,今后可以通过多种技术来提高精度.对于单比特操控,由于误差大多来自磁场的不均匀性和控制脉冲的优化过程,因此可以采取:1)反馈控制技术;2)射频脉冲选择技术;3)提高优化阈值来提高基本逻辑门脉冲的表现.对于两比特操作,由于两比特门脉冲长度过长,退相干成为主要的错误来源.又由于脉冲长度是和比特之间耦合强度成反比的,因此我们希望在今后选取耦合更强的核磁共振样品.这样就能够实现两比特门脉冲长度和目前单比特门脉冲长度相近,从而可以很好地解决退相干的问题.另外,由于目前的4比特样品是将氢原子解耦,在不解耦的状态下,它会拓展成一个七比特的样品.因此也能够将样品自动扩展到七个比特,实现七比特的核磁共振量子云平台.

对比超导体系的量子云平台,我们的系统由于不可拓展性的天生问题,很难在未来发展成实用化的大规模的通用量子计算机.然而,作为最早发展量子计算的平台,核磁共振系统对于环境噪声有很强的抗噪能力,因此我们的量子云平台的逻辑门将会比其他系统表现得更好.而且领先其他平台的是,我们直接提供态重构后的密度矩阵,即能反馈量子实验结果的所有信息.

总之,量子计算云平台对于今后量子计算的发展,无论是推动整个领域的普及还是面向未来量子云平台的发展提供更多可操控的量子位和更精准的控制技术都有很重大的意义.我们的目标是提供一个准确可靠的量子计算物理系统,让大家都能来体验,学习,甚至是进行科学研究.在目前的状态下,也许还存在诸多问题,但我们也希望这项工作不仅能推动核磁共振控制技术的发展,也能在量子云计算方面有重要意义.

6 结 论

作为实现量子信息处理的第一代处理器先驱,相信液态核磁共振仍能在实现未来的通用量子计算机计划中发挥重要的作用.首先,液态核磁共振技术是展示量子信息处理最成功的技术之一.在核磁共振中得到的实验数据可以被其他量子系统参考和使用以精确地实现量子门操作,因此液态核磁共振将成为量子信息处理发展的一个可靠的试验平台.第二,核磁共振是一个可以模拟复杂多体动力学的系统,而其他平台以当前技术实现对这种复杂系统的模拟通常是不可行的.第三,其他潜在的量子处理平台的技术开发需要核磁共振为其提供完善的经验和指导,例如核磁共振系统上开发的高精度的相干量子操作技术,如梯度下降优化算法、量子反馈算法等.虽然有如此多的量子控制技术、理论量子算法和量子模拟方案被成功地在液态核磁共振平台上实现,但核磁共振仍存在一些缺点,诸如不可扩展性、不能重置量子位以及量子门的脉冲时间长等.

此外,以液晶和固体为基础的新一代核磁共振平台还有待于进一步的发展,基于此方法将克服液态核磁共振中现有的许多限制.用于量子信息处理的固态核磁共振将带来四个好处:1)提高极化率,增加灵敏度;2)具有更长的相干时间,利用这一点可以展示更加复杂有趣的算法;3)自旋之间的耦合更强以减少实现量子门操作的时间;4)重置量子位.因此,固态核磁共振提供了一个探索量子信息处理的新领域的机会.

总之,量子计算机有望成为下一代信息处理器,并且一旦实现将有望带给我们比现有的经典计算机更为强大的计算能力.虽然通向构建一个实用化的通用量子计算机的道路是蜿蜒曲折的,但我们相信在许多科学工作者和机械工程师对量子信息领域的努力探索之后,这终将会实现.以近两年的发展来看,我们正接近证明量子优越性,并且在不久的未来,一台量子处理器和经典处理器组成的混合计算机将会成为一个可行的目标.

感谢加拿大R.Laflamme实验组提供的计算GRAPE脉冲的MATLAB程序；感谢北京计算科学研究中心李俊、罗志煌和南方科技大学鲁大为的交流讨论.