一种飞机蒙皮检测机器人曲面运动控制方法

姜俊俊，王从庆，武雪尉

(南京航空航天大学自动化学院，南京 210016)

0 引言

近年来爬壁机器人得到飞速发展，被越来越多地应用于人类生产活动[1-3]，随着它的广泛使用，机器人的结构与控制方式也得到了很大的发展。文献[4]设计了一种仿生可重构的机器人，通过对蝎子的运动机理分析，使得机器人能够完成地面爬行、滚动以及攀爬垂直墙壁的任务；文献[5]设计了一种能够攀爬大型储罐的机器人，该机器人采用磁吸附方式吸附到壁面，且磁吸附位置可以根据不同环境进行调节，使吸附力能够根据不同环境要求进行自适应补偿；文献[6]设计了一种气缸驱动的爬壁机器人，通过对气动系统进行分析，搭建了一个能够实现攀爬平面墙壁的机器人系统；文献[7]设计了一种能够攀爬多孔和粗糙壁面环境的机器人，该机器人的气动系统设计得较为完善；文献[8]设计了一种抽风式的爬壁机器人，机器人有一对驱动轮和一个同轴螺旋桨推进器，能够在斜坡上进行旋转运动和平移运动；为了克服机器人在复杂环境下由于参数的变化造成系统的模型具有不确定性的问题，文献[9-11]提出了一种基于RBF神经网络补偿的控制方式，该控制方式能够自适应地补偿系统不确定性和线性系统残差导致的输出扰动；文献[12]针对刚性机器人操纵器，提出了一种鲁棒自适应滑模跟踪控制方案，自适应RBF神经网络用于学习系统不确定性的上界，然后将神经网络的输出用作补偿参数，从而消除系统不确定性的影响，并且可以使闭环机器人控制系统的渐近误差收敛；文献[13]设计了一种能够在柔软表面爬行的机器人，并且设计了一系列的控制算法，包括具有积分作用的滑模控制器、线性二次调节器(LQR)和用于半自主导航的航位推算。

本文所描述的飞机蒙皮健康检测机器人是一种能够攀爬到飞机蒙皮外表面，通过自身携带的蒙皮健康检测装置，对飞机蒙皮进行实时的健康分析。本文根据双框架飞机蒙皮健康检测机器人运动控制中存在的建模误差、摩擦以及外界干扰，提出了基于RBF神经网络自适应补偿的滑模控制方法，实现了具有不确定性的机器人轨迹跟踪控制；此外，通过使用双曲正切滑模函数消除了普通切换滑模函数带来的系统颤振，最后仿真结果证明了该控制方法的有效性。

通过本文设计的控制器，可以有效解决飞机蒙皮检测机器人在飞机蒙皮外表面单步运动时的轨迹跟踪问题，从而使机器人沿着期望的运动轨迹运动。

1 飞机蒙皮健康检测机器人结构与运动步态分析

1.1 机器人结构

本文所研究的双框架飞机蒙皮健康检测机器人如图1所示。

图1 双框架飞机蒙皮健康检测机器人Fig.1 Aircraft skin inspection robot with double frames

双框架飞机蒙皮健康检测机器人共有4层框架结构，第1层和第4层框架分别为机器人的外框架和内框架，其中，外框架和内框架的中心安装有伺服电机和减速器，使两框架能够产生转动。检测过程描述为：外框架的转动电机用来驱动内框架转动运动，内框架安装的转动电机用来驱动外框架转动运动。第2层框架为机器人实现俯仰姿态调节的机构，目的是使机器人运动过程中能够自适应飞机蒙皮表面曲率。第3层为机器人运动的滑动层，通过滑动电机的旋转带动滚珠丝杠驱动滑动层产生平移运动。通过中心轴将第1层框架与第2层俯仰调节机构连接，实现第1、第2层与第3、第4层的相对转动和俯仰运动，通过滑动轨道将第2层机构与第4层框架连接，实现第1、第2层以及第3层与第4层的相对滑动。

内外框架分别安装4条由气缸组成的机械腿，并且腿部连接真空吸盘，可以使机器人吸附在飞机蒙皮表面，从而实现移动。

1.2 机器人运动步态分析

飞机蒙皮健康检测机器人采用的是双框架结构，当机器人在飞机外表面进行蒙皮健康检测作业时，双框架交替运动，带动机器人平台向前运动。由于飞机蒙皮为一个曲面环境，因此在双框架发生相对运动的同时，机器人俯仰姿态也应该做出相应的调整，以适应飞机蒙皮的曲率。滑动步态包括前向直线移动和俯仰姿态的微调，具体的过程如图2所示。

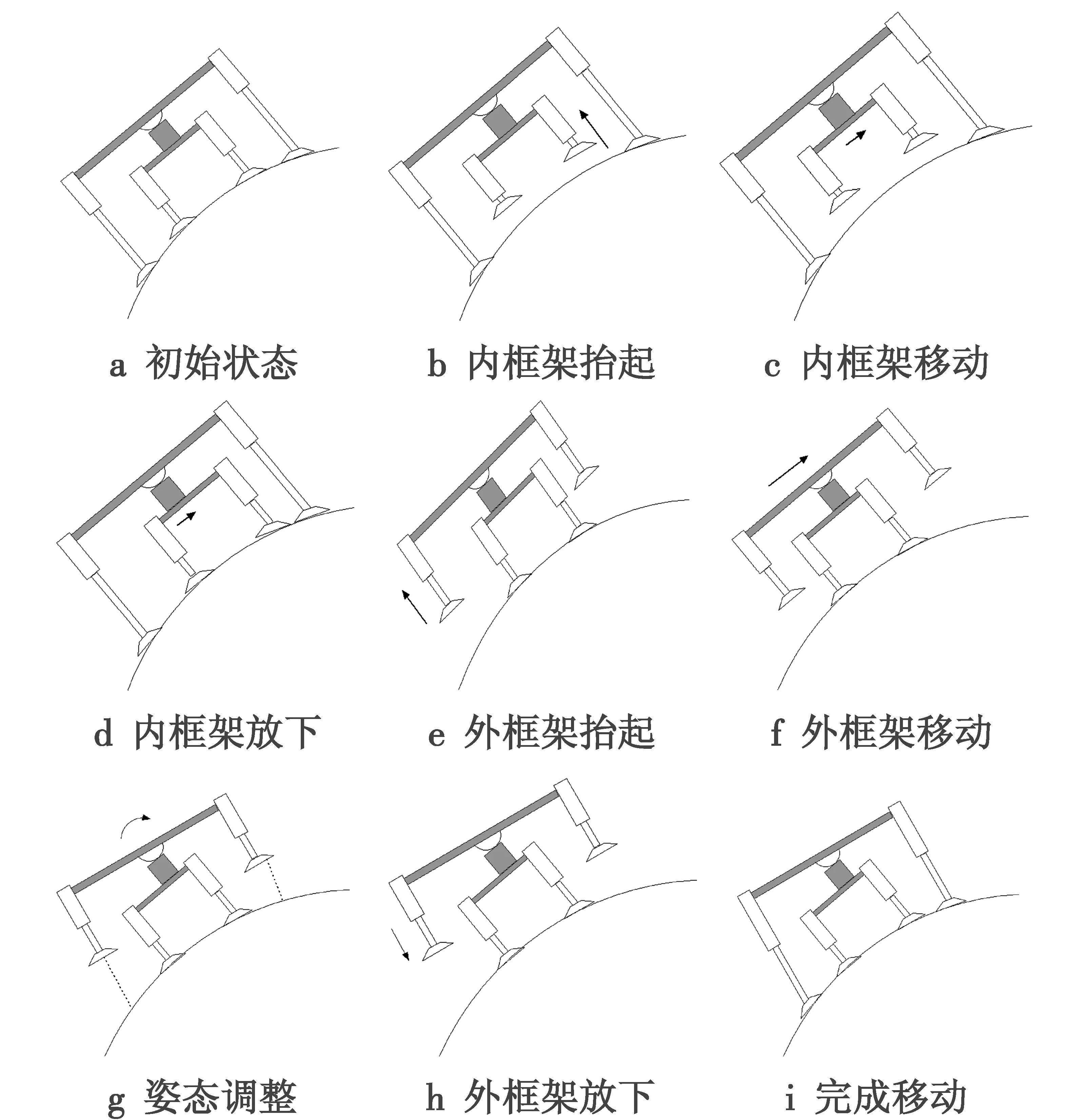
图2 机器人滑动步态Fig.2 Robot sliding gaits

如图3所示，旋转步态大致过程可以描述为：1)初始状态，机器人内外框架均吸附在飞机蒙皮表面；2)外框架吸盘组释放，腿部气缸抬起，旋转一定角度；3)外框架机械腿放下并且吸盘组与飞机蒙皮表面吸附；4)内框架吸盘组释放，腿部气缸抬起，旋转一定角度。

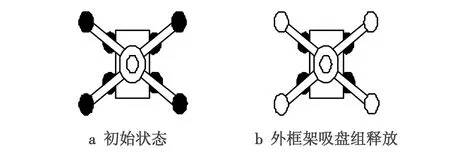
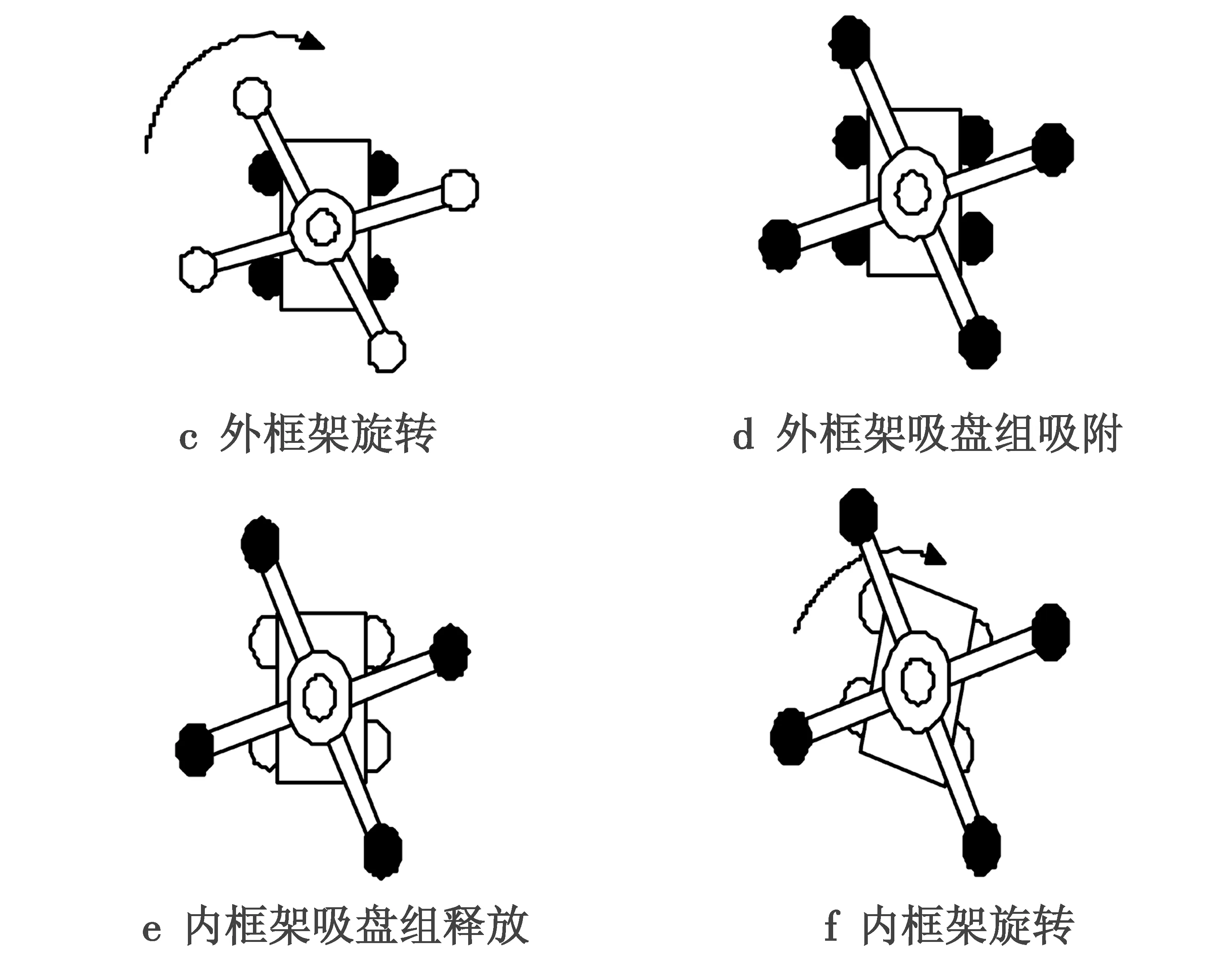
注：黑色表示吸盘组吸附，白色表示吸盘组释放。

图3 机器人旋转步态

Fig.3 Robot rotational gaits

2 飞机蒙皮健康检测机器人动力学建模

图4所示为机器人受力分析简化图。

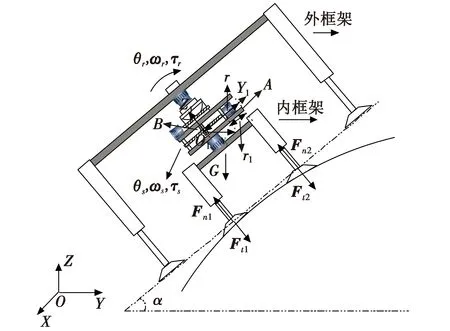
图4 机器人受力分析简化图Fig.4 Simplified diagram of force analysis for robot

由图4可知，机器人在飞机蒙皮上的单步运动过程可以简化为在倾角为α的斜面上运动，下面将具体讨论机器人在该斜面上的运动。

全局坐标系的原点O在地面上，O1选择在B点，G是机器人整体所受的重力大小；B点为转动轴与滑动轴的交点。由于内外框架运动过程类似，本文只讨论内框架的运动过程。选择运动内框架中A点为机器人运动过程中位置和速度的参考点。r为A点移动过程中与外框架转动电机轴之间的水平距离，r1为A点到滚珠丝杠固定端的距离；τs为滑动电机作用在滚珠丝杠上的扭转力矩；ωs是电机带动滚珠丝杠转动角速度；θs为滚珠丝杠转动角度，滚珠丝杠的转动带动滑动层的水平移动；τr为转动电机产生的旋转力矩；ωr为转动角速度；θr为转动轴转动的角度，即为滑动轴逆时针绕转动轴转动的角度，也是滑动轴与Y1之间的夹角。Fn1,Fn2，Ft1,Ft 2分别是与飞机蒙皮接触的上下两组吸盘中每个吸盘所受到的支撑力和吸盘产生的吸附力。

运动内框架中参考点A点的初始位置在r=r1处；将图4中子框架在倾角α的斜面上运动看作是绕转动轴转动和沿移动轴平移运动的耦合，简化为运动的刚体模型，如图5所示。

图5 简化的动力学模型Fig.5 Simplified dynamic model

2.1 基于机器人运动关节的动力学模型

假设运动的内框架总转动惯量为I,滑动运动刚体质量(即内框架总质量，包括内框架电机的质量和内框架的质量)为m1，滑动总距离为l，根据转动惯量计算方法可得

(1)

式中：y1为内框架水平滑动距离；ρ为刚体移动时等效质量线密度，满足

m1=ρl。

(2)

由拉格朗日公式导出动力学模型的过程如下所述。

运动子框架动能为

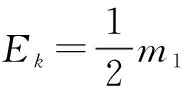
(3)

式中，r=kθs，k为滚珠丝杠的导程。

运动子框架势能为

Ep=m1g(kθs-r1)sinαcosθ

(4)

则系统的拉格朗日函数为

L=Ek-Ep=

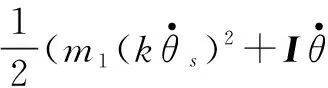
(5)

由

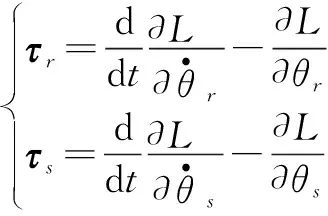
(6)

得运动子框架动力学方程为

(7)

将式(7)写为

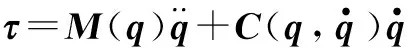
(8)

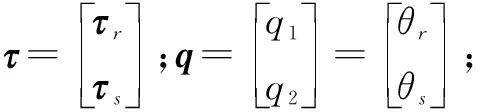
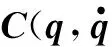
为了使爬壁机器人能够跟踪空间中的某一个设定的运动轨迹，需要建立工作空间参考点的位置动力学模型，并通过设计加在参考点的虚拟控制力Fx，使参考点沿着期望轨迹运动。通过Fx与τ之间的映射关系，求出实际需要的控制力τ。

2.2 机器人在笛卡尔坐标系下的位置动力学模型

以O1坐标系为建立机器人位置动力学模型的参考坐标系，依然以A点为机器人运动过程中的位置参考点，则A点在O1坐标系中的位置可表示为

(9)

由式(9)可得

(10)

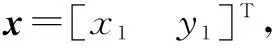
(11)

式中,J(q)是由机构性质决定的，表示一种映射关系，假定J(q)在机器人运动过程中是非奇异的。

在静态平衡状态下，传递到参考点A的力Fx与τ之间存在线性映射关系，即

Fx=J-T(q)τ

(12)

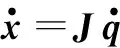
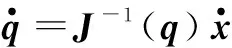
(13)

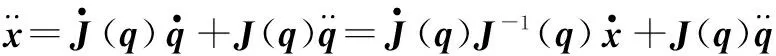
(14)

由式(13)可得

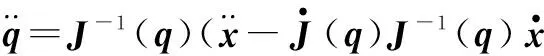
(15)

将式(13)、式(15)代入式(8)可得

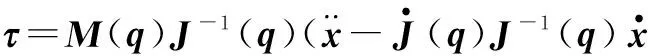
(16)

整理式(16)可得

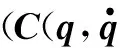
(17)

将式(16)两边同乘J-T(q)可得

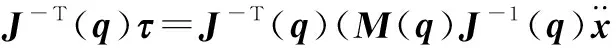
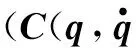
(18)

结合式(12)，同时考虑干扰，得到如下的位置动力学关系式

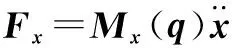
(19)

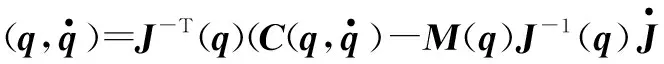
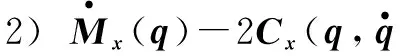
3 基于RBF补偿的滑模控制器设计

假设xd是机器人期望的运动轨迹，x为机器人实际所在位置，定义轨迹跟踪误差为

e(t)=xd(t)-x(t)

(20)

取滑模面[14]为

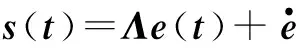
(21)

式中，Λ=diag[a1,a2]>0,为正定对角阵。

则

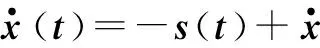
(22)

那么

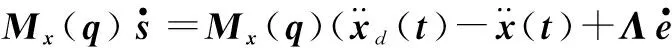
(23)

式中,

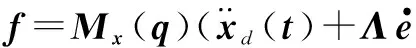
(24)

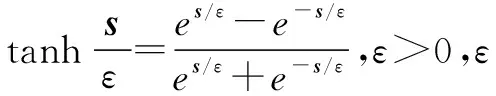
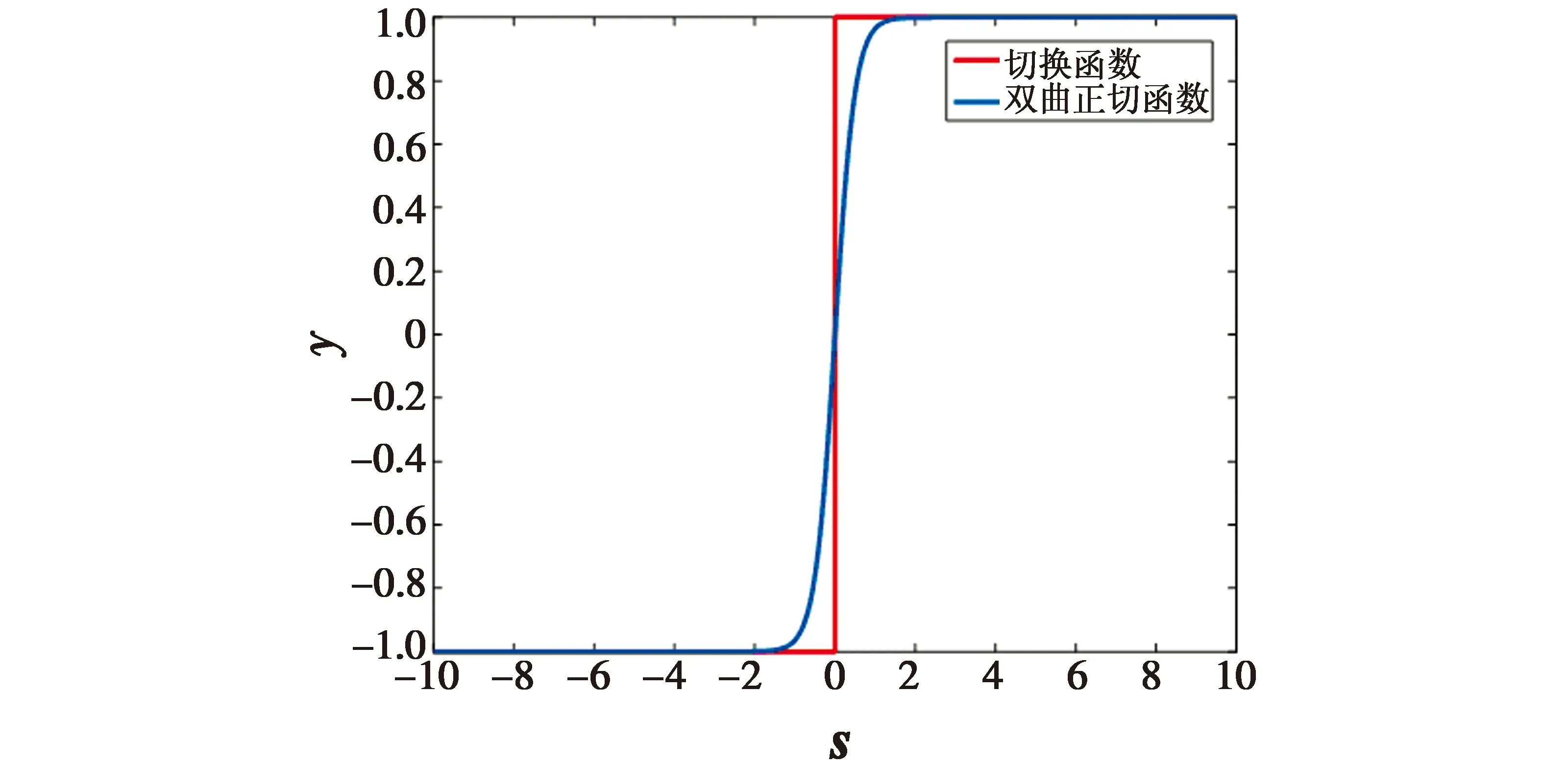
图6 切换函数和双曲正切函数Fig.6 Switching function and hyperbolic tangent function

设计控制率为

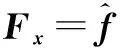
(25)

(26)

神经网络实际输出为

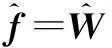
(27)

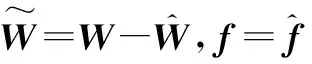
神经网络的结构如图7所示，神经网络权值W通过Lyapunov稳定性理论设计出自适应律在线调整。

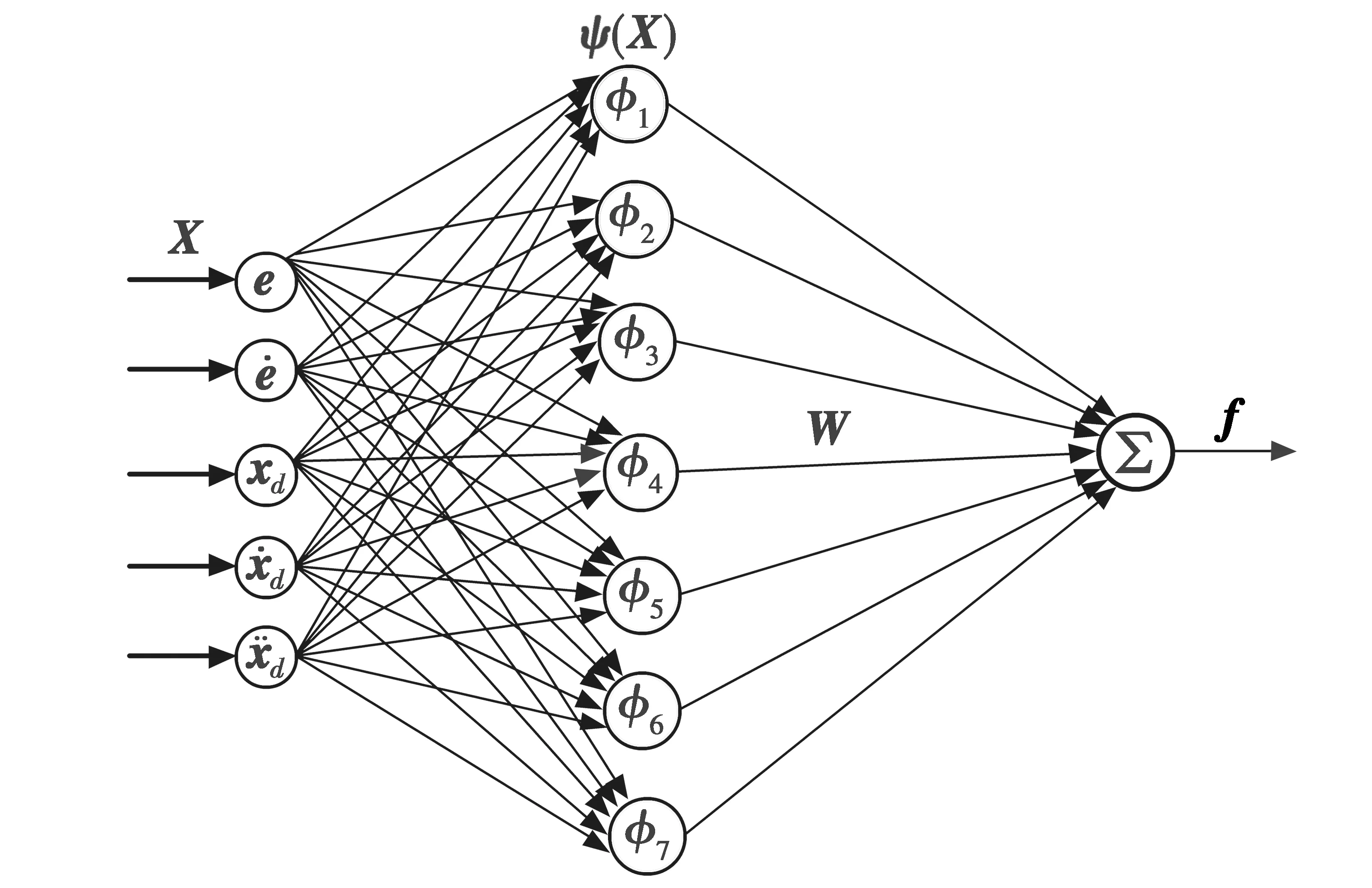
图7 RBF神经网络的结构Fig.7 Structure of RBF neural network

控制律设计为

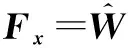
(28)

式中，v=-(εn+bd)sgn(s)是为了克服RBF神经网络的逼近误差εf以及外部干扰力矩τd而设计的鲁棒项，其中，εn，bd分别为εf和τd的上界最大值。

将控制律式(28)代入式(23)可得

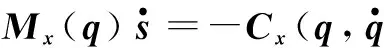
(29)

定义Lyapunov函数为

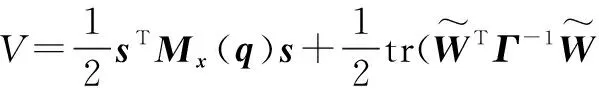
(30)

对式(30)求导可得

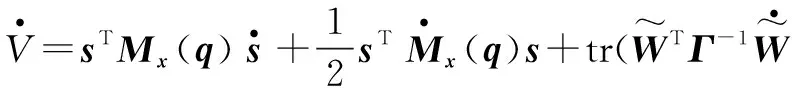
(31)

由性质2可得

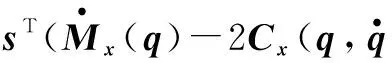
(32)

那么

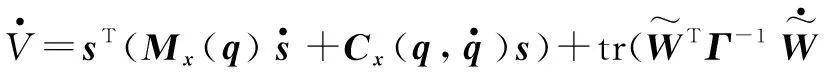
(33)

选取神经网络自适应律为

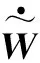
(34)

式(33)结合式(34)化简为

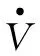
sT(-(εn+bd)sgn(s)+εf+τd)+sT(-Kvs-ηtanh(s/ε))=
sT(εf+τd)-‖s‖1(εn+bd)+sT(-Kvs-ηtanh(s/ε))

(35)

式中，选择εn，bd为εf，τd的上界最大值。那么式(35)结合双曲正切滑模函数的性质可化简为

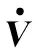
(36)

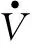
4 仿真分析

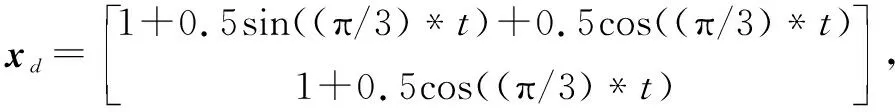
仿真结果如图8～图12所示。

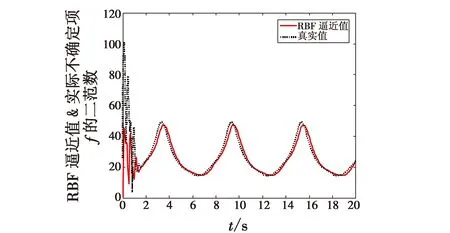
图8 RBF逼近值‖与真实值‖f‖

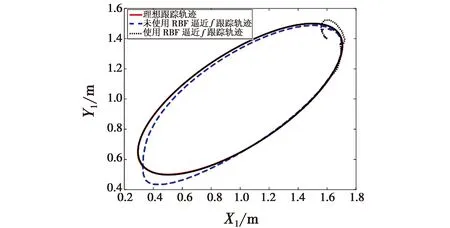
图9 轨迹跟踪Fig.9 Trajectory tracking of inspection robot

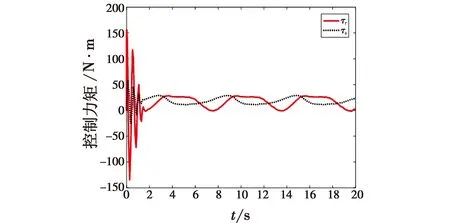
图10 使用双曲正切滑模函数时的控制力矩τr,τsFig.10 Control torque τr，τs with hyperbolic tangent sliding mode functions

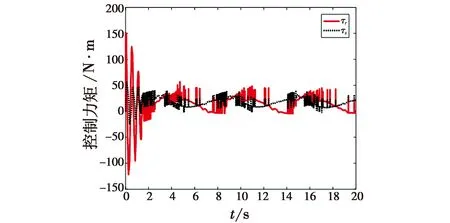
图11 使用切换滑模函数时的控制力矩τr,τs

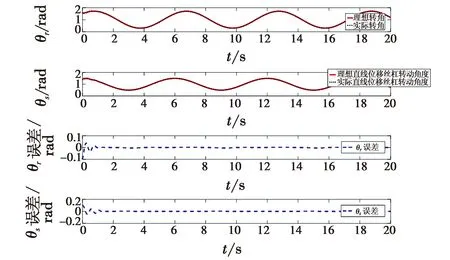
图12 位置跟踪状态及误差Fig.12 Position tracking status and error

从图8可以看出，RBF神经网络可以对系统的干扰项和不确定项进行有效跟踪。从图9可以看出，使用RBF补偿的控制器可以对含有不确定项和干扰项的系统进行有效的轨迹跟踪，未使用RBF补偿的控制器对期望轨迹跟踪的误差较大。图10～图11显示的是在RBF神经网络的补偿下，使用不同的滑模函数时系统的控制力矩变化曲线。通过图10和图11的对比可以看出,使用双曲正切滑模函数可以有效地避免因为使用普通切换滑模函数带来的输入振颤问题。图12显示了系统位置跟踪状态和误差，从误差变化曲线上来看，本文设计的控制器能够对期望运动轨迹进行有效跟踪。

5 结论

本文针对一种双框架飞机蒙皮检测机器人的运动控制问题，首先分析了该机器人的机械结构以及运动步态，建立了机器人动力学模型。其次，针对机器人单步运动的轨迹跟踪控制问题，设计了一种基于RBF自适应补偿的滑模控制器，通过使用双曲正切滑模函数，避免使用普通切换滑模函数带来的抖振问题。最后，Matlab仿真分析表明了RBF神经网络能够有效地对系统中存在的不确定性进行补偿，以及所设计的轨迹跟踪控制律能够完成机器人单步运动的轨迹跟踪控制。