结合正样本集的核相关滤波跟踪算法
2018-12-17刘伟,黄山
刘 伟,黄 山
(四川大学,成都 610065)
0 引言
目标跟踪技术是计算机视觉领域的重要研究课题,其在智能视频监控、人机交互、机器人视觉导航、虚拟现实以及医学诊断等诸多方面均有广泛的应用前景[1-3]。但在实际的场景中,视频中的噪声、目标尺度变化、目标形变、遮挡、光照变化等问题的存在,会严重影响目标跟踪的准确性,设计一个具有精确性、快速性的目标跟踪算法仍然是非常困难的。为解决这些问题,各种跟踪算法相继被提出。目标跟踪算法通常可分为生成式和判别式[4]两类。其中,生成式跟踪算法是不断地去搜索与目标最相似的区域,不依赖目标模型。如文献[5]提出的时空上下文视觉跟踪(Fast Tracking via Spatio-Temporal Context Learning,STC)算法,该算法通过贝叶斯框架对要跟踪的目标及其局部上下文区域的时空关系进行建模,得到目标和其周围区域低级特征的统计相关性。然后综合这个时空关系和生物视觉系统来评估新的一帧中目标出现位置的置信图,置信最大的位置就是所得到的新的一帧的目标位置。判别式跟踪算法是将跟踪过程看作一个分类问题,通过已有的视频序列在线或离线训练分类器,再用训练好的分类器计算下一帧目标位置。文献[6]提出的一种最小平方误差和输出(Minimum Output Sum of Squared Error,MOSSE)跟踪算法,首次将相关滤波应用到目标跟踪领域并取得了很好的效果;文献[7]提出基于核循环结构检测(Circulant Structure of Tracking-by-Detection with Kernels,CSK)跟踪算法,创新地采用了循环结构编码密集采样并用核方法训练正则化最小二乘非线性分类器;之后文献[8]在核相关滤波(Kernelized Correlation Filter,KCF)跟踪算法中使用梯度方向直方图(Histogram of Oriented Gradients,HOG)特征对CSK进行改进。
KCF跟踪算法没有检测目标遮挡的机制,所以无法应对目标严重遮挡的问题;模型更新的学习参数固定,缺乏适应性较强的模型更新策略等。为解决上述问题,提出了结合正样本集的核相关滤波算法。
1 核相关滤波(KCF)跟踪算法
KCF跟踪算法的核心思想[8-9]是利用循环位移进行密集采样得到正、负样本。使用脊回归来训练分类器,并利用循环矩阵在傅里叶空间可对角化的性质将矩阵的运算转化为元素的点乘,大大降低了算法的运算量,提高了实时性。
1.1 循环矩阵
循环矩阵是由目标图像块进行循环位移得到的正、负样本组成的矩阵。其中循环位移操作的变换矩阵为

(1)
通过n次移位可以再次得到原来的信号,是一个循环的过程,因此可以计算出一个循环移位的全集为
{Pux|u=0,1,…,n-1}
(2)
式中:x为感兴趣的图像块,为叙述简便,以单通道、一维图像说明,即x为n×1的向量;u表示循环移位的次数。将循环移位的全集写成矩阵形式即循环矩阵X,为
(3)
循环矩阵有一个很好的性质,即任意循环矩阵经过傅里叶变换后都是对角矩阵。循环矩阵可以表示为
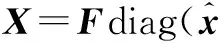
(4)
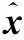
1.2 脊回归模型分类器
相关滤波目标跟踪算法采用脊回归来训练分类器。对所有的训练样本X和期望输出Y通过优化目标函数
(5)
可求得分类器权重为
w=(XHX+λI)-1XHY
(6)
式中:f为分类器函数;xi和yi分别是第i个训练样本和对应的输出;λ为正则化参数防止过拟合。
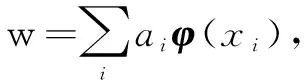
a=(K+λI)-1Y
(7)
式中:I是单位矩阵;K为核矩阵,其形式为Kij=k(xi,xj)=〈φT(xi),φ(xj)〉,〈,〉为点积运算,k为核函数。将式(7)变换到傅里叶频域可得
(8)
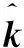
1.3 分类器的快速检测
利用线性分类器检测输入图像z求得其响应,其方程可写为f(z)=wTz。利用核函数进行映射,则方程为
(9)
式中,xi为训练样本。利用循环矩阵性质及核技术,可简化计算得到
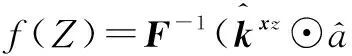
(10)
式中:F-1表示傅里叶逆变换;⊙为点乘运算。然后查找所有测试样本响应f(Z)的最大响应位置作为目标的预测位置ppre_ppos。
1.4 参数更新
(11)
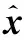
2 结合正样本集的核相关滤波跟踪算法
2.1 正样本集的建立
正样本集就是在跟踪过程中采集到的正样本的一个集合,正样本集定义为
P_s={pos_si|i=1,2,…,n}
(12)
式中:P_s为正样本集;pos_si为正样本集中的正样本。
以每次通过式(10)求得的目标预测位置为中心进行3×3的采样,采样框的大小为初始目标框的大小x×y,将得到9个待测样本,测试样本定义为
T_s={test_sj|j=1,2,…,9}
(13)
式中:T_s为测试样本集;test_sj为测试样本集中的测试样本。
利用归一化互相关(Normalized Cross Correlation,NCC)算法[10-11]对正样本集中的正样本与待测样本集中的待测样本进行相似度计算,来判断待测样本是否为正样本,NCC算式为
(14)
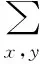
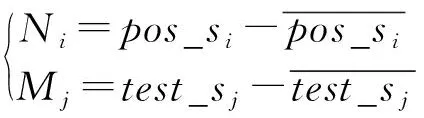
(15)
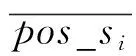
通过式(14)可以得到正样本集与待测样本集的相似度矩阵Sscore,计算相似度矩阵Sscore中的最大值max_Sscore及相应的测试样本ttest_smax,即
max_Sscore=max(Sscore)
(16)
当max_Sscore的值大于0.85时,将相应的测试样本加入正样本集中,即
(17)
如果max_Sscore大于0.75,将测试样本ttest_smax在原图中对应的位置作为目标最终的预测位置Ppos,否则目标最终的预测位置Ppos就为Ppre_Ppos。
2.2 遮挡判断及参数更新
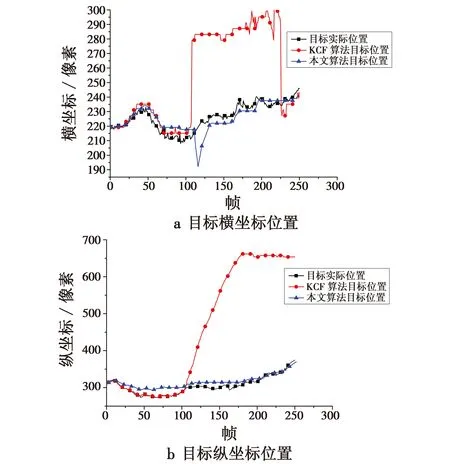
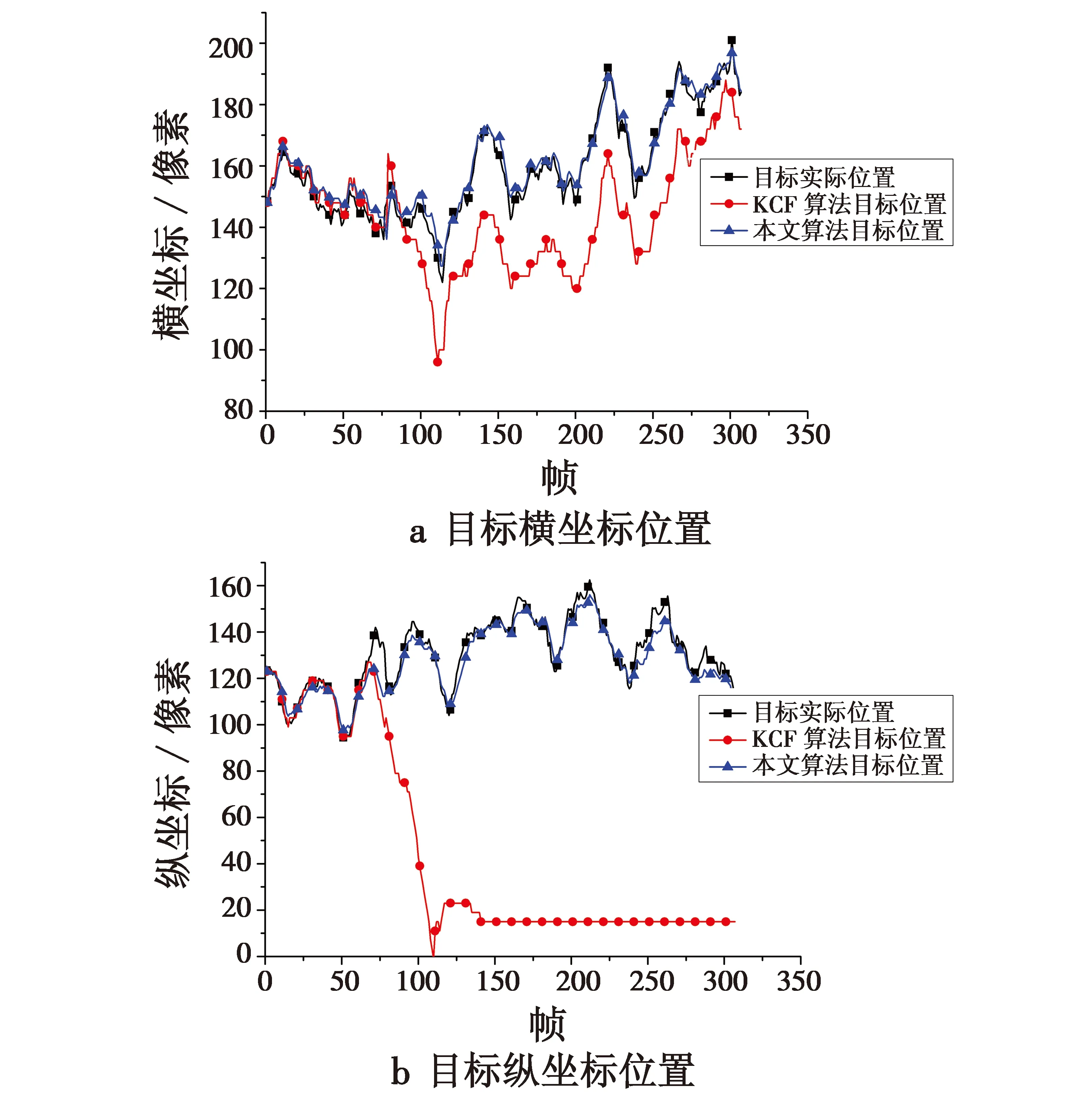
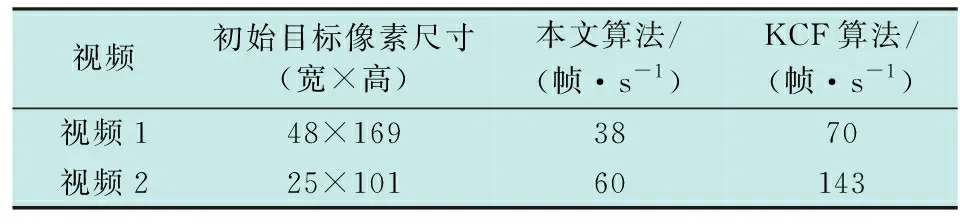
从上文计算可以得到相似度矩阵中的最大值max_Sscore,当max_Sscore>0.85时,目标未遮挡;当0.75 (18) 结合上文的算法改进分析,在KCF跟踪算法的基础上,本文所提出的跟踪算法流程如图1所示。 图1 跟踪算法流程图Fig.1 Flow chart of the tracking algorithm 实验的硬件环境为Intel 酷睿i5 3210M 2.5 GHz CPU,8 GiB RAM;软件环境为Matlab2015a。下面展示了视频1(分辨率像素大小为640×480,共250帧)、视频2(分辨率像素大小为352×288,共307帧)。跟踪结果如图2、图3所示。 图2 视频1跟踪结果Fig.2 Tracking results of Video 1 图3 视频2跟踪结果Fig.3 Tracking results of Video 2 3.2.1 跟踪准确度分析 利用跟踪目标的中心位置的坐标与实际位置中心坐标的差的绝对值,作为跟踪结果准确性的度量方法。实验对视频1和视频2的跟踪位置的横、纵坐标进行了分析,如图4、图5所示。 图4 视频1跟踪位置曲线图Fig.4 Tracking position curve of Video 1 图5 视频2跟踪位置曲线图Fig.5 Tracking position curve of Video 2 图4与图5分别展示了2个视频在KCF算法与本文算法下目标横纵坐标与实际横纵坐标位置曲线。在图4中的第110帧和图5中的第65帧附近,目标被遮挡,KCF算法发生了严重的漂移,跟踪位置远离了目标。而本文算法在目标发生遮挡后,有小幅度的漂移,但目标再次出现时,能够迅速地再次跟踪上目标。对于视频1,KCF算法得出的跟踪结果与目标实际位置平均偏差(29,154)像素,而本文算法的平均偏差为(4.5,11.2)像素;对于视频2,平均偏差分别为(17.5,86.1),(2.8,3.9)像素。 3.2.2 算法实时性分析 两种算法的跟踪速度见表1。 表1 跟踪速度 跟踪速度是由帧数与跟踪时长的比值定义的。可以发现KCF算法的跟踪速度都大于本文算法的跟踪速度,虽然本文算法的跟踪速度有所降低,但是没有影响到视觉的流畅性,仍能满足实时性的要求。 本文提出了建立正样本集,利用正样本集与待测样本集的相似度来建立目标遮挡的判断机制,有效地减少了把遮挡物当作目标的情况,并且采用了多段学习率的更新方式,提高了模型的准确性。本文算法的不足之处是:目标尺度不能自适应以及对目标严重形变的鲁棒性不好,这些都是下一步的研究重点。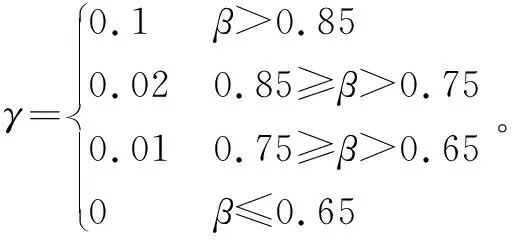
2.3 算法流程
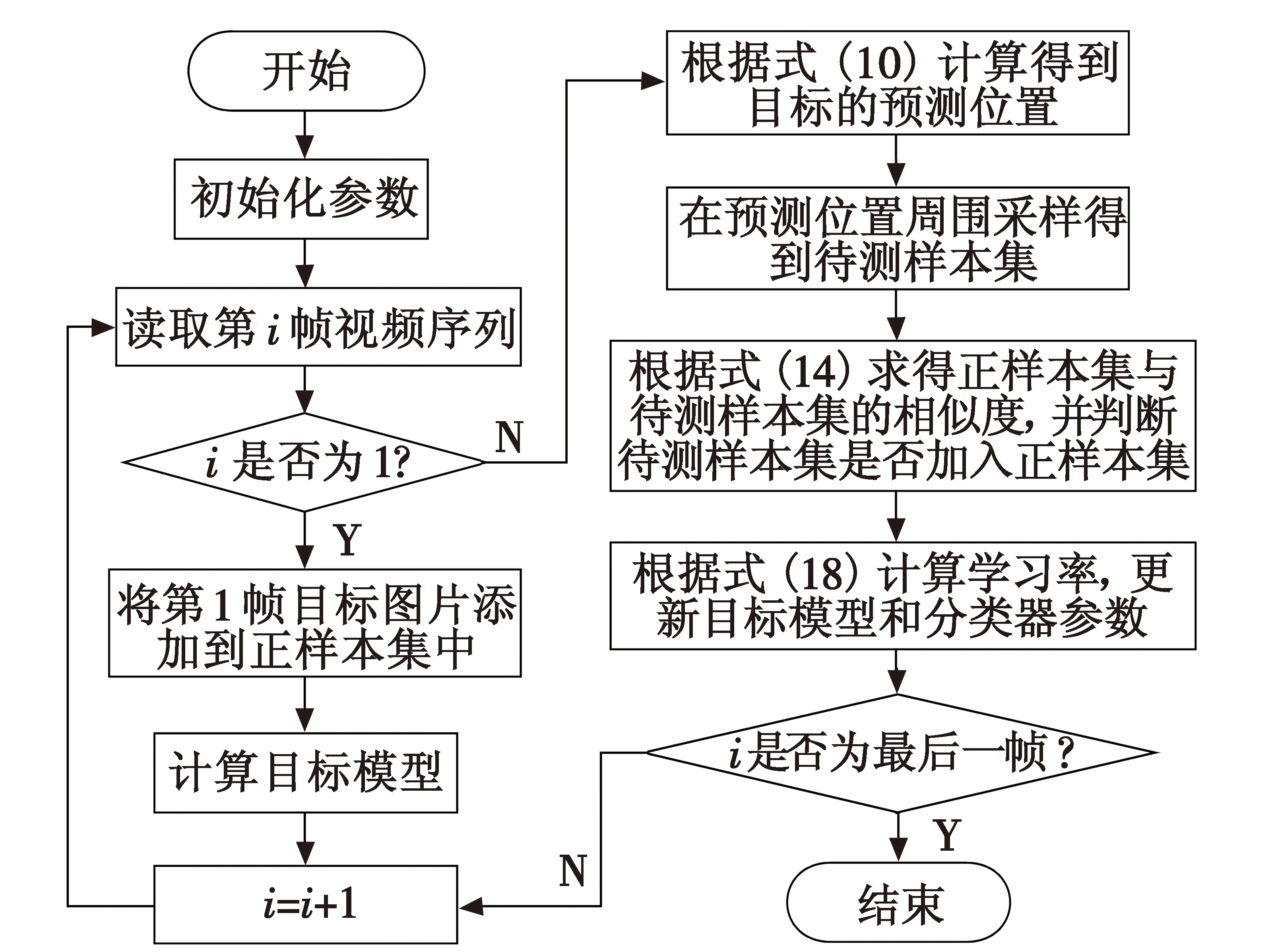
3 实验结果与分析
3.1 跟踪效果展示


3.2 跟踪结果分析
4 结束语
