基于HMM和信息熵的分布式传感器协同任务规划研究

张耀中, 姚康佳，郭 操

(1.西北工业大学电子信息学院，西安 710129; 2.沈阳飞机设计研究所,沈阳 110035)

0 引言

随着无人作战平台以及各类机载传感器载荷技术的快速发展，分布式无人平台传感器在战场中发挥越来越重要的作用。但是，分布式多传感器系统由于作战环境的复杂性、地理位置的分散性以及战场活动的不确定性为任务系统的调度带来了挑战。通常战场环境中的各种真实状态都是隐藏的，其真实状态只能通过各种分布式传感器的观测值推断得来[1]。隐马尔可夫模型(Hidden Markov Model,HMM)作为一种参数化表示的用于描述随机过程统计特性的概率模型，是一个双重随机过程，由两个部分组成：Markov链和一般随机过程[2]。由于战场环境中各种真实状态的演化都是隐藏进行的，可以将其看作是一个隐藏的随机过程序列，完全可以从分布式传感器的观察序列中对相应的真实状态进行概率推断，从而寻求战场环境中所隐藏的真实系统状态。

本文针对多无人平台搭载多传感器进行协同任务探测为研究目标，以HMM思想和信息熵理论为支撑，以战场环境的不确定性和传感器执行任务的损耗模型为出发点，以单位传感器执行给定任务的损耗所带来的信息增益大小为目标函数建立了基于单链HMM和多链HMM过程的动态传感器任务规划模型[3]。同时针对一些特殊情况下的传感器任务调度策略，通过引入风险成本的概念，在保障任务完成的同时能很好地降低使用无人机平台搭载传感器执行任务的风险，为战场环境中不确定性建模和分析奠定了基础。

1 分布式协同传感器规划建模

1.1 变量定义

若一个随机过程演变的将来状态仅依赖于现在时刻，而与过去时刻无关，称该过程为随机Markov过程[4]。在战场态势感知过程中，真实的战场状态通常是隐藏的，只能通过各种类型传感器的观测值进行推断，对应的Markov过程就是一个双重随机过程，即HMM过程：一个是隐含的状态转移序列，它对应一个单纯的Markov过程，另一个是与隐含状态相对应的观测序列[5]。在战场环境中需要探测的每个任务都可以看作是一个HMM过程。

假设任务探测时刻为k∈{1,2,…,K}，系统中有N个离散的HMM过程，u(k)⊂{1,2,…,m}为k时刻可用传感器集合，m为系统中传感器的数量，设定一个传感器观测序列对应一个HMM过程。定义k时刻系统的状态转移概率矩阵为A(k)，观察概率矩阵为B(k)，若初始状态的概率分布为φ,则HMM模型定义为[6]

Λ(k)=(A(k),B(k),φ)k=1,2,…,K

(1)

k时刻N个HMM过程的状态转移概率集合可以表示为A(k)={A1(k),…，Ar(k),…，AN(k)}，其中，Ar(k)表示第r个HMM过程的状态转移概率矩阵

Ar(k)=[arij(k)]={P(xr(k)=srj|xr(k-1)=sri)}

(2)

式中,xr(k)表示HMMr在k时刻的隐状态[7]，xr(k)∈{sri:i=1,2,…,nr}，nr为HMMr的隐状态数。

同理，k时刻N个HMM过程中的观察概率矩阵为

B(k)={B1(k),…，Br(k),…，BN(k)}。

(3)

设定yr(k)为k时刻通过传感器探测获取到的观测值，yr(k)∈{Or1(k),…，OrL(q)(k)}，由于不同类型传感器的功能特性不同，因此观察值个数取决于所分配传感器的种类。若k时刻没有传感器分配给HMMr过程，那么观察值的集合为Φ。定义brliq(k)为k时刻系统状态xr(k)=sri时，分配给HMMr的传感器观测到Orl(k)(l=1,2，…，L(q))出现的概率，则

Brq(k)=[brliq(k)]=
[P(yr(k)=Orl(k)|xr(k)=sri,μr(k)=q)]

(4)

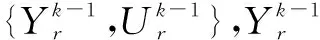
(5)

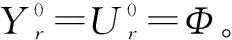
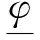
(6)

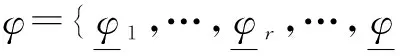
若系统中只有一个探测任务，则对应只有一个HMM过程，此时N=1，相对应的状态转移概率矩阵和观察概率矩阵以及初始状态分布概率也只有一个，可视为多链HMM过程的一种特殊情况。

1.2 多传感器规划的成本模型

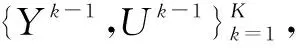
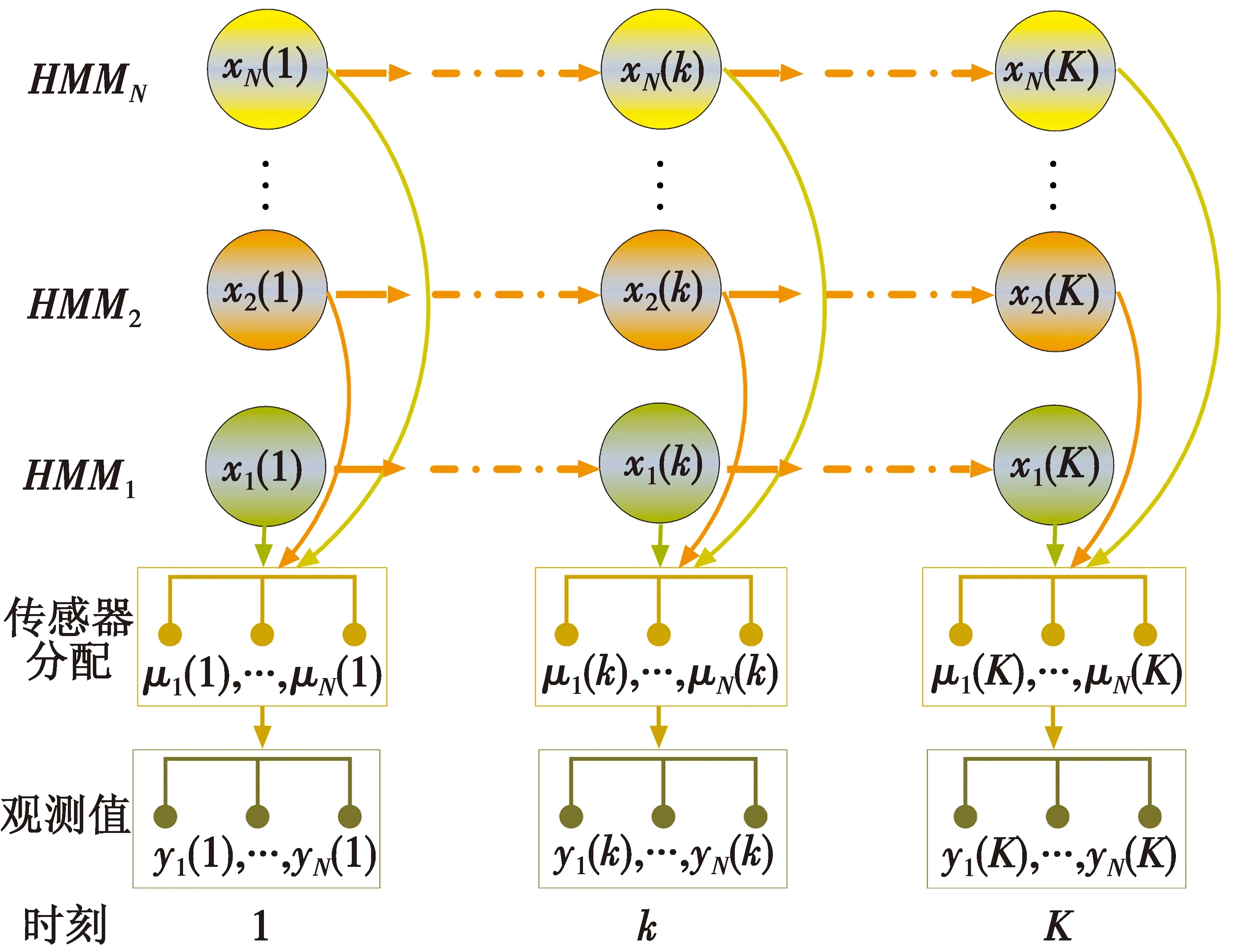
图1 基于HMM的传感器规划问题图示Fig.1 HMM-based sensor planning

为了便于问题的分析，引入系统信息状态的概念以描述N个HMM过程中的随机性，定义如下

(7)

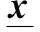
(8)

在k时刻，HMMr中传感器的使用总成本可以表示为

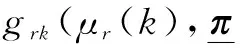
(9)

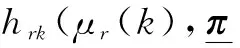
传感器使用成本定义为

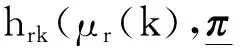
(10)

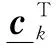
(11)

式中：(ar,br)和(aμr(k),bμr(k))分别表示HMMr所关联的任务和传感器μr(k)的位置坐标；v(μr(k))为传感器μr(k)(或所搭载平台)的移动速度。

1.3 多传感器规划的目标函数

为了解决战场环境中分布式多平台传感器分配问题的不确定性和随机性因素，将信息熵引入传感器动态规划模型中，以信息增益和传感器执行任务过程中的成本损耗为切入点，定义多传感器动态分配过程的目标函数。

假设在k时刻，所有可选的传感器分配方案集合为ξ(k)，规划模型需要在ξ(k)中选择最优的分配方案δ*(k)，以最大化每个传感器损耗单位成本所获取的信息增益，即最大化不确定性的减少量。本文中采用随机变量πr(k|k-1)的信息熵H(πr(k|k-1))来指示其平均不确定性，也表示它所携带的平均信息量[2]。当πr(k|k-1)的某个可能值概率为1时，H(πr(k|k-1))=0，即随机变量的取值是确定的；当所有的可能值出现的概率相同时，随机变量πr(k|k-1)的平均不确定性最大。结合信息状态概率式(7)得到信息状态πr(k|k-1)的熵表达式为

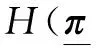
(12)

同理，μr(k)=q的信息熵为

H(μr(k)=q)=

(13)

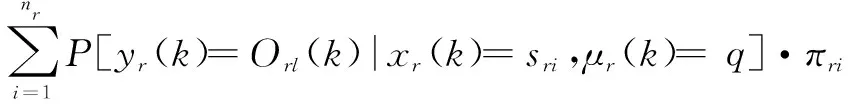
(14)

设随机变量X和Y，条件熵H(X|Y)表示已知Y时，X所具有的平均不确定性，表达式为

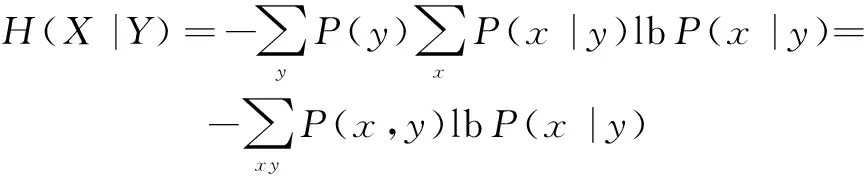
(15)

式中，P(x,y)为随机变量X和Y的联合概率，P(x,y)=P(y)P(x|y)，则H(X|Y)可以进一步表示为

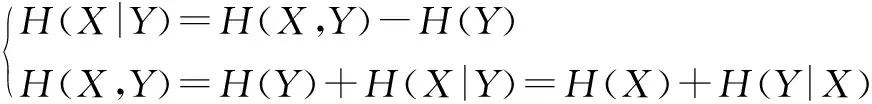
(16)

式中，H(X,Y)为联合熵，可以理解为熵的分解，即X和Y的联合不确定性可以分解为X(Y)的不确定性加已知X(Y)时Y(X)的不确定性[8-9]。结合条件熵的定义式(15)和全概率公式，H(X|Y)可表示为当Y取所有可能值时的全概率形式。

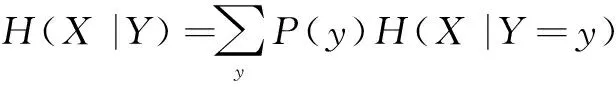
(17)

因此，由上式可得

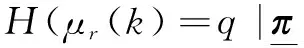
(18)

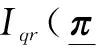
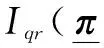
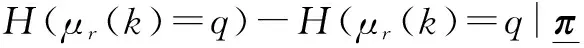
(19)

将式(13)、式(14)和式(18)代入式(19)，可以得到最终的信息增益表达式为

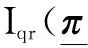
(20)

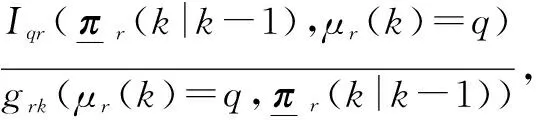
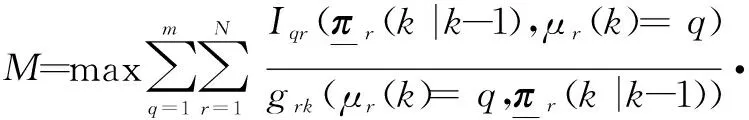
(21)

1.4 多传感器的最佳任务探测序列

由于战场中的真实状态是隐藏的，其真值只能通过各种传感器的观测值推断而来，战场环境无法实时准确确定，因此选取合适的传感器探测任务序列，能保证对战场环境的全面感知。

已知δrq(k,i)，获取δrq(k+1,i)的递推公式为

(22)

利用记忆变量Ψrq(k,i)记录概率最大路径上当前状态的前一个状态。并且根据当前状态以及对下一状态的预测，通过目标函数——单位成本下的信息增益，选择合适的传感器执行目标任务，并且根据执行任务的结果作为下一时间阶段的决策依据。不断进行这一过程，可以得到在不同时刻下用于执行任务的传感器序列，即多传感器的最佳探测任务序列。

1.5 分布式多传感器协同任务规划过程

分布式多传感器动态任务规划过程如图2所示。

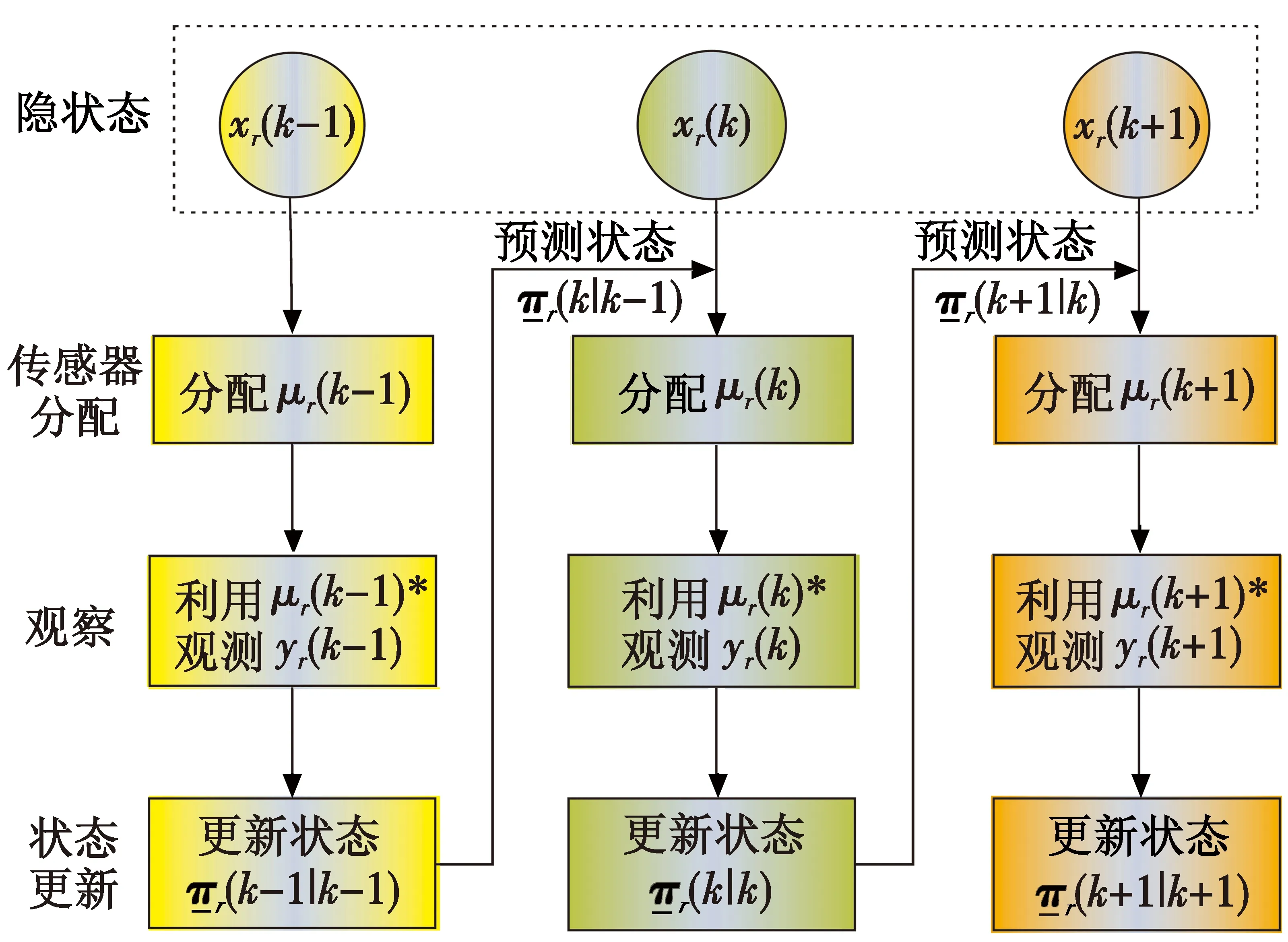
图2 基于HMM的多传感器动态规划过程Fig.2 Multi-sensor dynamic programming based on HMM

首先，设定初始的模型参数，所选择的参数可以通过经验值设定，也可以通过Baum-Welch算法进行模型参数的重估。针对k时刻的HMMr过程，算法的执行步骤如下所述。

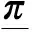
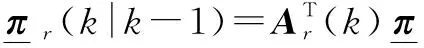
(23)

2) 生成信息增益矩阵。分配给每个HMM过程的传感器获取的信息增益值不同，因此，利用式(20)分别计算每个传感器-HMM过程的单位传感器使用损耗带来的信息增益量，得到m×N的信息增益矩阵为

(24)

3) 传感器分配。通过式(21)得到满足约束条件并且使目标函数值最大的传感器任务分配矩阵δ*(k)。

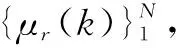
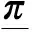
(25)

6) 算法迭代。如果k=K，算法结束，输出最佳的状态转换序列，从而得到战场态势预测结果；否则更新k的值为k+1，转至1)。

2 特殊情况下的多传感器调度问题

在使用无人机平台搭载传感器执行任务时，由于平台和传感器均存在发生意外的概率，导致无法顺利完成规划的任务，敌方可能对执行任务的无人机平台进行打击。这些突发情况给任务的执行带来极大的不确定性，从而使传感器任务调度更加复杂。

2.1 无人机平台损失时的多传感器调度

在无人机平台执行任务的过程中可能会发生意外，导致无人机平台损失。无人机作为传感器的搭载平台，一旦损失，对应所搭载的传感器同样丢失，无法再次使用。

给定无人机由敌方击毁和非敌方击毁(技术原因坠毁或气象环境原因坠毁)造成的无人机丢失的概率，设定a表示敌方击毁无人机的概率，b表示非敌方击毁造成无人机丢失的概率，可知a+b=1。把无人机丢失之前是否传回目标地点的信息分为两种情况：一种是无人机传回目标区域的探测信息；另一种是无人机未传回目标区域的探测信息。两种情况对应不同的状态概率分布，使用Sstate表示系统的综合状态更新。

无人机传回目标区域的探测信息为

Sstate=b*D+a*P

(26)

式中：D表示无人机的探测数据，即无人机探测所得的目标状态；P表示指挥官给出的无人机被击毁情况下，待探测区域状态的概率分布；a表示敌方击毁无人机的概率；b表示非敌方击毁造成的无人机丢失的概率。

无人机未传回目标区域的探测信息为

Sstate=b*G+a*P

(27)

式中，G表示系统的估计状态概率分布值。式(26)、式(27)均用来计算状态更新值。

具体处理过程如图3所示。

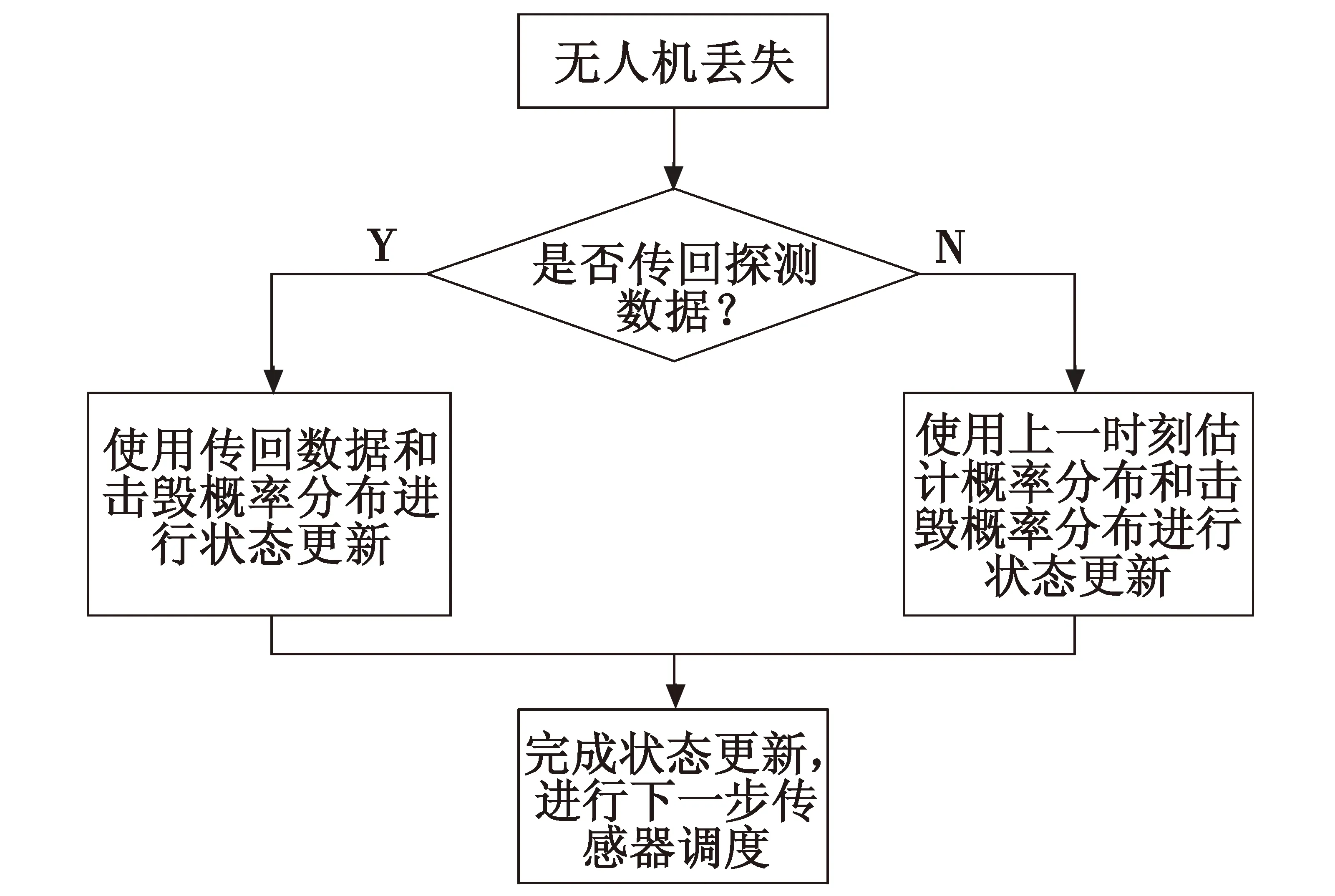
图3 平台损失情况下的传感器动态规划过程Fig.3 Dynamic planning process of sensorsunder loss of UAV platform

2.2 考虑风险成本的多传感器调度

由于战场环境不同，无人机执行任务所面临的风险大小也不相同。为了减少不必要的无人机资源损失，在实际使用过程中有必要将无人机平台执行任务时的风险成本引入到任务规划中来。

将风险成本与多传感器使用成本和移动成本相结合，从而影响多平台传感器的任务规划过程。将传感器的使用成本与移动成本称为常规成本，使用ucost表示；风险成本用rcost表示。得到传感器使用总成本Tcost的表达式为

Tcost=ucost+kr*rcost

(28)

式中，参数kr可用于调节风险成本在任务决策中产生的影响，表示在进行决策时决策者愿意承担的风险大小，kr越大表明承担的风险越小，即在进行任务分配时风险成本占决策的比重较大；反之表明可接受的风险越大。

设定风险矩阵R=[Rij]为无人机平台在不同状态下的使用风险，在本文中定义风险值为多架该类无人机平台在该战场状态下执行任务被击毁的无人机在所有无人机中所占的比例。Rij是指在状态为Si、无人机平台为无人机j时的风险值。风险矩阵可以是指挥官的经验值所得，也可以是通过真实和模拟实验得到的风险值。定义综合风险为当前状态概率分布下传感器平台的总风险值，用zfj(k)表示为

(29)

式中，φ(k)表示当前时刻(k表示时刻)的状态概率分布。

3 仿真案例

设定指挥官要实现对5个远海无人岛礁的监控，以防止敌方占据岛礁对周围海域构成威胁，有多架无人机平台可以调度，每架无人机平台可以携带不同的传感器载荷，假定同一时刻每个待监控的岛礁只能派出一架无人机平台去执行任务。采用HMM算法模型启动传感器动态任务规划过程，设定平台传感器的使用损耗、位置和速度以及各个HMM过程所关联的任务等初始属性信息，为了便于算法求解，假定系统中的所有HMM过程均采用统一的状态划分，并且观察值的数目相同。对不同目标岛礁的状态划分如表1所示。

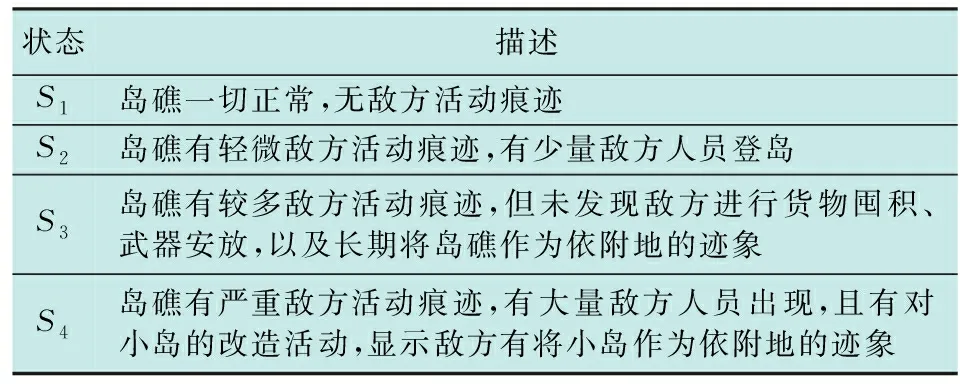
表1 岛礁观测状态

指挥官决定每周对5个岛礁进行一次任务探测，并且依据历史数据获取得到岛礁不同状态之间的转移概率。具体参数如下所示。

不同任务对应的状态转移概率矩阵为：

相应HMM过程的初始状态概率分布如表2所示。

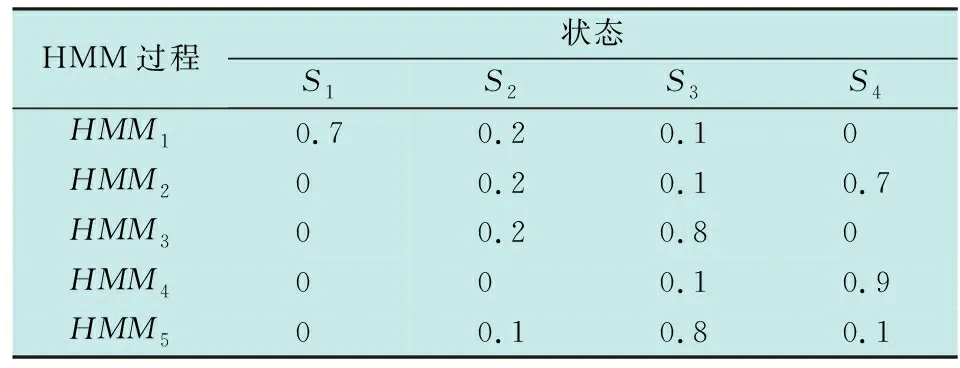
表2 不同HMM过程的初始状态转移概率

3.1 多平台传感器调度仿真

由以上仿真场景设定，可以计算出在不同时刻最佳的传感器任务调度序列，其中6个周期的任务调度序列如表3所示。

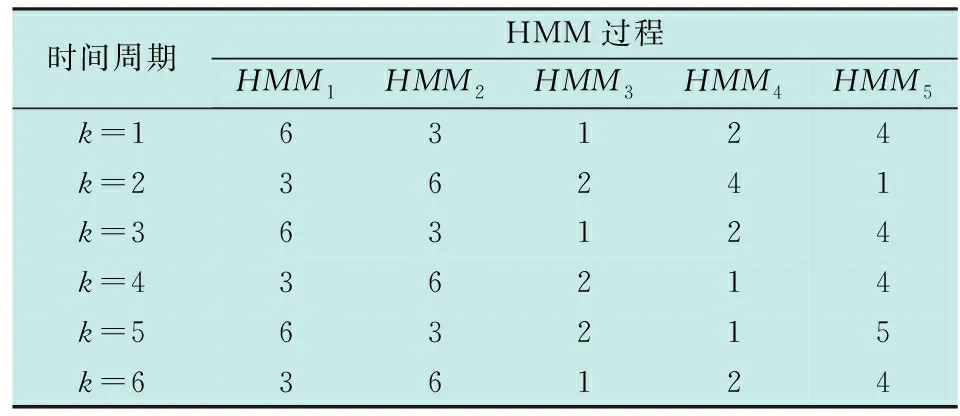
表3 不同岛礁不同时刻的平台传感器规划结果

表3中针对每个平台传感器的不同性能和探测任务需求，给出了6个时间周期(k=1,2，…,6,k表示时间周期)的平台传感器调度使用方案，每个岛礁对应一个HMM过程，表3中的数字表示对应时刻对每个HMM过程所调度无人机平台的序号。

3.2 考虑风险成本的多平台传感器调度仿真

在考虑无人机执行任务时的风险情况下，设定当前有9个无人机平台可供调度,分别标号为无人机1,2,…,9，对上述设定的任务场景执行探测任务，给定9个无人机平台传感器的探测概率矩阵B为

给定系统中的平台使用风险矩阵R为

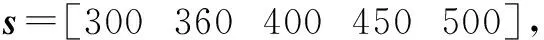
设定风险成本调节参数kr=0.4，仿真得到时刻1到时刻6(k=1，2，…,6,k表示时间周期)的无人机任务调度序列(用无人机的编号标示)。为了便于分析对比，将每个时刻前往所有目标地点执行任务的无人机平台的综合风险值之和称为本次调度的任务风险，使用F(k)表示，算式为

(30)

仿真中针对是否考虑无人机平台执行任务时的风险成本进行了对比分析，仿真结果如表4～表6所示。

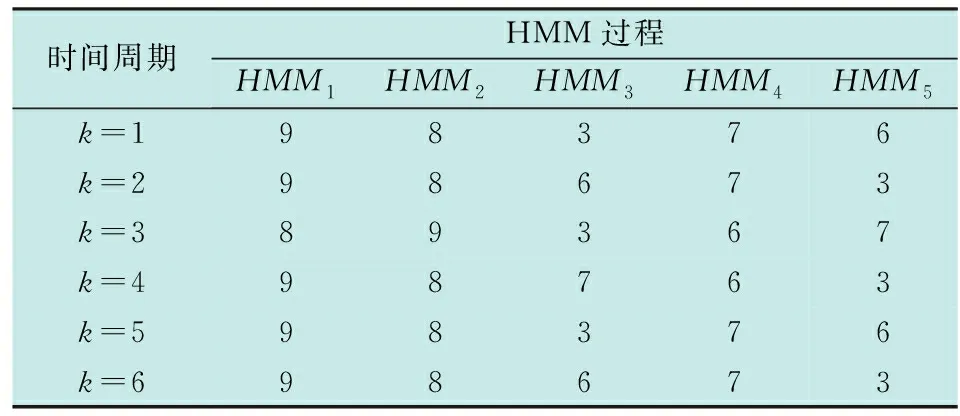
表4 不考虑风险成本时的平台传感器规划结果

表5 考虑风险成本时的平台传感器规划结果

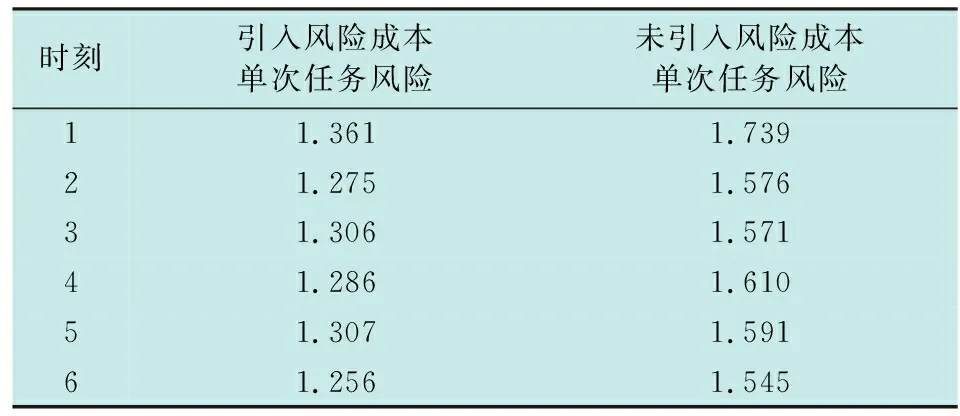
表6 不同时刻两种决策方法的风险比较

仿真结果表明，引入无人机平台的使用风险成本对任务执行成本进行扩展,在很好地进行传感器调度的同时能减小无人机平台的使用风险，有利于提高无人机执行任务时的生存力。

4 总结

本文以多平台传感器最优任务规划为目标，结合隐马尔可夫建模理论，建立了基于信息熵理论的传感器调度决策模型，从而使针对特定任务的多平台传感器调度使用的成本最优化。在此基础上，研究了在一些特殊情况下的传感器动态调度策略，为减少无人机平台的使用风险，提出了包含风险成本在内的扩展任务成本的概念，并基于此进行了无人机平台传感器的任务调度仿真。仿真结果表明，通过对传感器平台的优化调度，可以在平台使用风险最低的情况下达到多传感器平台的调度成本最优化目标，从而为战场环境中不确定性建模和分析奠定了基础。