基于FPGA的工业机器人运动控制器设计
2018-12-17刘宏乐
刘宏乐,李 兵
(1.华北理工大学,河北 唐山 063210;2.唐山学院,河北 唐山 063000)
0 引言
随着电子技术与信息技术的不断发展,机器人正在逐渐地进入到工业领域中,尤其是在高端制造业和工业自动化生产中发挥着重要作用。运动控制系统是工业机器人的核心,它向驱动装置发出任务信号,控制末端的执行装置实现对被控对象的位置、速度等参数的精准控制。为此,就需要设计一个行之有效的运动控制器对给定轨迹进行实施跟踪。
根据控制器控制核心的不同,运动控制器主要有三大类型:PC型、嵌入式型、全软件型,并向多轴化、网络化、开放式、智能化、可重构性等方向发展[1]。
依据运动控制器的上述类型及特点,为了达到良好的控制效果,专家们已经进行了很多的尝试,在运动定位策略方面,根据不同的工况环境,有针对性地提出了决策树、模糊逻辑、遗传算法、人工神经网络等智能算法与传统PID相结合的方法[2]。传统的PID控制因为结构简单易懂,在大部分的工业自动化系统中都有它的存在,但是在碰到复杂的系统时,由于无法获得准确的数学模型,难以整定PID的参数,因而无法获得预期的效果。本文的研究对象为六自由度工业机器人,目前还无法建立准确的模型。考虑运算的实时性、控制的准确性、硬件设计的复杂性及可重构性,本设计选择模糊PID作为运动控制器的核心算法。在运算的实时性方面,模糊算法实际上是一种离散的算法,无论选择软件执行还是硬件执行,在执行速度方面优于其他算法。因为模糊算法是一种经验性算法,一般情况下决策树、遗传算法、人工神经网络算法在运动控制的准确性方面要优于模糊算法,但如果模糊控制规则选择得当,该算法也能够满足控制需求。在硬件设计的法则性方面,无论是采用PLC、单片机、DSP、嵌入式还是可编程逻辑芯片,模糊算法的实现都是最为容易的。在可重构性方面,如果采用的是纯软件设计方法(PC机)、PLC、单片机、DSP或嵌入式等方法,要根据重构需求重新修改软件程序,同时还要更换相应的数据采集或通信接口等设备,成本比较高,周期也比较长[3]。如果采用的是FPGA,根据重构需求,通过修改程序即可设计出相应的电路系统,数据采集、通信接口电路的更改也可以通过修改程序来实现,可大大降低重构成本和周期。因此依托于FPGA设计模糊PID运动控制器更为简单、易懂,开发周期更短,设计成本也更低。
1 伺服系统的传递函数
本设计中选择的六自由度工业机器人为ABB的IRB-2600ID,在伺服电机的驱动下,相邻的关节之间的动态性能可由下面的方程表示[4]:
(1)
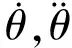
(2)
该微分方程即为六自由度工业机器人的传递函数。
2 模糊PID算法
由于六自由度工业机器人的伺服控制系统为非线性控制系统,传统的PID控制在位置控制效果方面不能满足要求,因此要将PID与模糊逻辑相结合对系统进行控制。模糊PID控制是根据PID控制器的3个参数与偏差e和偏差的变化ec之间的模糊关系,在运行时不断检测e及ec,通过事先确定的关系,利用模糊推理的方法,在线修改PID控制器的3个参数,让PID参数可自整定[5]。在线实时调整控制器的kp,ki,kd这3个参数,得到整理后的Δkp,Δki,Δkd作为输出。因为Δkp,Δki,Δkd这3个数一直是动态变化的,所以它们会根据系统的实时变化来整定自己的参数。PID控制参数的计算用到下列公式:
kp=kp0+Δkp
ki=ki0+Δki
kd=kd0+Δkd,
其中kp0,ki0,kd0为初始数据。
3 运动控制器的硬件实现
目前工业机器人的主流控制器有DSP、嵌入式、工控机、PLC等,这些控制器的结构与外设相对固定,使得控制缺乏灵活性,运算速率相对较低,实时性较差。虽然FPGA发展较晚,但它具有强大的计算能力及优异的可重构性,在控制器的开发设计以及升级改造等方面有着其他控制器无法匹及的优势[6]。图1为基于FPGA的模糊PID控制器电路结构。
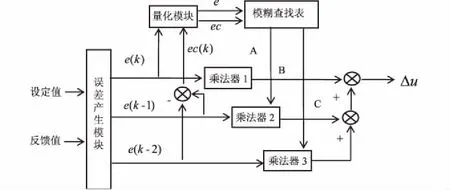
图1 基于FPGA的模糊PID控制器电路结构
系统分为4个模块:误差产生模块、量化模块、模糊查找表模块以及运算模块。误差产生模块生成e和ec的精确值;量化模块就是把精确的e,ec变成模糊值;模糊值进一步经过模糊查找表,输出PID参数,最后通过一定运算,输出最终的Δu值。本设计采用的FPGA型号为Altera公司的EP4CE40F29C8N。
3.1 误差及误差变化量模块设计
本模块的设计中输入是误差e以及误差变化率ec,利用连续的两个误差e得到误差变化率ec。整体设计采用的是原理图设计方法,利用FPGA中固有的运算模块来进行浮点运算,精确度更高,与传统的编程语句实现方法相比较,该方法在消耗的硬件资源方面不占有优势,但是在运算精度上却要高出传统方法。由于所选择的FPGA具有丰富的逻辑单元,在电路结构上的消耗可以忽略。在时钟CLK作用下同时将给定值与输出反馈值送入两个LPM_ADD_SUB模块,同时接入两个锁存器,这样送入第二个LPM_ADD_SUB模块的值相对于第一个来说要差一个周期,那么两个LPM_ADD_SUB模块分别产生第k次和k-1次误差。最后将这两个误差送入第三个LPM_ADD_SUB模块中,输出误差变化量。在离散化论域中,误差变化率的值通常是用误差变化量的值来替代的。设计该模块主要实现的是一个减法功能,于是调用了QuqrtusⅡ模块库中的LPM_ADD_SUB。图2为误差模块设计原理图。
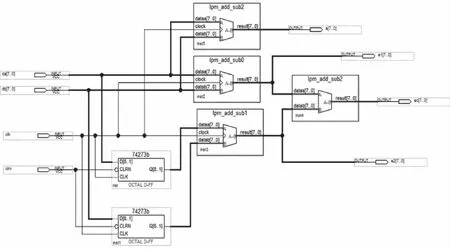
图2 误差模块设计原理图
3.2 模糊量化模块设计
上一个模块中输出的e与ec是精确的量,但是模糊控制器的输入是模糊值。为了得到模糊值就需要将精确值经过量化。设计此模块,首先是将e与ec的模糊论域与实际论域根据实际情况设定出来;其次将模糊论域依据各个成分,把实际论域分成几个段,每一段对应于一个模糊论域中的一个成分。划分论域时,如果划分过细,会造成规则数目太多而使得电路结构过于复杂,运算速度降低;如果划分过粗的话,则无法达到精确的控制。IRB-2600ID型六自由度机械手臂的执行机构为伺服电机,由于伺服电机本身的控制为闭环控制,精度较高,因此在模糊论域的划分上,权衡了控制精度与系统的复杂程度后,采用的是七级编码机制,模糊语言变量划分为7个以下论域集合{NB,NM,NS,ZO,PS,PM,PB},即{负大,负中,负小,零,正小,正中,正大},因此本文中将误差大小量化为7个等级。当从现场采集到数值后,将机器人关节的旋转角度误差e与误差变化率ec作为输入。根据ABB IRB-2600ID工业机器人产品手册可知,轴1的工作范围是-180°~180°,因此将e与ec的实际论域范围定为[-180,180],量化因子为60,采取四舍五入的方式,把实际论域分成7段,分别是[-180,-150],[-150,-90],[-90,-30],[-30,30],[30,90],[90,150],[150,180],对应到模糊论域范围[-3,3]上,即{-3,-2,-1,0,1,2,3}。假设误差的精确值是57,此精确值在[30,90]的论域段,误差经过量化后的值就是1,量化地址为100。ec和e的量化过程相同,表1为e/ec的量化地址。

表1 模糊量化后的e/ec的量化地址
这部分采用VHDL语言进行设计,其部分代码如下显示:
PROCESS(E,EC,CLK)
BEGIN
IF CLK'EVENT AND CLK='1'THEN
IF E<=-180 THEN A<="111";
ELSIF E>=-180 AND E<=-150 THEN A<="000";
ELSIF E>=-150 AND E<=-90 THEN A<="001";
ELSIF E>=-90 AND E<=-30 THEN A<="010";
ELSIF E>=-30 AND E<=30 THEN A<="011";
ELSIF E>=30 AND E<=90 THEN A<="100";
ELSIF E>=90 AND E<=150 THEN A<="101";
ELSIF E>=150 AND E<=180 THEN A<="110";
ELSIF E>=180 THEN A<="111";
END IF;
…
END IF;
END IF;
END PROCESS;
C<=A&B;
Q<=C;
END ART;
该模块如图3所示。
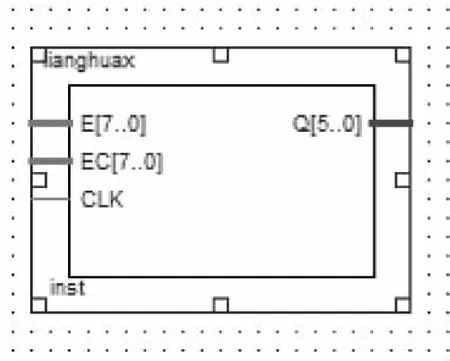
图3 量化模块
3.3 模糊查找表模块设计
模糊控制器中,模糊查找表是至关重要的。由于在现实中模糊化运算、模糊推理和清晰化计算是非常繁复的,在线的演算量较少,故本文主要运用离线运算方式,这种方式不仅改善了FPGA的工作效率,而且编程的困难也有所消减。
为了得到Δkp,Δki,Δkd的值,主要通过Matlab建立模糊PID模型,在Matlab中得到相应的值。为了减少难度,可设A=Δkp+Δki+Δkd,B=-(Δkp+2Δkd),C=Δkd。
通过计算得到以e和ec为输入,以A,B,C为输出的表格。高3位是e的量化地址,低3位是ec的量化地址。表2-表4即为A,B,C的模糊控制表。

表2 A模糊控制表
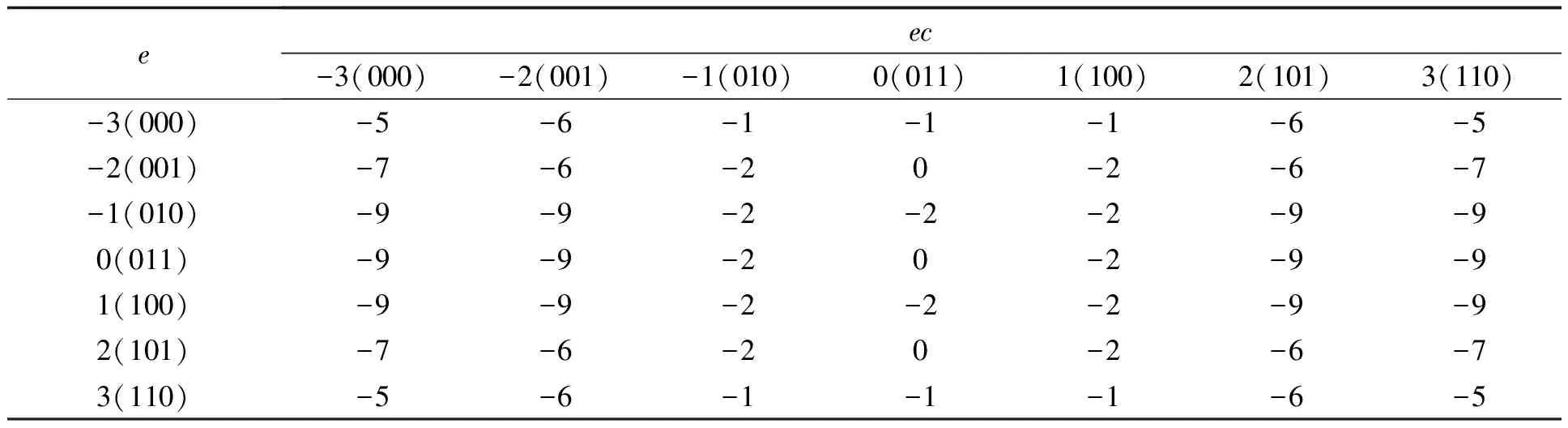
表3 B模糊控制表
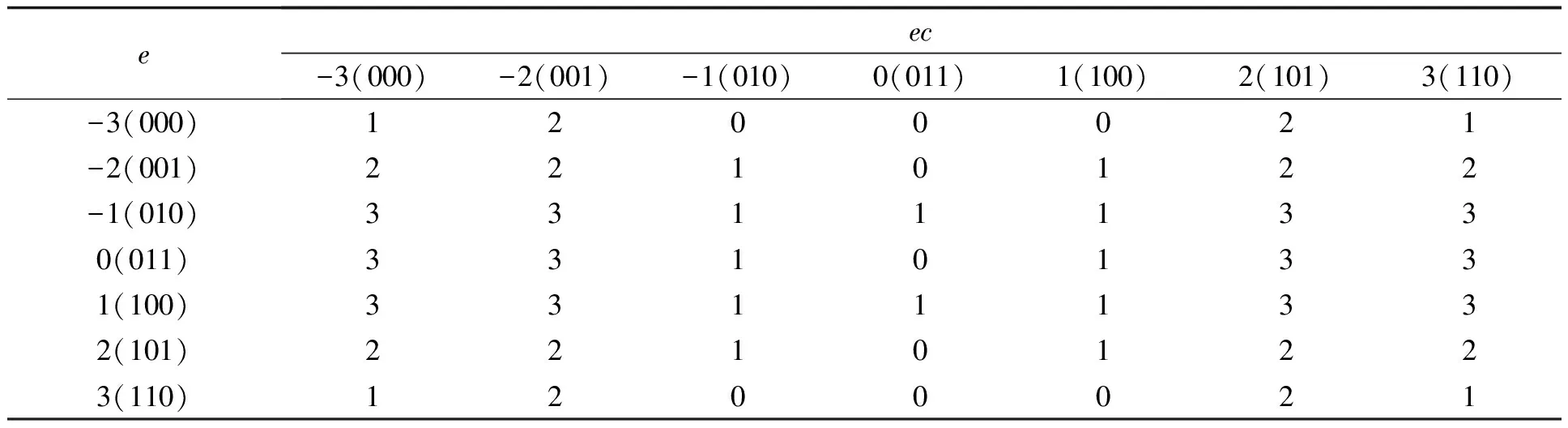
表4 C模糊控制表
为了更好地运用A,B,C模糊控制表,需要将它们制作成ROM模块,而ROM模块的核心就是MIF文件。将这些设计完后,此时只需要计算:
Δu(k)=Ae(k)+Be(k-1)+Ce(k-2)。
(3)
图4为A的MIF文件。
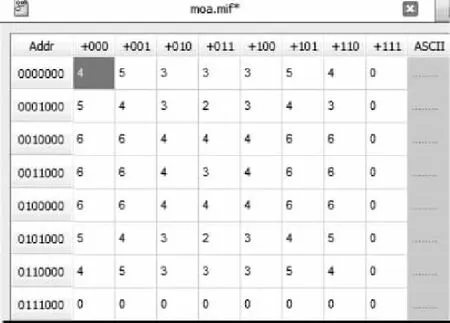
图4 A的MIF文件
3.4 运算模块设计
乘法运算模块调用了函数库里的LPM_MUITA。让e(k),B与e(k-1),C与e(k-2)相乘,进一步使用parallel_add,使这3个参数通过加法功能获得最后的结果Δu。图5为运算模块原理图。
3.5 顶层模块设计
图6就是模糊PID算法的顶层模块。首先输入通过误差模块获得的精确值,量化模块把e和ec进行量化,得到模糊值;其次将量化后的值送入到下一个单元以查表的方式进行离线查询,得出控制参数的增量;最后将计算得到的3个参数A,B,C输入到下一个模块,通过计算得到输出。
取一组数据,如da=11,db=9,则可以得到e=2,e1=2,e2=5,ec=-3,e精确值是2,属于[-180,180]这个论域,其量化值是0,量化编码是011。同理可得ec的量化编码是011。把e的量化编码设为高3位,ec的量化编码设为低3位,查表可知A=3,B=0,C=0,通过公式(3)计算得到Δu=6。电路仿真结果如图7所示。
4 结语
由电路仿真结果可以看出,电路运算结果与理论计算得出的结果是一致的,说明设计中所采用的方法能够满足控制需求。电路运行的延迟时间为11 ns,确保了执行的实时性。控制器整体占用FPGA资源的58.5%,确保了后续升级重构需求。
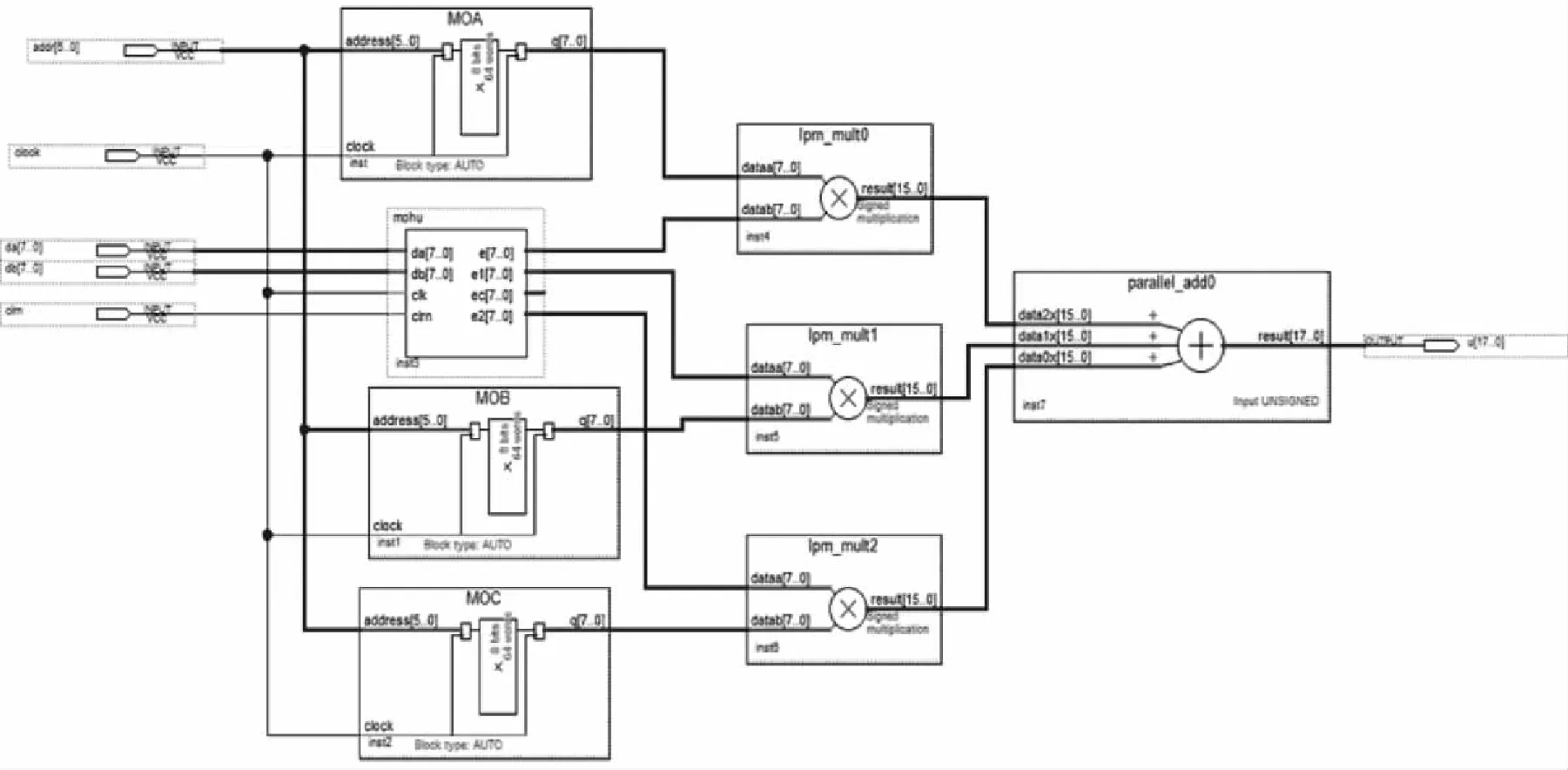
图5 乘加运算模块原理图
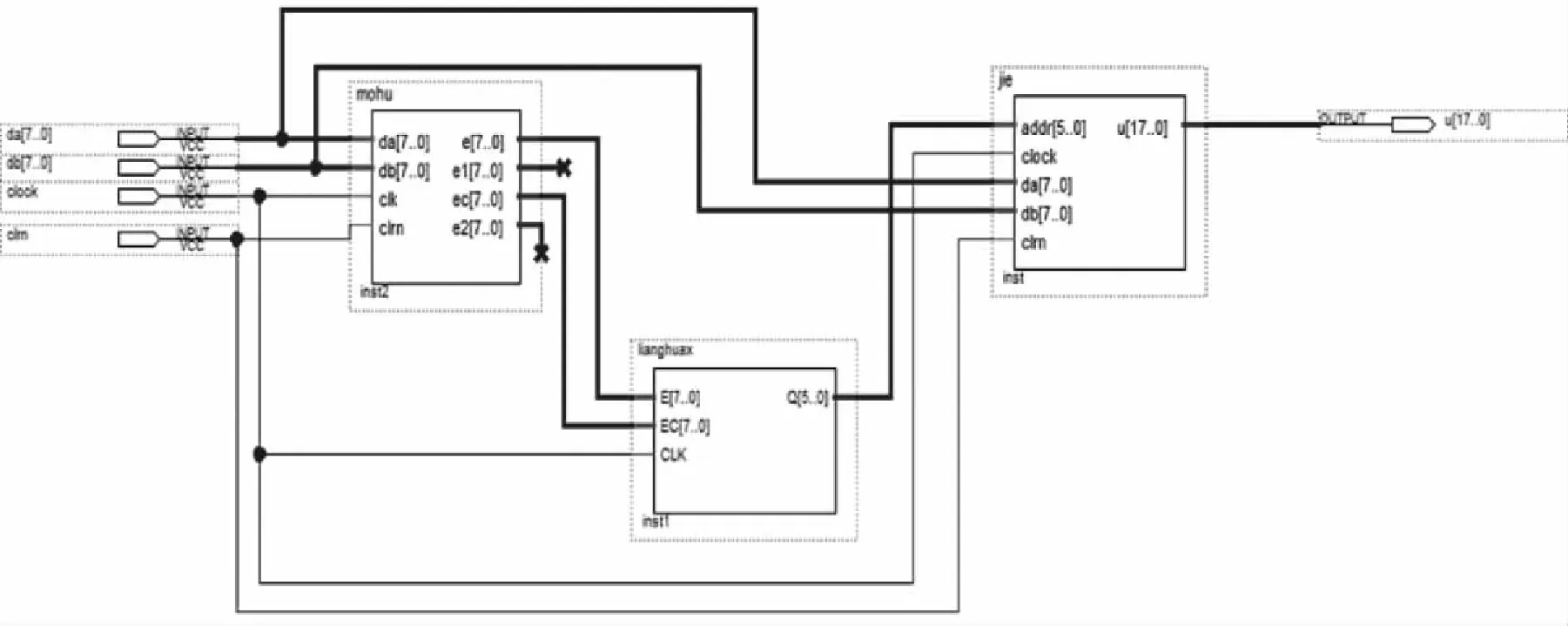
图6 模糊PID算法顶层模块
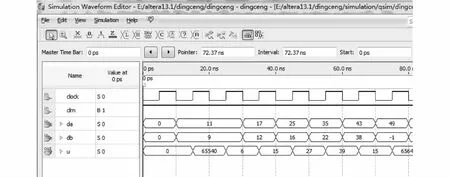
图7 电路仿真结果
