基于Kalman滤波算法的运动目标跟踪系统建模与仿真

甘志英

(唐山学院 智能与信息工程学院，河北 唐山 063000)

0 引言

运动目标跟踪是机器视觉领域研究的热点与难点。对运动目标进行跟踪不仅可以提供目标的运动状态和轨迹，也为运动分析、场景理解等提供可靠的数据来源，因此运动目标跟踪系统在智能监控、突发事件检测等方面有着重要的应用。运动目标跟踪系统一般包括两部分，一是运动目标检测，二是运动目标跟踪[1]。传统的运动目标检测算法有三种：光流法、背景差分法、帧间差分法[2-4]，其中背景差分法是目前运动目标检测技术中应用最广泛的一种方法。常用的运动目标跟踪算法主要有基于目标轮廓的跟踪和基于目标特征的跟踪，前者利用目标的边界信息来实现跟踪，可有效克服干扰及遮挡问题，但易受跟踪的初始化影响[5]；而后者利用目标的特征进行匹配，在目标部分遮挡时，利用部分特征仍能进行跟踪，常用的特征有目标质心、颜色特征、角点等[6]。

针对传统跟踪算法鲁棒性和实时性不足的问题，本文基于kalman滤波算法构建一种运动目标跟踪系统，此系统使用背景差分法检测运动目标，通过Kalman滤波预测目标下一状态的位置，并根据当前检测结果，更新Kalman滤波状态。

1 背景差分法

背景差分法是利用视频序列中不含前景目标的帧图像作为背景，将各帧图像的像素值与背景的像素值相减，得到差值图像，再进行二值化运算即得到目标。由于该方法实现简单、速度较快，且便于硬件实现，因此被广泛应用。

1.1 背景的获取

最简单的背景获取方法是统计平均法，即将视频序列帧的灰度平均值作为背景图像。在视频序列中背景相对于目标出现的次数多很多，视频序列平均值和背景值接近。背景Bn(x，y)的获取用式(1)表示：

(1)

1.2 运动目标提取

用视频序列各帧Dn(x，y)与背景图像作差分。取差值超过阈值Th的像素为目标，低于Th的为背景，得到目标二值图像Gn(x，y)：

(2)

该方法计算简单，易于实现，经简单处理就能快速检测出运动目标位置，但不适用于摄像机运动或者背景变化的情况。

2 Kalman滤波算法

Kalman滤波算法是一种求线性最小方差误差估计的算法，在时域内设计滤波器，采用状态方程描述随机变量的变化，并且算法是递推的，适用于平稳和非平稳过程。其基本思想是：建立随机变量随时间变化的状态方程，在对随机变量进行实时观测下，利用Kalman滤波方程组获取其在全局条件下的最优估计。Kalman滤波算法用如下两个模型描述随机变量[7]：

X(k+1)=AX(k)+BW(k)，

(3)

Y(k)=HX(k)+V(k)，

(4)

称式(3)为状态方程，式(4)为观测方程。其中，X(k)为随机变量k时刻的n×1维状态；Y(k)为对应状态的m×1维观测信号；A为状态转移矩阵；B为噪声驱动矩阵；H为m×n维观测矩阵；W(k)为输入白噪声，方差为Q；V(k)为观测噪声，方差为R。

根据上述模型，Kalman滤波方程组包含预测部分和更新部分，具体流程如下：

状态预测：

我汪文斌，1974年生于浙江杭州。中国美术学院硕士研究生毕业。现为杭州画院创作展览部副主任、杭州油画院秘书长、国家二级美术师、中国美术家协会会员、浙江省美术家协会理事、浙江省油画家协会理事。

(5)

协方差预测：

P(k+1|k)=AP(k|k)AT+BQBT。

(6)

滤波增益矩阵：

K(k+1)=P(k+1|k)HT[HP(k+1|k)HT+R]-1。

(7)

状态更新：

(8)

(9)

协方差更新：

P(k+1|k+1)=[In-K(k+1)H]P(k+1|k)。

(10)

3 仿真结果及分析

在Matlab环境下进行仿真实验，分析运动目标的观测位置和估计位置的差异。实验对象为一段小球运动的视频图像序列。首先获取一帧只有背景的图像(由多个视频帧图像取均值获得)，用背景差分法检测到运动目标，提取运动目标的中心及大小，并用绿色星型点构成的圆圈进行标记。

设计状态方程及观测方程，并设置初始状态。

其中状态方程为：

(11)

其中，(x，y)：小球位置；(vx，vy)：小球速度；dt：采样时间间隔；g：重力加速度。

观测方程取：

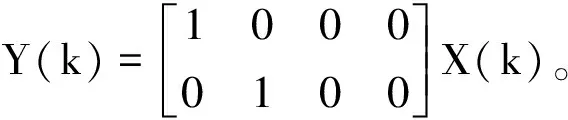
(12)

初始状态取：

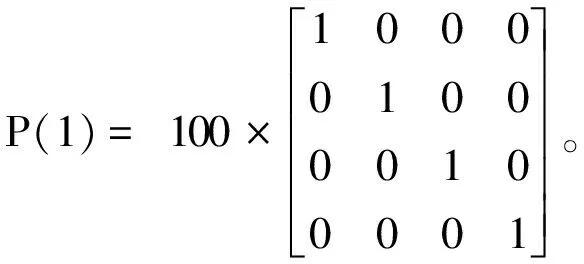
(13)

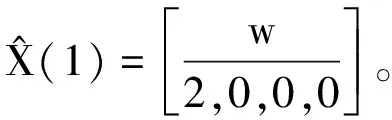
其中，w为图像宽度。

观测位置：y(1)取第一帧背景差分检测位置。

用Kalman滤波算法进行预测跟踪，跟踪结果用红色点型圆圈标记，如图1所示。

(a)第1帧 (b)第3帧

(c)第5帧 (d)第7帧

(e)第9帧 (f)第11帧

(g)第13帧 (h)第15帧

(i)第17帧 (j)第19帧

(k)第21帧 (l)第23帧

(m)第25帧 (n)第27帧

(o)第29帧 (p)第31帧

(q)第33帧 (r)第35帧图1 运动目标跟踪结果

图1中图像(a)到(e)为小球下落过程，其中在使用背景差分法检测时，(c)(d)中小球含有虚影，被认为目标变大；在(e)中小球开始着地，竖直速度发生突变。(f)到(n)为小球反弹上升过程，之后的图像为小球下落与上升的重复，直至停止。

图2描述了运动目标在跟踪过程中竖直方向上观测位置与Kalman滤波估计位置的差值，绿色星点线表示观测位置，红色圆点线表示估计位置。从图2中可发现，小球在下落过程中(1到10帧)，跟踪效果较好；在反弹上升过程中(11到28帧)，由于小球速度突变，观测位置与估计位置的差值较大，后随着Kalman滤波的调整，差值逐渐减小。

图2 竖直方向观测位置与估计位置的差值

实验说明在小球稳定的运动中，Kalman滤波跟踪效果很好；但在小球运动状态发生突变后，该方法需要一定时间的调整才能改善跟踪效果。

4 结论

本文对基于Kalman滤波算法的运动目标跟踪系统进行了建模分析，使用背景差分法检测目标观测位置，采用Kalman滤波预测目标位置，通过设计状态方程及观测方程，设置合理的初始状态，在Matlab环境下进行仿真实验，仿真结果证实了该算法的有效性，能满足实时有效地对运动目标进行定位跟踪，算法精度较高，具有一定的鲁棒性和准确性。