卧式矩形截面螺旋通道内气液两相流压力降特性研究
2018-12-14吴家禹周云龙
孙 博,吴家禹,周云龙
(1.东北电力大学 电力运行仿真中心,吉林 吉林 132012;2.国电电力发展股份有限公司大连开发区热电厂,辽宁 大连 116600;3.东北电力大学 流体机械安全节能技术工程实验室,吉林 吉林 132012)
螺旋管具有空间利用率大、可自由膨胀及重心低等优点,并且比直管有更佳的传热特性[1],是一种具有良好应用前景的高效换热管型.从理想角度考虑,换热管段设计应该是在不增加压降的基础上提高换热性能.因此,准确的估计换热管段的压降是设计换热管段的关键.近来,不同形状及尺寸螺旋通道内的流动机理越来越受到重视.但是,有关矩形截面螺旋通道内两相流的流型和压降的研究报道还是很有限的.
目前,对于圆形截面螺旋通道内气(汽)水两相流动特性已有广泛的研究[2~5],但对于其他截面形状的螺旋通道,大部分还停留在数值研究阶段[6],实验研究比较少.而仅有的对于矩形截面螺旋通道的实验研究也多是针对单相流体所进行的流场结构及流动特性的研究.张丽等[7]对低雷诺数下高宽比为3.5的矩形螺旋通道流场进行了实验测量,测量值与数值模拟值吻合较好.C.J.BOlinder,B.Sunden[8~9]对正方形截面螺旋通道内层流流场进行了测量.对于管内两相流的压降,Zhao&Bi[10]指出如果管内的单相摩擦阻力能够被接受,那么两相流的摩擦阻力压力降就能够用L&M关系式来预测.但是对于矩形截面螺旋通道内两相流流动这样复杂的现象,需要进一步改善两相流摩擦阻力压力降的计算方法.
本研究以空气-水为工质,实验测定了压差信号,对卧式矩形截面螺旋通道内空气-水两相流动压力降特性进行研究,并找出与矩形截面螺旋通道吻合较好的数学模型,对前人有关方法进行了修正,最后给出了各流动工况下摩擦阻力的计算公式.这对促进工程实际相关方面的发展具有重要的意义.
1 实验系统与装置
试验是在水/空气试验台上进行的.试验系统及试验段实拍图,如图1(a)、图1(b)所示.

图1 试验台流程图及试验段实拍图
通道由一个外壁带螺旋翅片的圆柱和一个外套管围成,为了实现可视化研究,材质采用有机玻璃,螺旋翅片由车刀车出,与外套管的配合公差小于1 mm.外套管内径120 mm、厚5 mm,翅片高22 mm,螺旋翅片厚度6 mm,螺距110 mm.所围成的矩形截面的长、宽分别为24 mm和22 mm.通道当量直径为23 mm,曲率为0.47,挠率为0.36.本实验中,有效直管段的长度为550 mm,即5倍螺距.
水和空气分别在离心式水泵和空气压缩机的动力推动下流经电磁流量计和热式气体质量流量计,经两相混合器充分混合后流入实验段,而后经旋风分离器分离,水流回水箱继续循环使用,空气排入大气中.空气压缩机额定工作压力为0.8 MPa,实验过程在常温下进行,压力参数范围为0.1 MPa~0.3 MPa.空气的折算速度范围为0.2 m/s~15 m/s,水的折算速度范围为0.2 m/s~1.2 m/s.本实验使用差压变送器采集机压差信号通过数据采集器输入计算机,并通过专门软件处理.为保证测量信号的实时性,设定采样频率为512 Hz,采集时间为10 s,准确记录了压降与流量的信号变化.同时计算机还连接高速摄影仪,记录较为典型的流型.本次实验选择顶端相距2倍螺距的两个取压点采集压差信号,两点在同一水平线上.实验采用的差压变送器在实验前使用电子手操器进行了量程校准.整个实验台的测量信息,如表1所示.

表1 测量参数和设备误差
实验系统安装完毕正式实验前,首先对整个实验系统进行水洗,清除系统中的沉积物对实验系统的影响,然后对压力压差传感器进行仔细的标定、校核、检查.对于水空气两相流实验,首先固定水的流量,改变气体流量使之从小到大间断变化,直至气体流量达到最大.在每一间断点工况下,观察并待流型稳定后进行记录和数据采集.完成一个循环后,然后在增大水的流量,重复调节气的流量.实验完毕后,应先关闭供水回路,再关闭供气回路.
2 实验结果及分析
2.1 单向流实验结果分析
在进行气-液两相流实验前,为了验证测量系统和实验系统的精确性和合理性,先进行单相水在卧式矩形截面螺旋通道中的阻力特性实验.本单向流试验中,经测得计算出的单相水的最小雷诺数为16 087,远大于临界雷诺数,故本实验中单向流体的流态全部为紊流.计算螺旋管内单向流体在紊流区的摩擦阻力系数常用的关联式有White(1929)[11]、Ito(1959)[12]、Srinivasan(1968)[13]等,由于本实验管路形状不同,用实验数据计算所得结果与上述关联式所得结果均有出入,但与应用Ito关联式计算的结果较为相似.故以Ito的方法为基础,通过拟合的方法对关联式系数进行修正,得到了较符合实验数据的关联式为
(1)
在实验数据范围内,拟合公式与实验数据所计算出的结果误差在3%左右(见图2),能够较准确的预测本实验管段单向流体的摩擦阻力系数.
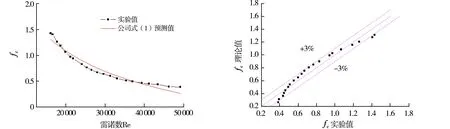
(a) fc与Re的关系 (b) fc实验值与预测值波动图图2 单相摩擦阻力实验值与预测值的比较
2.2 空气-水两相流实验结果分析
相比较单向水的实验研究来看,两相流在矩形截面螺旋通道内的流动更为复杂,影响通道内摩擦阻力的因素也有很多,对于研究气-液两相流在矩形螺旋通道中的流动也更具有实际的工程意义.对于气液两相流的摩擦阻力已经有了一些研究,但还没能有一个公认可通用的计算摩擦阻力的关联式,对于矩形螺旋通道内摩擦阻力的关联式则更少见.
2.2.1 影响摩擦阻力的因素
两相流的压降包括摩擦压降、重力压降及加速压降,即
ΔPTP=ΔPf+ΔPa+ΔPg,
(2)
在本试验中,由于流体是水平流动,所以不考虑重力压降的影响;在空气-水两相流中没有热量的传递,质量流率也不发生变化,因此加速压降也不做考虑.故上式可化简为
ΔPTP=ΔPf.

(3)
影响两相流摩擦阻力压力降的因素有很多,主要有管子的粗糙度、几何尺寸、两相流流动方向、热流密度、质量流量及干度等.针对本实验管段而言,可忽略粗糙度、结构、流向等方面的影响,然而矩形螺旋通道内气-液两相流摩擦阻力受干度和质量流量的影响比较大.由实验数据计算所得出的摩擦阻力压力降随干度和质量流量的变化曲线,分别如图3、如图4所示.从图3中可以看出,当质量流量一定时,矩形截面螺旋通道内的摩擦阻力随着干度的增加而增大,二者间基本呈现线性关系.从图4中可以看出,当干度一定时,矩形截面螺旋通道内的摩擦阻力随着质量流量的增加也随之增大,而且变化趋势是越来越快.
2.2.2 计算两相流摩擦阻力的关联式
本节将试验结果分别于均相流模型和分相流模型的预测结果进行对比,并分析得出哪一种模型最适合预测矩形截面螺旋通道内两相流的摩擦阻力压力降.
(1)均相流模型
均相流模型是假定气体与液体均匀混合,被看做为一种单相流体,其流动的物性参数取两相介质相应参数的平均值.这种方法是一种最简单的分析模型方法,同时也是单相流体力学的直接延伸.气-液两相流体的摩擦阻力压力降计算式可写成和单相流体时相似的形式:
(4)
将ρm=1/(x/ρG+(1-x)/ρL)带入式(4)整理后得到
(5)
式中:φ为摩擦阻力压力降的校正系数,φ值与干度x、压力p以及假定汽-水混合物全部为水时在通道中的流速u0有关.米洛保尔斯基、陈立勋[14]等进行过实验,得到了修正系数φ的曲线图或计算式.

图5 均相模型摩擦阻力系数实验值与理论计算值对比
本实验计算结果,如图5所示,给出了两相流在矩形螺旋通道内摩擦阻力系数的实验值与均相流模型预测值得对比.从图5中可以看出,实验值与预测值得偏差极大,且关于摩擦阻力系数λm随着雷诺数Rem的变化趋势也与均相流模型的理论预测不相符.这是因为均相流模型是假设气相和液相之间是无滑移的,而对于矩形截面螺旋通道内的气-液两相流动,弹状流、分层流、雾状流特别明显,如图6所示.很难使两相介质能够均匀混合,所以这种情况是不切实际的.因此,均相流模型方法不适用于处理本文实验数据.

图6 两相流在矩形截面螺旋管内的流型
(2)分相流模型
分相流模型是把气-液两相流动看成是气相和液相各自分开的流动且两相之间互相作用,是一种考虑了实际流动体系中两相具有不同物性和速度的工程模型计算方法.Lockhart-Martinelli[15]分相模型是最早提出并被广泛应用至今的摩擦压降计算方法,其公式为
(6)
(7)
(8)


图与χ的关系

(9)
式中:a、b、c为参数;f(θ)为修正系数;θ为物性参数、流动参数和几何参数的函数.

(10)


图8 实验值与预测关联式的比较图9 两相摩擦因子φ2L的实验值与预测值的比较
应用新的计算关联式的拟合曲线和实验所测得数据的对比,如图8所示.可以看出应用新的方法计算矩形截面螺旋通道内气-液两相流的摩擦阻力压降更为准确,如图8所示.应用新的计算关联式计算两相流体在螺旋管内摩擦阻力压力降与实验值的对比,如图9所示.预测值和实验值的平均偏差在20%以内,可以说明新的计算关联式计算摩擦阻力压力降与实验值吻合较好,相比较Lockhart-Martinelli分相模型,新的计算关联式更准确.
3 结 论
(1)通过对单向流实验结果的分析研究,修正得到了新的关联式,能够很好的预测单向流体在卧式矩形截面螺旋通道内的摩擦阻力压力降.
(2)通过对气-液两相流实验结果的分析研究,可以发现干度和质量流量是影响两相流摩擦阻力压力降的主要因素,随着二者的不断增大,两相流的摩擦阻力压力降变化较大.

