基于CAR模型的用电量需求预测研究
2018-12-14周小琳
周小琳
(东北电力大学 经济管理学院,吉林 吉林 132012)
用电量需求预测是规划电力发展、指导电力建设的重要依据.准确地预测全社会用电量需求是有效避免电力短缺和电力浪费、保障国家或地区社会经济系统平稳运行的关键.国内学者使用多种方法进行用电量需求预测,这些方法各有利弊,但总体上来说,用电量需求预测的方法体系并不完善.时间序列方法,如线性回归模型、指数平滑预测模型和趋势移动平均法、自回归模型[1]等,其优点是参数少、模型简单易操作,但是模型的预测精度较低、无法体现天气等因素引起的非线性变化;支持向量机算法[2~3]能够最小化结构风险,小样本情况下泛化能力较强、适用于非线性和高维度问题的短期预测;灰色关联法[4~5]的优点是模型算法简单、参数少、容易实现,但该方法对模型参数具有较大的敏感性、模型预测精度不高;随机森林算法[6]和分位数法[7~8]不仅能够给予预测对象的确定性预测,还能够在出现天气变化等极端事件时保持较高的预测精度,但其缺点是算法复杂、输入变量多、难以实现;神经网络法[9~10]学习能力强、在极端天气情况下仍然保持较高的预测精度,但模型算法结构复杂、运算量大、容易发生过拟合,导致泛化能力不足.
假设某一地区用电量的时间序列为{Yt},如果服从ARMA(n,n)模型,用算子形式可以写成φ(B)Yt=θ(B)θt.在实际应用中,序列{Yt}除了受自身和白噪声(εt)滞后的影响外,有时还要受到控制变量{Xt}的滞后影响,从而使模型变成:φ(B)Yt=ρ(B)Xt+θ(B)εt.则此模型称为受控的自回归滑动平均模型,简记为CARMA(n)模型.CARMA(n)模型不仅能够反映事物发展的自身运用规律,还能够体现复杂系统的动态特征,具有结构风险最小、适用于小样本、非线性、有效克服过拟合、泛化推广能力强、预测精度高的优点,但由于辨识CARMA(n)模型比较复杂,实践中通常假设θ(B)=1,即用一个充分高阶的多变量自回归模型(CAR模型)来逼近并替代CARMA(n)模型,而CAR(n)模型计算简单、且可以自动辨识.国内文献关于CAR(n)模型的研究较少,本文试图把CAR(n)模型应用到用电量需求预测领域,以期找到更加精准的用电量需求预测方法.
1 多变量时间序列CAR模型度量方法
1.1 CAR模型的参数估计
CAR(n)模型参数估计的方法主要包括最小二乘法、递推最小二乘法、广义最小二乘法和递推增广最小二乘法等.在总干扰的均值为零且相互独立的条件下,采用最小二乘法或者递推最小二乘法进行参数估计.当系统的总干扰是相关序列时,最小二乘估计和递推最小二乘估计是非一致估计量,广义最小二乘法、递推增广最小二乘法通过引进一个白色滤波器,把具有相关性的总干扰转化为白噪声,从而使得参数估计保持一致性.P维输入向量、1维输出向量的CAR模型可以表述为
(1)
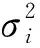
令:B=[φ1,…,φn,ρ10,ρ11,…,ρ1n,…,ρp0,ρp1,…,ρpn]T=[β1,…,βn+(n+1)n]T
置t=n+1,n+2,…,N,并记
YN=(Yn+1,Yn+2,…,YN)T,
EN=(εn+1,εn+2,…,εN)T,
则公式(1)可以写成:
YN=WNB+EN,
(2)
因此,可用最小二乘法求得N时刻参数B的最小二乘估计为
(3)
若有新增观测数据(YN+1,XN+1),则从t=1,2,…,N,到时刻N+1时参数B的递推最小二乘估计为
(4)
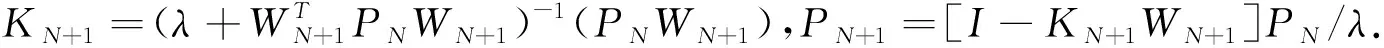
1.2 CAR模型阶数的确定
CAR模型可以用F检验的方法来确定阶数.在给定的观测数据(Xt,Yt),t=1,2,…,N下,可相继地建立模型CAR(n),n=1,2,…,并比较CAR(n)和CAR(n+1),F统计量为
在给定的显著性水平α下,当F≥Fα时,拒绝CAR(n),否则接受CAR(n)模型,从而可确定阶数n.
1.3 CAR模型时滞的确定
2 基于CAR模型的中国用电需求量预测
2.1 数据来源与变量选取
用电需求量与一国的经济规模、产业结构和城镇化率密切相关.本文选取平均每天电力消费量(亿千瓦时)代表用电量需求,用elec表示;以国内生产总值(亿元)代表经济规模,用GDP表示;以国内生产总值中第二产业产值所占比重和第三产业产值所占比重代表产业结构,分别用sindrt和tindrt表示;城镇化率为城镇人口数占总人口数的比重,用urbanrt表示.本文全部数据均来源于国研网数据库.
2.2 用电需求量模型的建立
为克服异方差性,本文中所有变量均采用对数形式,选用lnelec作为输出变量,lnGDP、lnsindrt、lntindrt和lnurbanrt作为输入变量,构建如式(1)所示的1维输出向量、4维输入向量的CAR模型.建模所用F检验的显著性水平为0.05,递推最小二乘法的遗忘因子为1.0,检验结果为F=2.81.定阶检验中CAR(n)模型和CAR(n+1模型的残差平方和分别为0.00016和0.00021,定阶检验的F值为0.07.选定阶次全参数时和剔除不显著因素后模型的残差平方和分别为0.00021和0.00023,是否为不显著因子检验的F值为0.45,F(a=0.05)=4.46.剔除不显著项后的CAR模型为
lnelect= 0.67lnelect-1+0.13lnGDPt+0.25lnsindrts-0.38lnsindrtt-1
0.71lntindrtt+0.51lnurbanrtt+0.32lnurbanrtt-1,
(5)
表1 列出了2001年~2016年我国平均每天电力消费量对数值的实际值和根据式(5)计算的拟合值,2001年~2016年,所有年份电力消费量拟合值与观测值之间的相对误差均不超过1%,平均误差仅为0.35%,可以看出,式(5)的整体拟合效果很好,误差偏离程度非常小,可以用该模型预测我国平均每天电力消费情况.

表1 2001年~2016年中国日均电力消费量对数值的实际值与拟合值
数据来源:作者整理。
3 结 论
本文通过推导1维输出向量、p维输入向量的CAR模型,建立日均用电量需求的预测模型,并采用2001年~2016年我国国内生产总值、第二产业产值比重、第三产业产值比重和城镇化率的数据对模型进行检验.结果显示,本文构建的预测模型中,所有年份电力需求拟合值与观测值之间的相对误差均不超过1%,模型预测精度高、拟合效果好,可以用该模型对中国日均用电需求进行预测.
