基于正态云模型的果蝇优化算法
2018-12-14杜文军
杜文军,孙 斌
(东北电力大学 教务处,吉林 吉林132012)
针对科学研究中的优化问题和工程应用中的复杂问题,研究人员受自然界中生物种群群体行为的启发提出了仿生智能算法,如遗传算法[1]、细菌觅食算法[2]、人工鱼群算法[3]、蚁群优化算法[4]、灰狼优化算法[5]等,这些算法不断发展并广泛应用于流水线调度、电力规划、光谱图像、数字水印等领域,成为人们解决工程科学领域的强有力工具.2012年,学者Pan[6]受果蝇觅食过程中群体行为协作机制的启发,提出一种新的智能优化仿生算法:果蝇优化算法(Fruit Fly Optimization Algorithm,FOA).FOA的实现通过模拟果蝇群体的社会行为获得问题的最优解,算法的寻优规则简单、参数少、寻优能力好,自提出以来受到众多学者的重视和研究应用.对FOA进行改进提高算法的效率是FOA研究主要焦点和方向,目前,对FOA的改进路径包括对算法的内部搜索机制的改进和与其他算法结合的外部改进两个方面.对算法的内部改进主要对算法的搜索步长、最优解的候选机制、果蝇个体的飞行策略等方面进行改进,通过在果蝇个体的位置更新公式中引入权重系数、自适应参数、惯性因子等提高算法的全局搜索能力和局部搜索能力;通过对算法中味道浓度参数的调整、引入逃逸参数、将候选解的产生机制由非线性改为线性等提高算法的寻优精度[7~9];通过对算法中果蝇个体的飞行方向和飞行距离加入随机策略和控制策略提高算法中种群的多样性,避免算法早熟现象[10~12].对算法的外部改进主要通过调整算法的种群规模和种类、与其他算法相结合设计混合式算法等方式,改变算法的种群规模和种类,在算法的寻优过程中对不同的子种群采用不同策略提高算法的全局寻优能力[13~14];引入其他智能算法如差分进化、混沌理论、禁忌搜索等,改进算法的搜索机制以平衡算法的全局寻优能力和局部寻优能力[15~17].
本文在对影响FOA性能的相关参数做分析和研究的基础上,通过对相关文献的研究对FOA进行改进和优化,从理论角度分析了FOA的缺陷,针对现有文献对FOA的改进研究忽略了算法搜索过程中味道浓度参数的随机性、模糊性与不稳定性,将云模型理论引入FOA的改进,利用云模型理论中的正态云描述算法中味道浓度参数的随机性、模糊性与不稳定性属性,改进算法最优解的产生机制,使其自适应动态调整,在算法的嗅觉搜索阶段引入嗅觉灵敏度因子,由嗅觉灵敏度因子自适应动态调整算法的搜索步长,提高算法的全局搜索能力和局部寻优能力.最后,将改进后的算法应用于自动组卷系统,通过与相关研究文献的数据对比,对改进后的FOA算法做了性能分析.
1 FOA原理概述及算法表述
1.1 FOA算法原理
自然界中的果蝇在觅食过程中呈现出显著的社会群体行为,在觅食过程中,果蝇个体对腐烂食物的味道及其敏感,在飞行过程根据嗅觉器官感受到的食物发出味道的浓度,向群体中的其他个体发送信息,同时接受群体中的其它个体发送的信息,从而使整个群体都向距离食物最近的个体聚拢,继续开展搜索,循环往复直到达到找到食物的目的[18].果蝇在觅食过程的行为轨迹,如图1所示.

图1 果蝇群体觅食的过程轨迹图示[19]
1.2 FOA算法表述
标准FOA算法的主要部分为嗅觉搜索和视觉搜索两个部分,算法描述如下:
步骤1:初始化参数
初始算法的种群规模popsize,设定种群果蝇个体的寻优范围LR,因为FOA的寻优过程通过纵坐标和横坐标的二维空间搜索,设定种群中果蝇个体的初始位置为(X_axis,Y_axis);设定算法寻优过程中的最大迭代次数maxgen及寻优半径初始值RV.算法中果蝇个体的初始位置为
(1)
步骤2:开始迭代,进行寻优
步骤2.1:嗅觉搜索
果蝇个体按照固定步长更新位置,按照随机的方向和距离进行搜索,某一时刻果蝇i的位置为
(2)
步骤2.2:计算每个果蝇个体的味道浓度判定值
(3)
(4)
步骤2.3:评价当前种群的适应度函数值,计算种群中每个果蝇个体的味道浓度值Smelli,选择种群味道浓度值最大或者最小的个体为当前种群的最优个体,记录其位置和味道浓度为
Smelli=Fitness(Si),
(5)
[bestSmell,bestIndex]=max/min(Smelli).
(6)
步骤3:视觉搜索
记录步骤2.1中的最优个体的位置信息和味道浓度值,当前种群的个体向最优个体飞行并更新位置为
SmellBest=bestSmell,
(7)
Y_axis=Y(bestIndex),
(8)
Y_axis=Y(bestIndex).
(9)
步骤4:迭代寻优步骤.
重复步骤2和步骤3 .若迭代过程中有更优个体,则以新的个体的位置和味道浓度更新种群最优,否则继续嗅觉搜索过程直到达到迭代次数maxgen结束算法.
FOA在全局寻优能力方面表现突出,但存在收敛速度过快、易陷入局部最优的问题[20],对高维问题的解决能力有限[21].FOA算法中种群规模、迭代次数、寻优半径等参数的选取是影响算法性能的重要因素,研究表明增加种群规模和迭代次数可以提高算法的收敛精度,但算法耗费的时间相对增加,当种群规模、迭代次数达到一定程度时算法可能会陷入局部最优,导致收敛精度不会进一步提高[22].
2 基于云模型的改进FOA
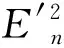
(10)
其中:μ(x)表示(0,1)之间具有平稳趋势的随机数.
在FOA中,果蝇个体的位置是随机的,果蝇个体相对于原点的距离也是随机的,决定了果蝇个体的味道浓度计算具有随机性和不确定性的特点,算法通过判断果蝇个体的味道浓度决定下一步搜索的寻优步长和方向,而味道浓度的不确定性和随机性决定了搜索步长和方向的模糊性.在FOA中没有体现味道浓度随机性和模糊性,而且在算法寻优过程中采用固定步长也使得算法在搜索效率和收敛精度上受到影响.因此,本文对FOA算法的嗅觉搜索过程进行改进,在果蝇个体位置更新时考虑味道浓度的影响,引入味道浓度因子控制算法寻优半径自适应调整,为了体现果蝇个体味道浓度的模糊性特点,以果蝇个体到原点的距离为云滴,利用正态云模型生成确定度为味道浓度参数的正态云,使得味道浓度值服从正态分布,从而使候选解在解空间均匀生成.改进后的FOA算法表述如下:
步骤1:初始化
设定算法种群规模popsieze的值、算法寻优过程中的最大迭代次数maxgen、种群果蝇个体的寻优范围LR,设置算法种群当前迭代代数g,设置果蝇个体搜索步长的自适应调整范围参数RVmin,RVmax,RVmin为搜索半径的最小值,RVmax为搜索半径的最大值,初始果蝇个体的初始位置为(X_axis,Y_axis).
(11)
步骤2:开始迭代,进行寻优
步骤2.1:嗅觉搜索
果蝇个体根据味道浓度因子动态调整搜索步长,更新位置,果蝇i的位置更新为
(12)
RVi=SFi×rand(),
(13)
(14)
果蝇个体的搜索半径由味道浓度因子SFi动态调整,当果蝇个体的当前味道浓度Si小于当前种群的平均味道浓度Savg时,味道浓度因子为搜索步长的最小值RVmin加变化量,反之则设定果蝇个体的搜索步长为最大搜索步长.
步骤2.2:计算果蝇种群的味道浓度参数
计算当前种群中每个果蝇个体到原点的距离DISTi、果蝇种群平均距离DISTavg和最大距离DISTmax,根据云模型定义可知要使用正态云模型描述味道浓度参数的模糊性与随机性,就是要以当前果蝇种群到原点的平均距离DISTi为期望,以种群到原点的最大距离和最小距离为范围(DISTmax~DISTmin)生成云滴,从而使果蝇个体的味道浓度参数体现出模糊性和随机性.计算过程为
(15)
(16)
Ex=DISTavg,
En=r1×(DISTmax-DISTavg)×2,
(17)
He=r2×En,
(18)
(19)
其中:r1、r2为控制参数.
步骤2.3:评价当前种群的适应度函数值
计算种群中每个果蝇个体的味道浓度值Smelli,选择种群味道浓度值最大或者最小的个体为当前种群的最优个体,记录其位置和味道浓度为
Smelli=Fitness(Si),
(20)
[bestSmell,bestIndex]=max/min(Si).
(21)
步骤3:视觉搜索
记录最优果蝇个体的位置和味道浓度值,当前种群的个体向最优个体飞行并更新位置为
X_axis=X(bestIndex),
(22)
Y_axis=Y(bestIndex),
(23)
步骤4:迭代寻优
若当前迭代代数g
3 改进FOA算法应用及实验结果分析
为验证改进FOA算法的有效性和算法性能,将改进后的FOA算法应用于自动组卷系统,通过与相关文献[25~26]改进的FOA算法的实验数据进行比较,从组卷的精度和效率等方面评估改进FOA算法收敛性能.
3.1 试卷的数学模型
试卷中的试题主要包含以下属性:(1)试题编号(试题的唯一标识);(2)题型编号(1-单选题,2-多选题,3-判断题,4-填空题,5-问答题);(3)试题难度系数(学生的失分率);(4)试卷区分度(区分学生水平能力);(5)考试时间;(6)题分.
将一份试卷映射为一个果蝇个体,试卷中每道试题由上述6个属性约束,构成一个属性向量(题号a1,题型a2,难度a3,区分度a4,时间a5,题分a6),含有m道试题的试卷可以看作m×6矩阵A.
其中:aij为第i道试题的第j个属性.
试卷模型的约束条件如下:

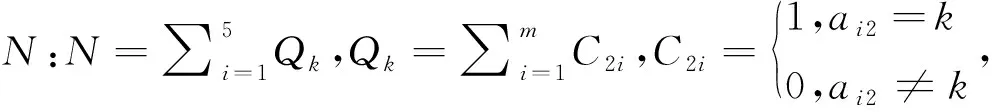

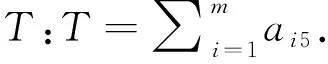
3.2 约束函数
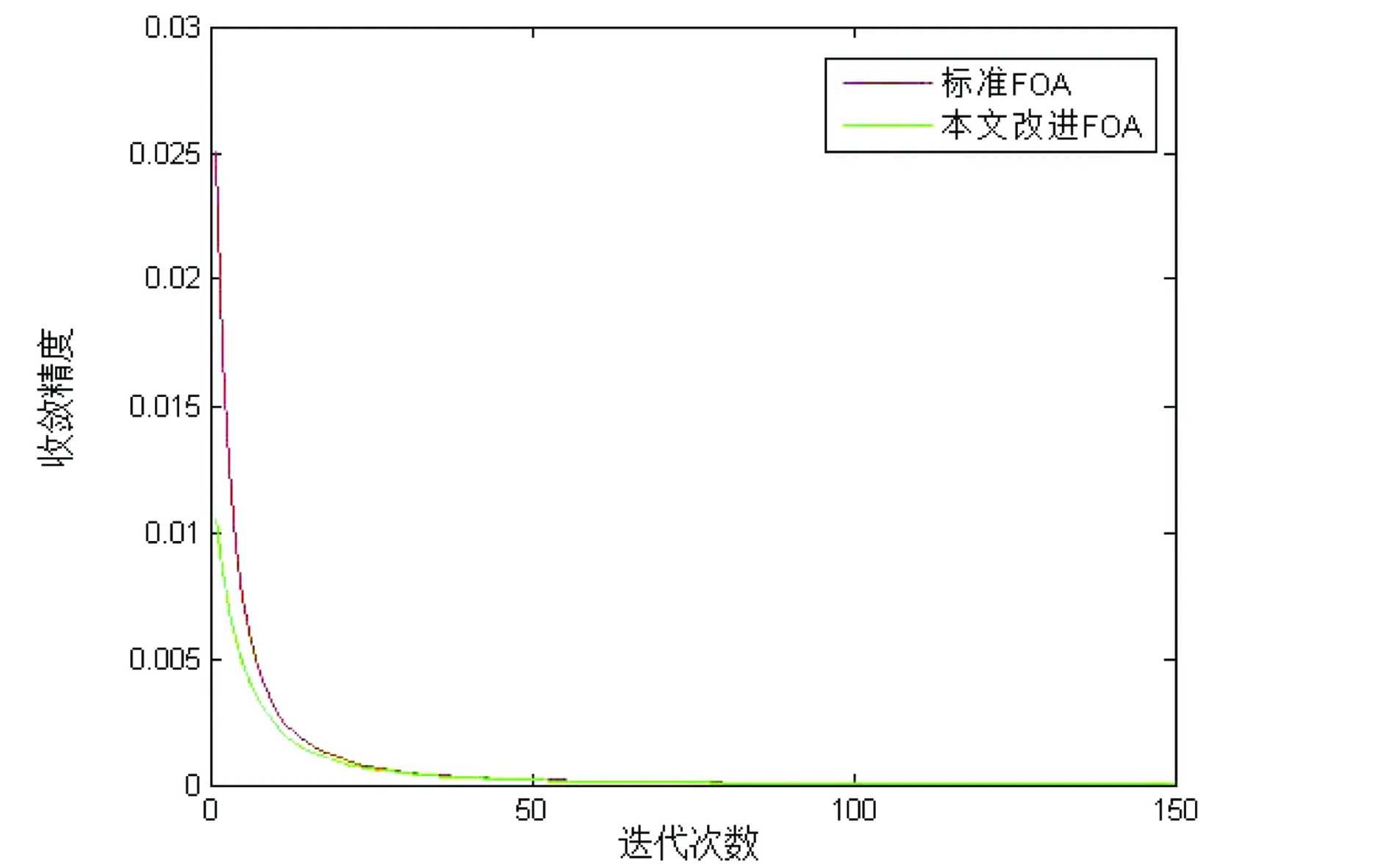
图2 标准FOA 和改进后FOA 算法收敛对比
3.3 实验结果及分析
实验过程中设置算法的种群规模为100,最大迭代次数为200,设置搜索半径的最小值和最大值为2和5.设定一份试卷为一个果蝇个体,每份试卷的试题数量分别取30、50和70,经过20次独立运行的结果,如表1所示.采用正态云模型改进后的FOA果蝇个体在寻优过程中,味道浓度因子自适应调整搜索步长,对于味道浓度值大于平均味道浓度值的个体,在寻优过程中被赋予最大搜索半径,加快了算法收敛速度;而对于味道浓度值小于平均味道浓度值的个体,在寻优过程中根据味道浓度因子被赋予自适应调整的搜索半径,提高了算法的收敛精度,因而在优化最小值Smin、平均值Smax、标准差Sst等表现出较好的效果.另外,在算法迭代过程中,以果蝇个体到原点的平均距离为期望生成云滴,使产生的可选解呈正态分布,促使算法可选解产生机制呈现出随机性和模糊性,提高算法的全局寻优能力.基于云模型的FOA算法在搜索初期,由于果蝇个体的味道浓度值赋予了较大的寻优半径,使得算法能够较快的收敛,而在搜索的后期根据味道浓度因子自适应调整步长,有效的避免了算法陷入局部最优,如图2所示.

表1 基于云模型FOA与标准FOA及文献改进FOA收敛精度对比(popsize=100)
4 总 结
本文将云模型理论中的正态云模型应用于FOA的优化改进,在算法的嗅觉搜索阶段,引入了味道浓度影响因子,动态自适应调整果蝇个体的寻优步长,提高了算法的收敛速度,用正态云模型生成味道浓度参数云滴,改进算法最优解的产生机制,体现了算法的随机性和模糊性,提高了算法的收敛精度,防止算法陷入局部最优.从算法在自动组卷系统的应用表明改进后的算法在收敛速度、收敛精度方面都有所提高.
