变声速弹性沉积层下压缩波与剪切波的耦合影响∗

刘亚琴3) 杨士莪1)2)3) 张海刚1)2)3)† 王笑寒3)

1)(哈尔滨工程大学,水声技术重点实验室,哈尔滨 150001)

2)(哈尔滨工程大学,海洋信息获取与安全工业和信息化部重点实验室,哈尔滨 150001)

3)(哈尔滨工程大学水声工程学院,哈尔滨 150001)

(2018年8月27日收到;2018年9月27日收到修改稿)

1 引 言

海洋中的声传播是一个极其复杂的过程,浅海中声传播相较深海来说更为复杂.因为在浅海波导中,声波的传播受到海底界面的影响更严重.在实际的海洋环境中,海底沉积层中的声速(压缩波声速和剪切波声速)一般是随深度变化的[1].多数的文献和实验结果表明,疏松的海洋沉积层中剪切波声速一般随深度连续增加,并且声速正比于zυ(z以海水与沉积层交界面为基准)[2−7].压缩波与剪切波声速随深度变化的特征意味着声波与海底相互作用的性质在低频和高频时是截然不同的.对于大入射角、远距离的传播问题,海底的高频响应可以将海底当作流体来处理[8].Liu等[9,10]在有液态沉积层(密度随深度为广义指数变化,压缩波声速为常数、n2线性或平方反比形式)的环境下,研究了粗糙海底的平面波散射声场的空间功率谱密度以及平面波反射系数,为海底声学的研究提供了典型的环境模型.但是其研究没有考虑沉积层中的剪切特性.如果能量穿透沉积层透射在沉积层-弹性基底界面上,那么流体模型就不再适用了[8].弹性体中能量的向上折射导致压缩波与剪切波之间的相互耦合、转换.由于声速的变化而导致的压缩波与剪切波之间的耦合将会对声场产生怎样的影响成为本文研究的内容.

Ewing等[11]给出了在各向同性的非均匀介质中的波动方程.在接下来的有关研究中,一些学者(如Karal,Hook,Scholte)[12−14]在研究非均匀弹性介质中的波动方程时,同时考虑了剪切波声速、压缩波声速以及密度的变化,得到的结果极其复杂.为了能够使问题简化且得到更加清晰的物理意义,接下来的有关变参数弹性层的研究主要包括两个方向:一是在某些特殊情况下给出非均匀弹性层中的解析解或近似解析解.Gupta[15]对密度为常数,拉梅常数的变化形式为λ/λ1= µ/µ1=(1+bz)2(这里λ1,µ1和b为常数)的沉积层环境进行了分析,得到了P波与S波的去耦合方程,并且得到此种情况下的反射系数;Hall等[7]提出了半解析的反射模型,考虑了由于剪切模量随着深度变化(G(z)∝zp)引起的耦合效应,导出了势函数P和势函数S的弱耦合方程、利用Born近似求解势函数P的方程;另一个主要的研究方向是忽略剪切波及压缩波声速梯度引起的耦合.Vidmar和Foreman[16]提出了用传递矩阵的方法计算平面波反射系数的模型,其中弹性沉积层的密度、剪切波声速、压缩波声速以及衰减可以任意变化.Westwood等[17]基于简正波理论提出了ORCA模型,可以计算具有多层弹性环境下的声场,且层中的剪切波速度和压缩波速度可以是常数也可以是n2线性的,但是在弹性层中,P波和S波的势函数满足的波动方程忽略了耦合.

上述研究在处理弹性沉积层声速变化的环境时,一般选择忽略声速变化引起的耦合,虽然Hall考虑了剪切模量随深度变化引起的耦合并给出了半解析的反射模型,但是其并没有分析耦合对反射的影响.Fryer[8]用数值解法研究了由于压缩波、剪切波声速梯度引起的P-SV耦合的反射率.通过比较总反射率与忽略耦合得到的部分反射率,得到了P-SV耦合的反射率,并研究了这种耦合对反射率的影响.此外,通过平面波响应函数清楚地揭示了耦合的主要结果是剪切向压缩运动的转换.但是数值解法的计算时间会随着沉积层厚度的增加而增加.考虑弹性沉积层声速引起的耦合效应,本文求解弹性沉积层某种声速变化形式下声场势函数的近似解析解,进而研究此种耦合对低频声场的影响以及声学参数对耦合效应的影响程度.

本文的内容主要包括:第2部分是声场建模,重点研究变参数弹性沉积层中压缩波与剪切波本征函数的近似解析解;第3部分仿真验证本文方法的有效性,研究剪切波、压缩波的耦合对低频声场(水中声压场以及沉积层中质点位移场)的影响;第4部分研究弹性沉积层中声学参数对耦合的影响;第5部分是实验数据处理;最后一部分是结论.

2 声场建模

考虑流体层中单频点声源激发的声场问题,在柱坐标系下建立如图1所示的环境模型.时间因子为exp(−jωt),为了方便,在以下的推导过程中省略时间因子.

图1 环境模型Fig.1 .Environment model.

模型中,声源位于深度为H0,密度与声速分别为ρ0和c0的均匀流体层中,点声源的坐标为(0,zs);弹性沉积层厚度为(H1−H0),且沉积层中密度、压缩波、剪切波声速分别为ρ1,c1(z),b1(z);半无限弹性海底中密度、压缩波、剪切波声速分别为ρ2,c2,b2.各介质层中压缩波与剪切波势函数分别为φ0;φ1,ψ1;φ2,ψ2.

文献[18]中已经证明,在柱坐标系下,ψ1和ψ2只有沿θ方向的分量,记θ方向上的分量分别为ψ1和ψ2,这样,矢量势函数就可以转化为标量势函数,将这些标量势函数用Fourier-Bessel积分表示.记:

参看文献[18,19],Z0(z,ξ),Z2(z,ξ)和G2(z,ξ)的表达式为:

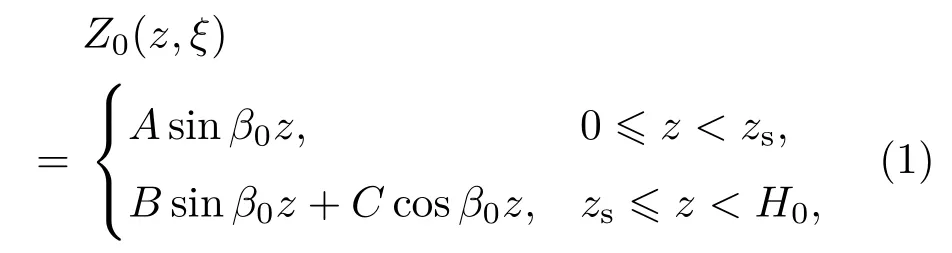
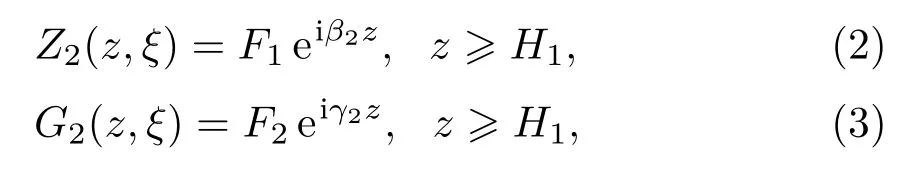
在变参数弹性沉积层中,压缩波与剪切波声速随深度变化将会引起二者之间的耦合,具体表征为函数Z1(z,ξ)和G1(z,ξ)形成耦合方程组.此前没有相关文献求解此种环境,本文建立、求解耦合方程组过程如下.

在变参数弹性介质中,φ1,ψ1所满足的波动方程为[20]:

其中

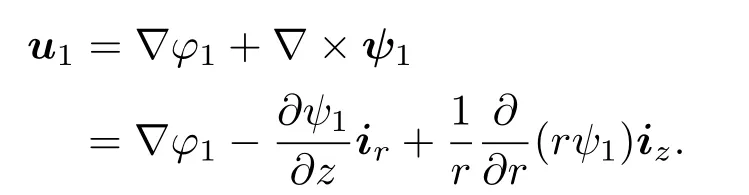
对波动方程(4)式分别取散度和旋度,进行化简整理(具体过程详见附录A),可得

在变参数弹性介质中Z1(z,ξ)和G1(z,ξ)所满足的方程为:

其中

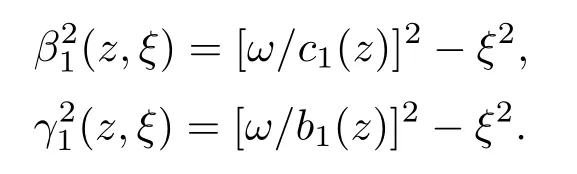
观察(7)和(8)式组成的耦合方程组,考虑特殊情况σ=0时,即横波声速不随深度变化,此时方程组(7)和(8)式为:

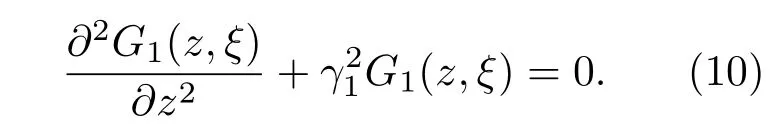
此时,无论纵波声速如何变化,横纵波之间无耦合.但在一般情况下,б=0,横纵波之间发生耦合,此前一般都是利用数值处理方法来处理(7)和(8)式,随着沉积层厚度的增加,数值处理方法计算时间增加.本文提出一种近似解析方法求解耦合方程(7)和(8).考虑到实际情况中α,σ均很小、其二阶小量要远小于α,σ的值,在求解过程中忽略有关二阶小量.

和(8)记为:

对方程(11)和(12)分别进行逐次微分,可得

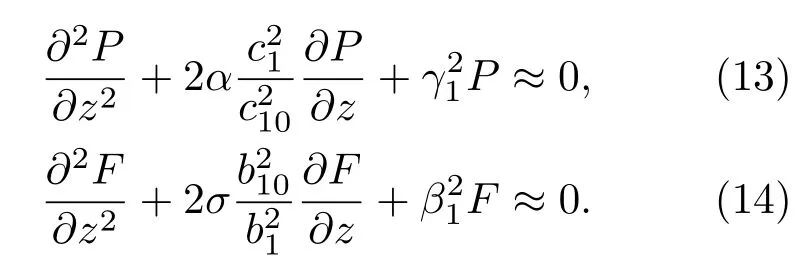
至此,耦合方程组转化成了非耦合方程(13)和(14).根据方程(13)和(14)可求得函数P(z,ξ)和F(z,ξ),进而可求得本征函数Z1(z,ξ)和G1(z,ξ)的表达式.

方程(13)和(14)均是齐次微分方程,可通过变数代换的方法将其转化为可解情况[21].具体求解过程在附录B中给出,方程的解为:

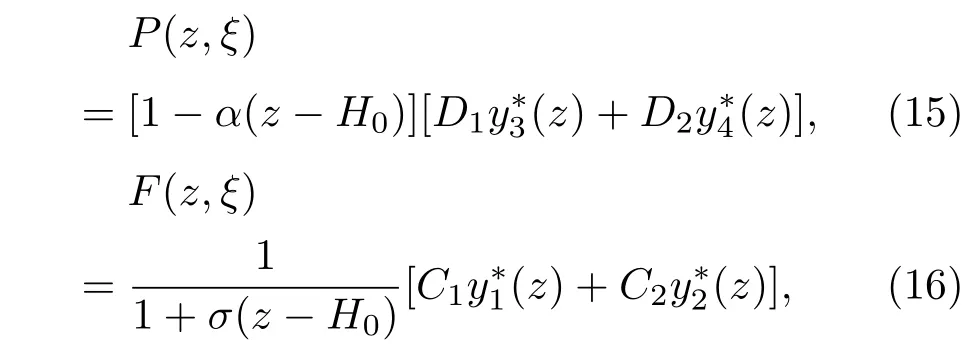
其中

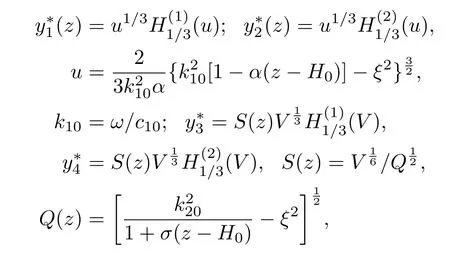
将P(z,ξ)和F(z,ξ)的表达式代入方程(11)和(12),可得Z1(z,ξ)和G1(z,ξ)的表达式为:

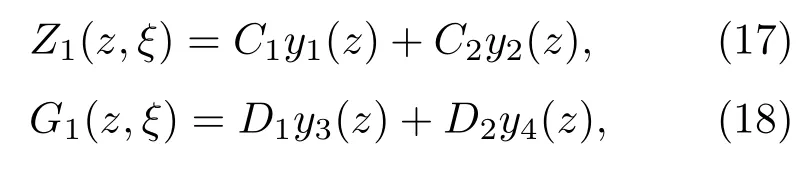
其中

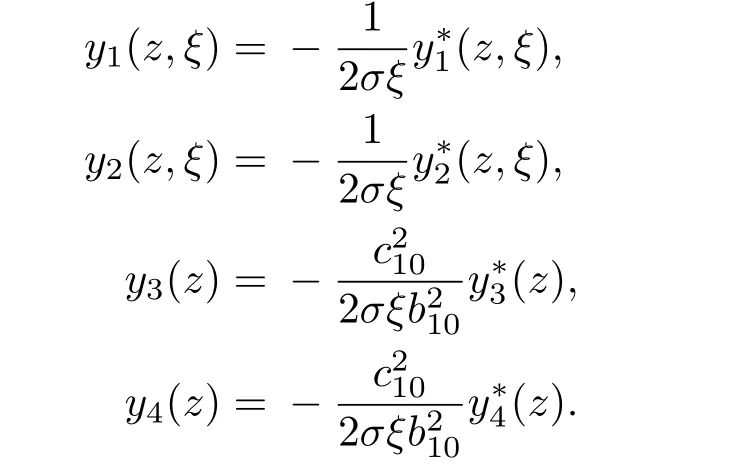
从Z1和G1的表达式可以看出,剪切波声速的σ值将会影响Z1的值,而压缩波声速中α对G1的影响在G1表达式中没有体现,是由于在求解G1表达式的过程中,忽略了(B1)方程(详见附录B)中α的二阶小量.这里反而是c10的值影响G1的表达式,但是在考虑是否引起压缩波与剪切波之间的耦合,究其原因是由于声速的变化,所以c10的值的改变不会对耦合产生影响.

根据点源条件、液/固边界条件和固/固边界条件,可得诸待定系数所满足的方程组为

其中

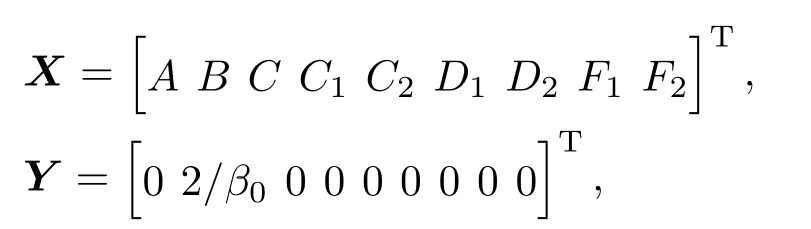
[aij]9×9的具体表达式见附录C.求解(19)式可得诸系数的值,进而得到势函数的具体积分表达式.

进一步求势函数的值可以用快速傅里叶变换(FFT)方法.以水中势函数φ0(r,z)为例,φ0(r,z)的积分表达式为[22]

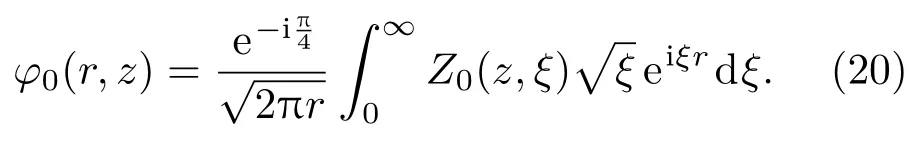
利用FFT变换就可得到势函数的近似表达式:

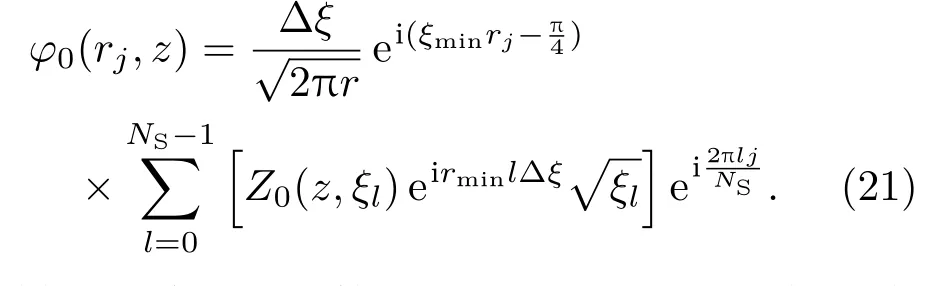
同样的方法可以计算出沉积层和半无限弹性海底中势函数的表达式.

3 压缩波与剪切波的耦合影响

3.1 耦合对水中声压场的影响

为验证本文方法(考虑压缩波与剪切波之间的耦合)的有效性,以COMSOL软件仿真得到的声压传播损失作为参照.此外,为了分析耦合对水中声压场的影响,仿真非耦合情况下的声压传播损失.在仿真验证之前,先简单介绍非耦合情况与耦合情况声场计算的不同.

1)未考虑耦合的弹性沉积层中,Z1(z,ξ)和G1(z,ξ)所满足的方程(7)和(8)式退化为:

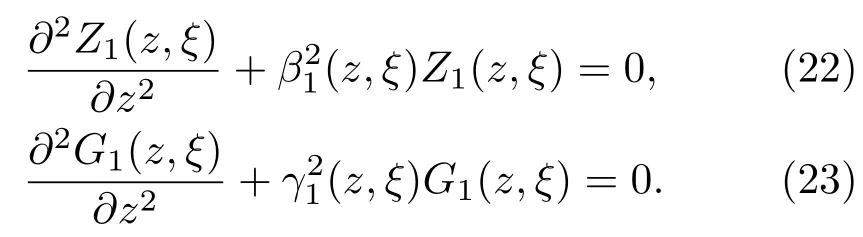
2)非耦合弹性沉积层中的法向应力和切向应力的表达式相较于耦合情况分别缺失项.

在仿真过程中,以具体的环境(如表1所列)为例,取声源频率f=25 Hz,声源深度Zs=100 m,接收深度Zr=150 m.

图2(a)和图2(b)是仿真环境I下COMSOL软件和耦合以及非耦合情况下计算出来的声压传播损失.

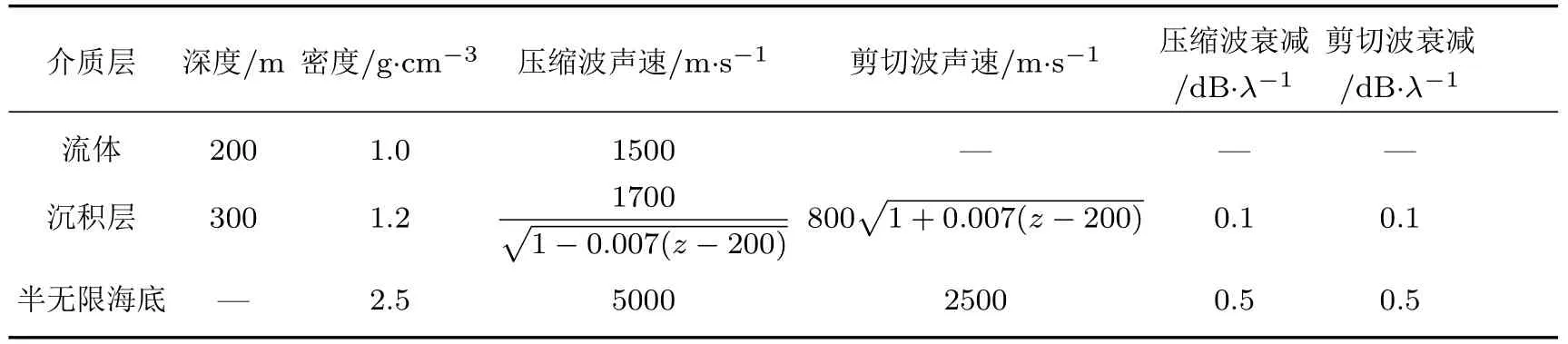
表1 环境I的声场参数Table 1 .Sound f i eld parameters of the ocean environment I.

从图2(a)中可以看出,本文方法计算出来的传播损失与COMSOL软件计算出来的传播损失基本一致,只有在某几处距离上有些偏差,产生这些偏差的原因是因为本文方法在推导过程中忽略了α,σ的二阶小量,且快速场方法在计算的过程中距离是抽样间距(抽样间距∆r=2π/(M∆kr),其中∆kr是波数抽样间距,M是计算的点数).仿真结果表明了本文方法的有效性.非耦合与COMSOL软件计算的传播损失曲线在近距离处基本符合,但是随着距离的增加,两条曲线有较大的偏差,如图2(b)所示.图3为耦合和非耦合算法中积分核函数Z0(z,ξ)的幅度沿实水平波数轴的分布图.

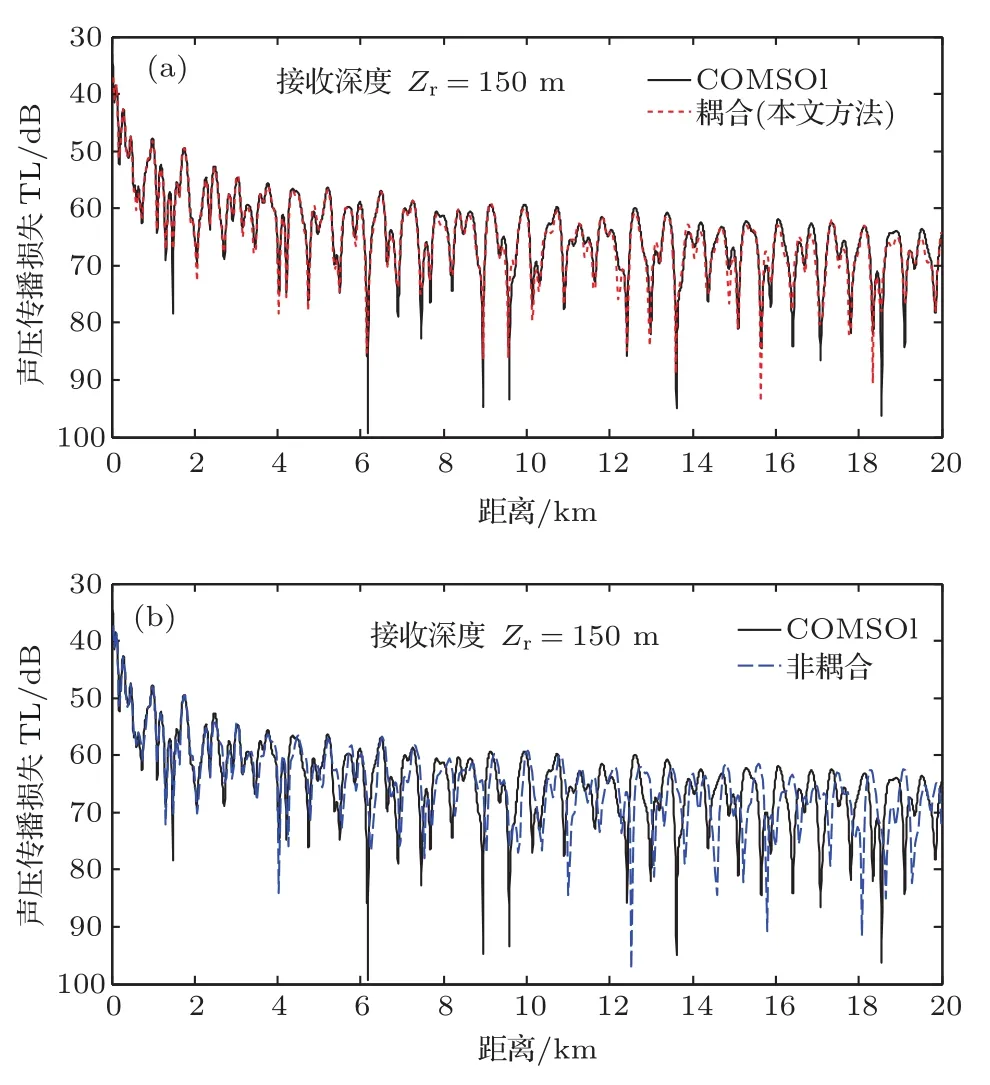
图2 声压传播损失对比图 (a)耦合情况;(b)非耦合情况Fig.2 .Comparison chart of TL curves for sound pressure propagation loss:(a)In coupled case;(b)in uncoupled case.

由于沉积层中压缩波、剪切波衰减均为0.1 dB/λ,故在实轴上不存在极点,但是相应的极点明显地表现为极陡的峰(极陡的峰对应的水平波数可以理解为简正波理论中的本征值).从图3中的局部放大图可以看出,两种方法计算的陡峰对应的水平波数(即本征值)有些微变化,具体值如表2所列.从表2中可以看出,考虑耦合分别导致3处陡峰处0.21%,0.25%,0.14%的本征值变化,本征值的改变导致水中声场的变化.

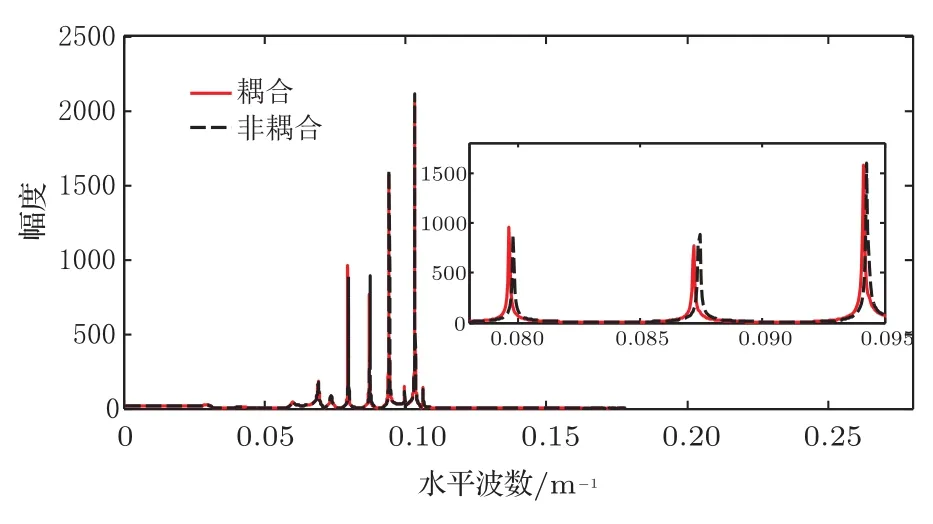
图3 积分核函数Z0(z,ξ)的幅度沿实水平波数的分布图Fig.3 .Distribution of amplitude of integration kernel Z0(z,ξ)along real horizontal wavenumber axis.

表2 耦合与非耦合下陡峰对应的水平波数Table 2 .Horizontal wave numbers corresponding to steep peaks under coupled and uncoupled conditions.

图4(a)为耦合与非耦合情况下计算出来的传播损失与COMSOL软件仿真的传播损失之差,图4(b)和图4(c)分别为在0—5 km和5—20 km距离范围内,耦合、非耦合两种情况下计算的传播损失与COMSOL软件仿真的传播损失之差绝对值的直方图.其中红色代表耦合情况、蓝色代表非耦合情况.在0—5 km距离范围内,耦合与非耦合两种算法的传播损失偏差均偏小,但是考虑耦合,偏差绝对值主要集中在0—2 dB(95.75%),而非耦合的偏差绝对值主要集中在0—5 dB(94.32%);在5—20 km距离范围内,考虑耦合时传播损失偏差绝对值主要集中在0—3 dB(90.1%),最大差值也仅为11.73 dB,而非耦合情况下,偏差绝对值在3—12 dB范围内的数据所占比例达到49.99%,在12 dB误差以上的数据也达到了9.68%的比重.对比图2、图3以及图4的仿真结果,表明在此种环境,压缩波、剪切波之间的耦合影响水中声场,若忽略耦合,在5—20 km距离范围内,传播损失计算偏差绝对值最大可达35.41 dB,声场计算偏差较大.

在运行环境一致的情况下,本文方法计算时间要远小于COMSOL软件计算时间.以环境I为基准,改变沉积层厚度而其他参数不变时,本文方法计算时间与COMSOL软件计算时间如表3所列.

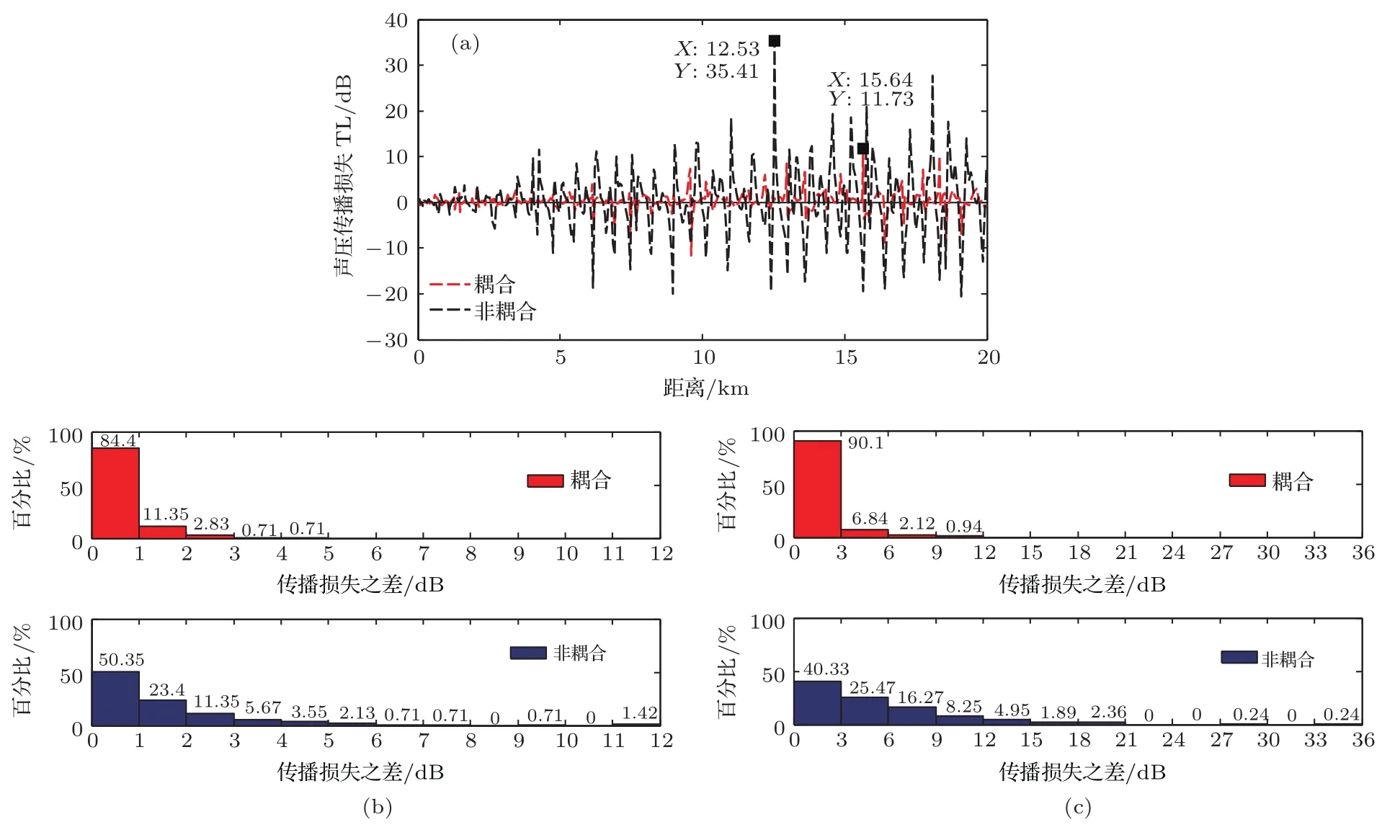
图4 (a)传播损失之差;(b)0—5 km的直方图;(c)5—20 km的直方图Fig.4 .(a)Dif f erence of TLs;(b)histogram in the range of 0 to 5 km;(c)histogram in the range of 5 to 20 km.

表3 计算时间对比表Table 3 .Comparison table of calculation time.

3.2 耦合对沉积层中质点位移场的影响

沉积层中质点水平位移、垂直位移的表达式:

其中urc,uzc是压缩波产生的水平位移与垂直位移;urs,uzs是剪切波产生的水平位移与垂直位移.其中:

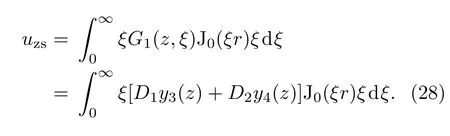
(25)—(28)式表明,压缩波与剪切波产生的水平位移与垂直位移是Z1(z,ξ),G1(z,ξ),(z,ξ)和(z,ξ)的积分函数.

仿真环境如表4所列,声源频率f=25 Hz,声源深度Zs=100 m.图5给出了距离为3811 m时,质点水平位移与垂直位移随深度的变化.其中红色实线代表耦合算法下压缩波与剪切波共同作用下产生的水平位移,黑色实线是耦合算法下只计算剪切波产生的水平位移,蓝色实线是耦合算法下只计算压缩波产生的水平位移;相对应的虚线代表的是非耦合情况.图5表明,压缩波、剪切波以及二者共同作用产生的水平位移、垂直位移在耦合和非耦合情况下均不同,即耦合改变沉积层中质点的位移场.究其原因,是由于耦合与非耦合情况下本征函数Z1(z,ξ)和G1(z,ξ)及其导数(z,ξ)和(z,ξ)的不同.图6给出了本征值对应下本征函数及其导数随深度的变化.耦合与非耦合情况下,压缩波、剪切波以及二者共同作用产生的水平位移、垂直位移由于本征函数及导数的不同而不同.

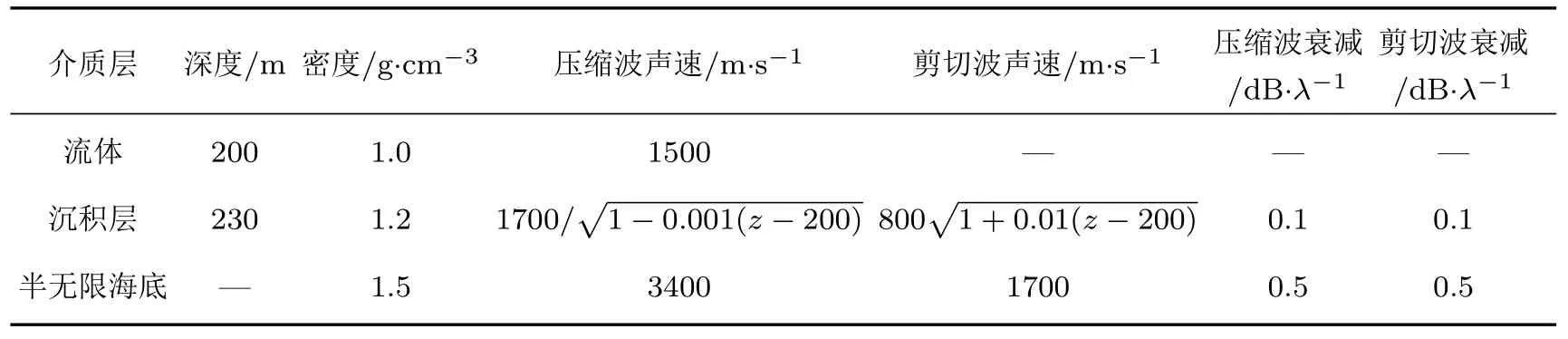
表4 环境II的声场参数Table 4 .Parameters of the ocean environment II.

图5 水平位移与垂直位移随深度变化Fig.5 .Horizontal and vertical displacement according to depth changes.

图6 耦合与非耦合情况下Z1(z,ξ),G1(z,ξ)及其导数随深度的变化Fig.6 .Functions Z1(z,ξ),G1(z,ξ)and derivative functions vary with depth in coupled and uncoupled cases.

图5表明,耦合和非耦合情况下,剪切波产生的水平位移、垂直位移曲线分别与共同作用产生的水平位移、垂直位移曲线类似,随深度变化有两个极值;压缩波产生的水平位移、垂直位移曲线随深度单调变化.可以看出,剪切波在水平位移和垂直位移的产生中起主导作用.从urc,uzc,urs,uzs的表达式(25)—(28)看出,压缩波产生的位移是y1(z),y2(z),(z),(z)的积分函数,剪切波产生的位移是的积分函数.图7给出不同水平波数kr(即ξ)时,这些被积函数随深度的变化图.在kr值相同时,y3(z),y4(z)的值要远大于的值大于y1(z),y2(z)的值.所以合成的垂直位移以及水平位移是y3(z),y4(z)以及起主导作用,即剪切波起主导作用.从图7中可见,随深度的变化主要有两种,一种是有两个极值点,另一种是只有一个极值点,故合成的水平位移、垂直位移随深度的变化也应该是这两种形式之一.

图7 位移被积函数随深度的变化Fig.7 .Changes of integrand of displacement according to depth.

4 沉积层参数对耦合程度的影响

弹性沉积层中压缩波与剪切波声速随深度的变化引起二者之间的耦合,进而对声场产生影响,所以这里仅考虑参数压缩波声速平方倒数的梯度α和剪切波声速平方的梯度σ对耦合程度的影响.这里的耦合程度表现为耦合与非耦合情况下传播损失的差值大小.仿真环境如表4所列,改变参数α,σ的取值,其余参数不变.参数α,σ的取值如表5所列.仿真过程中声源频率f=25 Hz,声源深度Zs=100 m,接收深度Zr=30 m.图8给出α,σ的不同取值时耦合与非耦合情况下声压传播损失曲线.图9和图10分别给出了α,σ不同取值时(表5中编号(a)—(c)和编号(d)—(f))耦合与非耦合情况下5阶本征波数的结果.图9表明,当σ值保持不变、α值增大时,除了α=0.1时非耦合的某阶本征波数值大于耦合情况,耦合与非耦合算法计算出来的本征波数值相同.在α值的增大过程中,考虑耦合对本征波数值的改变非常小,这也解释了图8(a),图8(b)和图8(c)中耦合与非耦合算法计算出来的传播损失曲线基本一致的原因.图8(a),图8(b)和图8(c)以及图9表明,弹性沉积层中压缩波声速中的α值对耦合影响较小.图10表明,当α值保持不变、σ值增大的过程中,考虑耦合在一定程度上改变了本征波数的值,导致耦合与非耦合算法计算出来的传播损失曲线差异增大,如图8(d)—(f)所示.图8(d),图8(e)和图8(f)以及图10表明剪切波声速中的σ值对耦合影响较大.图8、图9和图10表明,弹性沉积层中剪切波声速中σ值对耦合的影响程度大于压缩波声速中α值的影响程度.

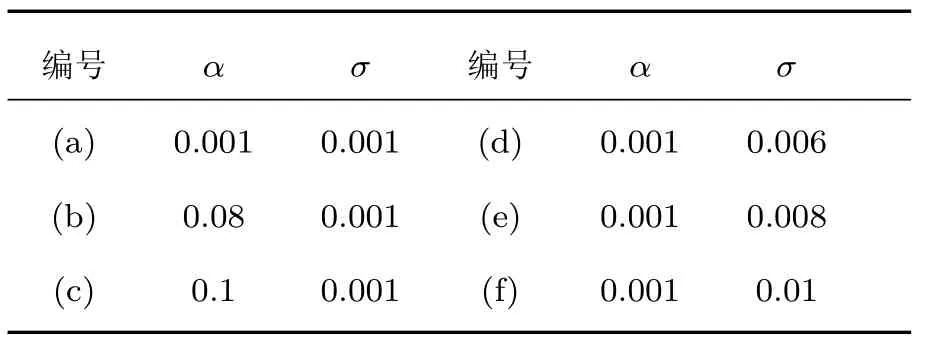
表5 声场参数α,σ的取值Table 5 .Value of sound f i eld parameter α,σ.

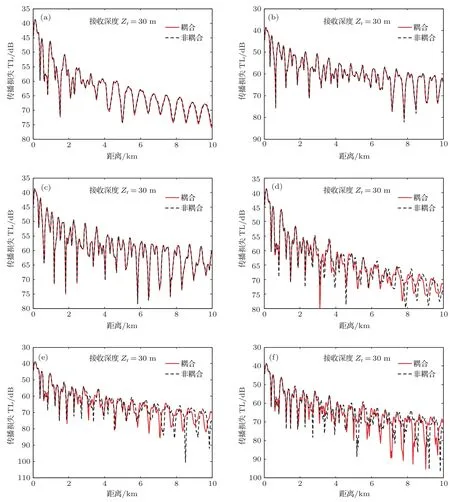
图8 α,σ取值不同时耦合与非耦合情况下的传播损失 (a)α=0.001,σ=0.001;(b)α=0.08,σ=0.001;(c)α=0.1,σ=0.001;(d)α=0.001,σ=0.006;(e)α=0.001,σ=0.008;(f)α=0.001,σ=0.01Fig.8 .Transmission loss of coupling and uncoupling when α,σ changes:(a)α =0.001,σ =0.001;(b)α =0.08,σ=0.001;(c)α=0.1,σ=0.001;(d)α=0.001,σ=0.006;(e)α=0.001,σ=0.008;(f)α=0.001,σ=0.01.

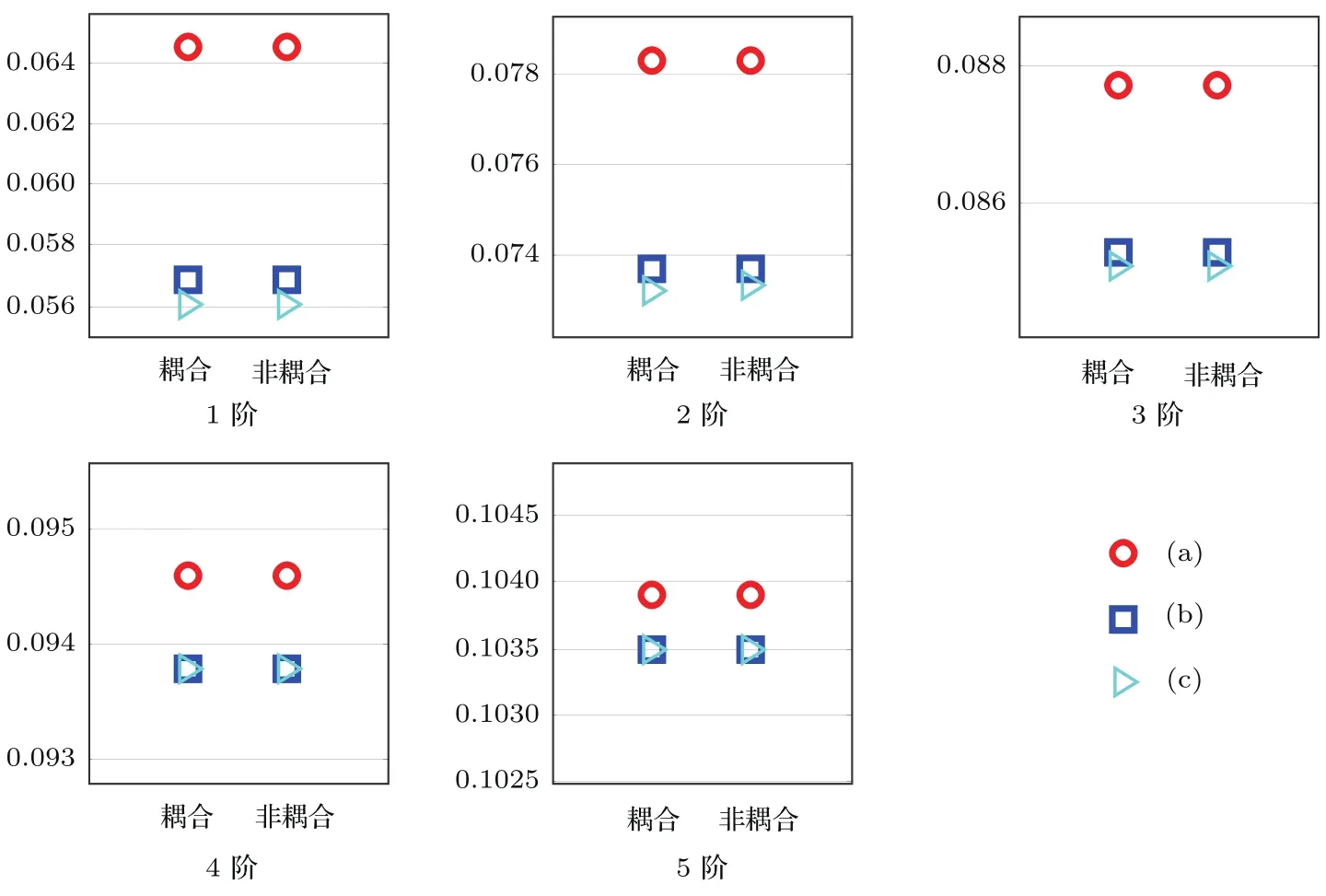
图9 耦合与非耦合情况时5阶本征波数结果 表5中编号(a),(b)和(c)三种情况时本征波数结果Fig.9 .Results of eigenwave number in three cases of Tab.5(a),(b)and(c).

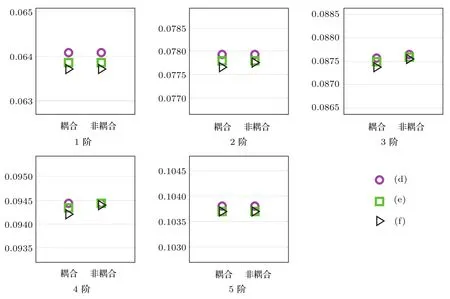
图10 耦合与非耦合情况时5阶本征波数结果 表5中编号(d),(e)和(f)三种情况时本征波数结果Fig.10 .Results of eigenwave number in three cases of Tab.5(d),(e)and(f).

5 实验数据验证

2018年1月,在青岛某海域进行了声传播特性的实验研究.一艘渔业运输船作为发射船,两条垂直阵列作为接收设备.发射船从远处向接收设备行驶,航行过程中的辐射噪声作为本次实验的目标声源.发射船行驶过程中进行GPS记录.实验海区深度约25 m,海底平坦.查阅该区海图可知沉积层类型为砂-粉砂-黏土.对于黏土、粉砂和砂质沉积物,压缩波和剪切波声速不是恒定不变[23,24].故在声场建模中,假设海洋环境如图1所示.参数的获取首先根据实验海区海底性质以及文献[23,24]中给出的该类海底参数的可能范围,然后进行参数反演得到结果.

目标船有多条线谱,选取326 Hz的线谱,对其进行传播损失的计算.使用的数据来自于1号垂直阵列上海底地震波拾振器(ocean-bottom seismometer,OBS)设备的声压传感器接收的数据.OBS被放置于海底附近处.

图11(a)表明:实验结果与耦合理论计算出来的传播损失曲线趋势基本一致.图11(b)表明:未考虑耦合时计算出来的传播损失与实验结果在某些距离处有明显的趋势差异(用黑色椭圆标记).对比图11(a)和图11(b)的结果,在实际海洋环境建模,疏松沉积层中将剪切波声速假设成随深度变化并考虑由此引起的耦合能够更好地符合实际情况.

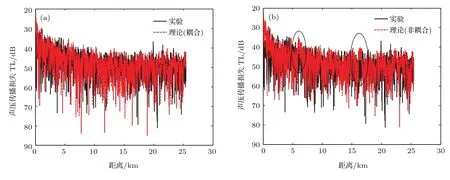
图11 声压传播损失对比图 (a)耦合情况;(b)非耦合情况Fig.11 .Comparison chart of TL curves for sound pressure:(a)In coupled case;(b)in uncoupled case.

6 结 论

针对弹性沉积层典型声速变化环境,求解出压缩波与剪切波本征函数的近似解析解,并分析了由于压缩波、剪切波声速随深度变化引起的耦合效应对低频声场(水中声压场、沉积层质点位移场)的影响,主要结论如下.

1)压缩波与剪切波之间的耦合导致本征值减小,耦合对水中近场声场计算影响较小,但是对远场声场影响较大,考虑耦合可以提高远场声场预报精度.

2)弹性沉积层中剪切波声速平方的梯度σ值是压缩波与剪切波耦合的决定性因素,当剪切波声速不随深度变化(即σ=0),压缩波与剪切波之间无耦合.仿真结果表明,σ值对耦合的影响程度随σ值增大而变大,且σ值对耦合影响程度比压缩波声速平方的倒数的梯度α值大.

3)压缩波与剪切波之间的耦合导致沉积层中本征函数Z1(z,ξ),G1(z,ξ)及其导数的变化,由于沉积层中压缩波、剪切波以及二者共同作用产生的水平位移、垂直位移为本征函数及导数的Fourier-Bessel积分,所以耦合与非耦合情况下沉积层中质点位移场不同.在仿真环境下,沉积层中压缩波与剪切波共同作用形成的水平位移与垂直位移随深度的变化曲线与剪切波单独产生的水平位移、垂直位移曲线相类似,剪切波在此过程中起主要作用.

附录A

为了推导方便,记:

对波动方程(4)式分别取散度和旋度,可得:

因为:

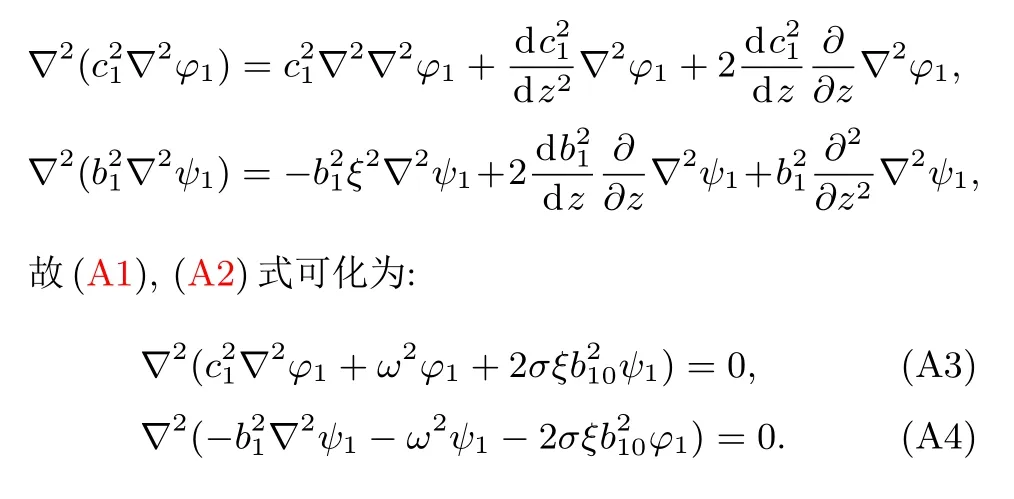
附录B

其中:

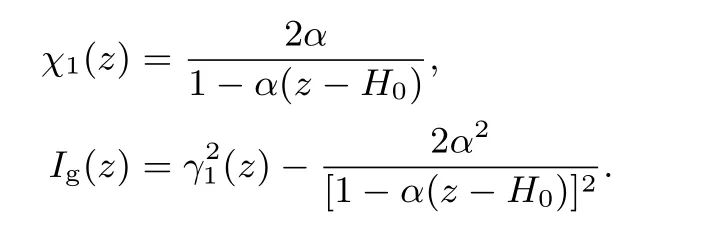
忽略α2项,则

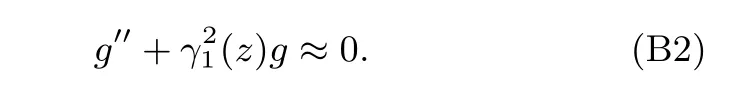
则P(z)的表达式为

附录C