浅谈《高等数学》选择题对学生思维品质的训练

马建珍

（邢台学院数学与信息技术学院，河北邢台 054001）

高等数学是非数学专业，如理科、工科、经管类等专业的重要基础课，在日常的高等数学教学中，教师大多较重视理论部分的教学，课本上的习题也更多的是计算题和解答题，选择题几乎没有。但这类题目一直以来都是高等数学各层次考试中的主要题目类型之一，也是考试中丢分率较高的，很多学生感觉这类题目做起来较难，没有所谓的“解题规律”可找。选择题具有干扰因素多、灵活多变、涉及到的知识面广、综合性强等特点，通过加强选择题的训练，一方面加深学生对相关理论知识的理解，提高解题能力；同时通过训练来培养学生的思维品质，提升学生思维的广阔性、灵活性、深刻性、敏捷性等，不断提升学生的逻辑思维能力和综合解决问题的能力。

1 加强选择题教学，训练思维的敏捷性

例1：下列各式正确的是 ()。

分析：首先要弄清楚题目考查的是哪一个知识点，表面看来是考查定积分的计算，但题目呈现的形式只是一个障眼法，实际上是考查定积分的几何意义，故题目涉及的定积分即是相应的曲边梯形的面积。由此思路切入进行解答，便可迅捷地做出判断。

A选项，由定积分的几何意义得知左侧的定积分是“正面积”，右侧的积分是“负面积”，两个“面积值”相等，符号相反，所以此选项错误。

B选项，因为此曲边梯形整个都在横轴的上方，其面积是“正面积”，不可能为零，所以此选项错误。

C选项，因为此曲边梯形在横轴的上方和下方的面积相等，在横轴的上方的面积是“正面积”，下方的面积是“负面积”，两个“面积”绝对值相等，符号相反，所以此选项正确。

D选项，根据定积分的几何意义，此定积分的值是以原点为圆心，以3为半径的圆在横轴的上方半圆面积，故积分值应该是所以此选项错误。

此题目若按照常规思路去计算每一个定积分，会耗费较多的时间，尤其是选项D，计算此定积分要利用三角换元来计算，过程较繁琐。但是题目的设计者本意显然并不是要考查定积分的计算。此类题目考查学生是否能够敏锐地抓住问题的本质，理解题目设计者要考查的是哪一个知识点，快速准确地做出反应并果断地解决问题。所以在日常教学的训练时，评价做题好与差的标准不仅是答案的正误，同时要重视解题方法的优劣和解题时间的长短。

在日常教学中，对于每个选择题要求学生找出最优解，以达到提高解题速度与准确度的目的。当然，思维敏捷性的提高有待于基础知识、基本技能、基本方法的熟练掌握。

2 加强选择题教学，提高灵活应变的能力

A．f（0）是f（x）的极小值

B．f（0）是f（x）的极大值

C.（0，f（0））是y＝f（x）的拐点

D．以上判断都不正确

正确答案应选A。

理由：已知从 而 f''（x） ＞0， 而 f''（x）

故f（0）是f（x）的极小值，所以正确答案是选项A。

这类综合性题目在一般的教材和参考资料上并不常见，对初学者来说确实有一定的难度。此题是一个综合运用极限理论和微分学知识解决问题的典型例子，考查学生综合运用不同板块知识解决问题的能力，考查学生是否具有改变常规思维角度，摆脱常规繁杂的思路，寻找较佳解决途径的思维品质，这就是思维的灵活性。

选择题设疑布障，新颖多变，适合应变能力的训练；又因其小巧，无须繁杂推演，便于学生改变思路，因此可以用来训练学生思维的灵活性。

3 加强选择题教学，训练思维的广阔性

例 3：曲线积分 ∮L（x2ycosx+2xysinx-y2ex）dx+（x2sinx-2yex）dy=______。

其中L为正向星形线：

分析：上述积分是第二类曲线积分，其计算方法有三种，可以在教师的指导下引导学生做如下分析：

（1）直接按第二类曲线积分的计算公式化为定积分来计算；

（2）利用第二类曲线积分是否与路径有关的相关结论来计算；

（3）利用格林公式化为二重积分来计算。

本题目是综合考察第二类曲线积分及其相关知识点的。实际上，设函数 P（x，y）=x2ycosx+2xysinx-y2ex，Q（x，y）=x2sinx-2yex，

也可以根据

得出第二类曲线积分与路径无关，从而沿区域内任意闭曲线的曲线积分为零。

即有

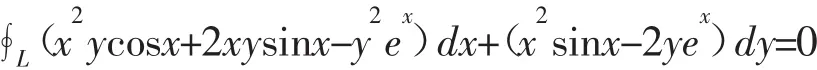
所以正确答案应选B。

按照上述两种思路解答此题，已知的星形线方程这个条件就是一个“多余”的已知条件。如果直接按第二类曲线积分的计算公式化为定积分来计算就要繁杂许多，题目设计者显然要考查的并不是第二类曲线积分的计算这个知识点。

思维的广阔性包括从不同的角度，运用多方面的知识来思考问题的思维品质。

日常教学中可选用一题多解的题目来训练学生从不同角度来思考问题，即思维的广阔性。

4 加强选择题教学，训练思维的系统性及深刻性

例4：下列各式正确的是 ()。

分析：本题目综合考查积分学和微分学的相关知识。

选项A和B考察的是微分学中的导数概念。考查学生是否能够深刻理解导数概念的本质，从概念来说导数是函数的增量与自变量增量之比的极限。而增量的形式是多种多样的，可正可负，其形式可以是（△x，h），也可以是（-△x，h）。

C选项，因为等式的左边是先求一个定积分再求导数，因为定积分的结果是一个常数，而常数的导数为零。故先求一个定积分再求其导数结果应该是零，不可能是函数f（x）。此选项是综合考查微分学中的求导与积分学中的定积分概念的，从概念本质来说，定积分是一个积分和的极限，是一个常数，而由微分学的求导公式得知常数求导的结果是零，所以此选项错误。

D选项，此选项是考查定积分中的牛顿-莱布尼兹公式，根据公式等式左边的定积分应该等于其原函数在此区间上的函数值的差，即，不可能是f（b）-f（a），所以此选项错误。

通过对以上错误选项的剖析，加深了学生对导数概念、定积分概念以及牛顿-莱布尼兹公式的深刻理解，在求解相关问题时不会再出现理解偏差。

像这类一道选择题涉及好几个知识点的题目，在考试中很常见，难度系数相对来说也较大。通过此类题目可以训练学生思维的系统性和深刻性，使学生能够深入地思考问题，不为表面的各种干扰现象所迷惑，全面系统地思考题目所涉及的各个不同知识点。深刻的反面是肤浅，选择题的特点之一恰是在似是而非的多个答案中设计一个个“陷阱”，引诱学生肤浅作答。因而在平时的教学中若能恰当适量地选用此类选择题，就能够迅速地披露学生对所学知识理解的片面性和肤浅性，及时纠正学生的理解偏差及错误。

选择题题型小，训练机会多，见效快。只要长期坚持，那么想当然、凭直觉、盲目套用的错误习惯就可以逐步得到克服，从而提高解答选择题的准确率。

以上从几个方面探讨了在日常教学中通过加强选择题教学，来培养学生的思维品质，提高学生的综合解决问题的能力。选择题作为各种不同层次考试的主要题型，涉及到的知识面非常广。选择题本身特点就是从多个选项中选出正确答案，在日常教学中恰当地选用选择题，可以培养学生善于独立思考，有主见的评判事物的思维品质，不断提高其辨误能力。在日常的高等数学教学中，结合不同章节的具体教学内容，针对性地设计一些选择题，在学期的后期也可以结合考研题目的难度来设计一些综合性强的题目，提升学生对不同章节知识的综合运用和掌握。通过不断地加强和穿插进行选择题的训练，对培养和提高学生的思维品质有着积极的作用。