基于Matlab/Simulink的电液比例阀动态性能分析与仿真

邱兆玲

（青岛军民融合学院，山东 青岛 266400）

0 引言

电液比例阀由于电信号的变化不但能控制执行元件的运动方向，而且可对其作用力矩和运动速度进行无级调节，这些都是通过阀芯的移动实现的，同时，阀芯在移动过程中受到惯性力、液压力、库仑摩擦力、液动力及弹簧力等不同外力的影响，因此，需要分析作用在阀芯上各种力的性质和产生根源，以便消除或减弱其不利影响。

库仑摩擦力是影响电液比例阀性能的关键因素之一，不仅决定换向阻力，也影响阀的精确控制和响应特性，若阀芯静止不动，当需要改变其位置时，从静止开始动作，阀芯需要克服静摩擦，就会产生滞后，因而降低了响应速度和灵敏度。

1 电液比例阀概述

电液比例阀通过电-机械转换器来控制固体部件的运动或变形以达到实现流体控制的目的。图1为位移-力反馈型先导控制比例节流阀的原理结构图，本文以该阀为例说明电液比例阀的工作原理。

图1 位移-力反馈型先导控制比例节流阀结构原理图Fig.1 Structure schematic diagram of displacement-force feedback pilot control proportional throttle valve

滑阀式先导阀芯和插装式主阀阀芯之间的位置联系是通过反馈弹簧实现的。当比例电磁铁推动先导阀芯克服反馈弹簧下移y时，主阀阀芯上腔Vx的压力px下降，在压差（pA-px）的作用下，主阀阀芯上移使节流阀开启，主阀阀芯位移经反馈弹簧转化为反馈力Ksf（xf0+x）（Ksf为反馈弹簧刚度）作用于先导阀芯，最终和电磁力达到平衡[1]。通过改变比例电磁铁输入电流可以改变先导阀芯的位移y，从而改变主阀的开口大小，完成对液流的流量调节。并且利用位移-力负反馈在一定程度上可以抑制主阀阀芯上的摩擦力和液动力的干扰，图2为进口压力pA、出口压力pB给定时的信号流程框图[2]。

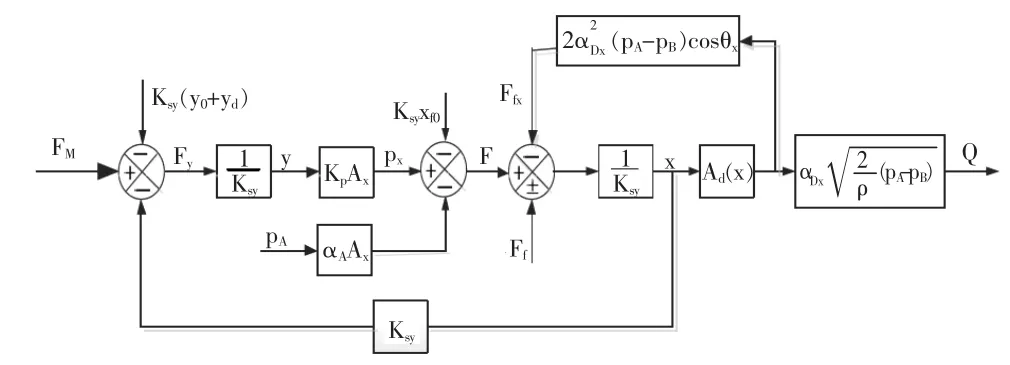
图2 位移-力反馈型先导控制比例节流阀的信号流程框图Fig.2 Signal-flow graph of displacement-force feedback pilot control proportional throttle valve

2 主阀阀芯的受力分析

液动力和摩擦力是电液比例阀阀芯的主要干扰量。液动力是阀口和阀腔内液流因动量变化而产生的反作用于阀芯的力即液体对固体施加的压力，主要有稳态液动力和瞬态液动力两部分；摩擦力分为牛顿摩擦力和库仑摩擦力两类，牛顿摩擦力是指流体的粘性阻尼力，而库仑摩擦力主要指干摩擦和边界摩擦。这里主要分析库仑摩擦力对阀芯运动的干扰作用。

阀芯对液流的控制功能是通过其位移实现的，因此，就必须对处于稳、暂态时的阀芯进行受力分析，找到合适的方法消除或减小摩擦力和液动力对阀芯运动的影响。

2.1 库仑摩擦力对主阀阀芯运动的干扰作用

当阀芯在阀腔内运动时，如果两者间隙中的油膜完整，则摩擦力表现为牛顿摩擦，但是，由于外力、变形、不同心等原因，总会存在或多或少的边界摩擦，因而在速度通过零点时有静摩擦与动摩擦的转换。

库仑定律认为库仑摩擦具有非线性特性，即静摩擦转换为动摩擦的不连续性、静摩擦力的最大值比动摩擦力要大以及动摩擦力与滑动速度无关。库仑摩擦力对速度的关系如图3所示[3]。图中粗实线及虚线为不同走向的库仑摩擦力，±Fmax为最大静摩擦力，±u为动摩擦的最低速度。

图3也同样反映了电液比例阀阀芯所受库仑摩擦力的非线性特性，它对阀芯运动的干扰作用表现为：一是当阀芯速度低于±u时，随着速度的降低，其动摩擦力逐渐增大，最终转化为静摩擦力，从而引起滞环；二是当阀芯速度高于±u时，动摩擦力并不随速度的变化而变化，而是保持不变即动摩擦力与速度无关，如果速度过高，则表现为动态特性的不稳定；三是当阀芯在换向瞬间的速度为零时，库仑摩擦力的大小和方向均有突变，引起阀芯零位时的流量死区。

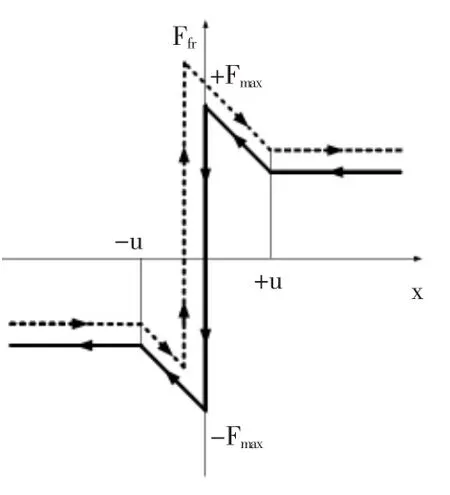
图3 库仑摩擦力与速度的关系Fig.3 Relation between coulomb friction and velocity

2.2 稳态时的主阀阀芯受力分析

由于几乎所有主阀都带有弹簧，因此，主阀阀芯运动是一个典型的质量-弹簧-阻尼系统的运动环节，如图4所示。

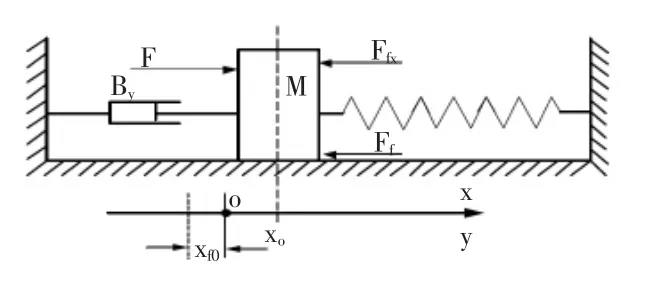
图4 质量-弹簧-阻尼系统Fig.4 M ass-spring-dam ping System

当主阀阀芯处于稳态即静止不动时，除了受到液压力、弹簧力的作用外，还有稳态液动力、静摩擦力等，根据图1可以得到主阀阀芯受到的液压力F，方向向上，其大小为：

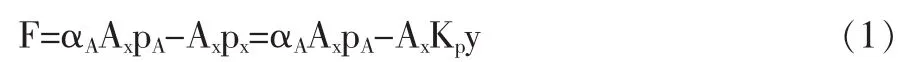
式中：y—稳态时先导阀阀芯的位移；pA—主阀下腔压力，设为定值；px—主阀上腔 Vx的压力（px=Kpy）；Kp—先导阀的压力增益，亦为定值；αA—主阀阀芯两端作用面积的比值；Ax—主阀阀芯上腔端面面积。

利用图4建立主阀阀芯的稳态力平衡方程，则

式中：x—由y引起的主阀阀芯的位移；xf0—反馈弹簧的预压缩量；Ffx—稳态液动力；Ff—静摩擦力。

将式（1）代入式（2）得到先导阀芯位移与主阀阀芯位移x的关系表达式：

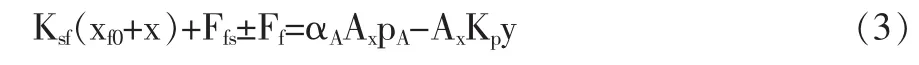
根据式（3）知，可以通过改变先导阀芯位移实现比例节流阀的流量控制。

2.3 暂态时的主阀阀芯受力分析

比例节流阀通过阀芯的位移来改变通流面积实现对流量的控制，从而完成对负载的速度调节，因而往往根据需要来调整阀芯的位移，使阀芯由一种稳态向另一种稳态过渡即阀芯要经历一个暂态的过程。

当需要改变流量时，只要改变式（3）y的值，阀芯就会失去平衡，其暂态过程的力表达式为[4]：

或

式中：M—阀芯及阀腔内油液质量；Bv—与粘性摩擦有关的阻尼系数；Bf—瞬态液动力阻尼系数；Ksfx—等效弹簧刚度；（Ksf为复位弹簧刚度，Kfx为液动力刚度或液动力位移增益）；—库仑摩擦力，由于位移-力负反馈的抑制，使得的影响较小，故予以忽略。

则式（5）的解为：

式中，Ae-ξω0、θ—暂态过程的振幅和初相角；ξ—阻尼比、ω0—无阻尼固有频率，与系统结构参数有关；ωd—阻尼固有频率，；右边第一项为暂态过程的衰减振动，随时间推移逐渐衰减直至消失；第二项是由引起的弹簧静变形[5，6]，为公式（5）的稳态解：

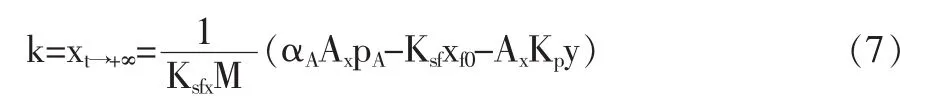
式（5）～式（7）反映了阀芯从暂态到稳态的过程，对式（7）变形、整理即可得到式（3），同时，由式（7）知，当 y 减小即先导阀芯下移时，主阀芯上腔Vx的压力px变小，主阀阀芯受到的液压力F增大，主阀阀芯向上移动的位移变大，相对应的弹簧静变形k（或x）变大，也就是弹簧的压缩量变大，其信号流程框图如图5所示。

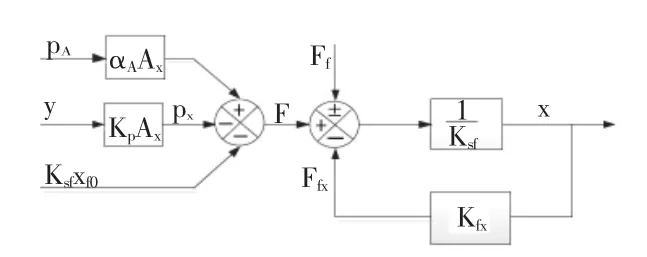
图5 主阀阀芯的信号流程框图Fig.5 Signal-flow graph of themain valve core

根据式（5），主阀阀芯移动时需要克服惯性力、瞬态液动力、粘性阻尼力、弹簧力等才能达到新的平衡，从而完成对流量的调节。

2.4 叠加颤振信号的主阀阀芯受力分析

从以上分析知，库仑摩擦力会使阀芯的静态特性具有滞环和流量死区，动态特性具有不稳定因素，同时，当阀芯长时间静止不动时，在液压径向不平衡力的作用下，容易导致边界摩擦，甚至干摩擦，造成阀芯液压卡紧无法动作[7]。这些因素对阀芯的干扰可以通过输入信号使其在平衡位置作微小振动消除或减小，而输入信号由控制信号加颤振信号组成[8]，即：

式中：y0—控制信号，输入信号y的平均值，为一定值；yd—颤振信号的振幅；ω—颤振信号的角频率。

将式（8）代入式（5）得到叠加颤振信号的主阀阀芯的力平衡方程：

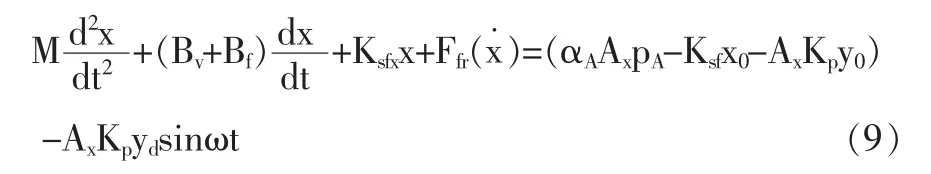
即只要颤振信号在半个周期内产生的附加作用力的算术平均值大于最大静摩擦力，主阀阀芯就不会出现静止状态，这时式（9）的解为：

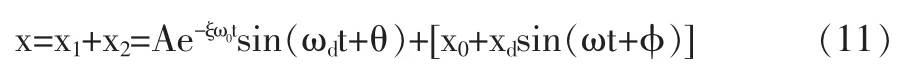
式中，x1为式（9）的通解或瞬态解，x1=Ae-ξω0tsin（ωdt+θ）对应于暂态过程的衰减振动；x2为式（9）特解或稳态解，当t→+∞时，

式中：φ—相角；x0—x2的平均值，由y0引起的静变形，与 y0成比例，由式（7）可得：

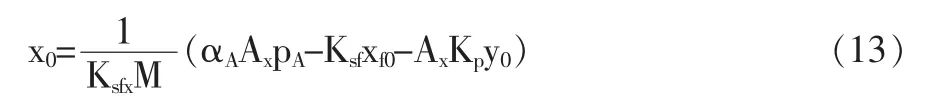
xd—主阀阀芯微小振动的振幅：

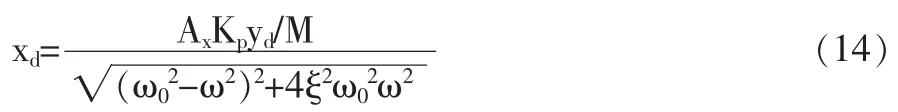
上式中，当颤振信号的频率ω→+∞时，振幅 xd→0，则式（9）的解即为式（13），因此，暂态过程可以看作是叠加颤振信号时的一个特例。

主阀阀芯的微小振动xdsin（ωt+φ）是由颤振信号ydsinωt引起的，其微小振动速度为：

由式（10）和式（16）知，提高颤振信号的振幅 yd或角频率ω，即可以满足力的要求，又可以满足速度的要求，但是过分提高yd或ω会增大磨损以及对被控元件引起振幅较大的脉动，并且对进一步减小动摩擦力并无作用，因此，叠加颤振信号时往往需要调节其频率和振幅。对于正弦颤振信号角频率ω大于固有频率为ω0的质量-弹簧-阻尼系统，由式（14）可知，颤振信号的频率过高会降低系统的幅值，所以颤振信号的频率一般采用系统自然频率二倍左右的固定频率，而振幅随控制信号的改变而改变，约为控制信号的10%～20%[3]。

3 动态性能分析及Simulink仿真

利用图5、式（5）和式（9）分别建立暂态和叠加颤振信号时的主阀阀芯系统动态结构图，如图6和图7所示。

建立一个可以模拟图6与图7所示系统对输入信号为阶跃函数和正弦函数时的系统输出响应情况的仿真系统，图8为其仿真系统图[9]。

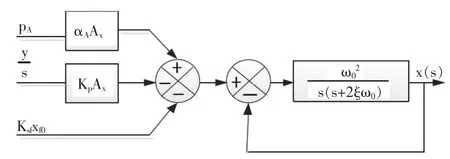
图6 暂态时的主阀阀芯系统结构图Fig.6 System structure diagram of transient state of themain valve core

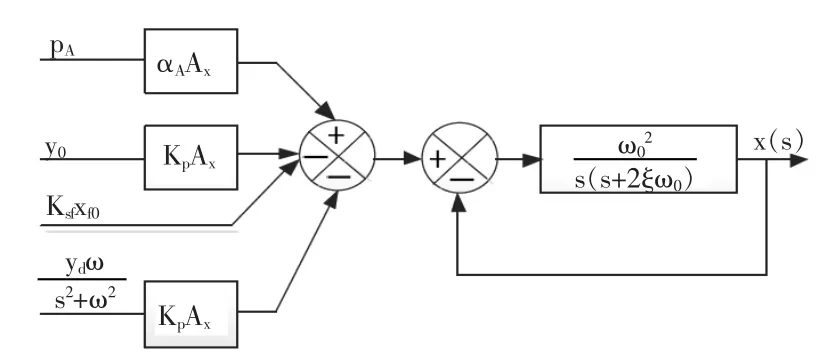
图7 叠加颤振信号的主阀阀芯系统结构图Fig.7 System structure diagram of themain valve core that superim posed dither signal

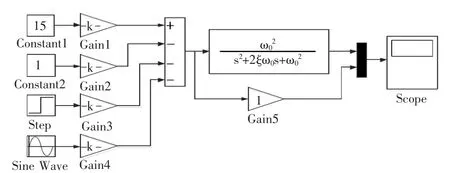
图8 系统仿真图Fig.8 System simulation diagram

某型号位移-力反馈型先导控制比例节流阀的部分工艺制造参数如表1所示。经实验测得，当进口压力pA=15MPa，出口压力 pB=10.5MP a，先导阀芯位移 y=0.3mm。在图8的系统仿真图中置αAAx，Gain3=Ksfxf0，Gain4=0 可得到先导阀芯位移 y=0.3mm时暂态过程的系统阶跃响应曲线，如图9所示。

表1 电液比例节流阀的部分参数Tab.1 PartialParam eters of Electro-hydraulicProportionalThrottle Valve

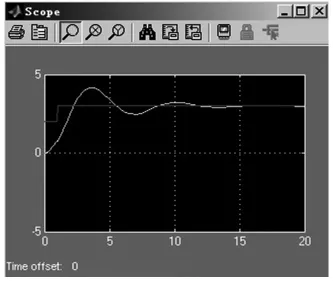
图9 系统阶跃响应曲线Fig.9 System step response curve

从图9所示的系统响应曲线看出，阀芯的振幅随时间的增大而逐渐减小，最终趋于平衡位置，符合公式（6）的曲线规律和由式（7）计算得到的弹簧静变形大小。

同理，在图8的系统仿真图中置Gain1=AxKp，Gain2=αAAx，Gain3=Ksfxf0，Gain4=AxKp可 得 到 y0=0.3mm，颤振信号振幅 yd=0.2×y0=0.06mm、频率 ω=50Hz的系统正弦波响应曲线，如图10所示。

图10 系统正弦波响应曲线Fig.10 System sinusoidal response curve

图10所示的正弦波响应曲线符合公式（11）的曲线规律，阀芯的振幅随时间t的增大而逐渐减小至颤振信号的幅值，其静变形大小与幅值大小分别与式（13）和式（14）计算得到的数值大小基本相符。

阶跃响应的仿真结果表明，当改变输入信号y的值时，系统能够克服惯性力、液动力、库仑摩擦力等力的影响重新达到新的平衡位置。但是若阀芯长时间停止不动，由于径向不平衡力、阀芯变形以及油液中的杂质进入阀芯配合间隙等原因增大了库仑摩擦力的影响，容易产生滞后，甚至造成液压卡紧现象，从而降低了阀芯的响应速度和灵敏度。

而正弦波响应的仿真结果显示，叠加颤振信号使阀芯在平衡位置作微小振动，这样就可以消除库仑摩擦引起的对阀芯的干扰，有利于改善控制系统的动态特性。

4 结束语

通过对电液比例阀在稳态、暂态及叠加颤振信号时的三种不同状态的受力分析和Matlab/Simulink仿真实验表明，在控制信号上叠加颤振信号，有利于消除液动力和库仑摩擦力对电液比例阀阀芯的干扰，无论是对稳态控制精度和动态响应性能，还是抗干扰能力或可靠性都有明显改善。因此，选择与电－机械转换器相匹配的控制放大器对电液控制系统的稳态和动态特性尤为重要。