立体车库服务系统存取车随机模型的研究
2018-12-13齐凤莲王永章张帼英刘冠诚
齐凤莲,王永章,张帼英,刘冠诚
(1.沈阳建筑大学,辽宁 沈阳 110168;2.北方重工防务事业部技术部,内蒙古 包头 014000)
0 引言
随着生活水平的提高,我国的汽车拥有量大幅度增加,据国家统计局数据显示,截止2015年底,每百户家庭拥有私家车31辆,汽车占机动车比例达到61.8%,汽车拥有量达到了16284.45万辆。汽车拥有量的大幅度增长,就需要大量的停车设施满足停车的需要。现有的停车设施大部分是平面停车场,不仅不能满足需要,而且大量占用土地面积,使城市土地资源越来越紧张[1~3]。立体车库的出现极大地缓解了停车位数量需求增加和停车位建设难之间的矛盾,但是立体车库在运行过程中也有很多不足的地方。现阶段,存取车耗费时间长是立体车库运行过程中的一个重要问题,针对这个问题,学者们在存取策略的优化问题上做了大量的研究[1~10]。笔者发现,学者们在对存取策略进行研究时,只是对一段时间或特定的存取队列进行优化分析,对于研究对象的描述与实际情况有较大出入,无法准确描述一天甚至更长时间段内的立体车库的运行情况,使得优化策略虽然获得了良好的优化效果,但只是特定情况下的情况,难以代表更为普遍的情况,所以需要为优化策略的研究提供一种更为贴近实际的模型。
本文从顾客的到达规律出发,创新性地引入了嵌入式马尔可夫链,建立了能够长时间模拟立体车库系统服务过程的动态模型,使存取策略的研究更加接近实际。而且该模型不依赖于特定的立体车库,所以也为研究各种立体车库服务过程中的情况提供了一个可行性。
1 立体车库服务系统概述
在立体车库系统中,顾客为了请求获得存车或取车服务而来到系统,若不能立即获得服务而系统又允许排队等待,则加入等待队伍,待获得服务后离开系统,这种服务模式符合排队论所研究的问题,所以立体车库是一个排队系统,或称随机服务系统。
对于排队问题,必须说明的问题有三个:①顾客到达系统的情况;②系统对每个顾客提供服务时所花费的时间长短;③系统对顾客提供服务的先后顺序。实际的排队系统各有不同,但概括起来都由3个基本部分组成:输入过程、服务机制、排队及排队规则[11]。
本文针对立体车库的实际运行情况,重点研究立体车库服务系统中的输入过程,以及输入过程和服务机制的结合。
2 基于非齐次泊松分布的输入过程
立体车库服务系统的输入过程描述的是顾客的来源以及顾客按照怎样的规律到达系统,前者说明的是顾客的总体数,后者说明的是顾客的到达类型和相继到达顾客的间隔时间服从什么样的概率分布[11]。
2.1 输入过程的研究现状
目前国内的学者们在研究过程中通常假设顾客的数量是无限的或不考虑顾客的数量,到达规律服从泊松流分布,以这种简化的到达规律对立体车库服务系统的服务对象进行研究,然后模拟一段时间内有若干个存取车顾客,以存取车比例来区分高峰和平峰[1~5],这种方法在普遍性和随机性上体现不明显,没有完全体现立体车库运行过程中顾客到达的随机性。
2.2 存取车规律汇总
对于立体车库的服务系统,顾客的到达规律是相当复杂的,与立体车库的建设位置和服务对象有密切的关联,如表1所示。为获得更准确的客流量数据,笔者在某商场做了为期一天的调查,部分数据如表2~表4所示。

表1 建设位置与顾客服务规律的关联Tab.1 The relationship between construction location and custom er service

表2 早晨时间段部分客流量情况Tab.2 Partial passenger flow in the morning time period

表3 中午时间段部分客流量情况Tab.3 Partial passenger flow at noon time

表4 傍晚时间段部分客流量情况Tab.4 Partial passenger flow in the evening time
调查数据显示,一天中顾客的到达强度是一个变化值,早晨存车较多但强度不是很大呈现平稳上升趋势,平时存取车平稳且存取车平衡。研究过程中发现,一种特定的顾客到达模型无法代表所有的立体车库服务场所和所有的时间段立体车库服务系统的顾客到达情况,即模型不具有代表性。为此本文结合顾客到达规律建立了一种具有广泛适用性的顾客到达模型。
2.3 基于非齐次泊松分布的顾客到达模型
对于立体车库的服务系统,我们对顾客的到达情况作如下假设:
(1)在不相交的时间区间中到达系统的顾客个数是独立的,即无后效性。
(2)在时刻 t,对充分小的时间长度 Δt,在时间区间[t,t+Δt)内有一个顾客到达的概率与t和Δt有关,与 t成函数关系 λ(t),约与 Δt成正比,即:

式中:P1—时间区间[t,t+Δt)内有 1 个顾客到达的概率;ο(Δt)—当 Δt→0 时,是Δt的高阶无穷小;λ—单位时间有一个顾客到达的概率,称为概率强度。
(3)对于充分小的 Δt,在时间区间[t,t+Δt)内有两个或两个以上顾客到达的概率极小,以致可以忽略,即:

式中:Pn—时间区间[t,t+Δt)内有 n 个顾客到达的概率。
假设1说明顾客的到达具有独立增量性,假设2说明顾客到达不具有平稳增量性,由假设我们得到顾客的到达规律是强度函数为λ(t)的非齐次泊松分布。令:

则:
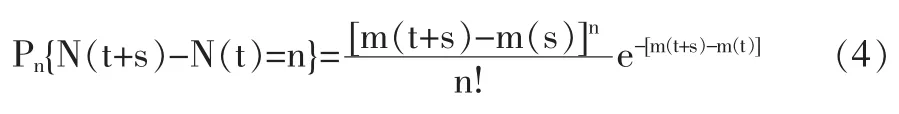
式中:Pn—时间长度为s内到达顾客为n时的概率;N(t)—时间区间[t,t+Δt)内到达系统的顾客数。
立体车库服务系统的顾客到达过程中,其强度函数λ(t)有界,在研究过程中将非齐次泊松过程看作齐次泊松过程的随机取样。即,λ(t)≤λ,在强度为λ的齐次泊松过程中,时刻t来到的顾客以概率λ(t)/λ被允许接受服务或加入等待队列,被接受的顾客所构成的分布就是符合强度函数λ(t)的非齐次泊松分布。
3 研究对象的动态模拟
3.1 服务机制
服务机制需要说明服务员的数量以及连接形式,顾客是单个还是成批接受服务,服务时间的分布情况,其中服务时间的分布情况是最重要的一项[11]。
立体车库服务系统中顾客是单个还是成批接受服务跟立体车库的结构有关,升降横移式可以多个顾客同时接受服务;垂直升降式顾客单个接受服务;巷道堆垛式的服务情况跟堆垛机数量有关。
立体车库的服务时间与其结构有关,升降横移式立体车库的服务时间同移动载车板的次数成正比,巷道堆垛式立体车库和垂直升降式立体车库的服务时间同服务车位的位置有关。目前学者对于服务时间的确定是通过建立立体车库服务时间的数学模型,用数学公式描述了服务时间与车位之间的关系[1,2,4,6,7,10]。
3.2 排队及排队规则
排队指的是队长的限制,对于立体车库一般是允许排队但不允许队长无限长。排队规则指的是排队等待的顾客接受服务的顺序是什么,一般有先到先服务、后到先服务、随机服务、有优先权的服务等[11]。
立体车库的服务系统,由于车位的数量有限,所以立体车库允许排队但不允许队长无限长。目前国内学者对于立体车库服务系统的研究侧重于排队规则。分析连续存车、连续取车、交叉存取和原地待命四种策略在不同时间段的应用,得出省时间的策略或策略组合[1~4]或采用遗传算法对一段时间的若干个存取车顾客的服务顺序进行优化[6~9]。
目前国内的学者在研究立体车库的存取策略时选择的研究对象一般是在一段时间内有若干个存取车顾客,然后将优化策略对这些顾客的服务时间进行计算,最后进行比较,得出一种优化策略[1~10]。
这种研究对象的选取方法只能模拟一段时间内的存取情况,无法说明实际情况中不同时刻有不同数量的存取车顾客排队等待时存取策略的优化情况。
本文创新性地引入了嵌入式马尔可夫链,使用马尔可夫链对顾客在接受服务过程中,系统中排队顾客的变化情况进行了模拟。应用此模型,多种优化算法可以在更接近实际情况的条件下进行模拟仿真,得到更有力的分析结果。
3.3 马尔可夫链定义
马尔可夫链的定义:设随机过程{X(t),t∈T}的状态空间为 I,如果对时间 t的任意数值 t1<t2<…<tn,n≥3,ti∈T 在条件 X(ti)=xi,xi∈I,i=1,2,…,n-1 下,X(tn)的条件分布函数恰等于在条件 X(tn-1)=xn-1下 X(tn)的条件分布函数,即:

则称随机过程{X(t),t∈T}为马尔可夫链。
马尔可夫链具有这样的性质,过程(或系统)在时刻t0之前所处的状态为已知条件下,过程在时刻t>t0所处状态的条件分布与过程在时刻t0之前所处的状态无关,即在已知过程“现在”的条件下,“将来”的状态不依赖于“过去”。
在立体车库服务系统中,顾客的到达规律符合泊松流,服务时间是确定但不是恒定的,若以X(t)记在时刻t系统中的顾客人数,在任意的时刻t,正在接受服务的顾客可能还没有服务结束,那么从时刻t起的剩余服务时间分布不再具有无记忆性质,即{X(t),t≥0}不具有马尔可夫性。
3.4 嵌入式马尔科夫排队模拟
为了解决这个问题,采用嵌入式马尔可夫链进行排队模拟,只在顾客离开系统时考察系统,即以Xn记第n个顾客离开系统后留在系统中的顾客数,n≥1。又以Yn记第n个顾客接受服务期间来到系统的顾客数,Tn记第n个顾客的服务时间。当Xn>0时,第n个顾客离开系统时剩余Xn个顾客,其中一个顾客接受服务,其余Xn-1个顾客排队等候。因此第n+1个顾客离开系统时系统将包含在排队的Xn-1个顾客以及第n+1个顾客服务期间来到系统的顾客。当Xn=0时类似。可得:

由于Yn,n≥1表示不相重叠的服务时间中来到系统的顾客数,到达规律服从泊松分布,所以相互独立,且:

当已知 Xn时,Xn+1只与到达过程有关,而与 X1,X2,…,Xn-1无关,所以过程{Xn,n≥1}是马尔可夫链,由于此马尔可夫链是界定在特定点上的,所以这个链又称为嵌入式马尔可夫链。
其一步转移概率是最重要的式子:

当 i≥1,时,

其中:M=m(t+Tn+1)-m(t),k=j-i+1
当 i=0,时,

其中:k=j
嵌入式马尔可夫链{Xn,n≥1}的一步转移概率矩阵可写成:

其中:

嵌入式马尔可夫链模型的建立需要的数据有顾客的到达规律和服务时间,到达规律在上一节已经说明,服务时间跟结构和服务类型有关。
3.5 模型应用
立体车库由于建设位置的不同,服务对象会有很大的差异,优化策略的研究也就不尽相同。本文建立的模型适合多种立体车库,而且由于是动态模拟,优化策略研究的结果更加符合实际情况。在使用模型过程中需要的参数有到达强度函数λ(t)和存取车比例函数p(t)。此模型假设在较长时间内顾客到达服从参数为λ(t)的泊松分布,在较短的时间段内顾客的到达强度可以认为是不变的,即服从齐次泊松分布,不同时间段内顾客的存取车比例不相同,通过调节存取车比例函数p(t)来适应不同时间段的情况。
4 结论
本文主要针对立体车库的服务系统进行了研究,重点对其客流的输入过程和排队服务等环节进行了深入研究,获得以下结论:
提出了一种新的与实际情况接近的存取车模型,即非齐次泊松分布规律,顾客到来强度是时间t的函数。
采用嵌入式马尔可夫链,提出了一种动态模拟排队的模型,该模型将顾客的到达规律和立体车库系统的服务时间结合起来,建立了一个立体车库的动态服务过程,更接近实际的研究对象。
本文提出的存取车模型和动态服务过程可以适用多种不同的排队规则,更好的服务多种类型立体车库和多种服务场合。
