五轴数控机床伺服跟随误差对S形试件法向轮廓误差影响

付 萌，刘前军，关立文，王立平

（1.清华大学机械工程系，北京 100084；2.中国机械工业联合会，北京 100823）

0 引言

五轴机床检测、优化与精度改进一直是机床研究热点[1，2]。切削试件检测能够真实反应五轴机床综合性能，成为机床最终验收和评价机床性能的重要手段。Ibaraki等设计由铣削加工平面构成的棱台试件，以特定加工模式实现五轴机床几何误差项解耦辨识[3，4]。张亚针对一种摇篮型五轴机床，根据误差敏感性设计加工试件，实现机床转动轴几何误差辨识[5]。

S形试件由中航工业成飞公司提出，用于五轴机床综合加工性能检验试件[6]，现已作为DIS草案将纳入国际标准ISO 10791 Part 7[7]。S形试件表面是非可展直纹面，存在扭曲角和原理误差，离散刀位插补造成加工误差[8]。Guan等研究圆柱侧铣加工S形试件曲面数控编程原理误差研究，给出了侧铣加工中测量原理误差补偿方法与加工数控编程刀位生成算法[7，9]。Sato等研究了数控编程与机床转动轴几何误差对S形试件的轮廓精度影响[10]。王伟等对比几种典型五轴加工试件速度与加速度特征，研究了S形试件动态检测优越性[11]。

高速铣削加工中伺服进给轴动态跟随误差是影响零件面型精度的主要因素，针对伺服控制系统改善机床加工轮廓精度的方法主要是提高伺服跟随性能与改善轴间性能匹配性[12]。Tsutsumi等研究双转台五轴机床平动轴与转动轴伺服匹配性对圆轨迹影响[13]。Ding等通过多体运动学与伺服进给系统建模仿真分析转台几何误差与转动轴伺服速度环参数对圆锥台试件加工影响[14]。Jiang等分析AB双摆头五轴机床伺服动态特性对S形试件与NAS979加工表面质量影响[15]。

本文根据圆柱侧铣包络原理，建立包络特征点在运动误差微分扰动下的影响关系，分析伺服跟随误差对S形试件加工影响。建立五轴机床进给伺服系统模型，搭建系统传递函数和仿真模型，分析不同参数及工况下伺服跟随误差。结合侧铣包络点关系，研究伺服参数对S形试件表面轮廓误差影响。

1 圆柱侧铣法向轮廓误差模型

基于圆柱侧铣包络成形原理[16～18]建立法向轮廓误差模型。对圆柱刀具侧铣包络特征线方程公式求微分，不考虑刀具半径误差得五轴机床刀具运动误差造成切触点在工件坐标系变化。

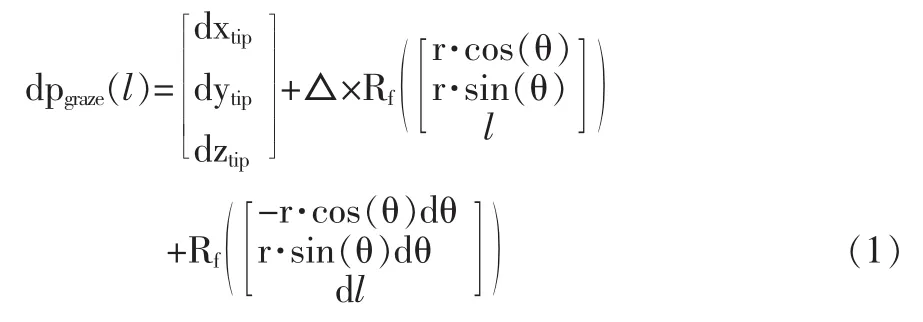
式中：△×—旋转矩阵姿态角微分变化的叉乘矩阵，表示旋转矩阵姿态角变化与旋转矩阵的关系：

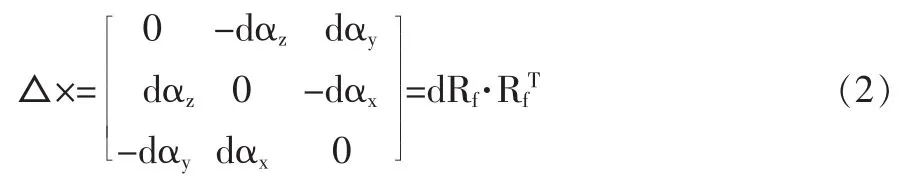
特征线切触点的位移变化在理论法向上的投影即曲面的法向轮廓误差如图1所示，可由dpgraze（l）与该点上的法向向量点乘计算。

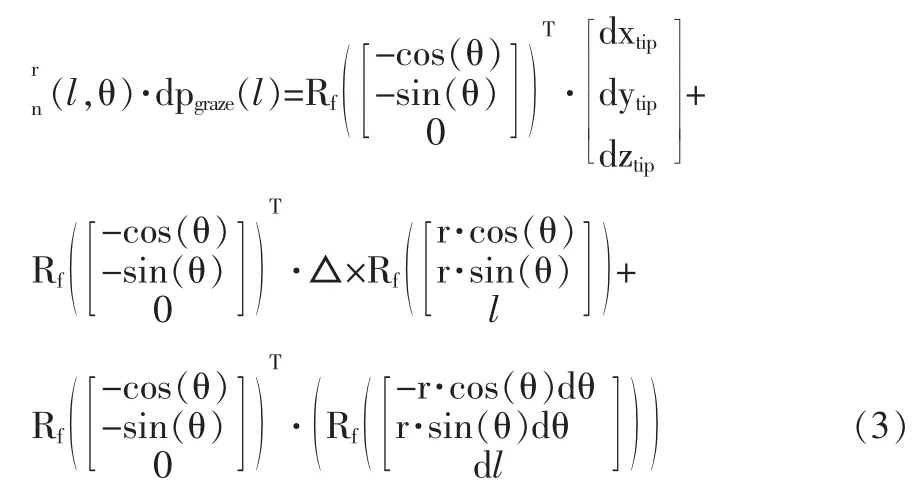
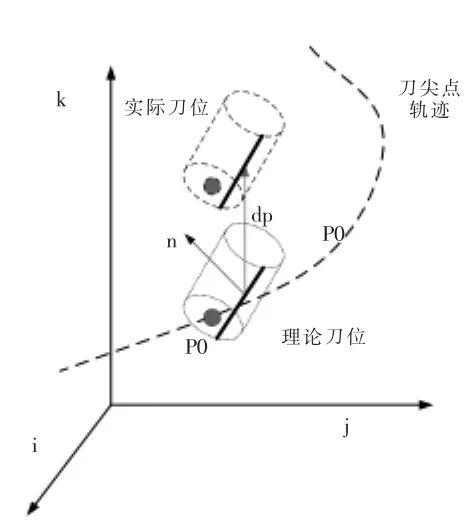
图1 包络特征点误差图Fig.1 Graze point error in flank m illing

由等式性质可知式（3）右边等式第三乘积项为0，其物理含义是由于瞬时速度引起的瞬时刀具坐标系沿圆周方向偏差dθ对加工面型法向误差没有影响。

根据上述分析法向误差可化简为：

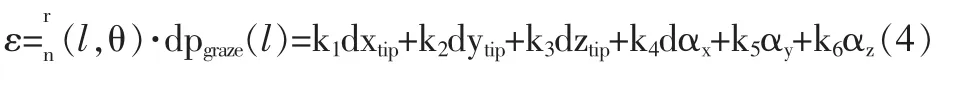
其中：dxtip、dytip、dztip、dαx、dαy、dαz分别 是刀具瞬 时 坐标Ff的系数k1～k6体现了刀具五轴运动误差对切削面型法向误差的影响。系数大小决定了相应刀具运动误差项对曲面相应点法向轮廓误差影响程度。

2 伺服跟随误差建模

确定五轴加工刀具轨迹与机床类型后，可由机床相关参数与机床运动学逆解方程求解加工过程中各个运动轴运动曲线。在非可展直纹面的加工中，不同刀位规划算法生成的理论刀具轨迹会存在差异[7]。选择常用的SPO算法，选取刀具直径20mm生成S形试件加工刀具轨迹，作为理论刀具轨迹。

选择一种AC双摆头的五轴机床为对象，根据机床多体运动学齐次坐标变换[1]，工件坐标系中刀轴方向矢量、刀尖点位置坐标与机床运动之间的关系如下式所示。

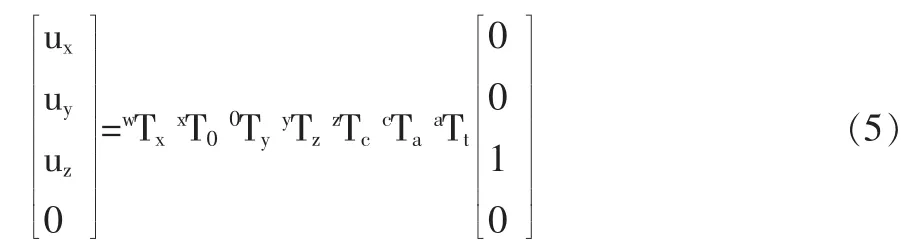
其中：（uxuyuz）T为刀具轴线在工件坐标系下方向矢量，aTt是t坐标系到a坐标的4×4齐次坐标变换矩阵。同理刀尖点位置坐标变换关系如下：

其中：（pxpypz）T为刀尖点在工件坐标系的位置矢量。

通过加工刀轨逆解可得加工S形试件时机床各驱动轴理论运动曲线，如图2所示，进给速度为1200mm/min，该曲线会随着对刀零点位置以及刀长变化而变化。

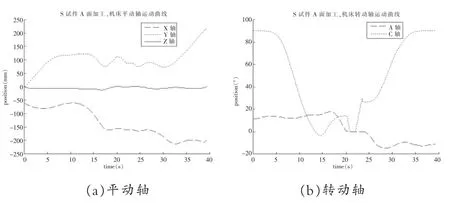
图2 S形试件A面加工伺服轴运动曲线Fig.2 Motion curve of servo axis of surface A of S shaped test piece machining

机床转动轴、直线进给机构等被控对象惯量、阻尼参数集中简化到电机输出端，忽略电流环影响，将电流环传递函数近似为1，则一般数控机床系统伺服系统模型如0所示。控制器采用速度环比例（P）控制器，速度环比例-积分（PI）控制器。Kpp位置环比例系数，Kvp速度环比例系数、Kvi速度环积分系数、Kf是电机转矩比例系数，J与B分别是控制对象的等效惯量和等效阻尼。对于机床转动轴图中R表示减速比，对于机床平动轴R则表示传动的螺距导程。

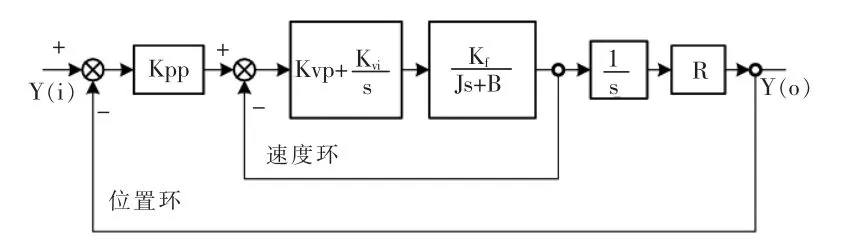
图3 伺服系统框图Fig.3 Servo control loop ofmotion axis

根据简化伺服系统图，可得伺服驱动轴位置指令输入与输出闭环传递函数如下：

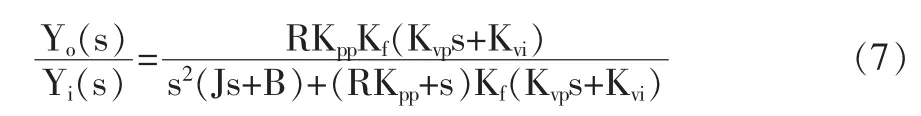
根据传递函数与伺服系统模型在Matlab Simulink中搭建仿真模型，机床各驱动轴参数见表1，将伺服轴指令运动曲线作为模型输入，得到各个驱动轴动态跟踪曲线，见图4。

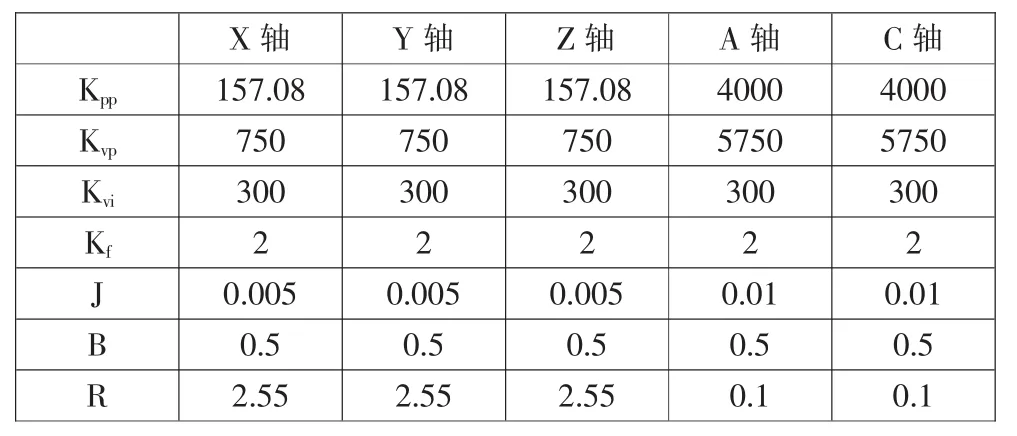
表1 机床伺服轴参数Tab.1 Servo dynamics and controller parameters

图4 S形试件A面加工伺服轴跟随误差曲线Fig.4 Tracking error of servo axis of surface A

由图4可知各轴存在较为明显的跟随误差，且随运动速度及加速度变化而变化。在后端负载系统确定后，可以通过控制器Kpp、Kvp与Kvi参数优化改善伺服轴动态跟随性能，提高伺服轴的轨迹跟踪性能进而提高机床加工精度。

3 侧铣轮廓法向误差仿真

将各轴跟随误差忽略瞬时速度矢量方向的变化，代入多体运动学方程得到刀具瞬时误差，将其代入包络特征点法向轮廓误差计算公式，得到跟随误差引起的S形试件加工法向轮廓误差如图5所示。

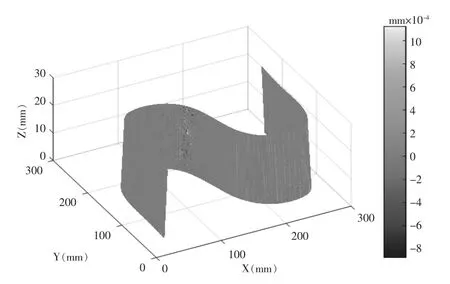
图5 S形试件A面曲面误差Fig.5 Profile error of surface A

对比伺服轴跟随误差和S形试件曲面法向轮廓可知：当各轴存在较大伺服跟随误差但五轴伺服跟随性能匹配时，曲面可以达到较好轮廓精度。所以在五轴机床伺服参数优化时，在满足一定伺服刚性条件下提高五轴伺服匹配性可有效降低曲面轮廓误差，不必过分追求伺服跟随误差最小。

提高两个转动轴位置环比例系数Kpp到8000，仿真计算转动轴跟随误差如图6所示 ，可知位置环比例系数增大，A轴与C轴两个转动轴跟随误差显著减小。

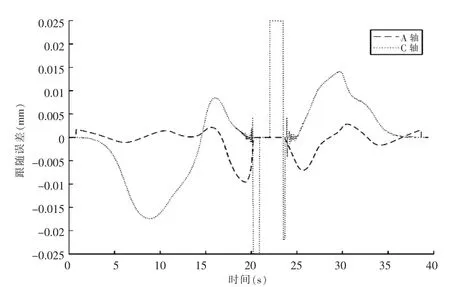
图6 转动轴伺服跟随误差曲线Fig.6 Tracking error of rotary axis （Kpp=8000）

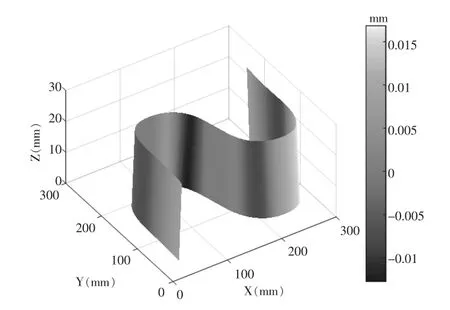
图7 新伺服参数的S形试件曲面误差图Fig.7 Profile error of the S test piece （Kpp=8000）

进一步计算S形试件表面法向轮廓误差如图7所示，在S形试件加工表面上出现明显误差，最大0.015mm欠切及0.01mm过切。转动轴伺服参数调整提高了转动轴伺服跟随性能，但改变了转动轴与平动轴间伺服匹配关系，导致曲面法向轮廓误差增大。

4 结论

在圆柱铣刀侧铣包络特征线求解模型基础上，建立了刀具误差与包络特征点法向轮廓误差的微分关系。以AC双摆头机床为例，建立了五轴机床简化的伺服进给系统，分析了加工S形试件时各轴跟随性能。应用轮廓误差微分关系，研究了伺服跟随误差对S形试件表面轮廓误差影响。通过改变转动轴伺服参数，分析了伺服匹配性对试件轮廓误差影响，可知S形试件对五轴机床高速加工检测时检验五轴伺服匹配性的优越性。