柔性轮轨下轮轨波磨综合作用的振动特性研究

宋志坤， 侯银庆， 胡晓依， 张浩然, 李 强, 成 棣

(1. 北京交通大学 机械与电子控制工程学院，北京 100044; 2. 中国铁道科学研究院 高速轮轨关系实验室， 北京 100081)

钢轨波磨是在轨面沿纵向一定长度范围内出现的周期性不平顺[1]；车轮谐波磨耗是车轮踏面周向出现的周期性不平顺。2种磨耗在客货混运铁路、地铁及高速铁路中均普遍存在。高速铁路存在的钢轨波磨的波长一般为短波长，引起的振动频率一般为300～600 Hz左右，而高阶的车轮谐波磨耗引起的振动频率一般为500 Hz[1]。针对轮轨磨耗引起的高频振动，国内外学者做了大量的研究。Nielsen[2]针对车轮失圆状态建立了数学模型和计算机程序用于模拟轮轨接触力和车辆/轨道响应的影响；Johansson[3]通过数值仿真和现场试验相结合的方法分析了非圆化车轮对轮轨垂向力的影响；Knothe[4]介绍了轨道模型的建立，并利用频响函数分析轨道的高频振动特性；吴海涛[5]利用UM建立了柔性轨道的车辆耦合动力学模型，分析了地铁线路钢轨波磨引起的高频动态特性；西南交通大学金学松[6-9]团队通过现场试验与仿真结合的手段研究车轮多边形对轮轨力及构架振动的影响。尹振坤[10]基于转向架部件损坏建立了车辆耦合动力学模型，分析车轮多边形磨耗对轮轨力的振动响应；刘韦[11]、宋志坤[12]通过有限元建立了柔性轮对的车辆耦合动力学模型，分析了谐波磨耗对轮轨作用力的影响。但目前的研究基本停留在对钢轨波磨和车轮谐波磨耗的单独研究，尚缺乏综合考虑轮轨均存在谐波磨耗时的振动特性，且仿真模型也只单独考虑了柔性轮对或柔性轨道，没有考虑到轮轨均为柔性状态下的振动响应，致使仿真结果与实际情况存在一定的差距。

本文以某型高速动车组为研究对象，通过ANSYS有限元软件和SIMPACK动力学软件建立了基于Timoshenko梁的柔性轨道和柔性轮对的车辆-轨道耦合动力学模型。通过对实验数据的统计与分析，选取了3种典型的车轮谐波磨耗(20阶，幅值0.01～0.03 mm)，16种钢轨波磨(波长120～150 mm，幅值0.01～0.04 mm)进行综合分析，研究了轮轨谐波磨耗在不同速度、波长及幅值下的动力学响应。

1 轮轨谐波磨耗的数值模型

1.1 车轮谐波磨耗

通过对某型车轮谐波磨耗进行跟踪测试，得到镟后13.1万km实测结果,见图1(a)。由图1(a)可知，左右轮均出现了明显的谐波磨耗。通过MATLAB编程软件对实测数据进行傅里叶变换处理，得到阶次幅值，见图1(b)。分析可知，在20阶时左轮和右轮的粗糙度幅值明显增大，可确定轮对是由20阶主导的谐波磨耗。仿真计算时，将20阶主导的谐波磨耗处理成理想化的简谐波，左右轮谐波磨耗的初始相位角均为0，不考虑相位差。

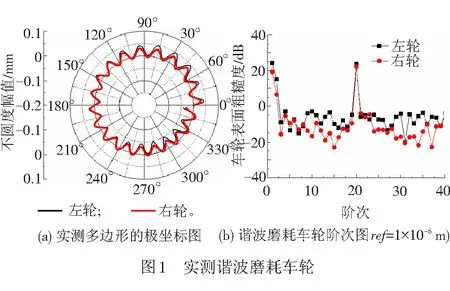
1.2 钢轨波磨的数值模型

钢轨波磨表现为轨道纵向的不平顺，呈多处非连续性的沿钢轨纵向分布在轮轨接触表面，在高速铁路的高速区主要以短波形式存在，波长一般为120～150 mm，幅值为0.04 mm左右[1]。实际测得的钢轨波磨一般以不规则的波长及幅值分布在钢轨表面，但仿真计算中通常将其处理成周期性的正弦波，表达式为

(1)

式中:zrw为钢轨表面波磨的垂向位置；dp为幅值；λ为波长；xrw为钢轨的纵向距离；φ为简谐波的初始相位角。假设钢轨波磨的波长为150 mm，幅值为0.04 mm，初始相位角均为0，不考虑左右轨谐波磨耗的相位差，将实测京沪线路不平顺与波磨进行叠加，见图2。这样不仅考虑了轨道激励，还考虑了钢轨轨面的波磨。

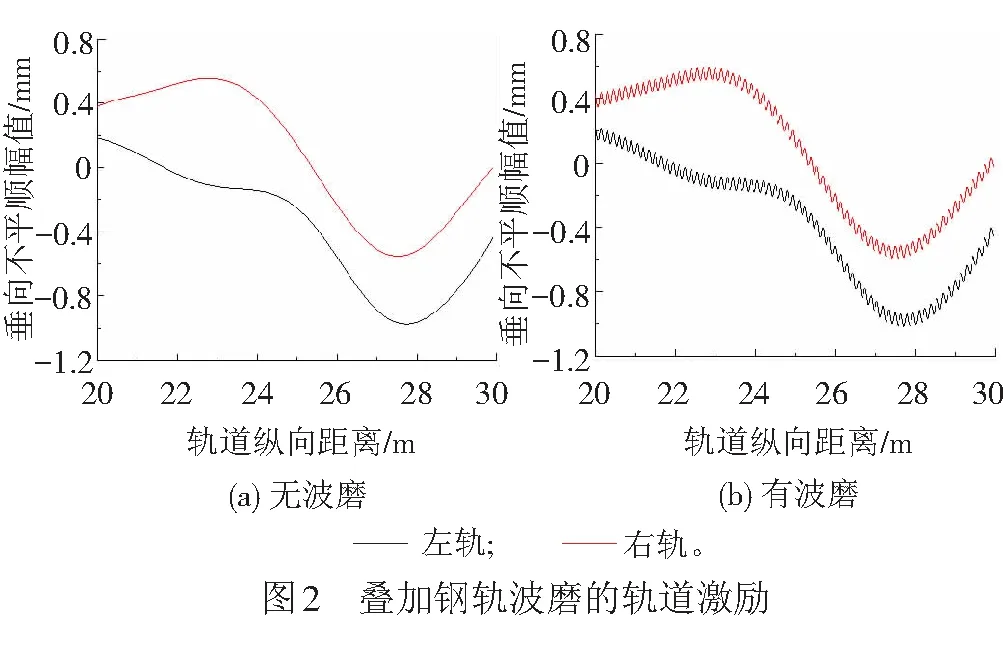
2 车辆轨道系统动力学模型

2.1 轮对柔性化

考虑轮对柔性化的主要目的在于研究轮对高阶模态如何影响轮轨高频振动行为。本文利用ANSYS建立轮对的有限元模型(见图3)，其中轮对的弹性模量为2.1×105MPa，泊松比为0.3，密度为7.85×103kg/m3。选取648个主自由度点进行子结构分析，将分析后的柔性轮对导入SIMPACK中，运用 SIMPACK中自定义参考点法，将轴箱连接处的主自由度点与车轴空心处的Marker点进行刚性铰接，以替代刚性轮对。通过查看缩减模态，发现柔性轮对高频垂向共振频率仅存在2种情况，即19阶的605.2 Hz和21阶的681.23 Hz。

2.2 轨道柔性化

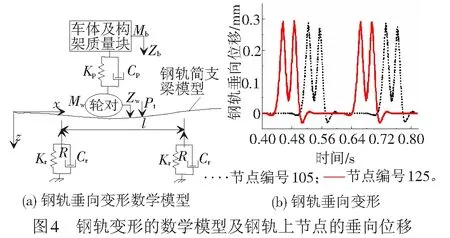
首先利用ANSYS建立单根长度为126 m的60D钢轨的有限元模型，并进行子结构分析。再利用MATLAB编写柔性轨道的配置文件(包括:轨道模型、空间放置位置、轨枕间距)等信息，通过SIMPACK中的FLEXTRACK模块读取配置文件，从而实现轨道的柔性化。轨道端部利用力元进行固定，横向、垂向与纵向3个方向的刚度为1×104MN/m，阻尼为1×104(kN·s)/m。轨枕、道床等轨下部分统一采用弹簧阻尼元件模拟，其中部分轨道参数设置见表1。柔性轨道可视为上部受轮轨垂直力，下部受等间隔分布的轨枕支反力的简支梁。取四分之一的整车模型考虑，其运动受力见图4(a)。其中，Mw为轮对质量；Mb为一系簧上质量；Zb为一系簧上质量块的垂向位移；l为轨枕间距；Zw为轮对的垂向位移；R为轨下约束的支撑反力；Cp，Kp为一系阻尼与刚度；Cr，Kr为轨下阻尼与刚度。设车速度为300 km/h时，考虑轨道激励下的钢轨垂向变形见图4(b)。

表1 轨道计算参数

2.3 模型对比分析

为了探究柔性轮轨下轮轨谐波磨耗综合作用时的振动特性，将车体与构架考虑为多刚体，建立了包括刚性轮轨、柔性轮刚性轨、柔性轨刚性轮、柔性轮轨共4种模型进行对比分析，多刚体动力学模型验证见文献[13]。其中柔性轮轨的整车模型见图5。仿真计算时将1号车轴左右轮设为谐波磨耗车轮，其余轮对为正常轮。钢轨波磨与实测不平顺叠加后的轨道激励以5 mm间隔加在纵向距离的30～60 m处。统一取右轮与右轨的仿真结果进行分析。

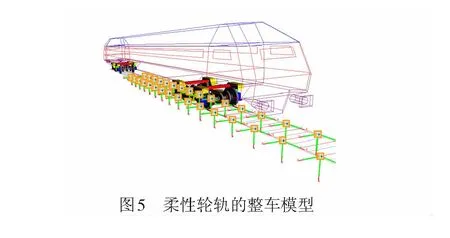
设车速为300 km/h，钢轨波磨波长为140 mm，幅值为0.04 mm；车轮谐波磨耗为20阶，幅值为0.01 mm。计算了4种模型在实测京沪轨道不平顺下轮对谐波磨耗、钢轨波磨、轮轨波磨3种工况下的轮轨垂向力，见表2。其中柔性轮轨下不同工况的轮轨垂向力频谱见图6。

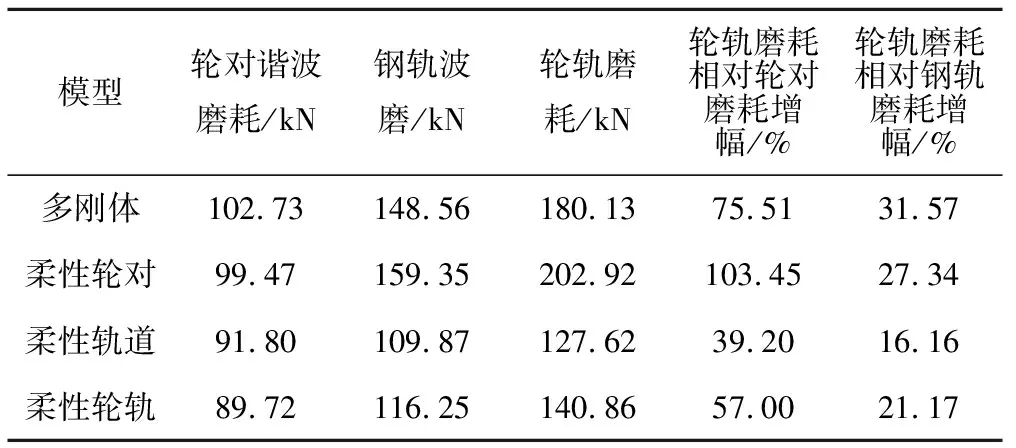
表2 不同模型、磨耗在轨道激励下的最大轮轨垂向力

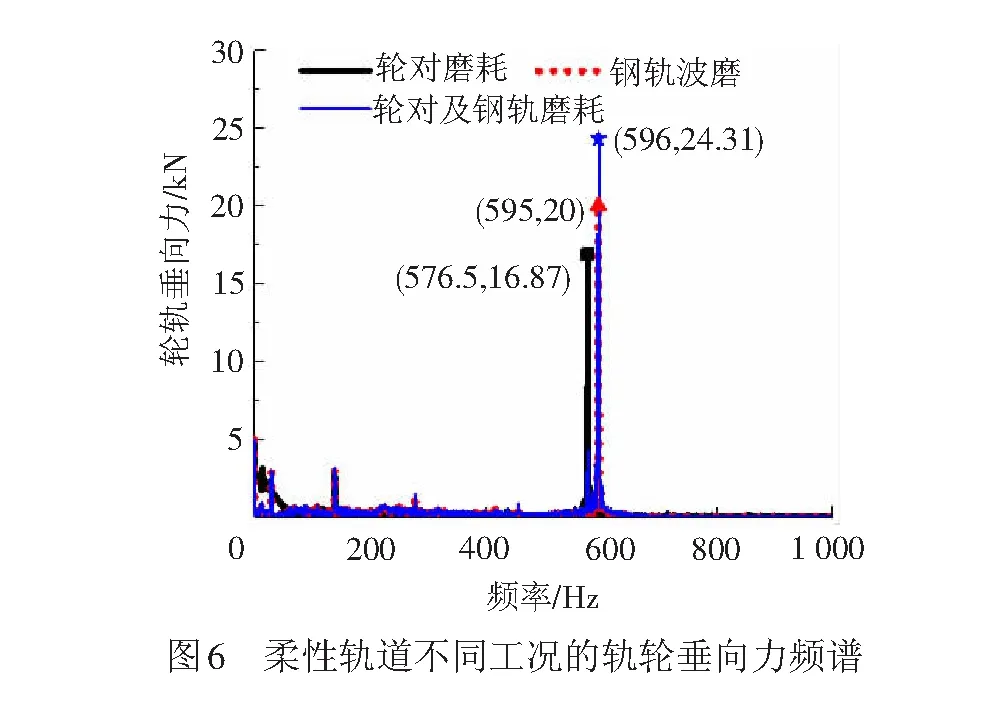
由表2、图6可见，单独考虑轮对的谐波磨耗或钢轨波磨时与两者综合考虑时的轮轨垂向力存在明显的差异，且不同模型得出的仿真数据也存在较大的差距。同为柔性轨或者刚性轨时，速度为300 km/h下20阶车轮谐波磨耗引起的振动频率为576.5 Hz，远离柔性轮对的垂向共振频率，此时刚性轮产生的轮轨力大于柔性轮；仅由140 mm波长的钢轨波磨引起的振动频率为595 Hz，激发了轮对的19阶模态共振，导致柔性轮产生的轮轨力大于刚性轮。轮对状态相同时，柔性轨下的轮轨垂向力小于刚性轨，因为该速度下无论是钢轨波磨还是轮对谐波磨耗产生振动频率均不在钢轨垂向共振频率范围内，钢轨固有频率见文献[14-16]。

3 柔性轮轨下轮-轨磨耗的影响分析

为了研究柔性轮轨下轮轨非均匀磨耗综合作用引起的振动特性，取20阶车轮谐波磨耗，幅值为0.01～0.03 mm；钢轨波磨的波长为120～150 mm，幅值为0.01～0.04 mm，研究轮轨非均匀磨耗在不同速度、波长及幅值下的振动特性。

3.1 轮轨谐波磨耗对轮轨作用力的影响

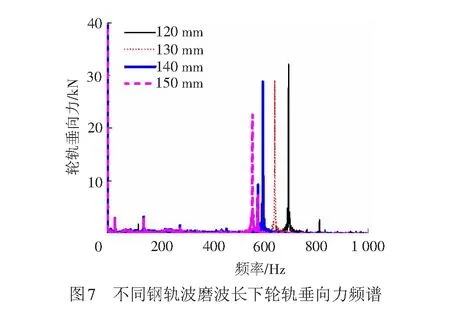
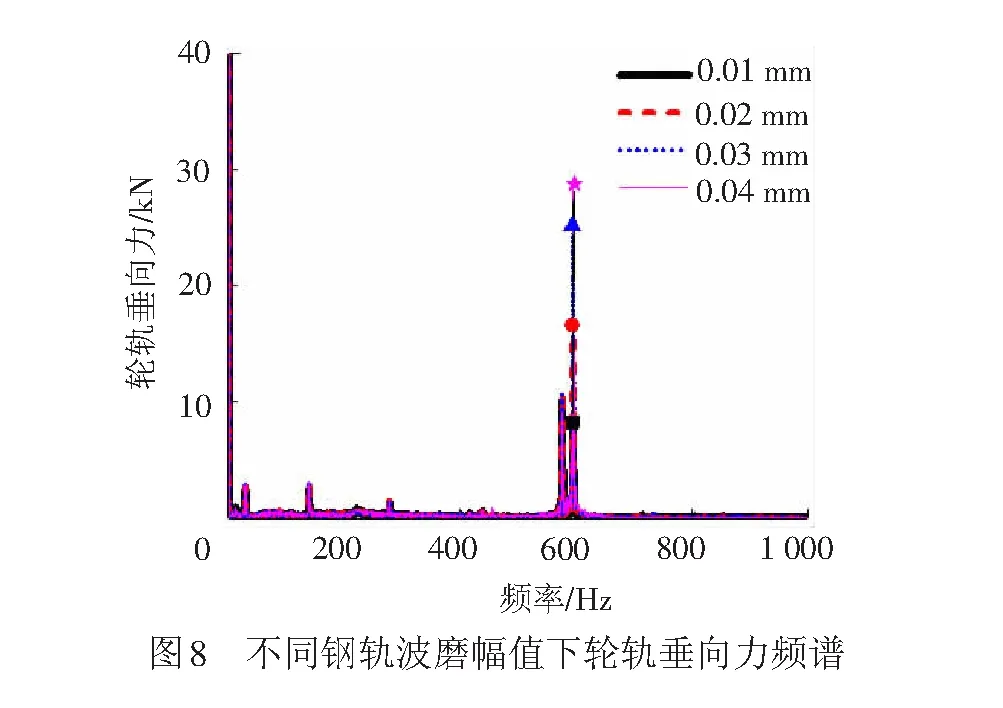
设车速为300 km/h，车轮谐波磨耗幅值为0.02 mm，阶次为20阶，其钢轨波磨幅值为0.04 mm，不同波长产生的轮轨垂向力及脱轨系数见表3；钢轨波磨波长为140 mm，不同幅值产生的轮轨垂向力及脱轨系数见表4。分别作轮轨垂向力频谱图，见图7、图8。由表3、图7可知，轮轨垂向力基本随着钢轨波磨波长的增加而减小，且轮轨磨耗综合作用下存在2个幅值较大的高频振动分量，分别由车轮谐波磨耗和钢轨波磨引起，钢轨波磨引起的轮轨垂向力幅值大于轮对谐波磨耗，是因为钢轨波磨的幅值大于轮对谐波磨耗的幅值。同时可以看出，波长分别为140，130 mm时产生的轮轨垂向力相差不大，主要是由于波长为140 mm时钢轨波磨引起的振动频率为595 Hz，激发了柔性轮对的19阶垂向共振。由表4、图8可知，轮轨垂向力随着钢轨波磨幅值的增大而增大。

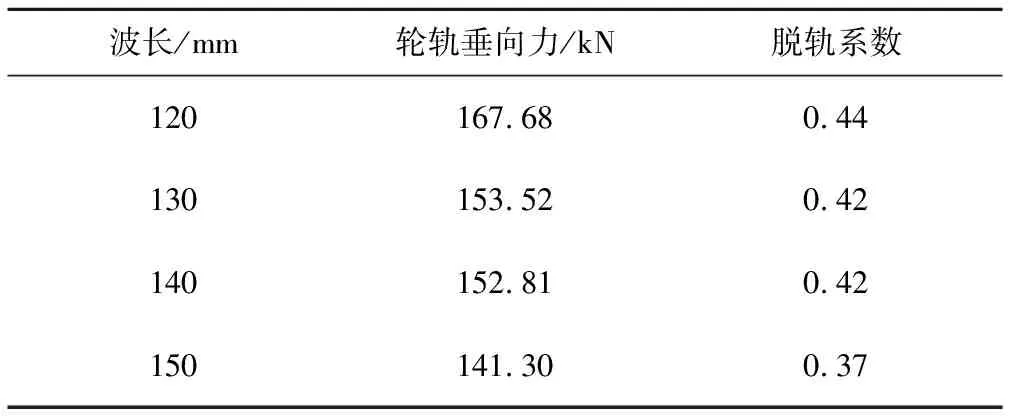
表3 波长120～150 mm下轮轨垂向力最大值及脱轨系数

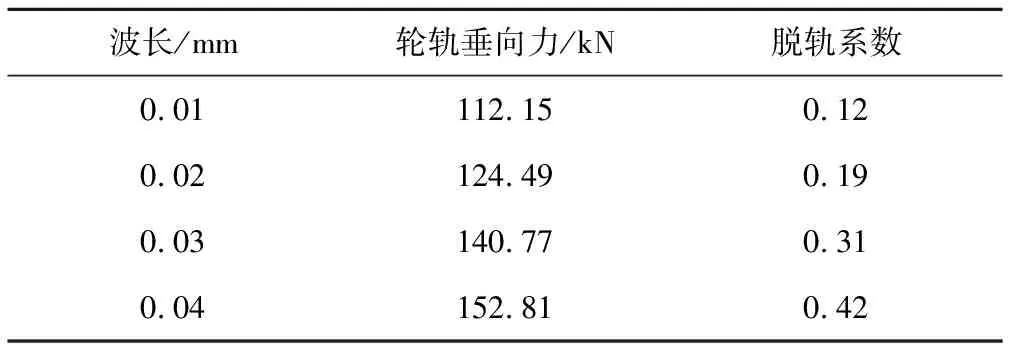
表4 幅值0.01～0.04 mm下轮轨垂向力最大值及脱轨系数

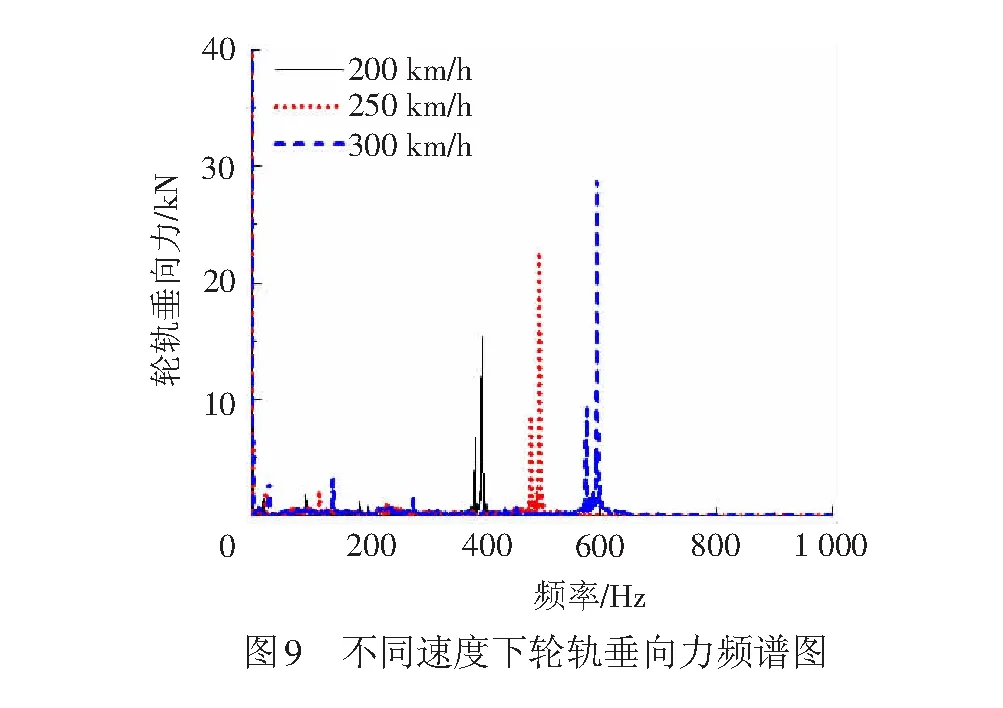
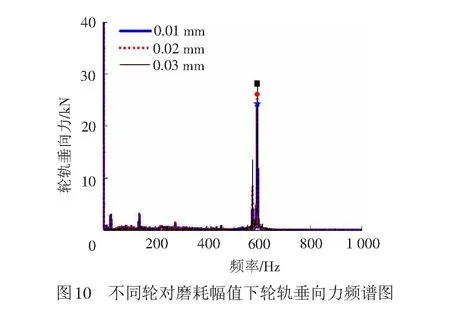
取钢轨波磨波长、幅值分别为140、0.04 mm，车轮谐波磨耗幅值为0.02 mm，阶次为20阶，其不同速度、幅值下产生的轮轨垂向力最大值及脱轨系数垂向力见表5、表6、图9。由图9可知，轮轨垂向力基本随着速度的增加而增加，车速度为300 km/h时轮轨垂向力增幅较大，这是因为该速度下引起的振动频率为595 Hz，激发了轮对的19阶模态共振。由图10可知，轮轨垂向力随着轮对谐波磨耗幅值的增大而增大。

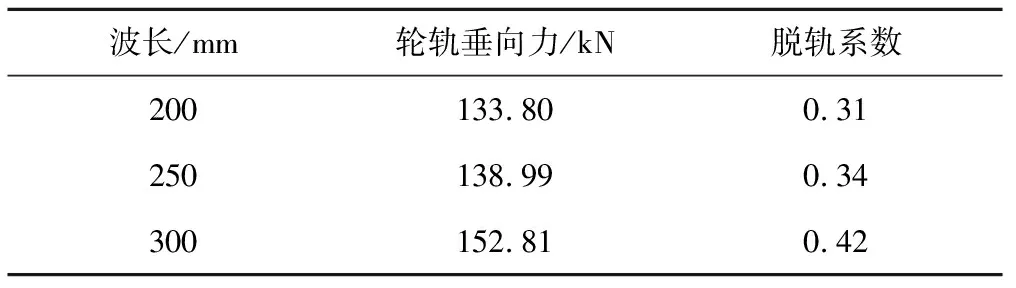
表5 车速度为200～300 km/h时轮轨垂向力最大值及脱轨系数

表6 幅值0.01～0.03 mm时轮轨垂向力最大值及脱轨系数

3.2 轮轨谐波磨耗对钢轨振动加速度的影响

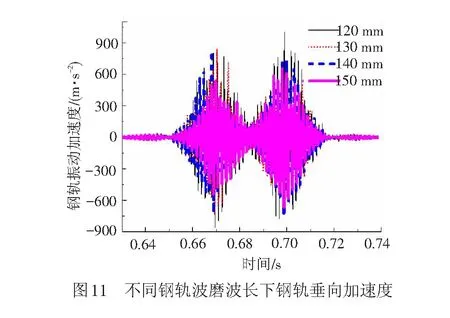
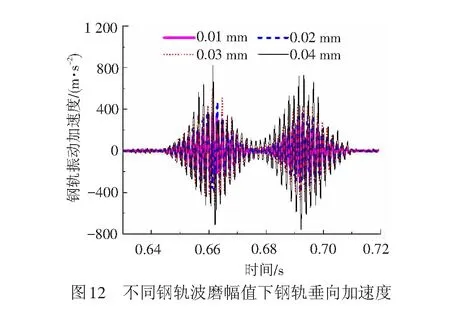
设车速度为300 km/h，车轮谐波磨耗幅值为0.02 mm，阶次为20阶，钢轨波磨幅值为0.04 mm，不同波长、幅值下钢轨振动加速度的时程曲线见图11。由图11可知，随着波长的增加，钢轨振动加速度基本呈减小趋势。波长为130、140 mm时引起的振动加速度相差不大，其原因是波长为140 mm时引起的轮对共振加剧了钢轨振动。由图12可知，钢轨振动加速度最大值随着幅值的增加而增加。

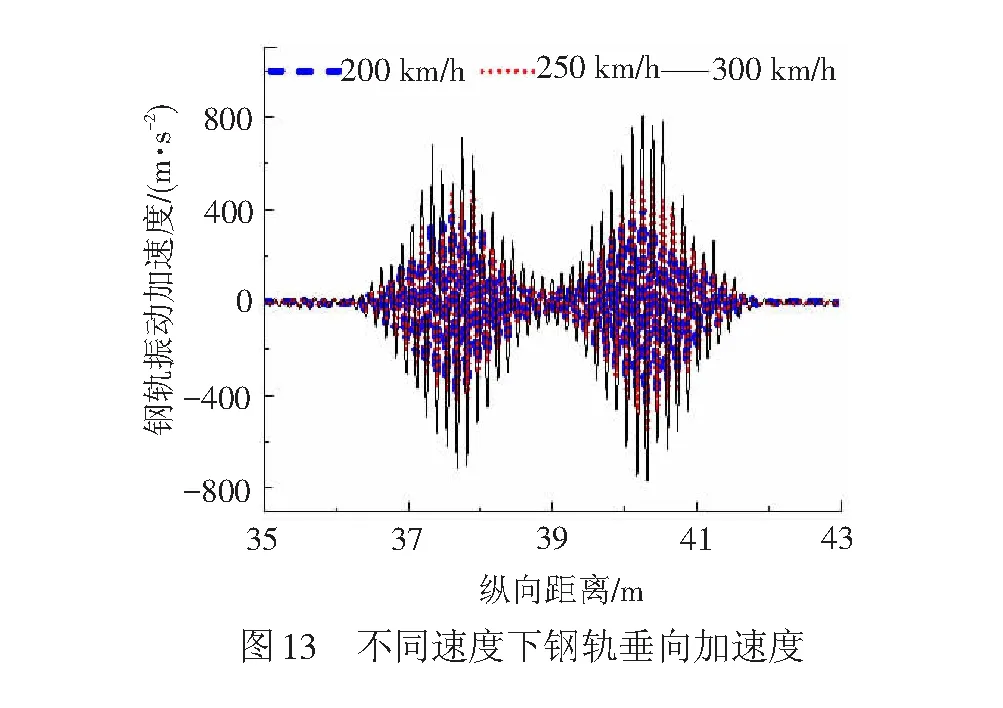
取车轮谐波磨耗幅值为0.02 mm，阶次为20阶，钢轨波磨的波长、幅值为140，0.04 mm，做不同速度、幅值下钢轨振动加速度时程曲线，见图13。由图13可知，车速度为300 km/h时振动加速度幅值明显变大，主要是由于该速度下激发了轮对共振，加剧了钢轨的垂向振动。由图14可知，钢轨振动加速度随着轮对磨耗幅值的增加而增加。

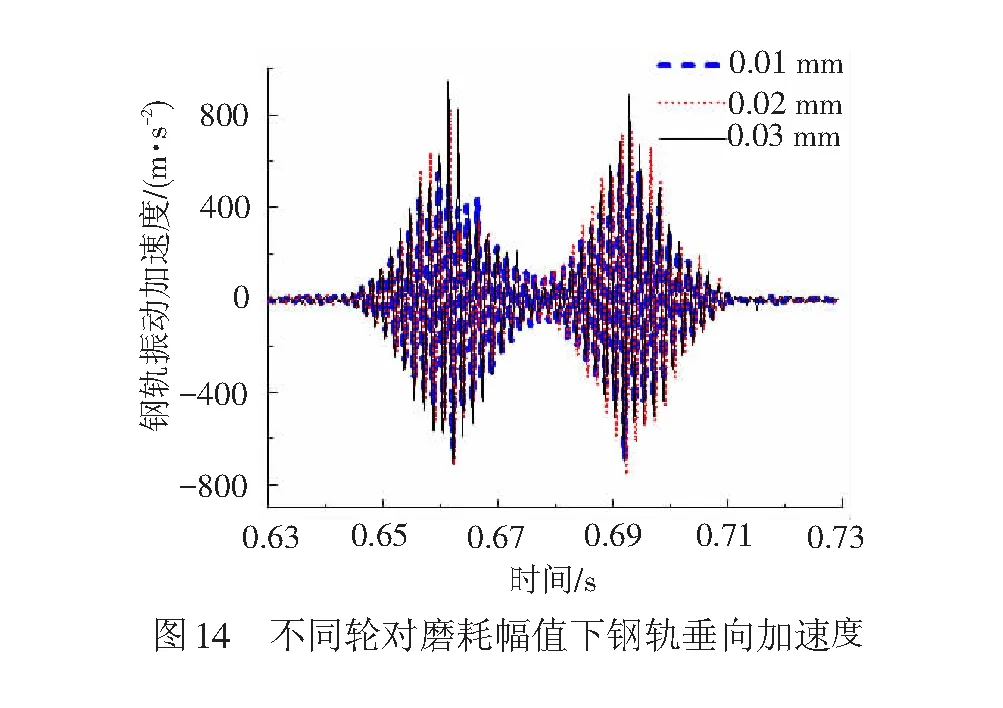
3.3 轮轨谐波磨耗对轮对振动加速度的影响

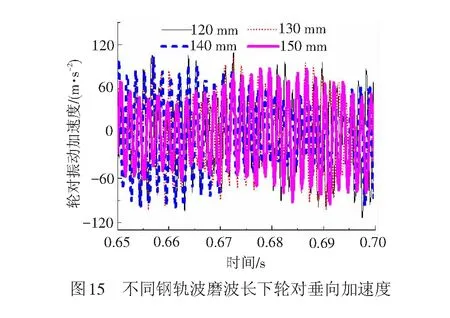
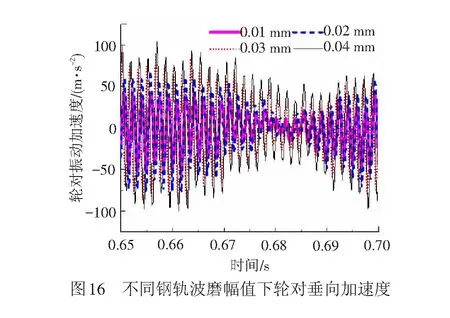
设车速度为300 km/h，车轮谐波磨耗幅值为0.02 mm，阶次为20阶，钢轨波磨幅值为0.04 mm，其不同波长、幅值下轮对振动加速度的时程曲线见图15。由图15可知，随着波长增加，轮对振动加速度基本呈减小趋势。波长为130、140 mm时轮对振动加速度偏差较小，其原因是波长为140 mm时产生的振动频率激发了轮对的19阶模态共振。由图16可知，随着幅值的增加轮对振动加速度逐渐增大。

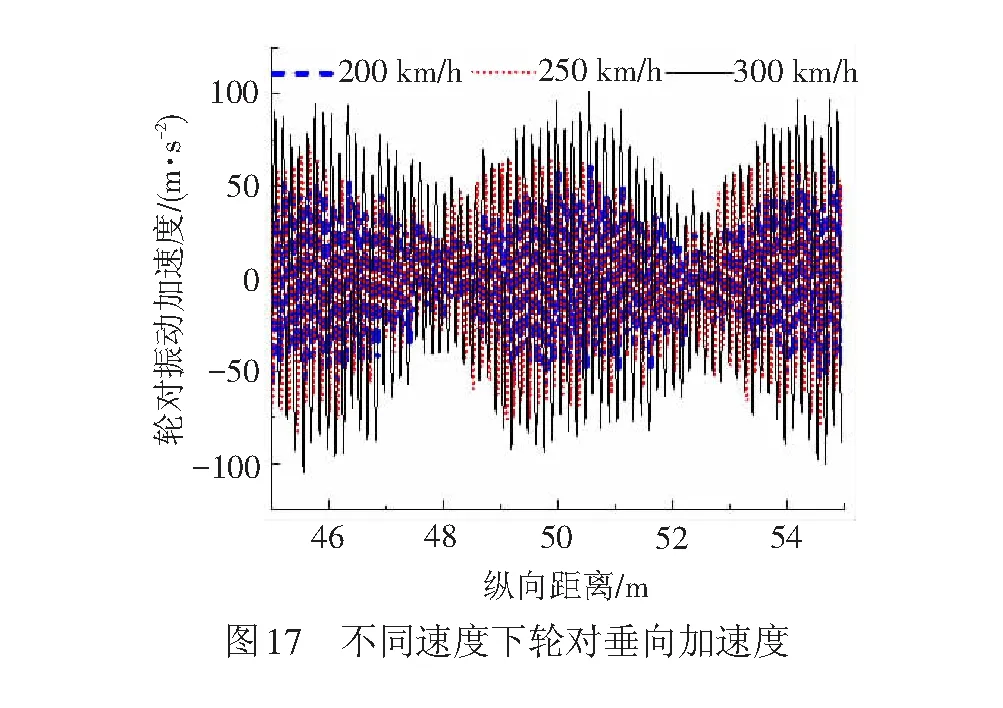
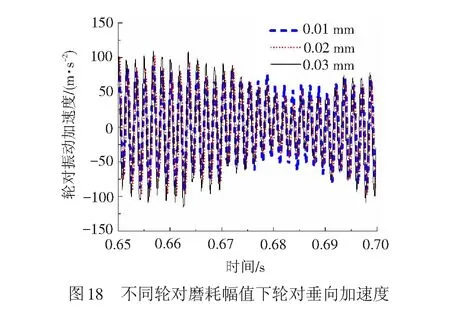
取钢轨波磨波长、幅值分别为140 mm、0.04 mm，车轮谐波磨耗幅值为0.02 mm，阶次为20阶，其不同速度、轮对磨耗幅值下的轮对振动加速度曲线见图17。由图17可见，轮对振动加速度基本随着速度的增加而增加。取同等钢轨磨耗，车速度为300 km/h时，不同幅值下20阶谐波磨耗引起的轮对振动加速度见图18。由图18可知，轮对振动加速度随着轮对谐波磨耗幅值的增加而增加。

3.4 包络现象分析

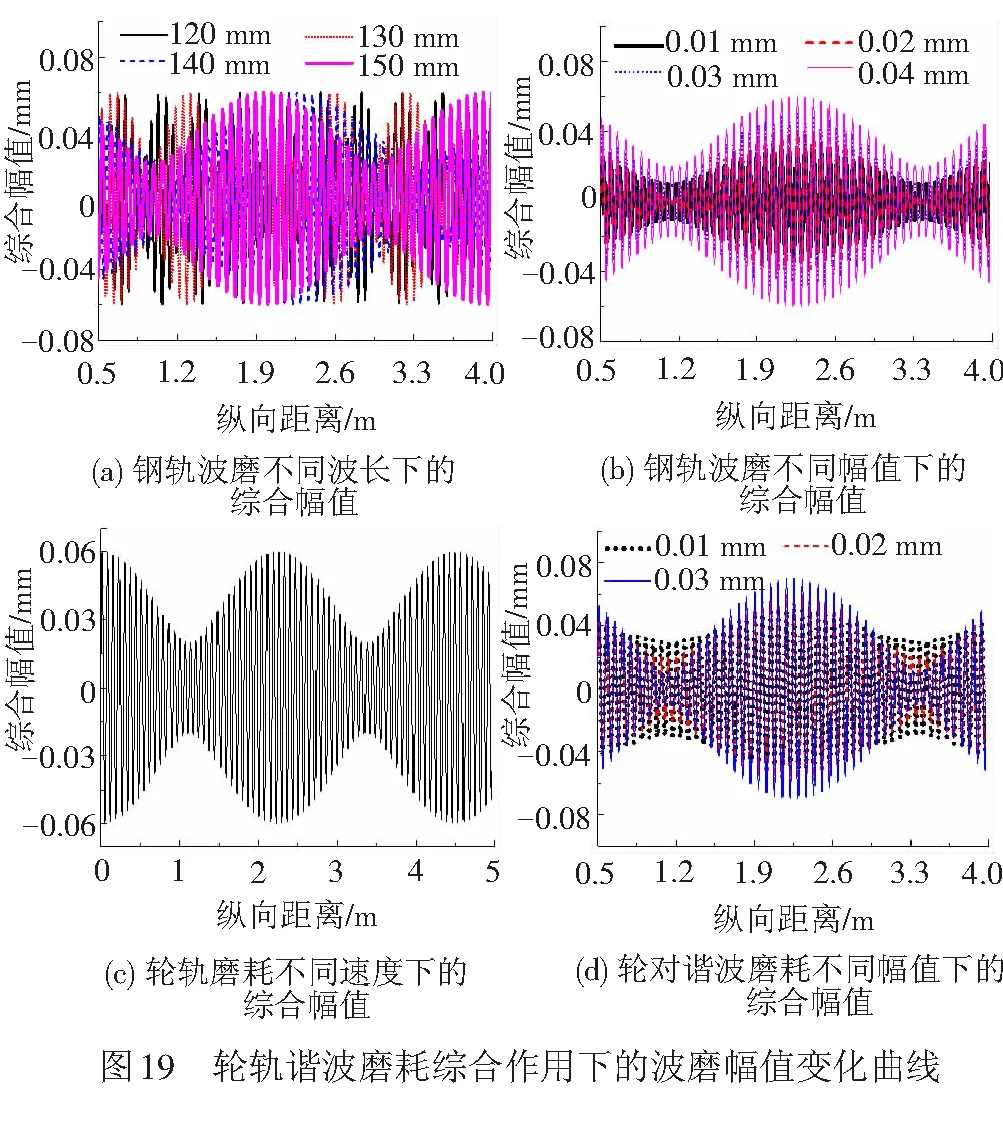
由图15～图18分析可知，轮轨磨耗综合作用下引起的轮对振动加速度呈现出明显的周期性包络现象。为了验证该现象与综合磨耗间的关系，对不同波长及幅值下的轮轨磨耗简谐波进行叠加，见图19。由图19可见，图19(b)、19(d)的包络周期与图16和图18轮对振动加速度的包络周期基本吻合，振动加速度的幅值与叠加谐波包络幅值一致。由图19(a)可以看出，波长越短，包络周期也越短，与图15轮对振动加速度的包络周期吻合，且轮对振动加速度幅值随着叠加谐波包络周期的增大而减小。图19(c)与图17包络周期也基本吻合，振动加速度幅值随着速度的增大而增大。由此可以说明，包络现象是由轮轨谐波磨耗综合作用所致，且振动加速最大值与综合谐波最大幅值一致。造成该现象的主要原因是当轮轨均存在谐波磨耗时，轮对上的谐波磨耗在滚动若干个波长后，其波峰与钢轨磨耗的波谷重合所致。

4 结论

本文利用ANSYS及SIMPACK联合建立了4种轮轨模型，对比分析了不同模型在轮对磨耗、钢轨波磨、轮轨磨耗状态下的振动差异，并分析了柔性轮轨下轮轨磨耗综合作用的振动特性，得到如下结论:

(1) 仿真分析研究时，考虑轮轨均为柔性状态能更真实地反映实际情况下的轮轨耦合振动关系，使仿真分析结果更符合实际，为后续车轮多边形及钢轨波磨机理的深入研究奠定了良好基础。

(2) 轮轨非均匀磨耗综合作用下产生的轮轨垂向力、轮轨振动加速度随着轮轨磨耗幅值的增大而增大，变化与速度、钢轨波磨波长呈非线性关系。且轮轨垂向力、轮对振动加速度在轮轨非均匀磨耗综合作用下呈现出周期性包络现象，与轮轨表面谐波磨耗综合幅值形成的包络周期一致。

(3) 轨道状态相同、单独考虑轮对谐波磨耗时，刚性轮产生的轮轨垂向力大于柔性轮垂向力，因为车速度为300 km/h时，20阶谐波磨耗引起的振动频率远离其垂向共振频率。单独考虑钢轨波磨时，柔性轮产生的轮轨垂向力大于刚性轮垂向力，因为车速度为300 km/h时，140 mm引起的振动频率为595 Hz，激起了轮对的共振。

(4) 轮对状态相同时，柔性轨产生的轮轨垂向力小于刚性轨，因为钢轨垂向共振频率为900 Hz以上，在车速度为300 km/h时，轮轨磨耗引起的振动频率均小于700 Hz，不在钢轨的垂向共振频率范围内。