一种基于低周疲劳特性的含缺陷车轴剩余寿命预测模型

2018-12-13王玉光吴圣川李忠文周平宇马利军

铁道学报 2018年11期

王玉光，吴圣川，李忠文，周平宇，马利军

(1. 中车青岛四方机车车辆股份有限公司技术中心，山东青岛 266111；2. 西南交通大学牵引动力国家重点实验室，四川成都 610031)

截止2015年底，我国铁路营业里程达到12.1万km，其中高铁超过1.9万km，占世界高铁运营总里程的60%以上，是世界上高速铁路发展最快、在建规模最大的国家。列车速度不断提高，运行工况日趋严苛，对转向架关键基础部件的选材、设计、制造、运营和维护提出了迫切要求。

车轴是高速动车组极其重要的安全部件，因此必须确保在线运行车轴状态良好，服役安全可靠，并且充分发挥其使用性能的潜能。然而，车轴在制造、运输、加工、服役和维护中不可避免形成某种缺陷，如磕碰伤、划伤、异物打击或撞击伤以及环境腐蚀和压装部微动疲劳伤损等[1-2]。这些缺陷在旋转弯曲加载作用下，形成疲劳裂纹甚至导致车轴断裂，成为列车运行中的巨大安全隐患。不仅如此，在车轴的设计中也需要对易于形成缺陷的关键部位进行剩余强度和寿命评估，以确保空心车轴服役的安全性、可靠性和经济性[3]。

20世纪工程科学最重大的进步之一是断裂力学的形成、应用与发展。基于断裂力学对含缺陷金属结构进行剩余强度和寿命设计、分析及评估，成功解决了传统名义应力法无法解释和解决的若干重大工程的破坏行为，形成了一系列成熟的缺陷表征和评估技术，这一新型的损伤容限设计思想也相继被国际、国内和地区标准化组织所吸纳[4]。

疲劳裂纹扩展速率是铁路车轴损伤容限设计及寿命评估的关键参数[5-6]。一般通过费时、昂贵的标准小试样和全尺寸试样获得不同应力比下的裂纹扩展速率数据。其中，采用低周疲劳特性和基于裂纹尖端循环应力应变奇异场建立裂纹扩展寿命模型是最具发展前景和应用潜力的一种方法[7]。

车轴属于典型的旋转弯曲部件，关键部位如卸荷槽和压装区应力状态复杂(应力比有正有负，裂纹闭合效应不可忽视)，其中裂纹萌生在总寿命中占据绝大部分，而瞬断区则可忽略不计[8]。为此，论文基于平面应力状态下Ⅰ型裂纹尖端RKE奇异应力应变场，引入裂纹尖端循环塑性区比例加载的应变能失效准则，利用低周疲劳试验能够简单和经济地获取应变控制材料属性的特点，基于改进NASGRO方程，建立了一种新的考虑裂纹闭合效应的裂纹扩展速率模型，并与多种工程结构材料的疲劳裂纹扩展速率数据进行了比较。结果表明，新模型能够模拟不同应力比下的疲劳裂纹扩展行为。

1 材料的循环塑性行为

在远场加载条件下，裂纹前缘形成一个受应变控制的奇异场，损伤的持续累积并最终突破微结构障碍，导致裂纹的稳定扩展。这种局部疲劳是金属材料及结构失效破坏的本质特征，而应力强度因子K是描述裂尖应力场强弱的重要指标。

1.1 裂纹尖端奇异场

众所周知，材料与结构的失效破坏多由局部疲劳引起。在小范围屈服应力条件下，裂纹尖端存在3个区域：疲劳过程区、循环塑性区和单调塑性区，见图1。由于循环加载的作用，裂纹尖端出现钝化，钝化半径ρcp近似于疲劳过程区尺寸。

图1的最外层为单调塑性区，是循环加载中最大拉力载荷影响的边界。中间层为循环塑性区(尺寸为rcp)，它满足比例加载特性，据此可建立起局部循环应力-应变关系。Rice指出Ⅲ型与Ⅰ型裂尖的单调应力和应变场具有相似性[9]，则对于符合单轴Romberg-Osgood本构关系的材料，有

(1)

式中：ε为总应变；σ为总应力；β、n分别为材料应力-应变曲线的拟合参数；σy为单调屈服应力；E为弹性模量；εe、εp分别为弹性和塑形应变。

在平面应力和小屈服条件下，描述Ⅰ型裂纹尖端的循环应力应变场有：Rice-Kujawski-Ellyin(RKE)场和Hutchinson-Rice-Rosengren(HRR)场。研究发现，基于RKE场构建的裂纹扩展速率模型更简单，且不需要过多的人为调整参数。更为主要的是，与HRR场相比，基于RKE场的裂纹扩展速率模型的预测结果更准确和可靠[7,10]。

基于Rice提出的塑形叠加原理和循环塑性区的比例加载特性[11]，得到平面应力条件下幂率硬化材料Ⅰ型裂尖前缘的近似循环RKE场

(2)

式中：r为该点到裂尖的距离；Δεpt、Δσt、n′、K′、εyc和σyc分别为基于低周疲劳行为的循环应变幅值、循环应力幅值、循环应变硬化指数、循环应变硬化系数、循环屈服应变和循环屈服应力；ΔK为线弹性断裂力学描述的应力强度因子幅。

1.2 塑性应变能准则

由式(2)可看出，当研究点接近裂纹尖端(r→∞)时，I型裂纹尖端的循环RKE场表现出奇异性，显然不能基于裂尖材料行为(如临界应力σf或者临界应变εf)来构建疲劳裂纹扩展速率模型。然而实际材料将发生屈服(即形成钝化区)，使得循环塑性区的应变能为有限值[4]。为消除应力奇异性，分别定义钝化区半径和循环塑性区尺寸为

(3)

式中：ΔKth为基于线弹性断裂力学描述的疲劳长裂纹扩展门槛值；ρcp为钝化区尺寸。

则考虑钝化区或疲劳过程区后，循环塑性区内基于RKE场的塑性应变能积分Ecp为

(4)

式中：εy为循环塑性应变。

假设疲劳裂纹以阶跃突进形式在循环塑性区内扩展或失效，则平面应力为零时裂尖塑性区的总扩展抗力Ere可根据材料的低周疲劳Manson-Coffin寿命关系线性累加得到[4]，即

(5)

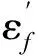
当式(4)中疲劳裂纹尖端循环塑性区中的塑性应变能Ecp与式(5)中的疲劳裂纹扩展抗力Ere相等时，便得到考虑裂尖钝化区后循环塑性区内代表性体积单元上总的失效循环周次

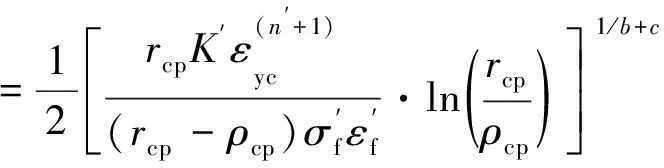
(6)

2 裂纹扩展速率模型

Miner认为裂尖区材料因经受较大的循环应变幅而发生疲劳损伤失效，同时也具有大块金属材料变形时的力学行为。据此，便可在局部低周疲劳与整体疲劳行为之间建立定量关系。结合式(3)、式(6)，得到单位循环周期的裂纹扩展量，即

(7)

由式(7)看出，只要知道了材料或部件的低周疲劳循环属性和应力比下的门槛值，即可得到疲劳裂纹扩展速率曲线。然而，不同应力比下裂纹尖端的循环塑性区以及所需要的循环加载周次显然有较大差别，尤其是当应力比为负值时。

Elber首先发现当拉伸载荷归零之前，上下裂纹面就发生了接触，这就是著名的裂纹闭合效应[12]。新裂纹面的形成必须首先克服塑性尾迹区内的压缩残余应力，抵消掉部分裂纹扩展塑性应变能。根据标准NASGRO模型，式(7)中ΔK在考虑应力比后用等效应力强度因子ΔKeff替换，即有

(8)

式中：R为加载应力比；f为裂纹张开函数[13]。裂纹闭合也对扩展门槛值产生影响，使得短裂纹效应更加突出，甚至导致应力强度因子定义的失效。车轴属于典型的旋转弯曲部件(R<0)，为考虑塑性致裂纹闭合效应[1-2]，提出如下公式

(9)

式中：a为裂纹长度(对于车轴，为深度或半宽度)；aH为E1-Haddad参数(aH=38.1 μm)；ΔKth,0为R=0时的门槛值；ΔKth,R为对应R下的门槛值；f为裂纹张开函数[13];A0为经验常数。即

(10)

式中：

A1=(0.415-0.071α)·(σmax/σyc)

A2=1-A0-A1-A3

A3=2A0+A1-1

(11)

其中，α为与应力状态有关的约束因子；σmax为裂尖最大应力；A1、A2、A3为经验常数。

3 验证与讨论

从式(7)～式(11)可以看出，新提出的寿命模型不仅对门槛区进行了模拟，而且充分考虑了裂纹稳定扩展时的裂纹闭合效应。

为了验证新提出的寿命模型，选取几种典型的工程结构材料，根据其低周疲劳特性和疲劳断裂参数(表1中EA4T钢的低周数据根据狗骨样品的应变疲劳试验获得)，绘制出疲劳裂纹扩展速率曲线，并与相应应力比下的不同比例试样实测的疲劳裂纹扩展数据进行对比分析，见图2～图9。

表1 材料低周疲劳特性及疲劳裂纹扩展门槛值

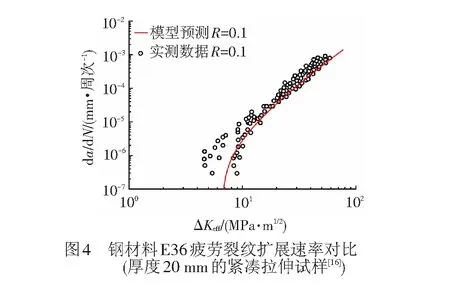
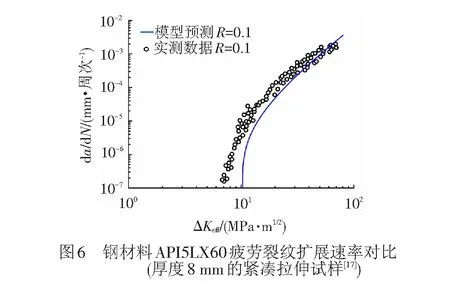
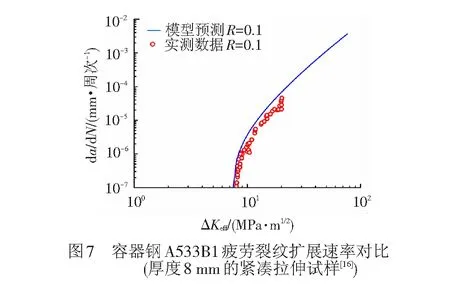
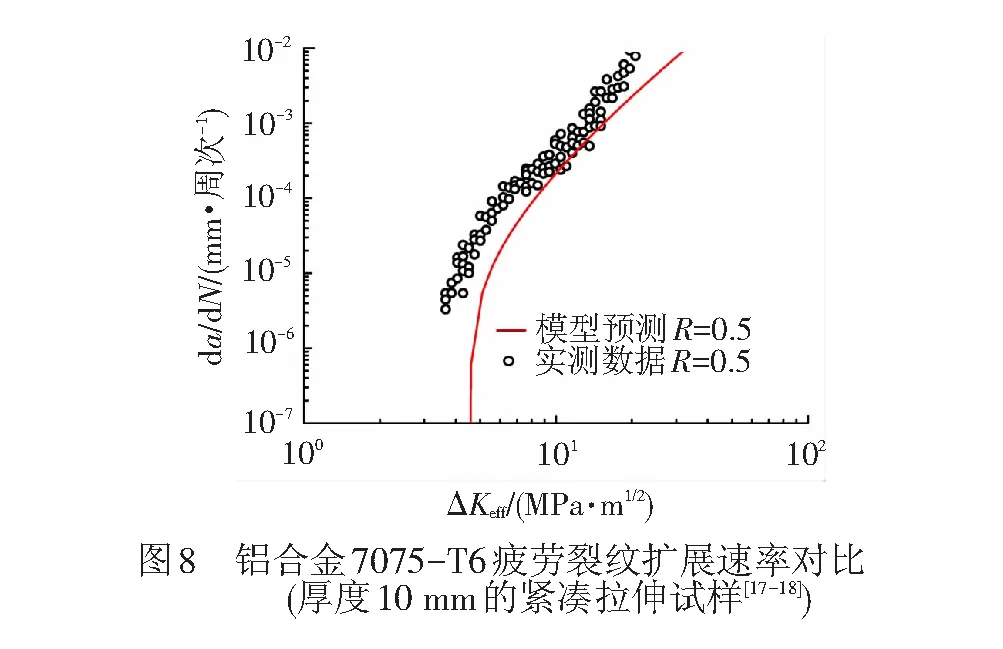
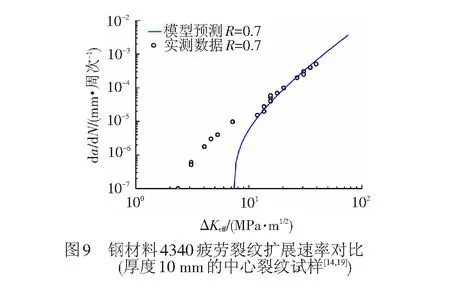
可以清楚地看出，无论是空心车轴专用钢EA4T、常用合金钢，还是轻质高强度的铝合金7075-T6、钛合金Ti-6Al-4V，所提出新裂纹扩展速率模型的理论预测曲线与不同厚度和种类的标准断裂力学试样获得的长裂纹数据吻合较好。此外新模型也可以模拟出近门槛区裂纹扩展行为，一定程度上说明了新提出模型的正确性与可靠性。

2个例外情况是图4中的钢材料E36和图9中的4 340在近门槛区的预测，可从2个方面进行讨论。一是原始数据在近门槛区有较大的分散性符合短裂纹行为的理论解释；二是从理论和试验结果看，短裂纹尖端奇异场的应变能无法保持一个有限值，而能否用长裂纹应力强度因子表征短裂纹行为至今尚无定论[4,13]。

另外需要指出的是，裂纹闭合行为在三维情况下尤其重要和明显，而上述相关数据均是基于标准小试样(平面应力)获得。动车组车轴裂纹扩展特性的深入研究表明，与小尺寸标准试样相比，全尺寸车轴的裂纹扩展速率更低[1-2,20]。而新提出模型的预测值普遍低于小试样实测数据，从另一个角度说明了新模型的可靠性与合理性。

需要指出的是，与类似模型不同的是[21]，本文提出的基于低周疲劳行为的新模型能够预测负应力比(R<0)下的疲劳裂纹扩展速率，同时也对近门槛区短裂纹采用裂纹闭合效应进行了修正，有利于显著降低轴向载荷作用下标准试样裂纹扩展速率测试的费用和难度[5,22]。新模型为我国铁路车轴等典型旋转弯曲部件的损伤容限分析提供了一个重要的剩余寿命模型，而且为研究动车组车轴短裂纹行为及其服役寿命打下坚实的理论基础。

众所周知，不同厚度和种类的标准试样所获得的疲劳裂纹扩展速率也有差别。一般认为，中心裂纹试样预制裂纹尖端的约束更接近于实际裂纹尖端奇异场，所以实测裂纹扩展速率要高于单边裂纹试样和紧凑拉伸试样[23]。但从图2～图9可以看出，新寿命模型也能给出令人满意的预测。

必须指出，对于新模型可靠性与合理性的研究尚需要进一步对比分析，有必要重点加强与标准的NASGRO方程比较，尤其是通过改进新模型，尽可能地模拟出近门槛区短裂纹的贡献。