雷电侵入波下牵引变压器绕组的谐振分析

张友鹏， 王 虹， 张昊磊

(兰州交通大学 自动化与电气工程学院， 甘肃 兰州 730070)

为高速列车供电的高铁牵引变电所，其发生故障将严重威胁高铁行车安全。与普通变电所相比，高铁牵引变电所电压等级高且多建于铁路沿线，钢轨引雷致使变电所遭受雷击的可能性升高[1]。当雷电侵入牵引变电所后，作为核心设备的牵引变压器与所内的其他电气设备相比，过电压值最大，且由于雷电侵入导致的牵引变压器绝缘失效难以修复。因此，应重点研究雷击下牵引变压器的绝缘情况[2]。

雷电侵入波产生的过电压具有较高的峰值及较短的上升时间，且频率变化范围较宽，能造成变压器绕组匝间绝缘击穿[3]。其一，陡度很大的雷电波波头侵入牵引变压器，可能使绕组内部的匝间过电压分布极不均匀，对绕组绝缘危害较大；其二，雷电波频率分布较广，主要频率集中在1 MHz以内，若某几个频率分量与变压器自振频率相吻合，会使绕组产生幅值较高的谐振过电压，可能导致匝间局部绝缘以及绕组与铁芯间的绝缘击穿。

变压器的实际运行情况复杂，对变压器的谐振研究并不完善，鲜有文献对雷电冲击下牵引变压器绕组的谐振情况进行分析。文献[4]对给定变压器的测量数据进行拟合，确定未知参数，最终得到此类变压器谐振频率的一般估算公式。文献[5-6]采用行波理论，将变压器绕组等效为传输线，对变压器各阶谐振频率进行简单估算。但以上2种算法的求解结果精确度较低。而在变压器绕组过电压分析中，绕组多导体传输线(MTLs)模型仿真精度较高且易于编程实现[7-9]，因此本文根据MTLs理论，以匝为单位建立了牵引变压器绕组的单输入多输出端口模型，分析雷电波侵入下谐振对绕组绝缘的影响。

1 基于传输线理论的牵引变压器多端口模型分析

本文根据MTLs理论，搭建牵引变压器绕组以线匝为单位的单输入多输出模型，见图1。分析雷电侵入下，谐振对绕组绝缘的影响。模型中，将绕组等效成多根首尾相连且互相耦合的传输线，Uin及Uout(i)(i=1,2,…,N)分别为输入和输出模型的电压；US,i、IS,i分别为传输线首端的电压、电流；UR,i、IR,i分别为传输线末端的电压、电流。

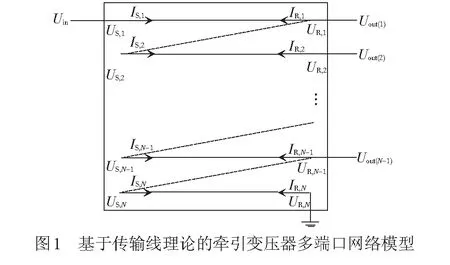
则上述传输线的频域方程[10-12]为

(1)

式中：U(z)为电压矩阵；I(z)为电流矩阵；阻抗矩阵为Z=R+jωL，其中，R为绕组单位长度电阻矩阵，L为电感矩阵；导纳矩阵为Y=G+jωC，其中，G为电导矩阵，C为电容矩阵。

为了求解式(1)，需对上述参数进行求解。

1.1 模型参数求解1.1.1 电容参数求解

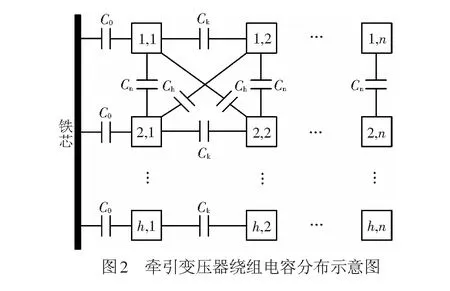
本文涉及的牵引变压器绕组类型为连续式，共有h饼且每饼有n匝，则绕组中各匝间的电容分布情况见图2。实测中发现，绕组的电容参数受频率的影响较小，当频率在100 Hz～1 MHz之间变化时，电容变化量在3%以内[13]。因此，首先忽略频率变化对电容参数的影响，将电容参数做定值处理，在静电场内对其进行求解。本文采用静电场能量公式求解电容参数[14-15]

(2)

式中：Cij为i,j导体间的互电容；Δuij为给导体j施加激励(如U=1 V)后导体i,j之间的电压差；Wj为导体j加激励后的总能量。

本文采用Ansoft有限元软件建模，根据牵引变压器绕组分布规律，考虑计算速度，忽略几何距离较远的绕组之间的互电容计算，仅计算图2的绕组匝间电容Ck、饼间电容Cn、饼间互电容Ch、对地电容C0，利用以上电容参数构造完整的绕组电容矩阵C。在本文后续谐振仿真中，将考虑电容参数增大或减小3%后对牵引变压器绕组谐振的影响。

1.1.2 电阻参数求解

高频条件下导体的集肤效应对导体电阻产生影响，则考虑集肤效应后单位长度电阻矩阵的计算式为

(3)

式中：d1、d2分别为导体横截面的长和宽；f为对应频率；μ为导体材料的磁导率；σ为导体的电导率；E为单位矩阵。

1.1.3 电导参数求解

电导矩阵G是由导体绝缘材料的容性损耗决定的，与频率f、电容矩阵C以及损耗因数tanδ有关，其表达式[16]为

G=2πfCtanδ

(4)

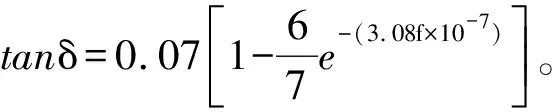
1.1.4 电感参数求解

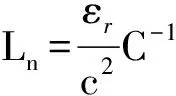
(5)

式中：εr为导体绝缘的相对介电常数；c为真空光速。

1.2 牵引变压器绕组多端口模型求解

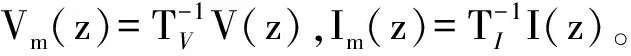
(6)

将式(1)转换为关于模电压、模电流的二阶微分方程式

(7)

求解式(7)并将求解结果变换回原始的电压、电流。已知绕组平均匝长为l，则加入边界条件z=0和z=l，得到绕组多导体传输线模型的始末端电压、电流关系式

(8)

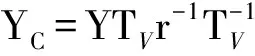
在式(8)中加入牵引变压器绕组的边界条件

式中：N为变压器绕组总匝数。

整理得到

(9)

式中：Yt为经过一系列变换后得到的矩阵。

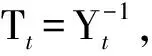
(10)

求解式(10)，得到方程组

(11)

对于实际牵引变压器，最后一匝绕组接地，即UR(N)=0；而US(1)为绕组输入激励，在本文中输入激励为雷电侵入波。则第k(k=2,3,…,N)匝绕组末端电压为

UR(k)=US(k+1)=Tt(k+1,1)IS(1)+

Tt(k+1,N+1)IR(N)

(12)

根据图1所示的牵引变压器多端口模型及式(12)，得到第k(k=1,2,3,…,N)匝绕组末端开路电压传递函数H(k)的表达式为

(13)

1.3 牵引变压器绕组谐振分析

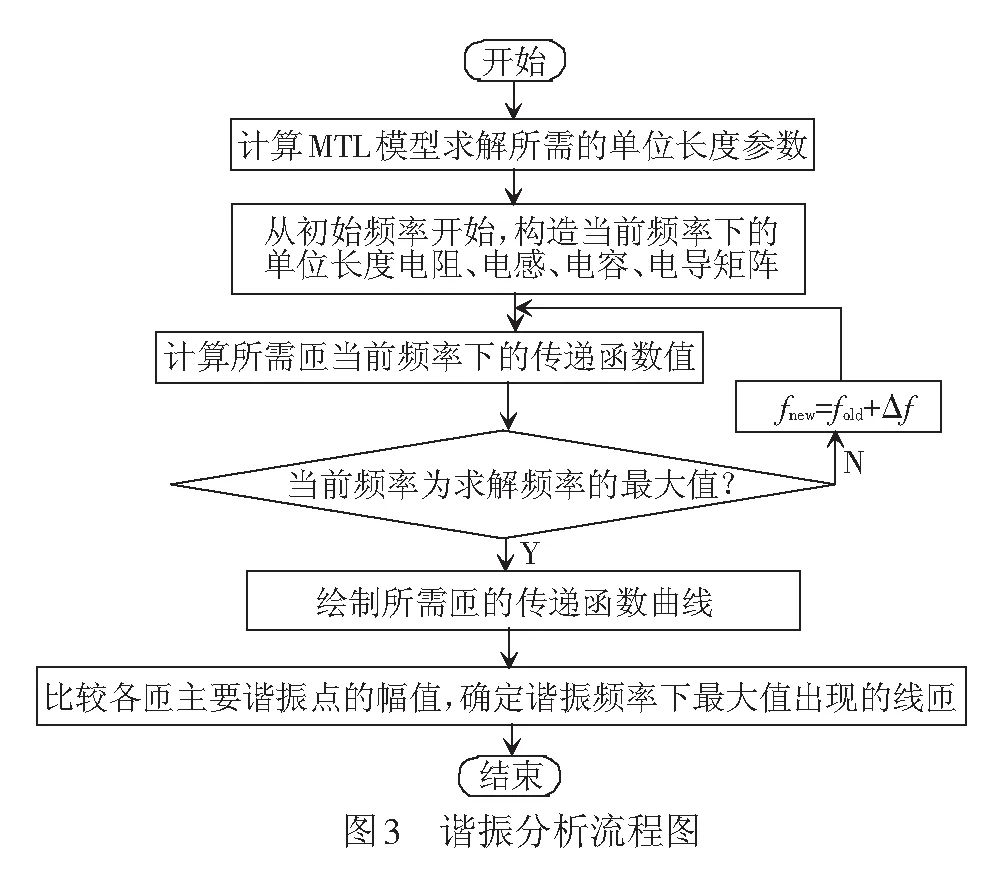
牵引变压器绕组的谐振分析主要是对绕组传递函数的幅频特性进行分析，确定发生谐振的频率并对谐振可能导致的绕组绝缘击穿点进行定位。其具体分析过程见图3。

2 仿真计算及时域验证

2.1 幅频特性分析

根据模型参数求解得到的牵引变压器绕组的基本参数，见表1。

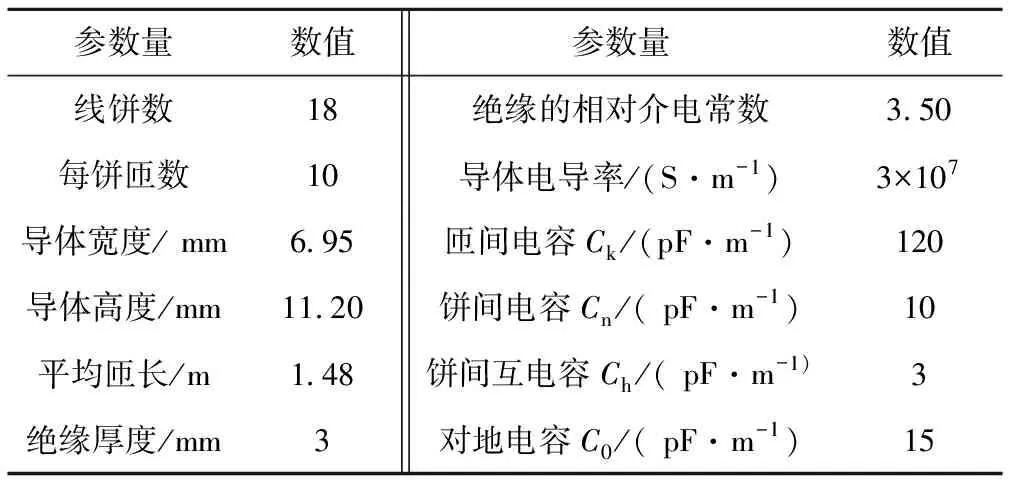
表1 牵引变压器绕组基本参数

在MATLAB中编程，求解得到各匝绕组电压传递函数表达式，仿真得到的第10、20、40、60匝绕组末端的电压传递函数幅频特性曲线，见图4。

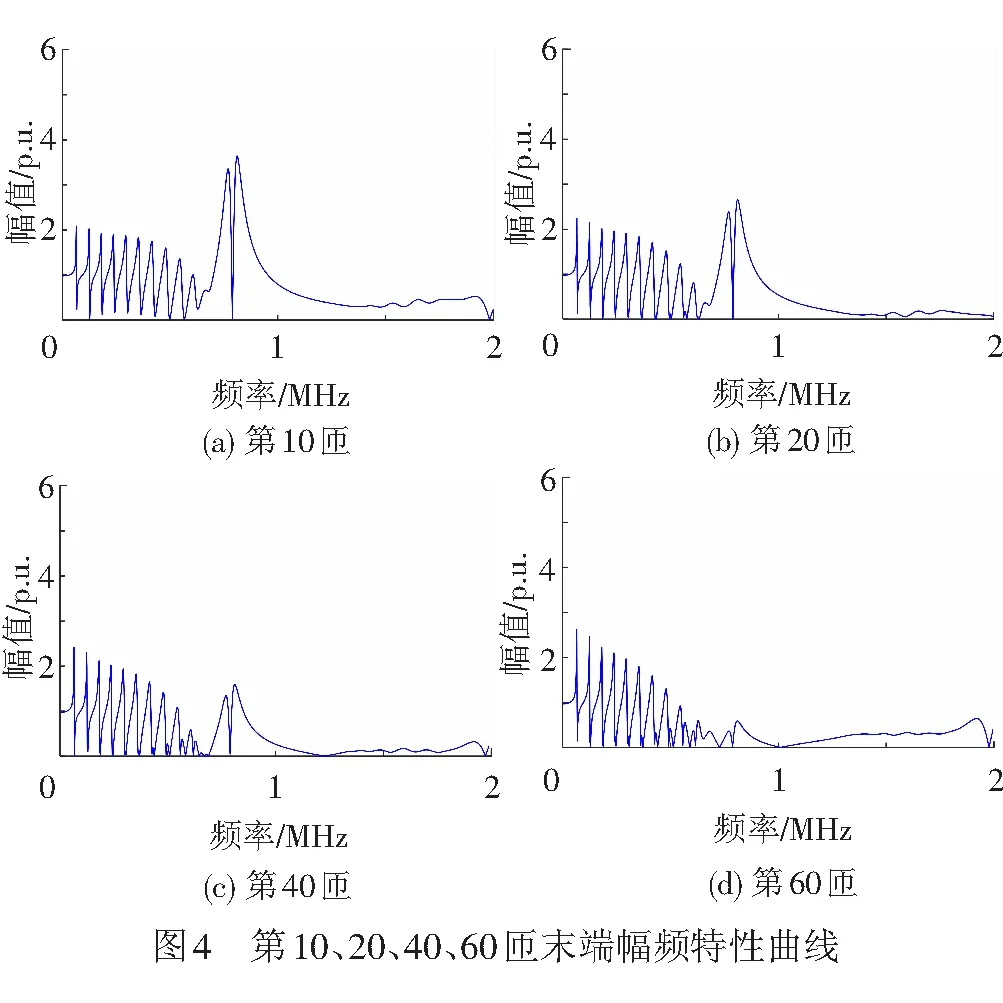
考虑到雷电侵入波本身的特性，即主要频率集中在0 Hz～1 MHz之间，由图4可以看出，牵引变压器绕组的谐振均发生在1 MHz范围内，且靠近绕组首端部分的线匝主要的谐振频率在0.8 MHz左右，随着线匝远离绕组首端，线匝高频分量逐步减弱。这说明雷电侵入波作用下，牵引变压器绕组首端的线匝更易发生绝缘击穿事故。

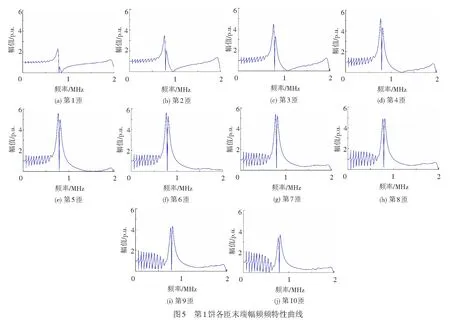
为了详细定位绕组首端因谐振易发生击穿的点，仿真分析第一饼中绕组(前10匝)末端的电压传递函数幅频特性。第一饼绕组线匝末端的电压传递函数幅频特性曲线，见图5。各匝绕组在主要谐振频率附近，幅频特性曲线的最大幅值，见表2。

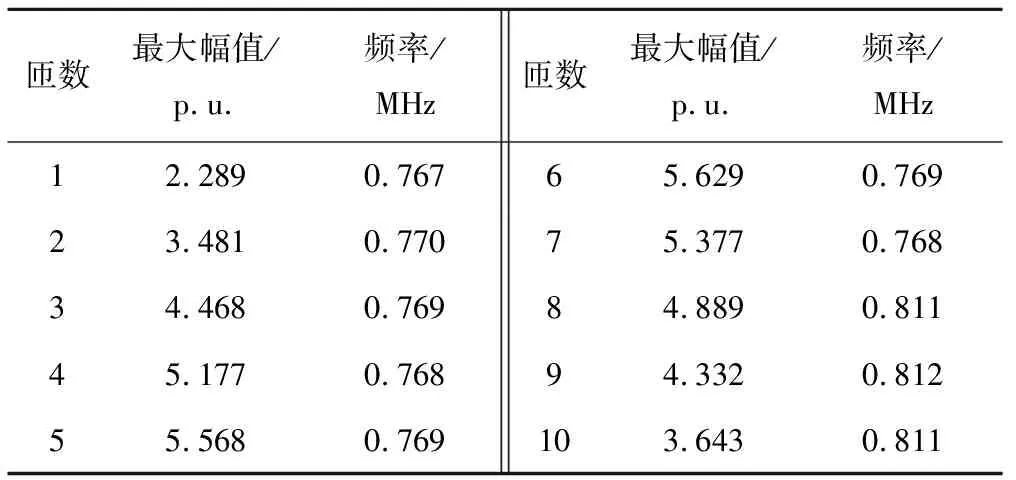
表2 第一饼中各匝绕组幅频特性曲线最大幅值

由图5可以看出，第一饼1～10匝绕组主要谐振频率同上文分析结果相符，其幅频特性曲线最大幅值先呈上升趋势，在5～6匝处达到顶峰后逐次下降。结合表2数据分析可得4～8匝绕组幅频特性曲线最大幅值明显高于其他匝，且5，6匝处幅值最大。这表明雷电入侵时，第一饼线圈中4～8匝绕组绝缘相较其他匝更易因谐振发生击穿，且5，6匝为谐振时绝缘的最薄弱点，在牵引变压器的防雷保护中，应对绝缘相对薄弱的绕组进行重点防护。

2.2 电容参数变化对绕组谐振的影响分析

1.1.1节中提到，当频率在100 Hz～1 MHz之间变化时，牵引变压器绕组电容参数变化量在3%范围内，现考虑最严苛情况下(即电容参数变化量为3%)，绕组谐振的变化情况。本文选取谐振幅值最大的5、6匝绕组进行仿真计算，仿真结果见图6。

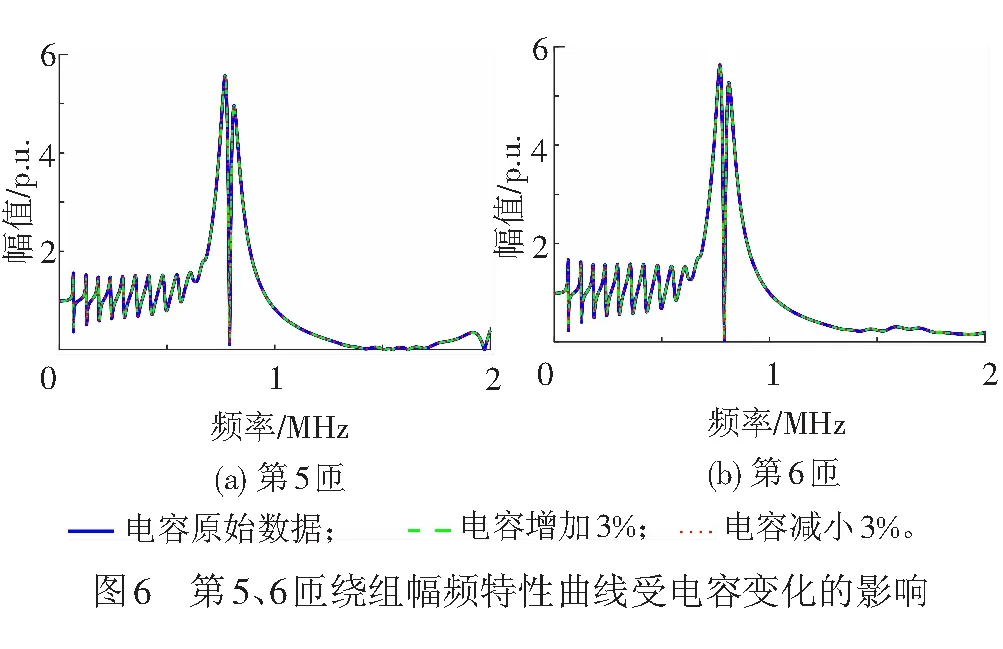
由图6可知，绕组电容参数变化量为3%时，对绕组的幅频特性曲线几乎没有影响。第5、6匝在不同电容参数下的主要谐振频率以及幅频特性曲线最大幅值，见表3。由表3可知，5、6匝的主要谐振频率因电容参数变化而发生的变化基本可以忽略；电容减小3%时，2匝绕组幅频特性曲线最大幅值均有微小的增量，而电容增加3%时，2匝绕组幅频特性曲线最大幅值则微微减小。

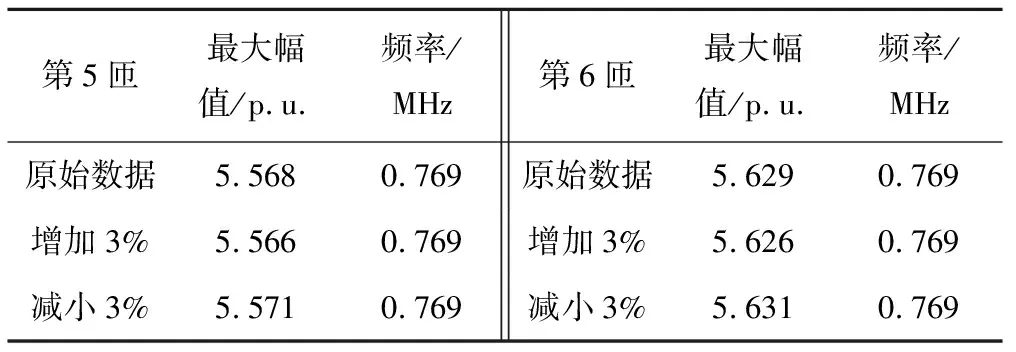
表3 第5、6匝绕组幅频特性曲线最大幅值随电容的变化

综上所述，电容参数极限变化量对绕组谐振的影响十分微弱，可忽略不计，本文将电容参数做定值处理的方法是可行的。

2.3 时域验证

为了验证谐振分析的正确性，在时域内进行验证计算。输入给定幅值200 V的正弦波，频率为主要谐振频率0.769 MHz，对变压器MTL模型进行求解，分析当输入波频率为主要谐振频率时，各匝绕组末端的过电压分布情况，输入波形以及第4～8匝绕组的电压波形见图7，输出电压与输入电压幅值的比值即为对应频率下绕组幅频特性曲线值。由图7可以看出，最大幅值及最大幅值比出现在第5、6匝绕组。

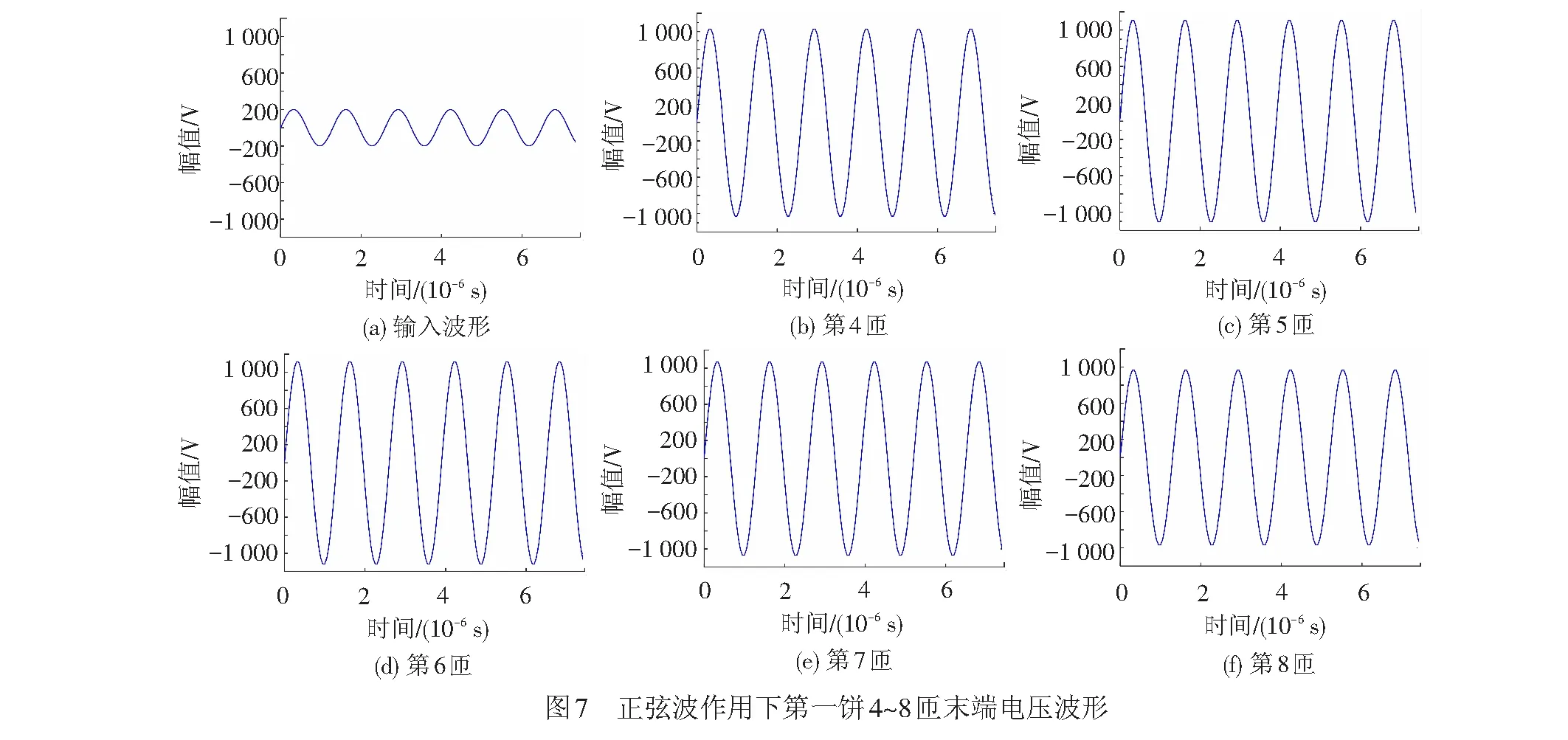
表4 时频结果与谐振分析结果对比

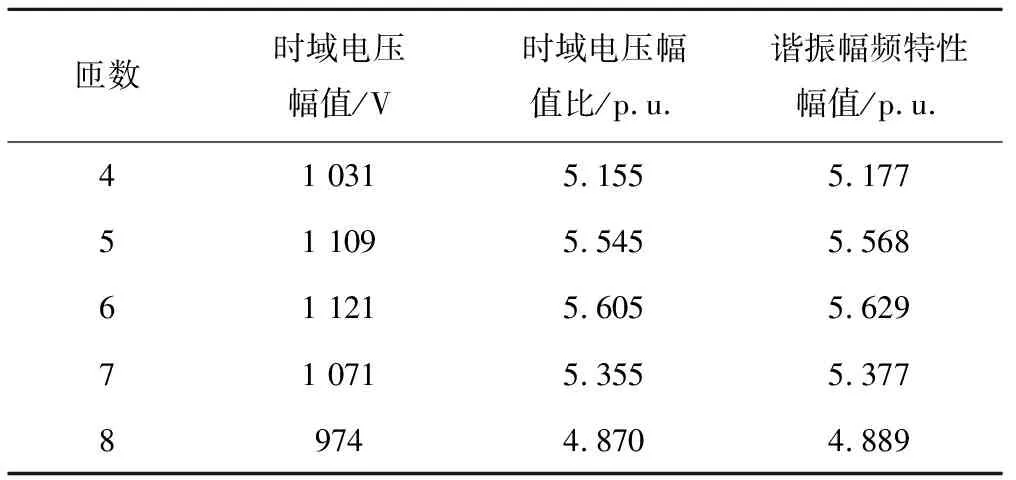
匝数时域电压幅值/V时域电压幅值比/p.u.谐振幅频特性幅值/p.u.41 0315.1555.17751 1095.5455.56861 1215.6055.62971 0715.3555.37789744.8704.889

时域验证与谐振求解的结果对比见表4。由表4可以看出，时域内求解和频域内求解得到的结果相吻合，验证了本文牵引变压器绕组谐振分析的正确性，从而得到结论：分析牵引变压器防雷问题时，应考虑谐振对绕组绝缘的影响，最可能发生绝缘击穿的点为第1饼的5，6匝线圈，应对此进行重点防护。

3 结论

本文根据MTLs理论，搭建牵引变压器绕组以线匝为单位的单输入多输出模型，在该模型下推导出绕组的传递函数表达式，用以分析雷电侵入波下，谐振对绕组绝缘的影响。通过分析传递函数幅频特性，研究绕组中的谐振情况并对谐振可能导致的绕组绝缘击穿点进行定位，分析得到如下结论：第一饼线圈4～8匝绕组绝缘较易因谐振发生击穿，且5、6匝为谐振时绝缘的最薄弱点；通过分析电容参数极限变化情况下对第5、6匝绕组谐振的影响，可知实际运行情况下，电容参数的变化对谐振的影响十分微弱，可以忽略不计，验证了本文将电容参数做定值处理的可行性；在时域内进行验证计算，计算结果符合谐振分析结果，验证了本文方法的可行性与正确性。本方法能够满足实际工程计算需求，为计算雷电侵入下牵引变压器绕组谐振频率及定位可能因谐振发生绝缘击穿的点提供了一种可行的方法，进而为雷电侵入波下牵引变压器的绝缘设计与防护提供了依据。